Article contents
Dynamics of homeomorphisms of the torus homotopic to Dehn twists
Published online by Cambridge University Press: 15 January 2013
Abstract
In this paper, we consider torus homeomorphisms 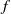 $f$ homotopic to Dehn twists. We prove that if the vertical rotation set of
$f$ homotopic to Dehn twists. We prove that if the vertical rotation set of 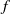 $f$ is reduced to zero, then there exists a compact connected essential ‘horizontal’ set
$f$ is reduced to zero, then there exists a compact connected essential ‘horizontal’ set 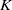 $K$, invariant under
$K$, invariant under  $f$. In other words, if we consider the lift
$f$. In other words, if we consider the lift 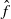 $\hat {f}$ of
$\hat {f}$ of 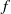 $f$ to the cylinder, which has zero vertical rotation number, then all points have uniformly bounded motion under iterates of
$f$ to the cylinder, which has zero vertical rotation number, then all points have uniformly bounded motion under iterates of 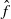 $\hat {f}$. Also, we give a simple explicit condition which, when satisfied, implies that the vertical rotation set contains an interval and thus also implies positive topological entropy. As a corollary of the above results, we prove a version of Boyland’s conjecture to this setting: if
$\hat {f}$. Also, we give a simple explicit condition which, when satisfied, implies that the vertical rotation set contains an interval and thus also implies positive topological entropy. As a corollary of the above results, we prove a version of Boyland’s conjecture to this setting: if 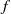 $f$ is area preserving and has a lift
$f$ is area preserving and has a lift 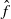 $\hat {f}$ to the cylinder with zero Lebesgue measure vertical rotation number, then either the orbits of all points are uniformly bounded under
$\hat {f}$ to the cylinder with zero Lebesgue measure vertical rotation number, then either the orbits of all points are uniformly bounded under 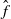 $\hat {f}$, or there are points in the cylinder with positive vertical velocity and others with negative vertical velocity.
$\hat {f}$, or there are points in the cylinder with positive vertical velocity and others with negative vertical velocity.
Information
- Type
- Research Article
- Information
- Copyright
- ©2013 Cambridge University Press
References
- 9
- Cited by

