No CrossRef data available.
Article contents
Entropy estimate by a randomness criterion
Published online by Cambridge University Press: 28 January 2016
Abstract
We propose a new criterion for randomness of a word 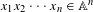 $x_{1}x_{2}\cdots x_{n}\in \mathbb{A}^{n}$ over a finite alphabet
$x_{1}x_{2}\cdots x_{n}\in \mathbb{A}^{n}$ over a finite alphabet 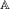 $\mathbb{A}$ defined by
$\mathbb{A}$ defined by 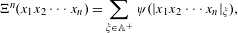 $$\begin{eqnarray}\unicode[STIX]{x1D6EF}^{n}(x_{1}x_{2}\cdots x_{n})=\mathop{\sum }_{\unicode[STIX]{x1D709}\in \mathbb{A}^{+}}\unicode[STIX]{x1D713}(|x_{1}x_{2}\cdots x_{n}|_{\unicode[STIX]{x1D709}}),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EF}^{n}(x_{1}x_{2}\cdots x_{n})=\mathop{\sum }_{\unicode[STIX]{x1D709}\in \mathbb{A}^{+}}\unicode[STIX]{x1D713}(|x_{1}x_{2}\cdots x_{n}|_{\unicode[STIX]{x1D709}}),\end{eqnarray}$$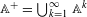 $\mathbb{A}^{+}=\bigcup _{k=1}^{\infty }\mathbb{A}^{k}$ is the set of non-empty finite words over
$\mathbb{A}^{+}=\bigcup _{k=1}^{\infty }\mathbb{A}^{k}$ is the set of non-empty finite words over 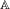 $\mathbb{A}$, for
$\mathbb{A}$, for 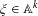 $\unicode[STIX]{x1D709}\in \mathbb{A}^{k}$,
$\unicode[STIX]{x1D709}\in \mathbb{A}^{k}$, 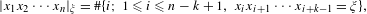 $$\begin{eqnarray}|x_{1}x_{2}\cdots x_{n}|_{\unicode[STIX]{x1D709}}=\#\{i;~1\leq i\leq n-k+1,~x_{i}x_{i+1}\cdots x_{i+k-1}=\unicode[STIX]{x1D709}\},\end{eqnarray}$$
$$\begin{eqnarray}|x_{1}x_{2}\cdots x_{n}|_{\unicode[STIX]{x1D709}}=\#\{i;~1\leq i\leq n-k+1,~x_{i}x_{i+1}\cdots x_{i+k-1}=\unicode[STIX]{x1D709}\},\end{eqnarray}$$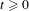 $t\geq 0$,
$t\geq 0$, 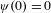 $\unicode[STIX]{x1D713}(0)=0$ and
$\unicode[STIX]{x1D713}(0)=0$ and 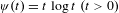 $\unicode[STIX]{x1D713}(t)=t\log t~(t>0)$. This value represents how random the word
$\unicode[STIX]{x1D713}(t)=t\log t~(t>0)$. This value represents how random the word 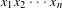 $x_{1}x_{2}\cdots x_{n}$ is from the viewpoint of the block frequency. In fact, we define a randomness criterion as
$x_{1}x_{2}\cdots x_{n}$ is from the viewpoint of the block frequency. In fact, we define a randomness criterion as 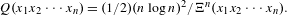 $$\begin{eqnarray}Q(x_{1}x_{2}\cdots x_{n})=(1/2)(n\log n)^{2}/\unicode[STIX]{x1D6EF}^{n}(x_{1}x_{2}\cdots x_{n}).\end{eqnarray}$$
$$\begin{eqnarray}Q(x_{1}x_{2}\cdots x_{n})=(1/2)(n\log n)^{2}/\unicode[STIX]{x1D6EF}^{n}(x_{1}x_{2}\cdots x_{n}).\end{eqnarray}$$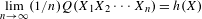 $$\begin{eqnarray}\lim _{n\rightarrow \infty }(1/n)Q(X_{1}X_{2}\cdots X_{n})=h(X)\end{eqnarray}$$
$$\begin{eqnarray}\lim _{n\rightarrow \infty }(1/n)Q(X_{1}X_{2}\cdots X_{n})=h(X)\end{eqnarray}$$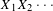 $X_{1}X_{2}\cdots \,$ is an ergodic, stationary process over
$X_{1}X_{2}\cdots \,$ is an ergodic, stationary process over 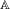 $\mathbb{A}$ either with a finite energy or
$\mathbb{A}$ either with a finite energy or 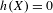 $h(X)=0$, where
$h(X)=0$, where 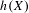 $h(X)$ is the entropy of the process. Another criterion for randomness using
$h(X)$ is the entropy of the process. Another criterion for randomness using 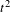 $t^{2}$ instead of
$t^{2}$ instead of 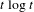 $t\log t$ has already been proposed in Kamae and Xue [An easy criterion for randomness. Sankhya A77(1) (2015), 126–152]. In comparison, our new criterion provides a better fit with the entropy. We also claim that our criterion not only represents the entropy asymptotically but also gives a good representation of the randomness of fixed finite words.
$t\log t$ has already been proposed in Kamae and Xue [An easy criterion for randomness. Sankhya A77(1) (2015), 126–152]. In comparison, our new criterion provides a better fit with the entropy. We also claim that our criterion not only represents the entropy asymptotically but also gives a good representation of the randomness of fixed finite words.
- Type
- Research Article
- Information
- Copyright
- © Cambridge University Press, 2016




