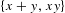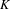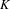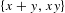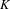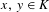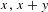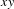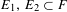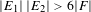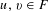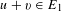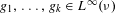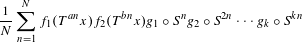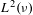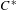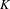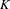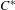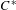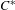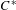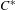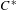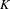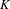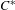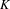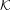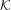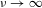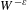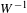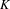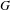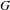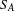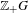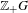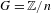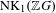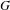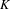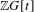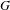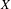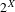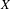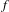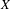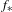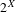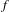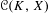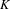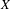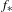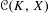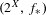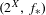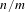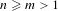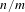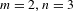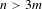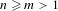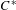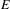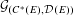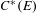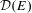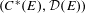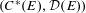Contents
Research Article
Ergodic theorem involving additive and multiplicative groups of a field and
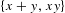 $\{x+y,xy\}$ patterns
$\{x+y,xy\}$ patterns
-
- Published online by Cambridge University Press:
- 06 October 2015, pp. 673-692
-
- Article
- Export citation
A good universal weight for nonconventional ergodic averages in norm
-
- Published online by Cambridge University Press:
- 28 December 2015, pp. 1009-1025
-
- Article
- Export citation
Survey Article
Schrödinger operators with dynamically defined potentials
-
- Published online by Cambridge University Press:
- 11 February 2016, pp. 1681-1764
-
- Article
-
- You have access
- Export citation
Research Article
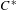 $C^{\ast }$ -algebras of labelled graphs III—
$C^{\ast }$ -algebras of labelled graphs III— 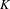 $K$ -theory computations
$K$ -theory computations
-
- Published online by Cambridge University Press:
- 06 October 2015, pp. 337-368
-
- Article
- Export citation
Periodic points and transitivity on dendrites
-
- Published online by Cambridge University Press:
- 08 March 2016, pp. 2017-2033
-
- Article
- Export citation
Asymptotic spectral gap and Weyl law for Ruelle resonances of open partially expanding maps
-
- Published online by Cambridge University Press:
- 07 October 2015, pp. 1-58
-
- Article
- Export citation
On multiple recurrence and other properties of ‘nice’ infinite measure-preserving transformations
-
- Published online by Cambridge University Press:
- 12 February 2016, pp. 1345-1368
-
- Article
- Export citation
Survey Article
Dynamics and spectral theory of quasi-periodic Schrödinger-type operators
-
- Published online by Cambridge University Press:
- 04 July 2016, pp. 2353-2393
-
- Article
- Export citation
Research Article
Conjugacy invariants for Brouwer mapping classes
-
- Published online by Cambridge University Press:
- 08 March 2016, pp. 1765-1814
-
- Article
-
- You have access
- Export citation
On the sum of the non-negative Lyapunov exponents for some cocycles related to the Anderson model
-
- Published online by Cambridge University Press:
- 06 October 2015, pp. 369-388
-
- Article
- Export citation
Finite group extensions of shifts of finite type:
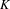 $K$ -theory, Parry and Livšic
$K$ -theory, Parry and Livšic
-
- Published online by Cambridge University Press:
- 11 February 2016, pp. 1026-1059
-
- Article
- Export citation
Return words of linear involutions and fundamental groups
-
- Published online by Cambridge University Press:
- 28 December 2015, pp. 693-715
-
- Article
- Export citation
Symmetric Birkhoff sums in infinite ergodic theory
-
- Published online by Cambridge University Press:
- 04 July 2016, pp. 2394-2416
-
- Article
- Export citation
Non-standard real-analytic realizations of some rotations of the circle
-
- Published online by Cambridge University Press:
- 28 December 2015, pp. 1369-1386
-
- Article
- Export citation
Non-archimedean connected Julia sets with branching
-
- Published online by Cambridge University Press:
- 12 October 2015, pp. 59-78
-
- Article
- Export citation
Dynamics of induced systems
-
- Published online by Cambridge University Press:
- 12 May 2016, pp. 2034-2059
-
- Article
- Export citation
Markov partitions and homology for
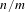 $n/m$ -solenoids
$n/m$ -solenoids
-
- Published online by Cambridge University Press:
- 27 November 2015, pp. 716-738
-
- Article
- Export citation
Statistical properties of the maximal entropy measure for partially hyperbolic attractors
-
- Published online by Cambridge University Press:
- 28 January 2016, pp. 1060-1101
-
- Article
- Export citation
Corrigendum
Non-standard real-analytic realizations of some rotations of the circle – CORRIGENDUM
-
- Published online by Cambridge University Press:
- 19 September 2016, pp. 1387-1388
-
- Article
-
- You have access
- Export citation
Research Article
Graph algebras and orbit equivalence
-
- Published online by Cambridge University Press:
- 25 August 2015, pp. 389-417
-
- Article
- Export citation