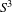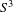Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kegel, Marc
Schneider, Jay
and
Zehmisch, Kai
2020.
Symplectic dynamics and the 3-sphere.
Israel Journal of Mathematics,
Vol. 235,
Issue. 1,
p.
245.
ALBERS, PETER
GEIGES, HANSJÖRG
and
ZEHMISCH, KAI
2022.
Pseudorotations of the -disc and Reeb flows on the -sphere.
Ergodic Theory and Dynamical Systems,
Vol. 42,
Issue. 2,
p.
402.