Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-24T22:55:31.506Z Has data issue: false hasContentIssue false
  • English
  • Français

Optimal state amalgamation is NP-hard

Published online by Cambridge University Press:  07 November 2017

RAFAEL M. FRONGILLO
RAFAEL M. FRONGILLO*
Affiliation:
Department of Computer Science, University of Colorado at Boulder, 1111 Engineering Drive, Boulder, CO 80309-0430, USA email raf@colorado.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

A state amalgamation of a directed graph is a node contraction which is only permitted under certain configurations of incident edges. In symbolic dynamics, state amalgamation and its inverse operation, state splitting, play a fundamental role in the theory of subshifts of finite type (SFT): any conjugacy between SFTs, given as vertex shifts, can be expressed as a sequence of symbol splittings followed by a sequence of symbol amalgamations. It is not known whether determining conjugacy between SFTs is decidable. We focus on conjugacy via amalgamations alone and consider the simpler problem of deciding whether one can perform 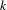$k$ consecutive amalgamations from a given graph. This problem also arises when using symbolic dynamics to study continuous maps, where one seeks to coarsen a Markov partition in order to simplify it. We show that this state amalgamation problem is NP-complete by reduction from the hitting set problem, thus giving further evidence that classifying SFTs up to conjugacy may be undecidable.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 7 , July 2019 , pp. 1857 - 1869
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adler, R.. Symbolic dynamics and Markov partitions. Bull. Amer. Math. Soc. 35(1) (1998), 1–56.Google Scholar
Adler, R. L. and Weiss, B.. Entropy, a complete metric invariant for automorphisms of the torus. Proc. Natl. Acad. Sci. 57(6) (1967), 1573–1576.Google Scholar
Aubrun, N. and Béal, M.-P.. Tree-shifts of finite type. Theoret. Comput. Sci. 459 (2012), 16–25.Google Scholar
Berg, K. R.. On the conjugacy problem for K-systems. PhD Dissertation, University of Minnesota, 1967.Google Scholar
Berger, R.. The Undecidability of the Domino Problem (Memoirs of the American Mathematical Society, 66) . American Mathematical Society, Providence, RI, 1966.Google Scholar
Bowen, R.. Markov partitions for Axiom A diffeomorphisms. Amer. J. Math. 92(3) (1970), 725–747.Google Scholar
Boyle, M.. Open problems in symbolic dynamics. Contemp. Math. 469 (2008), 69–118.Google Scholar
Boyle, M., Kitchens, B. and Marcus, B.. A note on minimal covers for sofic systems. Proc. Amer. Math. Soc. 95(3) (1985), 403–411.Google Scholar
Davis, M. J., MacKay, R. S. and Sannami, A.. Markov shifts in the Hénon family. Physica D 52(2) (1991), 171–178.Google Scholar
Day, S., Frongillo, R. and Trevino, R.. Algorithms for rigorous entropy bounds and symbolic dynamics. SIAM J. Appl. Dyn. Syst. 7(4) (2008), 1477–1506.Google Scholar
Fiebig, D., Fiebig, U.-R. and Jonoska, N.. Multiplicities of covers for sofic shifts. Theoret. Comput. Sci. 262(1–2) (2001), 349–375.Google Scholar
Frongillo, R.. Topological entropy bounds for hyperbolic plateaus of the Henon map. SIAM Undergrad. Res. Online 7 (2014), 142–161.Google Scholar
Goldreich, O.. Computational Complexity: A Conceptual Perspective. Cambridge University Press, Cambridge, 2008.Google Scholar
Hagiwara, R. and Shudo, A.. An algorithm to prune the area-preserving Hénon map. J. Phys. A: Math. Gen. 37(44) (2004), 10521–10543.Google Scholar
Jeandel, E. and Vanier, P.. Hardness of conjugacy, embedding and factorization of multidimensional subshifts. J. Comput. System Sci. 81(8) (2015), 1648–1664.Google Scholar
Johnson, A. and Madden, K.. The decomposition theorem for two-dimensional shifts of finite type. Proc. Amer. Math. Soc. 127(5) (1999), 1533–1543.Google Scholar
Jonoska, N.. Sofic shifts with synchronizing presentations. Theoret. Comput. Sci. 158(1) (1996), 81–115.Google Scholar
Jonoska, N. and Marcus, B.. Minimal presentations for irreducible sofic shifts. IEEE Trans. Inform. Theory 40(6) (1994), 1818–1825.Google Scholar
Kari, J.. Tiling problem and undecidability in cellular automata. Computational Complexity. Springer, New York, 2012, pp. 3198–3211.Google Scholar
Karp, R. M.. Reducibility among combinatorial problems. Complexity of Computer Computations (The IBM Research Symposia Series) . Springer, New York, 1972.Google Scholar
Kim, K. H. and Roush, F. W.. The Williams conjecture is false for irreducible subshifts. Electron. Res. Announc. Amer. Math. Soc. 3 (1997), 105–109.Google Scholar
Kim, K. H. and Roush, F. W.. Decidability of shift equivalence. Dynamical Systems. Springer, New York, 1988, pp. 374–424.Google Scholar
Kitchens, B.. Symbolic Dynamics: One-Sided, Two-Sided and Countable State Markov Shifts. Springer, New York, 1998.Google Scholar
Lind, D. and Marcus, B.. An Introduction to Symbolic Dynamics and Coding. Cambridge University Press, Cambridge, 1999.Google Scholar
Schmidt, K.. Multi-dimensional symbolic dynamical systems. Codes, Systems, and Graphical Models. Springer, New York, 2001, pp. 67–82.Google Scholar
Sinai, Y. G.. Markov partitions and C-diffeomorphisms. Funct. Anal. Appl. 2(1) (1968), 61–82.Google Scholar
Sinai, Y. G.. Construction of Markov partitions. Funct. Anal. Appl. 2(3) (1968), 245–253.Google Scholar
Teramoto, H. and Komatsuzaki, T.. How does a choice of Markov partition affect the resultant symbolic dynamics? Chaos 20(3) (2010), 037113.Google Scholar
Trow, P.. Determining presentations of sofic shifts. Theoret. Comput. Sci. 259(1) (2001), 199–216.Google Scholar
Williams, R. F.. Classification of one dimensional attractors. Global Analysis (Proceedings of Symposia in Pure Mathematics, XIV, Berkeley, CA, 1968). Providence, RI, 1970, pp. 341–361.Google Scholar
Williams, R. F.. Classification of subshifts of finite type. Ann. of Math. (2) 98(1) (1973), 120–153.Google Scholar
Zheng, J., Skufca, J. D. and Bollt, E. M.. Comparing dynamical systems by a graph matching method. Physica D 255 (2013), 12–21.Google Scholar