Hostname: page-component-7479d7b7d-fwgfc Total loading time: 0 Render date: 2024-07-13T04:54:03.262Z Has data issue: false hasContentIssue false
  • English
  • Français

Regularity at infinity of compact negatively curved manifolds

Published online by Cambridge University Press:  19 September 2008

Ursula Hamenstädt
Ursula Hamenstädt
Affiliation:
Mathematisches Institut der Universität Bonn, Beringstrasse 1, 5300 Bonn, Germany
Get access Rights & Permissions [Opens in a new window]

Abstract

It is shown that three different notions of regularity for the stable foliation on the unit tangent bundle of a compact manifold of negative curvature are equivalent. Moreover if 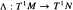is a time-preserving conjugacy of geodesic flows of such manifolds M, N then the Lyapunov exponents at corresponding periodic points of the flows coincide. In particular Δ also preserves the Lebesgue measure class.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 14 , Issue 3 , September 1994 , pp. 493 - 514
Copyright
Copyright © Cambridge University Press 1994

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[B-F-L]Benoist, Y., Foulon, P. and Labourie, F.. Flots d'Anosov à distributions stable et instable diffèrentiables. Journal Amer. Math. Soc. 4 (1992), 33–74.Google Scholar
[C]Croke, C.. Rigidity for surfaces of non-positive curvature. Commun. Math. Helv. 65 (1990), 150–169.CrossRefGoogle Scholar
[F-O]Feldman, J. and Ornstein, D.. Semi-rigidity of horocycle flows over surfaces of variable negative curvature. Ergod. Th. & Dynam. Sys. 7 (1987), 49–72.CrossRefGoogle Scholar
[Gh]Ghys, E.. Flots d'Anosov dont des feuilletages stables sont diffèrentiables. Ann. Ecole Normale Sup. 20(1987), 251–270.CrossRefGoogle Scholar
[G]Gromov, M.. Three remarks on geodesic dynamics and fundamental group. Unpublished note.Google Scholar
[HI]Hamenstädt, U.. Time preserving conjugacies of geodesic flows. Ergod. Th. & Dynam. Sys. 12 (1992), 67–74.Google Scholar
[H2]Hamenstädt, U.. Regularity of time-preserving conjugacies for contact Anosov flows with C 1-Anosov splitting. Ergod. Th. & Dynam. Sys. 13 (1993), 65–72.Google Scholar
[H3]Hamenstädt, U.. A geometric characterization of negatively curved locally symmetric spaces. J. Diff. Geom. 34 (1991), 193–221.Google Scholar
[Hs]Hasselblatt, B.. Regularity of the Anosov splitting and horospheric foliations. Ergod. Th. & Dynam. Sys. To appear.Google Scholar
[H-JH]Heintze, E. and Hof, H.C. Im. Geometry of horospheres. J. Diff. Geom. 12 (1977), 481–491.Google Scholar
[H-P]Hirsch, M. and Pugh, C.. Smoothness of horocycle foliations. J. Dig. Geom. 10 (1975), 225–238.Google Scholar
[H-K]Hurder, S. and Katok, A.. Differentiability, rigidity and Godbillon—Vey classes for Anosov flows. Publ. IHES 72 (1990), 5–61.Google Scholar
[Kn1]Kanai, M.. Geodesic flows of negatively curved manifolds with smooth stable and unstable foliations. Ergod. Th. & Dynam. Sys. 8 (1988), 215–240.CrossRefGoogle Scholar
[kN2]Kanai, M.. Differential geometric studies on dynamics of geodesic and frame flows. Jap. J. Math. 19 (1993), 1–30.CrossRefGoogle Scholar
[K]Katok, A.. Entropy and closed geodesies. Ergod. Th. & Dynam. Sys. 2 (1982), 339–366.CrossRefGoogle Scholar
[Kl]Klingenberg, W.. Riemannian Geometry, de Gruyter: Berlin, 1982.Google Scholar
[L-Y]Ledrappier, F. and Young, L.S.. The metric entropy of diffeomorphisms. Ann. Math. 122 (1985), 509–539.Google Scholar
[L-M-M]Llave, R. de la, Marco, J. and Moriyon, R.. Canonical perturbation theory of Anosov systems and regularity results for Livsic cohomology equation. Ann. Math. 123 (1986), 537–612.CrossRefGoogle Scholar
[O1]Otal, J.P.. Le spectre marqué des longeurs des surfaces à courbure négative. Ann. Math. 131 (1990), 151–162.CrossRefGoogle Scholar
[O2]Otal, J.P.. Sur la géometrie symplectique de l'espace desgéodésiques d'une variété a courbure négative. Rev. Mat. Jberoam. 8 (1992), 441–456.Google Scholar
[Sh]Shub, M.. Global Stability of Dynamical Systems. Springer: Berlin, 1987CrossRefGoogle Scholar