Hostname: page-component-77c89778f8-7drxs Total loading time: 0 Render date: 2024-07-23T18:20:16.575Z Has data issue: false hasContentIssue false
  • English
  • Français

Subdiagrams and invariant measures on Bratteli diagrams

Published online by Cambridge University Press:  12 May 2016

M. ADAMSKA ,
S. BEZUGLYI ,
O. KARPEL  and
J. KWIATKOWSKI
M. ADAMSKA
Affiliation:
The University of Warmia and Mazury, Olsztyn, Poland email malwina.adamska@gmail.com
S. BEZUGLYI
Affiliation:
Department of Mathematics, Institute for Low Temperature Physics, Kharkiv, Ukraine email bezuglyi@gmail.com, helen.karpel@gmail.com Department of Mathematics, University of Iowa, Iowa City, 52242 IA, USA
O. KARPEL
Affiliation:
Department of Mathematics, Institute for Low Temperature Physics, Kharkiv, Ukraine email bezuglyi@gmail.com, helen.karpel@gmail.com Department of Dynamical Systems, Institute of Mathematics of the Polish Academy of Sciences, Warsaw, Poland
J. KWIATKOWSKI
Affiliation:
Kotarbinski University of Information Technology and Management, Olsztyn, Poland email jkwiat@mat.umk.pl
Get access Rights & Permissions [Opens in a new window]

Abstract

We study ergodic finite and infinite measures defined on the path space 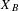$X_{B}$ of a Bratteli diagram 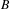$B$ which are invariant with respect to the tail equivalence relation on 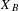$X_{B}$. Our interest is focused on measures supported by vertex and edge subdiagrams of 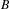$B$. We give several criteria when a finite invariant measure defined on the path space of a subdiagram of 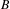$B$ extends to a finite invariant measure on 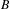$B$. Given a finite ergodic measure on a Bratteli diagram 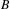$B$ and a subdiagram 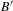$B^{\prime }$ of 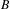$B$, we find the necessary and sufficient conditions under which the measure of the path space 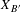$X_{B^{\prime }}$ of $B^{\prime }$ is positive. For a class of Bratteli diagrams of finite rank, we determine when they have maximal possible number of ergodic invariant measures. The case of diagrams of rank two is completely studied. We also include an example which explicitly illustrates the proven results.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 37 , Issue 8 , December 2017 , pp. 2417 - 2452
Copyright
© Cambridge University Press, 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bezuglyi, S. and Karpel, O.. Homeomorphic measures on stationary Bratteli diagrams. J. Funct. Anal. 261 (2011), 3519–3548.CrossRefGoogle Scholar
Bezuglyi, S., Karpel, O. and Kwiatkowski, J.. Subdiagrams of Bratteli diagrams supporting finite invariant measures. J. Math. Phys. Anal. Geom. 11 (2015), 3–17.Google Scholar
Bezuglyi, S., Kwiatkowski, J., Medynets, K. and Solomyak, B.. Invariant measures on stationary Bratteli diagrams. Ergod. Th. & Dynam. Sys. 30 (2013), 973–1007.Google Scholar
Bezuglyi, S., Kwiatkowski, J., Medynets, K. and Solomyak, B.. Finite rank Bratteli diagrams: structure of invariant measures. Trans. Amer. Math. Soc. 365 (2013), 2637–2679.Google Scholar
Bezuglyi, S., Kwiatkowski, J. and Yassawi, R.. Perfect orderings on finite rank Bratteli diagrams. Canad. J. Math. 66 (2014), 57–101.Google Scholar
Bratteli, O.. Inductive limits of finite-dimensional C ∗ -algebras. Trans. Amer. Math. Soc. 171 (1972), 195–234.Google Scholar
Bezuglyi, S. and Yassawi, R.. Orders that yield homeomorphisms on Bratteli diagrams. Preprint, 2013.Google Scholar
Durand, F.. Combinatorics on Bratteli diagrams and dynamical systems. Combinatorics, Automata and Number Theory (Encyclopedia of Mathematics and its Applications, 135) . Eds. Berthé, V. and Rigo, M.. Cambridge University Press, Cambridge, 2010, pp. 338–386.Google Scholar
Grillenberger, C.. Constructions of strictly ergodic systems. I. Given entropy. Z. Wahrscheinlichkeitstheor. Verwandte Geb. 25 (1972/73), 323–334.Google Scholar
Gantmacher, F. R.. The Theory of Matrices, Matrix Theory. AMS Chelsea Publishing, Providence, RI, 1998, p. 660.Google Scholar
Gjerde, R. and Johansen, O.. Bratteli–Vershik models for Cantor minimal systems: applications to Toeplitz flows. Ergod. Th. & Dynam. Sys. 20 (2000), 1687–1710.Google Scholar
Giordano, T., Putnam, I. and Skau, C.. Topological orbit equivalence and C ∗ -crossed products. J. Reine Angew. Math. 469 (1995), 51–111.Google Scholar
Giordano, T., Putnam, I. and Skau, C.. Affable equivalence relations and orbit structure of Cantor dynamical systems. Ergod. Th. & Dynam. Sys. 24 (2004), 441–475.Google Scholar
Handelman, D.. Equal column sum and equal row sum dimension group realizations. Preprint, 2013, arXiv:1301.2799.Google Scholar
Herman, R. H., Putnam, I. and Skau, C.. Ordered Bratteli diagrams, dimension groups, and topological dynamics. Int. J. Math. 3(6) (1992), 827–864.CrossRefGoogle Scholar
Medynets, K.. Cantor aperiodic systems and Bratteli diagrams. C. R. Math. Acad. Sci. Paris 342(1) (2006), 43–46.Google Scholar
Pullman, N. J.. A geometric approach to the theory of nonnegative matrices. Linear Algebra Appl. 4 (1971), 827–864.Google Scholar
Phelps, R. R.. Lectures on Choquet’s Theorem. Springer, Heidelberg, 2001.CrossRefGoogle Scholar
Vershik, A.. Uniform algebraic approximation of shift and multiplication operators. Dokl. Akad. Nauk 259 (1981), 526–529 (in Russian).Google Scholar