Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Arnoux, Pierre
Ornstein, Donald S.
and
Weiss, Benjamin
1985.
Cutting and stacking, interval exchanges and geometric models.
Israel Journal of Mathematics,
Vol. 50,
Issue. 1-2,
p.
160.
Parry, William
1987.
The New Palgrave Dictionary of Economics.
p.
1.
Parry, William
1990.
Time Series and Statistics.
p.
73.
Meyerovitch, Tom
2011.
Quasi-factors and relative entropy for infinite-measure-preserving transformations.
Israel Journal of Mathematics,
Vol. 185,
Issue. 1,
p.
43.
BABICHEV, ANDREY
BURTON, ROBERT M.
and
FIELDSTEEL, ADAM
2013.
Speedups of ergodic group extensions.
Ergodic Theory and Dynamical Systems,
Vol. 33,
Issue. 4,
p.
969.
Parry, William
2018.
The New Palgrave Dictionary of Economics.
p.
3878.

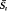 ,
, 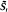
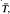 ,
, 