Hostname: page-component-77c89778f8-sh8wx Total loading time: 0 Render date: 2024-07-23T09:33:18.077Z Has data issue: false hasContentIssue false
  • English
  • Français

The Connes spectrum for actions of Abelian groups on continuous-trace algebras

Published online by Cambridge University Press:  19 September 2008

Steven Hurder ,
Dorte Olesen ,
Iain Raeburn  and
Jonathan Rosenberg
Steven Hurder
Affiliation:
Department of Mathematics, University of Illinois at Chicago, P.O. Box 4348, Chicago, Illinois 60680, USA;
Dorte Olesen
Affiliation:
Matematisk Institut, Universitetsparken 5, 2100 København Ø, Denmark;
Iain Raeburn
Affiliation:
School of Mathematics, University of New South Wales, P.O. Box 1, Kensington, NSW 2033, Australia;
Jonathan Rosenberg
Affiliation:
Department of Mathematics, University of Maryland, College Park, Maryland 20742, USA
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the various notions of spectrum for an action α of a locally compact abelian group G on a type IC*-algebra A, and discuss how these are related to the structure of the crossed product A ⋊αG. In the case where A has continuous trace and the action of G on  is minimal, we completely describe the ideal structure of the crossed product. A key role is played by the restriction of α to a certain ‘symmetrizer subgroup’ S of the common stabilizer in G of the points of Â. We show by example that, contrary to a conjecture of Bratteli, it is possble for A⋊G to be primitive but not simple, provided that S is not discrete. In such cases, the Connes spectrum Γ(α) differs from the strong Connes spectrum 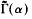of Kishimoto. The counterexamples come from subtle phenomena in topological dynamics.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 6 , Issue 4 , December 1986 , pp. 541 - 560
Copyright
Copyright © Cambridge University Press 1986

References

REFERENCES

[AM]Auslander, L. & Moore, C. C.. Unitary Representations of Solvable Lie Groups. Mem. Amer. Math. Soc., no. 62 (1966).Google Scholar
[BK]Baggett, L. & Kleppner, A.. Multiplier representations of abelian groups. J. Fund. Anal. 14 (1973), 299–324.CrossRefGoogle Scholar
[Br]Bratteli, O.. Crossed products of UHF algebras by product type actions. Duke. Math. J. 46 (1979), 1–23.CrossRefGoogle Scholar
[Eb1]Eberlein, P.. Geodesic flow in certain manifolds without conjugate points. Trans. Amer. Math. Soc. 167 (1972), 151–170.CrossRefGoogle Scholar
[Eb2]Eberlein, P.. Horocycle flows on certain surfaces without conjugate points. Trans. Amer. Math. Soc. 233 (1977), 1–36.CrossRefGoogle Scholar
[ET]Evans, D. E. & Takai, H.. Simplicity of crossed products of GCR algebras by abelian groups. Math. Ann. 243 (1979), 55–62.CrossRefGoogle Scholar
[Goot1]Gootman, E. C.. On certain properties of crossed products. Proc. Symp. Pure Math. (Amer. Math. Soc.) 38 (1982), Part I, 311–322.CrossRefGoogle Scholar
[Goot2]Gootman, E. C.. Abelian group actions on Type I C*-algebras. Preprint, University of Georgia.CrossRefGoogle Scholar
[GO]Gootman, E. C. & Olesen, D.. Spectra of actions on type I C*-algebras. Math. Scand. 47 (1980), 329–349.CrossRefGoogle Scholar
[GR]Gootman, E. C. & Rosenberg, J.. The structure of crossed product C*-algebras: a proof of the generalized Effros-Hahn conjecture. Invent. Math. 52 (1979), 283–298.CrossRefGoogle Scholar
[Gr1]Green, P.. C*-algebras of transformation groups with smooth orbit space. Pacific J. Math. 72 (1977), 71–97.CrossRefGoogle Scholar
[Gr2]Green, P.. The local structure of twisted covariance algebras. Acta Math. 140 (1978), 191–250.CrossRefGoogle Scholar
[H]Herman, M. R.. Construction d'un difféomorphisme minimale d'entropie topologique non nulle. Ergod. The. Dynam. Sys. 1 (1981), 65–76.CrossRefGoogle Scholar
[Ki]Kishimoto, A.. Simple crossed products of C* -algebras by locally compact abelian groups. Yokohama Math. J. 38 (1980), 69–85.Google Scholar
[KB]Kryloff, N. & Bogoliouboff, N.. La théorie générale de la mesure dans son application 'étude des systèmes dynamiques de la méchanique nonlinéare. Annals of Math. 38 (1937), 65–113.CrossRefGoogle Scholar
[La]Lance, E. C.. Automorphisms of postliminal C* -algebras. Pacific J. Math. 23 (1967), 547–555.CrossRefGoogle Scholar
[LOP]Landstad, M. B., Olesen, D. & Pedersen, G. K.. Towards a Galois theory for C* -crossed products. Math. Scand. 43 (1978), 311–321.CrossRefGoogle Scholar
[M]Moore, C. C.. Group extensions and cohomology for locally compact groups, III, Trans. Amer. Math. Soc. 221 (1976), 1–33.CrossRefGoogle Scholar
[Ol]Olesen, D.. A classification of ideals in crossed products. Math. Scand. 45 (1979), 157–167.CrossRefGoogle Scholar
[OP1]Olesen, D. & Pedersen, G. K.. Applications of the Connes spectrum to C*-dynamical systems. J. Fund. Anal. 30 (1978), 179–197.CrossRefGoogle Scholar
[OP2]Olesen, D. & Pedersen, G. K.. Applications of the Connes spectrum to C*-dynamical systems, II, J. Funct. Anal. 36 (1980), 18–32.CrossRefGoogle Scholar
[OP3]Olesen, D. & Pedersen, G. K.. Applications of the Connes spectrum to C*-dynamical systems, III. J. Funct. Anal. 45 (1982), 357–390.CrossRefGoogle Scholar
[P1]Pedersen, G. K.. C*-algebras and their Automorphism Groups. London Math. Soc. Monographs Vol. 14. Academic Press, London, 1979.Google Scholar
[P2]Pedersen, G. K.. Dynamical systems and crossed products. Proc. Symp. Pure Math. (Amer. Math. Soc.) 38 (1982), Part I, 271–283.Google Scholar
[PR1]Phillips, J. & Raeburn, I.. Automorphisms of C* -algebras and second Čech cohomology. Indiana Univ. Math. J. 29 (1980), 799–822.CrossRefGoogle Scholar
[PR2]Phillips, J. & Raeburn, I.. Crossed products by locally unitary automorphism groups and principal bundles. J. Operator Th. 11 (1984), 215–241.Google Scholar
[RR]Raeburn, I. & Rosenberg, J.. Crossed products of continuous–trace C* -algebras by smooth actions. Preprint MSRI, 1985, No. 05711–85.Google Scholar
[R]Rosenberg, J.. Some results on cohomology with Borel cochains, with applications to group actions on operator algebras. Preprint MSRI, 1985, No. 03611–85.Google Scholar
[Wi]Williams, D. P.. The topology on the primitive ideal space of transformation group C* -algebras and CCR transformation group C* -algebras. Trans. Amer. Math. Soc. 266 (1981), 335–359.Google Scholar
[Wr]Wright, F. B.. Semigroups in compact groups. Proc. Amer. Math. Soc. 7 (1956), 309–311.CrossRefGoogle Scholar