No CrossRef data available.
Article contents
Entropy bounds for multi-word perturbations of subshifts
Part of:
Topological dynamics
Published online by Cambridge University Press: 27 March 2023
Abstract
Given a subshift 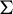 $\Sigma $ of finite type and a finite set S of finite words, let
$\Sigma $ of finite type and a finite set S of finite words, let 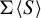 $\Sigma \langle S\rangle $ denote the subshift of
$\Sigma \langle S\rangle $ denote the subshift of 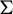 $\Sigma $ that avoids S. We establish a general criterion under which we can bound the entropy perturbation
$\Sigma $ that avoids S. We establish a general criterion under which we can bound the entropy perturbation 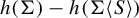 $h(\Sigma ) - h(\Sigma \langle S\rangle )$ from above. As an application, we prove that this entropy difference tends to zero with a sequence of such sets
$h(\Sigma ) - h(\Sigma \langle S\rangle )$ from above. As an application, we prove that this entropy difference tends to zero with a sequence of such sets 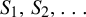 $S_1, S_2,\ldots $ under various assumptions on the
$S_1, S_2,\ldots $ under various assumptions on the 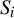 $S_i$.
$S_i$.
MSC classification
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
Guibas, L. J. and Odlyzko, A. M.. Maximal prefix-synchronized codes. SIAM J. Appl. Math. 35(2) (1978), 401–418.10.1137/0135034CrossRefGoogle Scholar
Guibas, L. J. and Odlyzko, A. M.. String overlaps, pattern matching, and nontransitive games. J. Combin. Theory Ser. A 30(2) (1981), 183–208.10.1016/0097-3165(81)90005-4CrossRefGoogle Scholar
Guibas, L. J. and Odlyzko, A. M.. Periods in strings. J. Combin. Theory Ser. A 30(1) (1981), 19–42.10.1016/0097-3165(81)90038-8CrossRefGoogle Scholar
Lind, D. A.. Perturbations of shifts of finite type. SIAM J. Discrete Math. 2(3) (1989), 350–365.CrossRefGoogle Scholar
Miller, J. S.. Two notes on subshifts. Proc. Amer. Math. Soc. 140(5) (2012), 1617–1622.10.1090/S0002-9939-2011-11000-1CrossRefGoogle Scholar
Parry, W.. Intrinsic Markov chains. Trans. Amer. Math. Soc. 112 (1964), 55–66.CrossRefGoogle Scholar
Pavlov, R.. Perturbations of multidimensional shifts of finite type. Ergod. Th. & Dynam. Sys. 31(2) (2011), 483–526.10.1017/S0143385710000040CrossRefGoogle Scholar
Ramsey, N.. Perturbing subshifts of finite type: two words. Preprint, 2019, arXiv:1902.03352.Google Scholar


