Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-22T16:28:11.442Z Has data issue: false hasContentIssue false
  • English
  • Français

Ergodic properties of matrix equilibrium states

Published online by Cambridge University Press:  14 March 2017

IAN D. MORRIS
IAN D. MORRIS*
Affiliation:
Mathematics Department, University of Surrey, Guildford, GU2 7XH, UK email i.morris@surrey.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a finite irreducible set of real 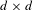$d\times d$ matrices 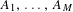$A_{1},\ldots ,A_{M}$ and a real parameter 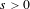$s>0$, there exists a unique shift-invariant equilibrium state on 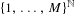$\{1,\ldots ,M\}^{\mathbb{N}}$ associated to 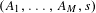$(A_{1},\ldots ,A_{M},s)$. In this paper we characterize the ergodic properties of such equilibrium states in terms of the algebraic properties of the semigroup generated by the associated matrices. We completely characterize when the equilibrium state has zero entropy, when it gives distinct Lyapunov exponents to the natural cocycle generated by 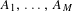$A_{1},\ldots ,A_{M}$, and when it is a Bernoulli measure. We also give a general sufficient condition for the equilibrium state to be mixing, and give an example where the equilibrium state is ergodic but not totally ergodic. Connections with a class of measures investigated by Kusuoka are explored in an appendix.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 6 , September 2018 , pp. 2295 - 2320
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bárány, B. and Rams, M.. Dimension maximizing measures for self-affine systems. Preprint, 2015, arXiv:1507.02829.Google Scholar
Bell, R., Ho, C.-W. and Strichartz, R. S.. Energy measures of harmonic functions on the Sierpiński gasket. Indiana Univ. Math. J. 63(3) (2014), 831–868.Google Scholar
Berger, M. A. and Wang, Y.. Bounded semigroups of matrices. Linear Algebra Appl. 166 (1992), 21–27.Google Scholar
Berman, A. and Plemmons, R. J.. Nonnegative Matrices in the Mathematical Sciences (Classics in Applied Mathematics, 9) . Society for Industrial and Applied Mathematics (SIAM), Philadelphia, PA, 1994, revised reprint of the 1979 original.Google Scholar
Blondel, V. D. and Nesterov, Y.. Computationally efficient approximations of the joint spectral radius. SIAM J. Matrix Anal. Appl. 27(1) (2005), 256–272 (electronic).Google Scholar
Bochi, J.. Inequalities for numerical invariants of sets of matrices. Linear Algebra Appl. 368 (2003), 71–81.Google Scholar
Bowen, R.. Bernoulli equilibrium states for Axiom A diffeomorphisms. Math. Syst. Theory 8(4) (1974/75), 289–294.Google Scholar
Cao, Y.-L., Feng, D.-J. and Huang, W.. The thermodynamic formalism for sub-additive potentials. Discrete Contin. Dyn. Syst. 20(3) (2008), 639–657.Google Scholar
Coelho, Z. and Quas, A. N.. Criteria for d -continuity. Trans. Amer. Math. Soc. 350(8) (1998), 3257–3268.Google Scholar
Elsner, L.. The generalized spectral-radius theorem: an analytic-geometric proof. Proceedings of the Workshop ‘Nonnegative Matrices, Applications and Generalizations’ and the Eighth Haifa Matrix Theory Conference (Linear Algebra and Its Applications, 220) . Elsevier, New York, 1995, pp. 151–159.Google Scholar
Falconer, K. and Kempton, T.. Planar self-affine sets with equal Hausdorff, box and affinity dimensions. Preprint, 2015, arXiv:1503.01270 Ergod. Th. & Dynam. Sys. accepted.Google Scholar
Feng, D.-J.. Lyapunov exponents for products of matrices and multifractal analysis. I. Positive matrices. Israel J. Math. 138 (2003), 353–376.Google Scholar
Feng, D.-J.. Lyapunov exponents for products of matrices and multifractal analysis. II. General matrices. Israel J. Math. 170 (2009), 355–394.Google Scholar
Feng, D.-J. and Käenmäki, A.. Equilibrium states of the pressure function for products of matrices. Discrete Contin. Dyn. Syst. 30(3) (2011), 699–708.Google Scholar
Feng, D.-J. and Lau, K.-S.. The pressure function for products of non-negative matrices. Math. Res. Lett. 9(2–3) (2002), 363–378.Google Scholar
Feng, D.-J. and Shmerkin, P.. Non-conformal repellers and the continuity of pressure for matrix cocycles. Geom. Funct. Anal. 24(4) (2014), 1101–1128.Google Scholar
Glasner, E.. Ergodic Theory via Joinings (Mathematical Surveys and Monographs, 101) . American Mathematical Society, Providence, RI, 2003.Google Scholar
Gurvits, L.. Stability of linear inclusions—part 2. NECI Technical Report TR, 1996, pp. 96–173.Google Scholar
Horn, R. A. and Johnson, C. R.. Topics in Matrix Analysis. Cambridge University Press, Cambridge, 1994, corrected reprint of the 1991 original.Google Scholar
Johansson, A., Öberg, A. and Pollicott, M.. Ergodic theory of Kusuoka measures. J. Fractal Geom. to appear.Google Scholar
Jungers, R.. The Joint Spectral Radius (Lecture Notes in Control and Information Sciences, 385) . Springer, Berlin, 2009.Google Scholar
Käenmäki, A.. On natural invariant measures on generalised iterated function systems. Ann. Acad. Sci. Fenn. Math. 29(2) (2004), 419–458.Google Scholar
Käenmäki, A. and Reeve, H. W. J.. Multifractal analysis of Birkhoff averages for typical infinitely generated self-affine sets. J. Fractal Geom. 1(1) (2014), 83–152.Google Scholar
Kusuoka, S.. Dirichlet forms on fractals and products of random matrices. Publ. Res. Inst. Math. Sci. 25(4) (1989), 659–680.Google Scholar
Lagarias, J. C. and Wang, Y.. The finiteness conjecture for the generalized spectral radius of a set of matrices. Linear Algebra Appl. 214 (1995), 17–42.Google Scholar
Lau, K.-S. and Wang, J.. Characterization of L p -solutions for the two-scale dilation equations. SIAM J. Math. Anal. 26(4) (1995), 1018–1046.Google Scholar
Morris, I. D.. Criteria for the stability of the finiteness property and for the uniqueness of Barabanov norms. Linear Algebra Appl. 433(7) (2010), 1301–1311.Google Scholar
Morris, I. D.. The generalised Berger–Wang formula and the spectral radius of linear cocycles. J. Funct. Anal. 262(3) (2012), 811–824.Google Scholar
Morris, I. D.. Mather sets for sequences of matrices and applications to the study of joint spectral radii. Proc. Lond. Math. Soc. (3) 107(1) (2013), 121–150.Google Scholar
Morris, I. D.. An inequality for the matrix pressure function and applications. Adv. Math. 302 (2016), 280–308.Google Scholar
Morris, I. D. and Shmerkin, P.. On equality of Hausdorff and affinity dimensions, via self-affine measures on positive subsystems. Preprint, 2016, arXiv:1602.08789.Google Scholar
Omladič, M. and Radjavi, H.. Irreducible semigroups with multiplicative spectral radius. Linear Algebra Appl. 251 (1997), 59–72.Google Scholar
Ornstein, D. S.. On the root problem in ergodic theory. Proceedings of the Sixth Berkeley Symposium on Mathematical Statistics and Probability, Vol. II: Probability Theory. Eds. LeCam, L., Neyman, J. and Scott, E. L.. University of California Press, Berkeley, CA, 1972, pp. 347–356.Google Scholar
Parry, W. and Pollicott, M.. Zeta functions and the periodic orbit structure of hyperbolic dynamics. Astérisque 187–188 (1990), 268.Google Scholar
Protasov, V. Y.. The generalized joint spectral radius: a geometric approach. Izv. Ross. Akad. Nauk Ser. Mat. 61(5) (1997), 99–136.Google Scholar
Protasov, V. Y.. When do several linear operators share an invariant cone? Linear Algebra Appl. 433(4) (2010), 781–789.Google Scholar
Protasov, V. Y. and Voynov, A. S.. Matrix semigroups with constant spectral radius. Preprint, 2014, arXiv:1407.6568.Google Scholar
Rota, G.-C.. Gian-Carlo Rota on Analysis and Probability: Selected Papers and Commentaries (Contemporary Mathematicians) . Eds. Dhombres, J., Kung, J. P. S. and Starr, N.. Birkhäuser, Boston, 2003.Google Scholar
Rota, G.-C. and Strang, G.. A note on the joint spectral radius. Indag. Math. 22 (1960), 379–381.Google Scholar
Shields, P. C.. The Ergodic Theory of Discrete Sample Paths (Graduate Studies in Mathematics, 13) . American Mathematical Society, Providence, RI, 1996.Google Scholar
Strichartz, R. S. and Tse, S. T.. Local behavior of smooth functions for the energy Laplacian on the Sierpinski gasket. Analysis (Munich) 30(3) (2010), 285–299.Google Scholar
Wirth, F.. The generalized spectral radius and extremal norms. Linear Algebra Appl. 342 (2002), 17–40.Google Scholar