Article contents
Flows, growth rates, and the veering polynomial
Published online by Cambridge University Press: 04 October 2022
Abstract
For a pseudo-Anosov flow 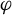 $\varphi $ without perfect fits on a closed
$\varphi $ without perfect fits on a closed 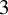 $3$-manifold, Agol–Guéritaud produce a veering triangulation
$3$-manifold, Agol–Guéritaud produce a veering triangulation 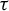 $\tau $ on the manifold M obtained by deleting the singular orbits of
$\tau $ on the manifold M obtained by deleting the singular orbits of 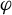 $\varphi $. We show that
$\varphi $. We show that 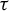 $\tau $ can be realized in M so that its 2-skeleton is positively transverse to
$\tau $ can be realized in M so that its 2-skeleton is positively transverse to 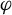 $\varphi $, and that the combinatorially defined flow graph
$\varphi $, and that the combinatorially defined flow graph 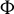 $\Phi $ embedded in M uniformly codes the orbits of
$\Phi $ embedded in M uniformly codes the orbits of 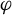 $\varphi $ in a precise sense. Together with these facts, we use a modified version of the veering polynomial, previously introduced by the authors, to compute the growth rates of the closed orbits of
$\varphi $ in a precise sense. Together with these facts, we use a modified version of the veering polynomial, previously introduced by the authors, to compute the growth rates of the closed orbits of 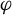 $\varphi $ after cutting M along certain transverse surfaces, thereby generalizing the work of McMullen in the fibered setting. These results are new even in the case where the transverse surface represents a class in the boundary of a fibered cone of M. Our work can be used to study the flow
$\varphi $ after cutting M along certain transverse surfaces, thereby generalizing the work of McMullen in the fibered setting. These results are new even in the case where the transverse surface represents a class in the boundary of a fibered cone of M. Our work can be used to study the flow 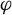 $\varphi $ on the original closed manifold. Applications include counting growth rates of closed orbits after cutting along closed transverse surfaces, defining a continuous, convex entropy function on the ‘positive’ cone in
$\varphi $ on the original closed manifold. Applications include counting growth rates of closed orbits after cutting along closed transverse surfaces, defining a continuous, convex entropy function on the ‘positive’ cone in 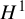 $H^1$ of the cut-open manifold, and answering a question of Leininger about the closure of the set of all stretch factors arising as monodromies within a single fibered cone of a
$H^1$ of the cut-open manifold, and answering a question of Leininger about the closure of the set of all stretch factors arising as monodromies within a single fibered cone of a 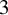 $3$-manifold. This last application connects to the study of endperiodic automorphisms of infinite-type surfaces and the growth rates of their periodic points.
$3$-manifold. This last application connects to the study of endperiodic automorphisms of infinite-type surfaces and the growth rates of their periodic points.
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
References
- 7
- Cited by


