Article contents
Generic behavior of a measure-preserving transformation
Published online by Cambridge University Press: 25 September 2018
Abstract
Del Junco–Lemańczyk [Generic spectral properties of measure-preserving maps and applications. Proc. Amer. Math. Soc., 115 (3) (1992)] showed that a generic measure-preserving transformation satisfies certain orthogonality conditions. More precisely, there is a dense 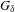 $G_{\unicode[STIX]{x1D6FF}}$ subset of measure preserving transformations such that, for every
$G_{\unicode[STIX]{x1D6FF}}$ subset of measure preserving transformations such that, for every 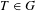 $T\in G$ and
$T\in G$ and  $k(1),k(2),\ldots ,k(l)\in \mathbb{Z}^{+}$,
$k(1),k(2),\ldots ,k(l)\in \mathbb{Z}^{+}$,  $k^{\prime }(1),k^{\prime }(2),\ldots ,k^{\prime }(l^{\prime })\in \mathbb{Z}^{+}$, the convolutions
$k^{\prime }(1),k^{\prime }(2),\ldots ,k^{\prime }(l^{\prime })\in \mathbb{Z}^{+}$, the convolutions 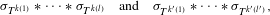 $$\begin{eqnarray}\unicode[STIX]{x1D70E}_{T^{k(1)}}\ast \cdots \ast \unicode[STIX]{x1D70E}_{T^{k(l)}}\quad \text{and}\quad \unicode[STIX]{x1D70E}_{T^{k^{\prime }(1)}}\ast \cdots \ast \unicode[STIX]{x1D70E}_{T^{k^{\prime }(l^{\prime })}},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70E}_{T^{k(1)}}\ast \cdots \ast \unicode[STIX]{x1D70E}_{T^{k(l)}}\quad \text{and}\quad \unicode[STIX]{x1D70E}_{T^{k^{\prime }(1)}}\ast \cdots \ast \unicode[STIX]{x1D70E}_{T^{k^{\prime }(l^{\prime })}},\end{eqnarray}$$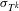 $\unicode[STIX]{x1D70E}_{T^{k}}$ is the maximal spectral type of
$\unicode[STIX]{x1D70E}_{T^{k}}$ is the maximal spectral type of 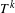 $T^{k}$, are mutually singular, provided that
$T^{k}$, are mutually singular, provided that 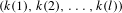 $(k(1),k(2),\ldots ,k(l))$ is not a rearrangement of
$(k(1),k(2),\ldots ,k(l))$ is not a rearrangement of 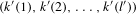 $(k^{\prime }(1),k^{\prime }(2),\ldots ,k^{\prime }(l^{\prime }))$. We will introduce analogous orthogonality conditions for continuous unitary representations of the group of all measurable functions with values in the circle,
$(k^{\prime }(1),k^{\prime }(2),\ldots ,k^{\prime }(l^{\prime }))$. We will introduce analogous orthogonality conditions for continuous unitary representations of the group of all measurable functions with values in the circle, 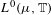 $L^{0}(\unicode[STIX]{x1D707},\mathbb{T})$, which we denote by the DL-condition. We connect the DL-condition with a result of Solecki [Unitary representations of the groups of measurable and continuous functions with values in the circle. J. Funct. Anal., 267 (2014), pp. 3105–3124] which identifies continuous unitary representations of
$L^{0}(\unicode[STIX]{x1D707},\mathbb{T})$, which we denote by the DL-condition. We connect the DL-condition with a result of Solecki [Unitary representations of the groups of measurable and continuous functions with values in the circle. J. Funct. Anal., 267 (2014), pp. 3105–3124] which identifies continuous unitary representations of 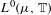 $L^{0}(\unicode[STIX]{x1D707},\mathbb{T})$ with a collection of measures
$L^{0}(\unicode[STIX]{x1D707},\mathbb{T})$ with a collection of measures 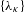 $\{\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D705}}\}$, where
$\{\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D705}}\}$, where  $\unicode[STIX]{x1D705}$ runs over all increasing finite sequence of non-zero integers. In particular, we show that the ‘probabilistic’ DL-condition translates to ‘deterministic’ orthogonality conditions on the measures
$\unicode[STIX]{x1D705}$ runs over all increasing finite sequence of non-zero integers. In particular, we show that the ‘probabilistic’ DL-condition translates to ‘deterministic’ orthogonality conditions on the measures 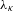 $\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D705}}$. As a corollary, we show that the same orthogonality conditions as in the result by Del Junco–Lemańczyk hold for a generic unitary operator on a separable infinite-dimensional Hilbert space.
$\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D705}}$. As a corollary, we show that the same orthogonality conditions as in the result by Del Junco–Lemańczyk hold for a generic unitary operator on a separable infinite-dimensional Hilbert space.
- Type
- Original Article
- Information
- Copyright
- © Cambridge University Press, 2018
References
- 1
- Cited by


