No CrossRef data available.
Article contents
Indistinguishable asymptotic pairs and multidimensional Sturmian configurations
Published online by Cambridge University Press: 31 May 2024
Abstract
Two asymptotic configurations on a full 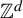 $\mathbb {Z}^d$-shift are indistinguishable if, for every finite pattern, the associated sets of occurrences in each configuration coincide up to a finitely supported permutation of
$\mathbb {Z}^d$-shift are indistinguishable if, for every finite pattern, the associated sets of occurrences in each configuration coincide up to a finitely supported permutation of 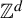 $\mathbb {Z}^d$. We prove that indistinguishable asymptotic pairs satisfying a ‘flip condition’ are characterized by their pattern complexity on finite connected supports. Furthermore, we prove that uniformly recurrent indistinguishable asymptotic pairs satisfying the flip condition are described by codimension-one (dimension of the internal space) cut and project schemes, which symbolically correspond to multidimensional Sturmian configurations. Together, the two results provide a generalization to
$\mathbb {Z}^d$. We prove that indistinguishable asymptotic pairs satisfying a ‘flip condition’ are characterized by their pattern complexity on finite connected supports. Furthermore, we prove that uniformly recurrent indistinguishable asymptotic pairs satisfying the flip condition are described by codimension-one (dimension of the internal space) cut and project schemes, which symbolically correspond to multidimensional Sturmian configurations. Together, the two results provide a generalization to 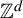 $\mathbb {Z}^d$ of the characterization of Sturmian sequences by their factor complexity
$\mathbb {Z}^d$ of the characterization of Sturmian sequences by their factor complexity 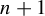 $n+1$. Many open questions are raised by the current work and are listed in the introduction.
$n+1$. Many open questions are raised by the current work and are listed in the introduction.
Keywords
MSC classification
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press


