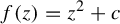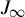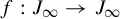1. Introduction
We consider the dynamics
![]() $f: \mathbb {C}\to \mathbb {C}$
of a quadratic polynomial. Up to a linear change of coordinates, f has the form
$f: \mathbb {C}\to \mathbb {C}$
of a quadratic polynomial. Up to a linear change of coordinates, f has the form
![]() $f_c(z)=z^2+c$
for some
$f_c(z)=z^2+c$
for some
![]() $c\in \mathbb {C}$
. In this paper, which is the sequel to [Reference Levin and Przytycki12], we assume that f is infinitely renormalizable. Moreover, in the main results we assume that f has infinitely many ‘satellite renormalizations’; see, for example, [Reference McMullen16] or below for definitions. The dynamics, geometry and topology of such a system can be very non-trivial, in particular, due to the fact that different renormalization levels are largely independent.
$c\in \mathbb {C}$
. In this paper, which is the sequel to [Reference Levin and Przytycki12], we assume that f is infinitely renormalizable. Moreover, in the main results we assume that f has infinitely many ‘satellite renormalizations’; see, for example, [Reference McMullen16] or below for definitions. The dynamics, geometry and topology of such a system can be very non-trivial, in particular, due to the fact that different renormalization levels are largely independent.
Historically, the first example of an infinitely renormalizable one-dimensional map was probably the Feigenbaum period-doubling quadratic polynomial
![]() $f_{c_F}$
, where
$f_{c_F}$
, where
![]() $c_F=-1.4\ldots $
[Reference Feigenbaum6]. The Julia set of
$c_F=-1.4\ldots $
[Reference Feigenbaum6]. The Julia set of
![]() $f_{c_F}$
is locally connected [Reference Hu and Jiang7], which follows from so-called ‘complex bounds’, a compactness property of renormalizations. This is a key tool since [Reference Sullivan28], in particular, in proving the Feigenbaum–Coullet–Tresser universality conjecture [Reference Lyubich15, Reference McMullen17, Reference Sullivan28]. Perhaps more striking for us are Douady and Hubbard’s examples of infinitely renormalizable quadratic polynomials with non-locally connected Julia sets [Reference Cheraghi and Pedramfar3, Reference Cheraghi and Shishikura4, Reference Levin9–Reference Levin11, Reference Milnor18, Reference Sorensen27]. As for the Feigenbaum polynomial
$f_{c_F}$
is locally connected [Reference Hu and Jiang7], which follows from so-called ‘complex bounds’, a compactness property of renormalizations. This is a key tool since [Reference Sullivan28], in particular, in proving the Feigenbaum–Coullet–Tresser universality conjecture [Reference Lyubich15, Reference McMullen17, Reference Sullivan28]. Perhaps more striking for us are Douady and Hubbard’s examples of infinitely renormalizable quadratic polynomials with non-locally connected Julia sets [Reference Cheraghi and Pedramfar3, Reference Cheraghi and Shishikura4, Reference Levin9–Reference Levin11, Reference Milnor18, Reference Sorensen27]. As for the Feigenbaum polynomial
![]() $f_{c_F}$
, all the renormalizations of such maps are satellite, although, contrary to
$f_{c_F}$
, all the renormalizations of such maps are satellite, although, contrary to
![]() $f_{c_F}$
, the combinatorics is unbounded (which, in turn, implies that those maps cannot have complex bounds [Reference Blokh, Levin, Oversteegen and Timorin1]).
$f_{c_F}$
, the combinatorics is unbounded (which, in turn, implies that those maps cannot have complex bounds [Reference Blokh, Levin, Oversteegen and Timorin1]).
The dynamics of every holomorphic endomorphism of the Riemann sphere
![]() $g:\hat {\mathbb {C}}\to \hat {\mathbb {C}}$
classically splits
$g:\hat {\mathbb {C}}\to \hat {\mathbb {C}}$
classically splits
![]() $\hat {\mathbb {C}}$
into two subsets: the Fatou set
$\hat {\mathbb {C}}$
into two subsets: the Fatou set
![]() $F(g)$
and its complement, the Julia set
$F(g)$
and its complement, the Julia set
![]() $J(g)$
, where
$J(g)$
, where
![]() $F(g)$
is the maximal (possibly empty) open set where the sequence of iterates
$F(g)$
is the maximal (possibly empty) open set where the sequence of iterates
![]() $g^n$
,
$g^n$
,
![]() $n=0,1,\ldots $
forms a normal (that is, a precompact) family. See, for example, [Reference Carleson and Gamelin2, Reference Milnor20] for the Fatou–Julia theory and [Reference Rees26] for a recent survey.
$n=0,1,\ldots $
forms a normal (that is, a precompact) family. See, for example, [Reference Carleson and Gamelin2, Reference Milnor20] for the Fatou–Julia theory and [Reference Rees26] for a recent survey.
If g is a polynomial, then the Julia set
![]() $J(g)$
coincides with the boundary of the basin of infinity
$J(g)$
coincides with the boundary of the basin of infinity
![]() $A(\infty )=\{z\in \mathbb {C}| \lim _{n\to \infty }g^n(z)=\infty \}$
of g. The complement
$A(\infty )=\{z\in \mathbb {C}| \lim _{n\to \infty }g^n(z)=\infty \}$
of g. The complement
![]() $\mathbb {C}\setminus A(g)$
is called the filled Julia set
$\mathbb {C}\setminus A(g)$
is called the filled Julia set
![]() $K(g)$
of the polynomial g. The compact
$K(g)$
of the polynomial g. The compact
![]() $K(g)\subset \mathbb {C}$
is connected if and only if it contains all critical points of g in the complex plane.
$K(g)\subset \mathbb {C}$
is connected if and only if it contains all critical points of g in the complex plane.
A quadratic polynomial
![]() $f_c$
with connected filled Julia set
$f_c$
with connected filled Julia set
![]() $K(f)$
is renormalizable if, for some topological disks
$K(f)$
is renormalizable if, for some topological disks
![]() $U\Subset V$
around the critical point
$U\Subset V$
around the critical point
![]() $0$
of
$0$
of
![]() $f_c$
and some
$f_c$
and some
![]() $p\ge 2$
(period of renormalization), the restriction
$p\ge 2$
(period of renormalization), the restriction
![]() $F:=f_c^p:U\to V$
is a proper branched covering map (called a polynomial-like map) of degree
$F:=f_c^p:U\to V$
is a proper branched covering map (called a polynomial-like map) of degree
![]() $2$
and the non-escaping set
$2$
and the non-escaping set
![]() $K(F){\kern-1pt}={\kern-1pt}\{z\in U: F^{n}(z){\kern-1pt}\in{\kern-1pt} U \text { for all } n{\kern-1pt}\ge{\kern-1pt} 1\}$
(called the filled Julia set of the polynomial-like map F) is connected. The map
$K(F){\kern-1pt}={\kern-1pt}\{z\in U: F^{n}(z){\kern-1pt}\in{\kern-1pt} U \text { for all } n{\kern-1pt}\ge{\kern-1pt} 1\}$
(called the filled Julia set of the polynomial-like map F) is connected. The map
![]() $F:U\to V$
is then a renormalization of
$F:U\to V$
is then a renormalization of
![]() $f_c$
and the set
$f_c$
and the set
![]() $K(F)$
is a ‘small’ (filled) Julia set of
$K(F)$
is a ‘small’ (filled) Julia set of
![]() $f_c$
. By the theory of polynomial-like mappings [Reference Douady and Hubbard5], there is a quasiconformal homeomorphism of
$f_c$
. By the theory of polynomial-like mappings [Reference Douady and Hubbard5], there is a quasiconformal homeomorphism of
![]() $\mathbb {C}$
, which is conformal on
$\mathbb {C}$
, which is conformal on
![]() $K(F)$
, that conjugates F on a neighborhood of
$K(F)$
, that conjugates F on a neighborhood of
![]() $K(F)$
to another uniquely defined quadratic polynomial
$K(F)$
to another uniquely defined quadratic polynomial
![]() $f_{c'}$
with connected filled Julia set. If
$f_{c'}$
with connected filled Julia set. If
![]() $f_{c'}$
is renormalizable by itself, then
$f_{c'}$
is renormalizable by itself, then
![]() $f_c$
is called twice renormalizable, etc. If
$f_c$
is called twice renormalizable, etc. If
![]() $f_c$
admits infinitely many renormalizations, it is called infinitely renormalizable. The renormalization
$f_c$
admits infinitely many renormalizations, it is called infinitely renormalizable. The renormalization
![]() $F=f^p_c$
is simple if any two sets
$F=f^p_c$
is simple if any two sets
![]() $f^i(K(f))$
,
$f^i(K(f))$
,
![]() $f^j(K(F))$
,
$f^j(K(F))$
,
![]() $0\le i<j\le p-1$
, are either disjoint or intersect each other at a unique point which does not separate either of them. A simple renormalization
$0\le i<j\le p-1$
, are either disjoint or intersect each other at a unique point which does not separate either of them. A simple renormalization
![]() $f^{p_n}$
is called primitive if all sets
$f^{p_n}$
is called primitive if all sets
![]() $f^i(K_n)$
,
$f^i(K_n)$
,
![]() $i=0,\ldots , p_n-1$
, are disjoints and satellite otherwise.
$i=0,\ldots , p_n-1$
, are disjoints and satellite otherwise.
To state our main result, Theorem 1.1, let
![]() $f(z)=z^2+c$
be infinitely renormalizable. Then its Julia set
$f(z)=z^2+c$
be infinitely renormalizable. Then its Julia set
![]() $J=J(f)$
coincides with the filled Julia set
$J=J(f)$
coincides with the filled Julia set
![]() $K(f)$
and is a nowhere dense compact full connected subset of
$K(f)$
and is a nowhere dense compact full connected subset of
![]() $\mathbb {C}$
. Let
$\mathbb {C}$
. Let
![]() $1=p_0<p_1<\cdots <p_n<\cdots $
be the sequence of consecutive periods of simple renormalizations of f and
$1=p_0<p_1<\cdots <p_n<\cdots $
be the sequence of consecutive periods of simple renormalizations of f and
![]() $J_n\ni 0$
denote the ‘small’ Julia set of the n-renormalization (where
$J_n\ni 0$
denote the ‘small’ Julia set of the n-renormalization (where
![]() $J_0=J$
). Then
$J_0=J$
). Then
![]() $p_{n+1}/p_n$
is an integer,
$p_{n+1}/p_n$
is an integer,
![]() $f^{p_n}(J_n)=J_n$
, for any n, and f-orbits of
$f^{p_n}(J_n)=J_n$
, for any n, and f-orbits of
![]() $J_n$
,
$J_n$
,
 $$ \begin{align*} \mathrm{orb}(J_n)=\bigcup_{j\ge 0}f^j(J_n)=\bigcup_{j=0}^{p_n-1}f^j(J_n),\end{align*} $$
$$ \begin{align*} \mathrm{orb}(J_n)=\bigcup_{j\ge 0}f^j(J_n)=\bigcup_{j=0}^{p_n-1}f^j(J_n),\end{align*} $$
![]() $n=0,1,\ldots ,$
form a strictly decreasing sequence of compact subsets of
$n=0,1,\ldots ,$
form a strictly decreasing sequence of compact subsets of
![]() $\mathbb {C}$
. Let
$\mathbb {C}$
. Let
be the intersection of the orbits of the ‘small’ Julia sets
![]() $J_n$
. For every n, repelling periodic orbits of f are dense in
$J_n$
. For every n, repelling periodic orbits of f are dense in
![]() $\mathrm {orb}(J_n)$
, while each component of
$\mathrm {orb}(J_n)$
, while each component of
![]() $J_\infty $
is wandering. In particular,
$J_\infty $
is wandering. In particular,
![]() $J_\infty $
contains no periodic points of f.
$J_\infty $
contains no periodic points of f.
Let
be the postcritical set of f. Clearly,
Moreover, the critical point
![]() $0$
is recurrent, hence,
$0$
is recurrent, hence,
where
![]() $\omega (z)$
is the omega-limit set of a point
$\omega (z)$
is the omega-limit set of a point
![]() $z\in J$
.
$z\in J$
.
We prove in [Reference Levin and Przytycki12] that
![]() $J_\infty $
cannot contain any hyperbolic set. On the other hand, a hyperbolic set of a rational map always carries an invariant measure with a positive Lyapunov exponent. So a generalization of [Reference Levin and Przytycki12] would be that
$J_\infty $
cannot contain any hyperbolic set. On the other hand, a hyperbolic set of a rational map always carries an invariant measure with a positive Lyapunov exponent. So a generalization of [Reference Levin and Przytycki12] would be that
![]() $J_\infty $
never carries such a measure. Here we prove this generalization for a class of ‘satellite’ infinitely renormalizable quadratic polynomials.
$J_\infty $
never carries such a measure. Here we prove this generalization for a class of ‘satellite’ infinitely renormalizable quadratic polynomials.
Theorem 1.1. Suppose that
![]() $f(z)=z^2+c$
admits infinitely many satellite renormalizations. Then
$f(z)=z^2+c$
admits infinitely many satellite renormalizations. Then
![]() $f: J_\infty \to J_\infty $
has no invariant probability measure with positive Lyapunov exponent.
$f: J_\infty \to J_\infty $
has no invariant probability measure with positive Lyapunov exponent.
Remark 1.1. Conjecturally, the same conclusion should hold for any infinitely renormalizable
![]() $f(z)=z^2+c$
. One can show this assuming that the Julia set of f is locally connected (for example, this is the case if f admits complex bounds). Indeed, if
$f(z)=z^2+c$
. One can show this assuming that the Julia set of f is locally connected (for example, this is the case if f admits complex bounds). Indeed, if
![]() $f:J_\infty \to J_\infty $
had an invariant probability measure with positive Lyapunov exponent, then, taking a typical point of this measure and repeating the proof of [Reference Levin, Przytycki and Shen13, Corollary 5.5], we would conclude that the Julia set of f is not locally connected (in fact,
$f:J_\infty \to J_\infty $
had an invariant probability measure with positive Lyapunov exponent, then, taking a typical point of this measure and repeating the proof of [Reference Levin, Przytycki and Shen13, Corollary 5.5], we would conclude that the Julia set of f is not locally connected (in fact,
![]() $J_\infty $
contains a non-trivial continuum). Thus the only open case remains when f has only finitely many satellite renormalizations and
$J_\infty $
contains a non-trivial continuum). Thus the only open case remains when f has only finitely many satellite renormalizations and
![]() $J_\infty $
contains a non-trivial continuum.
$J_\infty $
contains a non-trivial continuum.
Remark 1.2. For every rational map
![]() $f:\mathbb {C}\to \mathbb {C}$
(in particular, quadratic polynomial) and every invariant probability measure supported on the Julia set of f, the Lyapunov exponent is non-negative: see [Reference Przytycki22] (compare a remark preceding Corollary 1.3). On the other hand, if f is hyperbolic or non-uniformly hyperbolic (topologically Collet–Eckmann), Lyapunov exponents for all invariant probability measures supported on the Julia set are positive and bounded away from
$f:\mathbb {C}\to \mathbb {C}$
(in particular, quadratic polynomial) and every invariant probability measure supported on the Julia set of f, the Lyapunov exponent is non-negative: see [Reference Przytycki22] (compare a remark preceding Corollary 1.3). On the other hand, if f is hyperbolic or non-uniformly hyperbolic (topologically Collet–Eckmann), Lyapunov exponents for all invariant probability measures supported on the Julia set are positive and bounded away from
![]() $0$
; see [Reference Przytycki24].
$0$
; see [Reference Przytycki24].
Let us comment on the behavior of the restriction map
![]() $f: J_\infty \to J_\infty $
where f as in Theorem 1.1. First, by [Reference Levin and Przytycki12], the postcritical set P must intersect the omega-limit set
$f: J_\infty \to J_\infty $
where f as in Theorem 1.1. First, by [Reference Levin and Przytycki12], the postcritical set P must intersect the omega-limit set
![]() $\omega (x)$
of each
$\omega (x)$
of each
![]() $x\in J_\infty $
. At the same time, the dynamics and topology of the further restriction
$x\in J_\infty $
. At the same time, the dynamics and topology of the further restriction
![]() ${f: P\to P}$
can vary. Indeed, there are infinitely renormalizable quadratic polynomials f with all renormalizations being of satellite type such that at least one of the following statements holds. (A more complete description of
${f: P\to P}$
can vary. Indeed, there are infinitely renormalizable quadratic polynomials f with all renormalizations being of satellite type such that at least one of the following statements holds. (A more complete description of
![]() $f:P\to P$
should follow from the methods developed in [Reference Cheraghi and Pedramfar3].)
$f:P\to P$
should follow from the methods developed in [Reference Cheraghi and Pedramfar3].)
(1)
![]() $f:P\to P$
is not minimal. This case occurs in Douady–Hubbard type examples. Indeed, by the basic construction [Reference Milnor18],
$f:P\to P$
is not minimal. This case occurs in Douady–Hubbard type examples. Indeed, by the basic construction [Reference Milnor18],
![]() $J_\infty $
then contains a closed invariant set X (which is the limit set for the collection of
$J_\infty $
then contains a closed invariant set X (which is the limit set for the collection of
![]() $\alpha $
-fixed points of renormalizations) such that
$\alpha $
-fixed points of renormalizations) such that
![]() $0\notin X$
. By [Reference Levin and Przytycki12],
$0\notin X$
. By [Reference Levin and Przytycki12],
![]() $X\cap P$
is non-empty. Thus
$X\cap P$
is non-empty. Thus
![]() $X\cap P$
is an invariant non-empty proper compact subset of P.
$X\cap P$
is an invariant non-empty proper compact subset of P.
(2) P is a so-called ‘hairy’ Cantor set; in particular, P contains uncountably many non-trivial continua. This case occurs following [Reference Cheraghi and Pedramfar3].
(3) P is a Cantor set and
![]() $f:P\to P$
is minimal; this happens whenever f either admits complex bounds (which then imply
$f:P\to P$
is minimal; this happens whenever f either admits complex bounds (which then imply
![]() $J_\infty =P$
) or is robust [Reference McMullen16]. (The ‘robustness’ can happen without ‘complex bounds’, which follows from [Reference Cheraghi and Pedramfar3] combined with [Reference Blokh, Levin, Oversteegen and Timorin1].) Under either of the two conditions,
$J_\infty =P$
) or is robust [Reference McMullen16]. (The ‘robustness’ can happen without ‘complex bounds’, which follows from [Reference Cheraghi and Pedramfar3] combined with [Reference Blokh, Levin, Oversteegen and Timorin1].) Under either of the two conditions,
![]() $f: P\to P$
is a minimal homeomorphism, which is topologically conjugate to
$f: P\to P$
is a minimal homeomorphism, which is topologically conjugate to
![]() $x\mapsto x+1$
acting on the projective limit of the sequence of groups
$x\mapsto x+1$
acting on the projective limit of the sequence of groups
![]() $\{\mathbb {Z}/p_n\mathbb {Z}\}_{n=1}^\infty $
; in particular,
$\{\mathbb {Z}/p_n\mathbb {Z}\}_{n=1}^\infty $
; in particular,
![]() $f:P\to P$
(hence, also
$f:P\to P$
(hence, also
![]() $f:J_\infty \to J_\infty $
, which follows from Corollary 1.3) is uniquely ergodic in this case.
$f:J_\infty \to J_\infty $
, which follows from Corollary 1.3) is uniquely ergodic in this case.
Theorem 1.1 yields the following dichotomy about the measurable dynamics of
![]() $f: J \to J$
on the Julia set J of f. Recall that, by [Reference Przytycki22], any invariant probability measure on the Julia set of a rational function has non-negative exponents.
$f: J \to J$
on the Julia set J of f. Recall that, by [Reference Przytycki22], any invariant probability measure on the Julia set of a rational function has non-negative exponents.
Corollary 1.3. Let
![]() $\mu $
be an invariant probability ergodic measure of
$\mu $
be an invariant probability ergodic measure of
![]() $f: J\to J$
. Then either
$f: J\to J$
. Then either
-
(i)
 $\operatorname {\mathrm {supp}}(\mu )\cap J_\infty =\emptyset $
and its Lyapunov exponent
$\operatorname {\mathrm {supp}}(\mu )\cap J_\infty =\emptyset $
and its Lyapunov exponent
 $\chi (\mu )>0$
, or
$\chi (\mu )>0$
, or -
(ii)
 $\operatorname {\mathrm {supp}}(\mu )\subset P$
and
$\operatorname {\mathrm {supp}}(\mu )\subset P$
and
 $\chi (\mu )=0$
.
$\chi (\mu )=0$
.
In particular, the set
![]() $J_\infty \setminus P$
is ‘measure invisible’ (see also Proposition 6.1 which is a somewhat stronger version of Corollary 1.3).
$J_\infty \setminus P$
is ‘measure invisible’ (see also Proposition 6.1 which is a somewhat stronger version of Corollary 1.3).
Corollary 1.4. If f admits infinitely many satellite renormalizations, then
and
For the proof of Corollaries 1.3–1.4, see §6. The proof of Theorem 1.1 occupies §§2–5.
As in [Reference Levin and Przytycki12], we make heavy use of a general result of [Reference Przytycki23] on the accessibility, although the main idea of the proof is different. Indeed, in [Reference Levin and Przytycki12] we utilize the fact that the map cannot be one-to-one on an infinite hyperbolic set. In the present paper, to prove Theorem 1.1 we assign, loosely speaking, an external ray to a typical point of a hypothetical measure with positive exponent such that the family of such rays is invariant and has a controlled geometry. Given a satellite renormalization
![]() $f^{p_n}$
, we use the measure and the above family of rays to choose a point x and build a special domain that covers a ‘small’ Julia set
$f^{p_n}$
, we use the measure and the above family of rays to choose a point x and build a special domain that covers a ‘small’ Julia set
![]() $J_{n,x}\ni x$
such that there is a univalent pullback of the domain by
$J_{n,x}\ni x$
such that there is a univalent pullback of the domain by
![]() $f^{p_n}$
along the renormalization that enters into itself, leading to a contradiction. The choice of x is ‘probabilistic’, that is, made from sets of positive measure, and the construction of the domain differs substantially depending on whether all satellite renormalizations of f are doubling or not.
$f^{p_n}$
along the renormalization that enters into itself, leading to a contradiction. The choice of x is ‘probabilistic’, that is, made from sets of positive measure, and the construction of the domain differs substantially depending on whether all satellite renormalizations of f are doubling or not.
2. Preliminaries
Here we collect, for further reference and use throughout the paper, necessary notation and general facts. Statements (A)–(D) below are slightly adapted versions of (A)–(D) in [Reference Levin and Przytycki12] which are either well known [Reference McMullen16, Reference Milnor19] or proved here.
Let
![]() $f(z)=z^2+c$
be infinitely renormalizable. We retain the notation of the Introduction.
$f(z)=z^2+c$
be infinitely renormalizable. We retain the notation of the Introduction.
(A) Let G be the Green function of the basin of infinity
![]() $A(\infty )=\{z| f^n(z)\to \infty , {n\to \infty }\}$
of f with the standard normalization at infinity
$A(\infty )=\{z| f^n(z)\to \infty , {n\to \infty }\}$
of f with the standard normalization at infinity
![]() $G(z)=\ln |z|+O(1/|z|)$
. The external ray
$G(z)=\ln |z|+O(1/|z|)$
. The external ray
![]() $R_t$
of the argument
$R_t$
of the argument
![]() $t\in \mathbf {S}^1=\mathbb {R}/\mathbb {Z}$
is a gradient line to the level sets of G that has the (asymptotic) argument t at
$t\in \mathbf {S}^1=\mathbb {R}/\mathbb {Z}$
is a gradient line to the level sets of G that has the (asymptotic) argument t at
![]() $\infty $
.
$\infty $
.
![]() $G(z)$
is called the (Green) level of
$G(z)$
is called the (Green) level of
![]() $z\in A(\infty )$
and the unique t such that
$z\in A(\infty )$
and the unique t such that
![]() $z\in R_t$
is called the (external) argument (or angle) of z. A point
$z\in R_t$
is called the (external) argument (or angle) of z. A point
![]() $z\in J(f)$
is accessible if there is an external ray
$z\in J(f)$
is accessible if there is an external ray
![]() $R_t$
which lands at (that is, converges to) z. Then t is called an (external) argument (angle) of z.
$R_t$
which lands at (that is, converges to) z. Then t is called an (external) argument (angle) of z.
Let
![]() $\sigma : \mathbf {S}^1\to \mathbf {S}^1$
be the doubling map
$\sigma : \mathbf {S}^1\to \mathbf {S}^1$
be the doubling map
![]() $\sigma (t)=2t(\mathrm {mod}\ 1)$
. Then
$\sigma (t)=2t(\mathrm {mod}\ 1)$
. Then
![]() $f(R_t)=R_{\sigma (t)}$
.
$f(R_t)=R_{\sigma (t)}$
.
Every point a of a repelling cycle
![]() $O_a$
of period p is the landing point of an equal number
$O_a$
of period p is the landing point of an equal number
![]() $v, 1\le v<\infty $
, of external rays where v coincides with the number of connected components of
$v, 1\le v<\infty $
, of external rays where v coincides with the number of connected components of
![]() $J(f)\setminus \{a\}$
. Their arguments are permuted by
$J(f)\setminus \{a\}$
. Their arguments are permuted by
![]() $\sigma ^p$
according to a rational rotation number
$\sigma ^p$
according to a rational rotation number
![]() $r/q$
(written in lowest terms);
$r/q$
(written in lowest terms);
![]() $v/q$
is the number of cycles of rays landing at a. If
$v/q$
is the number of cycles of rays landing at a. If
![]() $v/q\ge 2$
, there is an alternative [Reference Milnor19]: if
$v/q\ge 2$
, there is an alternative [Reference Milnor19]: if
![]() $r/q=0/1$
, then
$r/q=0/1$
, then
![]() $v=2$
so that each of two external rays landing at a is fixed by
$v=2$
so that each of two external rays landing at a is fixed by
![]() $f^p$
; if
$f^p$
; if
![]() $r/q\neq 0/1$
, that is,
$r/q\neq 0/1$
, that is,
![]() $q\ge 2$
, then
$q\ge 2$
, then
![]() $v=q$
, that is, the arguments of q rays landing at a form a single cycle of
$v=q$
, that is, the arguments of q rays landing at a form a single cycle of
![]() $\sigma ^p$
.
$\sigma ^p$
.
(B) All periodic points of f are repelling. Given a small Julia set
![]() $J_n$
containing
$J_n$
containing
![]() $0$
, the sets
$0$
, the sets
![]() $f^j(J_n)$
,
$f^j(J_n)$
,
![]() $0\le j< p_n$
, are called small Julia sets of level n. Each
$0\le j< p_n$
, are called small Julia sets of level n. Each
![]() $f^j(J_n)$
contains
$f^j(J_n)$
contains
![]() $p_{n+1}/p_n\ge 2$
small Julia sets of level
$p_{n+1}/p_n\ge 2$
small Julia sets of level
![]() $n+1$
. We have
$n+1$
. We have
![]() $J_n=-J_n$
. Since all renormalizations are simple, for
$J_n=-J_n$
. Since all renormalizations are simple, for
![]() $j\neq 0$
, the symmetric companion
$j\neq 0$
, the symmetric companion
![]() $-f^j(J_n)$
of
$-f^j(J_n)$
of
![]() $f^j(J_n)$
can intersect the orbit
$f^j(J_n)$
can intersect the orbit
![]() $\mathrm {orb}(J_n)=\bigcup _{j=0}^{p_n-1}f^j(J_n)$
of
$\mathrm {orb}(J_n)=\bigcup _{j=0}^{p_n-1}f^j(J_n)$
of
![]() $J_n$
only at a single point which is periodic. On the other hand, since only finitely many external rays converge to each periodic point of f, the set
$J_n$
only at a single point which is periodic. On the other hand, since only finitely many external rays converge to each periodic point of f, the set
![]() $J_\infty $
contains no periodic points. In particular, each component K of
$J_\infty $
contains no periodic points. In particular, each component K of
![]() $J_\infty $
is wandering, that is,
$J_\infty $
is wandering, that is,
![]() $f^i(K)\cap f^j(K)=\emptyset $
for all
$f^i(K)\cap f^j(K)=\emptyset $
for all
![]() $0\le i<j<\infty $
. All this implies that
$0\le i<j<\infty $
. All this implies that
![]() $\{x,-x\}\subset J_\infty $
if and only if
$\{x,-x\}\subset J_\infty $
if and only if
![]() $x\in K_0:=\bigcap _{n=1}^\infty J_n$
.
$x\in K_0:=\bigcap _{n=1}^\infty J_n$
.
Given
![]() $x\in J_\infty $
, for every n, let
$x\in J_\infty $
, for every n, let
![]() $j_n(x)$
be the unique
$j_n(x)$
be the unique
![]() $j\in \{0,1,\ldots , p_n-1\}$
such that
$j\in \{0,1,\ldots , p_n-1\}$
such that
![]() $x\in f^{j_n(x)}(J_n)$
. Let
$x\in f^{j_n(x)}(J_n)$
. Let
![]() $J_{n,x}=f^{j_n(x)}(J_n)$
be a small Julia set of level n containing x and
$J_{n,x}=f^{j_n(x)}(J_n)$
be a small Julia set of level n containing x and
![]() $K_x=\bigcap _{n\ge 0}J_{n,x}$
, a component of
$K_x=\bigcap _{n\ge 0}J_{n,x}$
, a component of
![]() $J_\infty $
containing x.
$J_\infty $
containing x.
In particular,
![]() $K_0=\bigcap _{n\ge 0}J_n$
is the component of
$K_0=\bigcap _{n\ge 0}J_n$
is the component of
![]() $J_\infty $
containing
$J_\infty $
containing
![]() $0$
and
$0$
and
![]() $K_c=\bigcap _{n=1}^\infty f(J_n)$
, the component containing c.
$K_c=\bigcap _{n=1}^\infty f(J_n)$
, the component containing c.
Note that either
![]() $p_n-j_n(x)\to \infty $
as
$p_n-j_n(x)\to \infty $
as
![]() $n\to \infty $
or
$n\to \infty $
or
![]() $p_n-j_n(x)=N$
for some
$p_n-j_n(x)=N$
for some
![]() $N\ge 0$
and all n, that is,
$N\ge 0$
and all n, that is,
![]() $f^N(x)\in K_0$
. This is so since the sequence of the sets
$f^N(x)\in K_0$
. This is so since the sequence of the sets
![]() $J_n$
is non-increasing, hence
$J_n$
is non-increasing, hence
![]() $J_{n,x}$
is non-increasing, hence
$J_{n,x}$
is non-increasing, hence
![]() $p_n-j_n(x)$
(the time to reach
$p_n-j_n(x)$
(the time to reach
![]() $J_n$
) is non-decreasing.
$J_n$
) is non-decreasing.
The map
![]() $f:K_x\to K_{f(x)}$
is two-to-one if
$f:K_x\to K_{f(x)}$
is two-to-one if
![]() $x=0$
and one-to-one otherwise. Moreover, for every
$x=0$
and one-to-one otherwise. Moreover, for every
![]() $y\in J_\infty $
,
$y\in J_\infty $
,
![]() $f^{-1}(y)\cap J_\infty $
consists of two points if
$f^{-1}(y)\cap J_\infty $
consists of two points if
![]() $y\in K_c$
and consists of a single point otherwise. Denote
$y\in K_c$
and consists of a single point otherwise. Denote
 $$ \begin{align*}J_\infty'=J_\infty\setminus\bigcup_{j=-\infty}^\infty f^j(K_0). \end{align*} $$
$$ \begin{align*}J_\infty'=J_\infty\setminus\bigcup_{j=-\infty}^\infty f^j(K_0). \end{align*} $$
We conclude that
![]() $f: J_\infty '\to J_\infty '$
is a homeomorphism. Given
$f: J_\infty '\to J_\infty '$
is a homeomorphism. Given
![]() $x\in J_\infty '$
and
$x\in J_\infty '$
and
![]() $m>0$
, denote
$m>0$
, denote
![]() $x_m=f^m(x)$
and
$x_m=f^m(x)$
and
that is, the only point
![]() $f^{-m}(x)\cap J_\infty $
.
$f^{-m}(x)\cap J_\infty $
.
(C) Given
![]() $n\ge 0$
, the map
$n\ge 0$
, the map
![]() $f^{p_n}:f(J_n)\to f(J_n)$
has two fixed points: the separating fixed point
$f^{p_n}:f(J_n)\to f(J_n)$
has two fixed points: the separating fixed point
![]() $\alpha _n$
(that is,
$\alpha _n$
(that is,
![]() $f(J_n)\setminus \{\alpha _n\}$
has at least two components) and the non-separating
$f(J_n)\setminus \{\alpha _n\}$
has at least two components) and the non-separating
![]() $\beta _n$
(so that
$\beta _n$
(so that
![]() $f(J_n)\setminus \beta _n$
has a single component).
$f(J_n)\setminus \beta _n$
has a single component).
For every
![]() $n>0$
, there are
$n>0$
, there are
![]() $0<t_n<\tilde t_n<1$
such that two rays
$0<t_n<\tilde t_n<1$
such that two rays
![]() $R_{t_n}$
and
$R_{t_n}$
and
![]() $R_{\tilde t_n}$
land at the non-separating fixed point
$R_{\tilde t_n}$
land at the non-separating fixed point
![]() $\beta _n\in f(J_n)$
of
$\beta _n\in f(J_n)$
of
![]() $f^{p_n}$
and the component
$f^{p_n}$
and the component
![]() $\Omega _n$
of
$\Omega _n$
of
![]() $\mathbb {C}\setminus {(R_{t_n}\cup R_{\tilde t_n}\cup \beta _n)}$
which does not contain
$\mathbb {C}\setminus {(R_{t_n}\cup R_{\tilde t_n}\cup \beta _n)}$
which does not contain
![]() $0$
has two characteristic properties [Reference Milnor19]:
$0$
has two characteristic properties [Reference Milnor19]:
(i)
![]() $\Omega _n$
contains c and is disjoint with the forward orbit of
$\Omega _n$
contains c and is disjoint with the forward orbit of
![]() $\beta _n$
.
$\beta _n$
.
(ii) For every
![]() $1\le j<p_n$
, consider arguments (angles) of external rays which land at
$1\le j<p_n$
, consider arguments (angles) of external rays which land at
![]() $f^{j-1}(\beta _n)$
. The angles split
$f^{j-1}(\beta _n)$
. The angles split
![]() $\mathbf {S}^1$
into finitely many arcs. Then the length of any such arc is bigger than the length of the arc
$\mathbf {S}^1$
into finitely many arcs. Then the length of any such arc is bigger than the length of the arc
Denote
The rays
![]() $R_{t_n'}$
,
$R_{t_n'}$
,
![]() $R_{\tilde t_n'}$
land at a common point
$R_{\tilde t_n'}$
land at a common point
![]() $\beta _n'\in f^{-p_n}(\beta _n)\cap \Omega _n$
. Introduce an (unbounded) domain
$\beta _n'\in f^{-p_n}(\beta _n)\cap \Omega _n$
. Introduce an (unbounded) domain
![]() $U_n$
with boundary consisting of two curves
$U_n$
with boundary consisting of two curves
![]() $R_{t_n}\cup R_{\tilde t_n}\cup \beta _n$
and
$R_{t_n}\cup R_{\tilde t_n}\cup \beta _n$
and
![]() $R_{t_n'}\cup R_{\tilde t_n'}\cup \beta _n'$
. Then
$R_{t_n'}\cup R_{\tilde t_n'}\cup \beta _n'$
. Then
![]() $c\in U_n$
and
$c\in U_n$
and
![]() $f^{p_n}: U_n\to \Omega _n$
is a two-to-one branched covering. Also,
$f^{p_n}: U_n\to \Omega _n$
is a two-to-one branched covering. Also,
Let
so that
![]() $s_{n,1}\subset S_{n,1}$
and the argument of any ray to
$s_{n,1}\subset S_{n,1}$
and the argument of any ray to
![]() $f(J_n)$
lies in
$f(J_n)$
lies in
![]() $s_{n,1}$
.
$s_{n,1}$
.
Let us iterate this construction. Given
![]() $1\le j\le p_n$
, let
$1\le j\le p_n$
, let
![]() $S_{n,j}$
be one of the two arcs of
$S_{n,j}$
be one of the two arcs of
![]() $\mathbf {S}^1$
with end points
$\mathbf {S}^1$
with end points
such that arguments of any ray to
![]() $f^{j}(J_n)$
lies in
$f^{j}(J_n)$
lies in
![]() $S_{n,j}$
. Let
$S_{n,j}$
. Let
where
![]() $t_{n,j}'=\sigma ^{j-1}(t_n'), \tilde t_{n,j}'=\sigma ^{j-1}(\tilde t_n')$
. Then
$t_{n,j}'=\sigma ^{j-1}(t_n'), \tilde t_{n,j}'=\sigma ^{j-1}(\tilde t_n')$
. Then
and the argument of any ray to
![]() $f^j(J_n)$
lies in fact in
$f^j(J_n)$
lies in fact in
![]() $s_{n,j}$
. Note that
$s_{n,j}$
. Note that
So
![]() $\sigma ^{j-1}: s_{n,1}\to s_{n,j}$
is a homeomorphism and
$\sigma ^{j-1}: s_{n,1}\to s_{n,j}$
is a homeomorphism and
![]() $s_{n,j}$
has two components (‘windows’)
$s_{n,j}$
has two components (‘windows’)
![]() $[t_{n,j}, t_{n,j}']$
and
$[t_{n,j}, t_{n,j}']$
and
![]() $[\tilde t_{n,j}', \tilde t_{n,j}]$
of equal length.
$[\tilde t_{n,j}', \tilde t_{n,j}]$
of equal length.
Let
![]() $U_{n,j}=f^{j-1}(U_n)$
and
$U_{n,j}=f^{j-1}(U_n)$
and
![]() $\beta _{n,j}=f^{j-1}(\beta _n)$
. The domain
$\beta _{n,j}=f^{j-1}(\beta _n)$
. The domain
![]() $U_{n,j}$
is bounded by two rays
$U_{n,j}$
is bounded by two rays
![]() $R_{t_{n,j}}\cup R_{\tilde t_{n,j}}$
converging to
$R_{t_{n,j}}\cup R_{\tilde t_{n,j}}$
converging to
![]() $\beta _{n,j}$
and completed by
$\beta _{n,j}$
and completed by
![]() $\beta _{n,j}$
along with two rays
$\beta _{n,j}$
along with two rays
![]() $R_{t_{n,j}'}\cup R_{\tilde t_{n,j}'}$
completed by their common limit point
$R_{t_{n,j}'}\cup R_{\tilde t_{n,j}'}$
completed by their common limit point
![]() $f^{j-1}(\beta _n')$
where
$f^{j-1}(\beta _n')$
where
![]() $t_{n,j}'=\sigma ^{j-1}(t_n'), \tilde t_{n,j}'=\sigma ^{j-1}(\tilde t_n')$
.
$t_{n,j}'=\sigma ^{j-1}(t_n'), \tilde t_{n,j}'=\sigma ^{j-1}(\tilde t_n')$
.
By (i) and (ii), for a fixed n, the domains
![]() $U_{n,j}$
,
$U_{n,j}$
,
![]() $1\le j\le p_n$
, are pairwise disjoint.
$1\le j\le p_n$
, are pairwise disjoint.
Let
![]() $U_{n,j-p_n}$
be a component of
$U_{n,j-p_n}$
be a component of
![]() $f^{-(p_n-j)}(U_n)$
which is contained in
$f^{-(p_n-j)}(U_n)$
which is contained in
![]() $U_{n,j}$
. Then
$U_{n,j}$
. Then
is a two-to-one branched covering and
Let
![]() $s^1_{n,j}$
be the set of arguments of rays entering
$s^1_{n,j}$
be the set of arguments of rays entering
![]() $U_{n,j-p_n}$
. Then
$U_{n,j-p_n}$
. Then
![]() $s^1_{n,j}$
consists of four components so that the
$s^1_{n,j}$
consists of four components so that the
![]() $\sigma ^{p_n}$
map each of these components homeomorphically onto one of the ‘windows’ of
$\sigma ^{p_n}$
map each of these components homeomorphically onto one of the ‘windows’ of
![]() $s_{n,j}$
.
$s_{n,j}$
.
Furthermore, let
Unlike the map (2.2), the map
is a two-to-one branched covering only assuming
![]() $f^{j-1}: \Omega _{n}\to \Omega _{n,j}$
is a homeomorphism, which holds if and only if
$f^{j-1}: \Omega _{n}\to \Omega _{n,j}$
is a homeomorphism, which holds if and only if
![]() $\sigma ^{j-1}: S_{n,1}\to \sigma ^{j-1}(S_{n,1})$
is a homeomorphism. In the latter case,
$\sigma ^{j-1}: S_{n,1}\to \sigma ^{j-1}(S_{n,1})$
is a homeomorphism. In the latter case,
Primitive versus satellite renormalizations. Let
![]() $n\ge 2$
and
$n\ge 2$
and
![]() $r_n/q_n$
be the rotation number of
$r_n/q_n$
be the rotation number of
![]() $\beta _n$
. The next claim is well known; we include the proof for the reader’s convenience.
$\beta _n$
. The next claim is well known; we include the proof for the reader’s convenience.
Lemma 2.1.
-
(1) The renormalization
 $f^{p_n}$
is primitive if and only if
$f^{p_n}$
is primitive if and only if
 $r_n/q_n=0/1$
, the period of
$r_n/q_n=0/1$
, the period of
 $\beta _n$
is
$\beta _n$
is
 $p_n$
and
$p_n$
and
 $\beta _n$
is the landing point of exactly two rays and they are fixed by
$\beta _n$
is the landing point of exactly two rays and they are fixed by
 $f^{p_n}$
.
$f^{p_n}$
. -
(2) The points
 $\beta _n$
,
$\beta _n$
,
 $n=1,2,\ldots ,$
are all different.
$n=1,2,\ldots ,$
are all different. -
(3)
 $f^{p_n}$
is satellite if and only if the
$f^{p_n}$
is satellite if and only if the
 $\alpha $
-fixed point
$\alpha $
-fixed point
 $\alpha _{n-1}$
of
$\alpha _{n-1}$
of
 $f^{p_{n-1}}: f(J_{n-1})\to f(J_{n-1})$
coincides with the
$f^{p_{n-1}}: f(J_{n-1})\to f(J_{n-1})$
coincides with the
 $\beta $
-fixed point
$\beta $
-fixed point
 $\beta _n$
of
$\beta _n$
of
 $f^{p_n}:f(J_n)\to f(J_n)$
. In particular,
$f^{p_n}:f(J_n)\to f(J_n)$
. In particular,
 $\bigcup _{j=0}^{q_n-1} f^{jp_{n-1}}(f(J_n))\subset f(J_{n-1})$
and
$\bigcup _{j=0}^{q_n-1} f^{jp_{n-1}}(f(J_n))\subset f(J_{n-1})$
and
 $p_n=q_n p_{n-1}$
. Moreover, each of the
$p_n=q_n p_{n-1}$
. Moreover, each of the
 $p_{n-1}$
points of the orbit of
$p_{n-1}$
points of the orbit of
 $\beta _n$
is the landing point of precisely
$\beta _n$
is the landing point of precisely
 $q_n$
rays which are permuted by
$q_n$
rays which are permuted by
 $f^{p_{n-1}}$
according to the rotation number
$f^{p_{n-1}}$
according to the rotation number
 $r_n/q_n$
. Completed by the landing point, they split
$r_n/q_n$
. Completed by the landing point, they split
 $\mathbb {C}$
into
$\mathbb {C}$
into
 $q_n$
‘sectors’ such that the closure of each of them contains a unique ‘small’ Julia set of level n sharing a common point with the boundary of the ‘sector’.
$q_n$
‘sectors’ such that the closure of each of them contains a unique ‘small’ Julia set of level n sharing a common point with the boundary of the ‘sector’.
Proof. (1)
![]() $f^{p_n}$
is satellite if and only if
$f^{p_n}$
is satellite if and only if
![]() $f(J_n)$
meets at
$f(J_n)$
meets at
![]() $\beta _n$
some other iterate of
$\beta _n$
some other iterate of
![]() $J_n$
, hence,
$J_n$
, hence,
![]() $r_n/q_n\neq 0$
, and vice versa.
$r_n/q_n\neq 0$
, and vice versa.
(2) Assume
![]() $\beta :=\beta _n=\beta _m$
for some
$\beta :=\beta _n=\beta _m$
for some
![]() $0\le n<m$
. As
$0\le n<m$
. As
![]() $p_n<p_m$
, the period of
$p_n<p_m$
, the period of
![]() $\beta _m$
is smaller than
$\beta _m$
is smaller than
![]() $p_n$
. It follows that
$p_n$
. It follows that
![]() $f(J_n)$
contains two small Julia sets of level m that meet at
$f(J_n)$
contains two small Julia sets of level m that meet at
![]() $\beta $
, hence,
$\beta $
, hence,
![]() $\beta $
separates
$\beta $
separates
![]() $f(J_n)$
, a contradiction as
$f(J_n)$
, a contradiction as
![]() $\beta _n$
does not.
$\beta _n$
does not.
(3) By (1),
![]() $f^{p_n}$
is satellite if and only if
$f^{p_n}$
is satellite if and only if
![]() $r_n/q_n\neq 0$
. Let
$r_n/q_n\neq 0$
. Let
![]() $\tilde p_{n-1}=p_n/q_n$
. Then
$\tilde p_{n-1}=p_n/q_n$
. Then
![]() $\tilde p_{n-1}$
is an integer and is equal to the period of
$\tilde p_{n-1}$
is an integer and is equal to the period of
![]() $\beta _n$
. It follows that the
$\beta _n$
. It follows that the
![]() $p_n$
sets
$p_n$
sets
![]() $f(J_n), f^2(J_n), \ldots , f^{p_n}(J_n)$
are split into
$f(J_n), f^2(J_n), \ldots , f^{p_n}(J_n)$
are split into
![]() $\tilde p_{n-1}$
connected closed subsets
$\tilde p_{n-1}$
connected closed subsets
![]() $E_i$
,
$E_i$
,
![]() $i{\kern-1pt}={\kern-1pt}1,\ldots , \tilde { \tilde {p}}_{n-1}$
where
$i{\kern-1pt}={\kern-1pt}1,\ldots , \tilde { \tilde {p}}_{n-1}$
where
![]() $E_1{\kern-1pt}={\kern-1pt}\bigcup _{j=0}^{q_n-1} f^{j \tilde p_{n-1}}(f(J_n))$
and
$E_1{\kern-1pt}={\kern-1pt}\bigcup _{j=0}^{q_n-1} f^{j \tilde p_{n-1}}(f(J_n))$
and
![]() $E_i{\kern-1pt}={\kern-1pt}f^{i-1}(E_1)$
,
$E_i{\kern-1pt}={\kern-1pt}f^{i-1}(E_1)$
,
![]() $i=1,2,\ldots , \tilde p_{n-1}$
. Moreover,
$i=1,2,\ldots , \tilde p_{n-1}$
. Moreover,
![]() $0{\kern-1pt}\in{\kern-1pt} E_{p_{n-1}}$
and
$0{\kern-1pt}\in{\kern-1pt} E_{p_{n-1}}$
and
![]() $f(E_i){\kern-1pt}={\kern-1pt}E_{i+1}$
,
$f(E_i){\kern-1pt}={\kern-1pt}E_{i+1}$
,
![]() $i{\kern-1pt}={\kern-1pt}1,\ldots ,\tilde p_{n-1}{\kern-1pt}-{\kern-1pt}1$
,
$i{\kern-1pt}={\kern-1pt}1,\ldots ,\tilde p_{n-1}{\kern-1pt}-{\kern-1pt}1$
,
![]() $f(E_{\tilde p_{n-1}}){\kern-1pt}={\kern-1pt}E_1$
. By [Reference McMullen16, Theorem 8.5],
$f(E_{\tilde p_{n-1}}){\kern-1pt}={\kern-1pt}E_1$
. By [Reference McMullen16, Theorem 8.5],
![]() $f^{\tilde p_{n-1}}$
is a simple renormalization and the
$f^{\tilde p_{n-1}}$
is a simple renormalization and the
![]() $E_i$
,
$E_i$
,
![]() $i=1,\ldots , \tilde p_{n-1}$
, are subsets of its
$i=1,\ldots , \tilde p_{n-1}$
, are subsets of its
![]() $\tilde p_{n-1}$
small Julia sets. Since
$\tilde p_{n-1}$
small Julia sets. Since
![]() $1=p_0<p_1<\cdots $
are all consecutive periods of simple renormalizations, then
$1=p_0<p_1<\cdots $
are all consecutive periods of simple renormalizations, then
![]() $\tilde p_{n-1}=p_k$
for some
$\tilde p_{n-1}=p_k$
for some
![]() $k<n$
. Therefore, the
$k<n$
. Therefore, the
![]() $\beta _n$
-fixed point of
$\beta _n$
-fixed point of
![]() $f^{p_n}:f(J_n)\to f(J_n)$
is
$f^{p_n}:f(J_n)\to f(J_n)$
is
![]() $\alpha _k$
-fixed point of
$\alpha _k$
-fixed point of
![]() $f^{p_k}: f(J_{p_k})\to f(J_{p_k})$
. As all renormalizations are simple, if
$f^{p_k}: f(J_{p_k})\to f(J_{p_k})$
. As all renormalizations are simple, if
![]() $k<n-1$
then that would imply that
$k<n-1$
then that would imply that
![]() $\beta _n=\beta _{n-1}=\cdots =\beta _{k+1}$
, a contradiction with (2). The claim about ‘sectors’ follows since each map
$\beta _n=\beta _{n-1}=\cdots =\beta _{k+1}$
, a contradiction with (2). The claim about ‘sectors’ follows since each map
![]() $f^j$
is one-to-one in a neighborhood of
$f^j$
is one-to-one in a neighborhood of
![]() $\beta _n$
and the closure of
$\beta _n$
and the closure of
![]() $\Omega _n$
contains a single ‘small’ Julia set
$\Omega _n$
contains a single ‘small’ Julia set
![]() $f(J_n)$
of level n sharing a common point with
$f(J_n)$
of level n sharing a common point with
![]() $\partial \Omega _n$
.
$\partial \Omega _n$
.
We need a more refined estimate provided the renormalization is not doubling. Assume
![]() $f^{p_n}$
is satellite so that
$f^{p_n}$
is satellite so that
![]() $p_{n-1}=p_n/q_n$
, with
$p_{n-1}=p_n/q_n$
, with
![]() $q_n\ge 2$
, and the rotation number of
$q_n\ge 2$
, and the rotation number of
![]() $\beta _n$
is
$\beta _n$
is
![]() $r_n/q_n\neq 0/1$
.
$r_n/q_n\neq 0/1$
.
Lemma 2.2. Assume
![]() $f^{p_n}$
is satellite and
$f^{p_n}$
is satellite and
![]() $q_n=p_n/p_{n-1}\ge 3$
, that is,
$q_n=p_n/p_{n-1}\ge 3$
, that is,
![]() $f^{p_n}$
is not doubling. Then
$f^{p_n}$
is not doubling. Then
In particular, given
![]() $\zeta \in (0,1/3)$
, the length of
$\zeta \in (0,1/3)$
, the length of
![]() $\sigma ^{j-1}S_{n,1}$
tends to zero as
$\sigma ^{j-1}S_{n,1}$
tends to zero as
![]() $n\to \infty $
uniformly in
$n\to \infty $
uniformly in
![]() $j=1,\ldots , [\zeta p_n]$
(where
$j=1,\ldots , [\zeta p_n]$
(where
![]() $[x]$
is the integer part of
$[x]$
is the integer part of
![]() $x\in \mathbb {R}$
).
$x\in \mathbb {R}$
).
Moreover, for every
![]() $1\le j\le p_{n-1}(q_n-2)$
,
$1\le j\le p_{n-1}(q_n-2)$
,
![]() $S_{n,j}=\sigma ^{j-1}(S_{n,1})$
and the map
$S_{n,j}=\sigma ^{j-1}(S_{n,1})$
and the map
![]() $f^{p_n}: U_{n,j}\to \Omega _{n,j}$
is a two-to-one branched covering such that
$f^{p_n}: U_{n,j}\to \Omega _{n,j}$
is a two-to-one branched covering such that
Proof. Let
![]() $g=f^{p_{n-1}}: U_{n-1}\to \Omega _{n-1}$
. Then g is a two-to-one covering of degree
$g=f^{p_{n-1}}: U_{n-1}\to \Omega _{n-1}$
. Then g is a two-to-one covering of degree
![]() $2$
and the critical value c.
$2$
and the critical value c.
(1) Recall that
![]() $s_{n-1,1}=[t_{n-1}, t_{n-1}']\cup [\tilde t_{n-1}', \tilde t_{n-1}]$
consists of two ‘windows’ so that
$s_{n-1,1}=[t_{n-1}, t_{n-1}']\cup [\tilde t_{n-1}', \tilde t_{n-1}]$
consists of two ‘windows’ so that
![]() $\sigma ^{p_{n-1}}$
is an orientation-preserving homeomorphism of either ‘window’ onto
$\sigma ^{p_{n-1}}$
is an orientation-preserving homeomorphism of either ‘window’ onto
![]() $S_{n-1,1}=[t_{n-1}, \tilde t_{n-1}]$
.
$S_{n-1,1}=[t_{n-1}, \tilde t_{n-1}]$
.
(2) Consider the
![]() $q_n$
rays
$q_n$
rays
![]() $L_1,\ldots ,L_{q_n}$
to
$L_1,\ldots ,L_{q_n}$
to
![]() $\alpha _{n-1}$
. The map g is a local homeomorphism near
$\alpha _{n-1}$
. The map g is a local homeomorphism near
![]() $\alpha _{n-1}$
which permutes the rays to
$\alpha _{n-1}$
which permutes the rays to
![]() $\alpha _{n-1}$
according to the rotation number
$\alpha _{n-1}$
according to the rotation number
![]() $\nu :=r_n/q_n\neq 0, 1/2$
. In particular, g maps any pair of adjacent rays to
$\nu :=r_n/q_n\neq 0, 1/2$
. In particular, g maps any pair of adjacent rays to
![]() $\alpha _{n-1}$
onto another pair of adjacent rays to
$\alpha _{n-1}$
onto another pair of adjacent rays to
![]() $\alpha _{n-1}$
(see Figure 1).
$\alpha _{n-1}$
(see Figure 1).
(3) Not all arguments of these rays lie in a single ‘window’ I of
![]() $s_{n-1,1}$
because otherwise, by (1), the set of those arguments would lie in the non-escaping set of an orientation-preserving homeomorphism
$s_{n-1,1}$
because otherwise, by (1), the set of those arguments would lie in the non-escaping set of an orientation-preserving homeomorphism
![]() $\sigma ^{p_{n-1}}: I\to S_{n,1}$
, which consists of a fixed point of this map, a contradiction with the fact that
$\sigma ^{p_{n-1}}: I\to S_{n,1}$
, which consists of a fixed point of this map, a contradiction with the fact that
![]() $q_n>1$
.
$q_n>1$
.

Figure 1
![]() $q_n=3$
.
$q_n=3$
.
(4) The rays
![]() $L_j$
split
$L_j$
split
![]() $U_{n-1}$
into
$U_{n-1}$
into
![]() $q_n$
disjoint domains
$q_n$
disjoint domains
![]() $U^j$
,
$U^j$
,
![]() $j=0,1,\ldots ,q_n-1$
. By the ‘ideal boundary’
$j=0,1,\ldots ,q_n-1$
. By the ‘ideal boundary’
![]() $\hat \partial {U^j}$
of
$\hat \partial {U^j}$
of
![]() $U^j$
we will mean the usual (topological) boundary
$U^j$
we will mean the usual (topological) boundary
![]() $\partial U^j$
(in our case, the set of boundary rays completed by their landing points) along with the ‘boundary at infinity’ which is the set of arguments of rays entering
$\partial U^j$
(in our case, the set of boundary rays completed by their landing points) along with the ‘boundary at infinity’ which is the set of arguments of rays entering
![]() $U^j$
. Then define
$U^j$
. Then define
![]() $\hat g$
on
$\hat g$
on
![]() $\hat \partial {U^j}$
to be g on
$\hat \partial {U^j}$
to be g on
![]() $\partial U^j$
and
$\partial U^j$
and
![]() $\sigma ^{p_{n-1}}$
on the ‘boundary at infinity’ of
$\sigma ^{p_{n-1}}$
on the ‘boundary at infinity’ of
![]() $U^j$
.
$U^j$
.
(5) By (3), one of the
![]() $U^j$
, called
$U^j$
, called
![]() $U^0$
, has
$U^0$
, has
![]() $\beta _{n-1}$
in its boundary, and another one, called
$\beta _{n-1}$
in its boundary, and another one, called
![]() $U^{q_n-1}$
, has
$U^{q_n-1}$
, has
![]() $\beta _{n-1}'$
in its boundary. In particular, the boundary of any other
$\beta _{n-1}'$
in its boundary. In particular, the boundary of any other
![]() $U^j$
,
$U^j$
,
![]() $j{\kern-1pt}\neq{\kern-1pt} 0, q_n{\kern-1pt}-{\kern-1pt}1$
, consists of a pair of adjacent rays to
$j{\kern-1pt}\neq{\kern-1pt} 0, q_n{\kern-1pt}-{\kern-1pt}1$
, consists of a pair of adjacent rays to
![]() $\alpha _{n-1}$
whose arguments belong to a single ‘window’ of
$\alpha _{n-1}$
whose arguments belong to a single ‘window’ of
![]() $s_{n-1,1}$
. Therefore, by (1), the rest of the indices
$s_{n-1,1}$
. Therefore, by (1), the rest of the indices
![]() $j=1,\ldots , q_n-2$
can be ordered in such a way that
$j=1,\ldots , q_n-2$
can be ordered in such a way that
![]() $\hat g:\hat \partial {U^j}\to \hat \partial {U^{j+1}}$
is a one-to-one map for
$\hat g:\hat \partial {U^j}\to \hat \partial {U^{j+1}}$
is a one-to-one map for
![]() $j=1,\ldots ,q_n-3$
(note that the ‘boundary at infinity’ of each
$j=1,\ldots ,q_n-3$
(note that the ‘boundary at infinity’ of each
![]() $U^j$
,
$U^j$
,
![]() $1\le j\le q_n-2$
, consists of a single ‘arc at infinity’). Therefore,
$1\le j\le q_n-2$
, consists of a single ‘arc at infinity’). Therefore,
![]() $g: U^j\to U^{j+1}$
is a homeomorphism for
$g: U^j\to U^{j+1}$
is a homeomorphism for
![]() $j=1,\ldots , q_n-3$
. The map
$j=1,\ldots , q_n-3$
. The map
![]() $\hat g$
on
$\hat g$
on
![]() $\hat \partial {U^{q_n-2}}$
is also a one-to-one map on its image
$\hat \partial {U^{q_n-2}}$
is also a one-to-one map on its image
![]() $W=g(U^{q_n-2})$
where W is bounded by two adjacent rays to
$W=g(U^{q_n-2})$
where W is bounded by two adjacent rays to
![]() $\alpha _{n-1}$
. W cannot contain
$\alpha _{n-1}$
. W cannot contain
![]() $U^0$
because otherwise W would contain
$U^0$
because otherwise W would contain
![]() $\beta _{n-1}'$
, a contradiction. Thus W must contain
$\beta _{n-1}'$
, a contradiction. Thus W must contain
![]() $\beta _{n-1}'$
. That is,
$\beta _{n-1}'$
. That is,
![]() $g(U^{q_n-2})$
covers
$g(U^{q_n-2})$
covers
![]() $U^{q_n-1}$
.
$U^{q_n-1}$
.
Thus, for
![]() $j{\kern-1pt}={\kern-1pt}1,\ldots ,q_n{\kern-1pt}-{\kern-1pt}3$
,
$j{\kern-1pt}={\kern-1pt}1,\ldots ,q_n{\kern-1pt}-{\kern-1pt}3$
,
![]() $g: U^j{\kern-1pt}\to{\kern-1pt} U^{j+1}$
is a homeomorphism, and
$g: U^j{\kern-1pt}\to{\kern-1pt} U^{j+1}$
is a homeomorphism, and
![]() ${g: U^{q_n-2}{\kern-1pt}\to{\kern-1pt} W}$
is also a homeomorphism where the image
${g: U^{q_n-2}{\kern-1pt}\to{\kern-1pt} W}$
is also a homeomorphism where the image
![]() $W=g(U^{q_n-2})$
covers
$W=g(U^{q_n-2})$
covers
![]() $U^{q_n-1}$
and has two common rays with the boundary of
$U^{q_n-1}$
and has two common rays with the boundary of
![]() $U^{q_n-1}$
.
$U^{q_n-1}$
.
(6) The critical value c of g has a unique preimage by g (the critical point of g). As
![]() $c\in \Omega _n\subset \Omega _{n-1}$
and
$c\in \Omega _n\subset \Omega _{n-1}$
and
![]() $\Omega _n$
is bounded by two adjacent rays to
$\Omega _n$
is bounded by two adjacent rays to
![]() $\alpha _{n-1}$
,
$\alpha _{n-1}$
,
![]() $c\in U^i$
for some
$c\in U^i$
for some
![]() $i\in \{1,\ldots ,q_n-1\}$
. If
$i\in \{1,\ldots ,q_n-1\}$
. If
![]() $i>1$
, then
$i>1$
, then
![]() $i-1\ge 1$
while g would not be a homeomorphism of
$i-1\ge 1$
while g would not be a homeomorphism of
![]() $U^{i-1}$
on its image. This shows that
$U^{i-1}$
on its image. This shows that
![]() $c\in U^1=\Omega _n$
.
$c\in U^1=\Omega _n$
.
Concluding,
![]() $U^j=g^{j-1}(\Omega _n)$
,
$U^j=g^{j-1}(\Omega _n)$
,
![]() $j=1,\ldots ,q_n-2$
, in particular,
$j=1,\ldots ,q_n-2$
, in particular,
and
![]() $g^{q_n-2}:\Omega _n\to g^{q_n-2}(\Omega _n)$
is a homeomorphism, that is, (2.4) holds. It implies the rest.
$g^{q_n-2}:\Omega _n\to g^{q_n-2}(\Omega _n)$
is a homeomorphism, that is, (2.4) holds. It implies the rest.
(D) Given a compact set
![]() $Y\subset J(f)$
denote by
$Y\subset J(f)$
denote by
![]() $(\tilde Y)_f$
(or simply
$(\tilde Y)_f$
(or simply
![]() $\tilde Y$
, if the map is fixed) the set of arguments of the external rays which have their limit sets contained in Y. It follows from (C) that
$\tilde Y$
, if the map is fixed) the set of arguments of the external rays which have their limit sets contained in Y. It follows from (C) that
![]() $\tilde K_c=\bigcap _{n=1}^\infty \{ [t_n, t_n']\cup [\tilde t_n', \tilde t_n]\}$
, that is, it is either a single-point set or a two-point set.
$\tilde K_c=\bigcap _{n=1}^\infty \{ [t_n, t_n']\cup [\tilde t_n', \tilde t_n]\}$
, that is, it is either a single-point set or a two-point set.
Since
![]() $\tilde K_c$
contains at most two angles,
$\tilde K_c$
contains at most two angles,
![]() $K_c$
contains at most two different accessible points. More generally, given
$K_c$
contains at most two different accessible points. More generally, given
![]() $x\in J^{\prime }_\infty $
, let
$x\in J^{\prime }_\infty $
, let
Then
![]() $s_{n+1,j_{n+1}(x)}\subset s_{n,j_{n}(x)}$
so that
$s_{n+1,j_{n+1}(x)}\subset s_{n,j_{n}(x)}$
so that
is not empty and consists of either one or two components. Since
![]() $p_n-j_n(x)\to \infty $
for
$p_n-j_n(x)\to \infty $
for
![]() $x\in J^{\prime }_\infty $
we conclude using (2.1), that
$x\in J^{\prime }_\infty $
we conclude using (2.1), that
![]() $s_{\infty , x}$
consists of either a single point or two different points. In particular, for any component K of
$s_{\infty , x}$
consists of either a single point or two different points. In particular, for any component K of
![]() $J_\infty $
which is not one of
$J_\infty $
which is not one of
![]() $f^{-j}(K_0)$
,
$f^{-j}(K_0)$
,
![]() $j\ge 0$
, there are either one or two rays tending to K.
$j\ge 0$
, there are either one or two rays tending to K.
From now on,
![]() $\mu $
is an f-invariant probability ergodic measure supported in
$\mu $
is an f-invariant probability ergodic measure supported in
![]() $J_\infty $
:
$J_\infty $
:
![]() $\operatorname {\mathrm {supp}} \mu \subset J_\infty $
, and having a positive Lyapunov exponent
$\operatorname {\mathrm {supp}} \mu \subset J_\infty $
, and having a positive Lyapunov exponent
(E). We start with the following basic statement. Parts (i)–(ii) are easy consequences of the invariance of
![]() $\mu $
and (B), while (iii) is a part of Pesin’s theory as in [Reference Przytycki and Urbański25, Theorem 11.2.3] coupled with the structure of
$\mu $
and (B), while (iii) is a part of Pesin’s theory as in [Reference Przytycki and Urbański25, Theorem 11.2.3] coupled with the structure of
![]() $f:J_\infty \to J_\infty $
(see (B)). Recall that
$f:J_\infty \to J_\infty $
(see (B)). Recall that
![]() $J_\infty '=J_\infty \setminus \bigcup _{j=-\infty }^{\infty } f^j(K_0)$
.
$J_\infty '=J_\infty \setminus \bigcup _{j=-\infty }^{\infty } f^j(K_0)$
.
Proposition 2.3.
-
(i) For every n and
 $0\le j<p_n$
,
$0\le j<p_n$
,
 $\mu (f^j(J_n))=1/p_n$
.
$\mu (f^j(J_n))=1/p_n$
. -
(ii)
 $\mu $
has no atoms and
$\mu $
has no atoms and
 $\mu (K)=0$
for every component K of
$\mu (K)=0$
for every component K of
 $J_\infty $
.
$J_\infty $
. -
(iii)
 $\mu (J_\infty ')=1$
and
$\mu (J_\infty ')=1$
and
 $f: J_\infty '\to J_\infty '$
is a
$f: J_\infty '\to J_\infty '$
is a
 $\mu $
-measure preserving homeomorphism.
$\mu $
-measure preserving homeomorphism.
There exists a measurable positive function
![]() $\tilde r(x)>0$
on
$\tilde r(x)>0$
on
![]() $J_\infty '$
such that for
$J_\infty '$
such that for
![]() $\mu $
-almost every
$\mu $
-almost every
![]() $x\in J_\infty '$
, and all
$x\in J_\infty '$
, and all
![]() $n\in \mathbb {N}$
, if
$n\in \mathbb {N}$
, if
![]() $x_{-n}$
is the unique point of
$x_{-n}$
is the unique point of
![]() $J_\infty '$
with
$J_\infty '$
with
![]() $f^n(x_{-n})=x$
, then a (univalent) branch
$f^n(x_{-n})=x$
, then a (univalent) branch
![]() $g_n: B(x, \tilde r(x))\to \mathbb {C}$
of
$g_n: B(x, \tilde r(x))\to \mathbb {C}$
of
![]() $f^{-n}$
is well defined such that
$f^{-n}$
is well defined such that
![]() $g_n(x)=x_{-n}$
,
$g_n(x)=x_{-n}$
,
Remark 2.4. The branch
![]() $g_n$
of
$g_n$
of
![]() $f^{-n}$
depends on n and
$f^{-n}$
depends on n and
![]() $x_{-n}$
but it should be clear from the context which points x and
$x_{-n}$
but it should be clear from the context which points x and
![]() $x_{-n}$
are meant.
$x_{-n}$
are meant.
Using Birkhoff’s ergodic theorem and Egorov’s theorem, Proposition 2.3 immediately implies (
![]() $\mathrm {e}_1$
)–(
$\mathrm {e}_1$
)–(
![]() $\mathrm {e}_3$
) of the next corollary. The proof of (
$\mathrm {e}_3$
) of the next corollary. The proof of (
![]() $\mathrm {e}_4$
)–(
$\mathrm {e}_4$
)–(
![]() $\mathrm {e}_5$
) is given immediately after the result.
$\mathrm {e}_5$
) is given immediately after the result.
Corollary 2.5. For every
![]() $\epsilon>0$
, there exist a closed set
$\epsilon>0$
, there exist a closed set
![]() $E^{\prime }_{\epsilon /2}\subset J_\infty '$
and constants
$E^{\prime }_{\epsilon /2}\subset J_\infty '$
and constants
![]() $\rho =\rho (\epsilon )>0$
,
$\rho =\rho (\epsilon )>0$
,
![]() $\kappa =\kappa (\epsilon )\in (0,1)$
such that the following statements hold.
$\kappa =\kappa (\epsilon )\in (0,1)$
such that the following statements hold.
-
(e1)
 $\mu (E^{\prime }_{\epsilon /2})>1-{\epsilon }/{2}$
.
$\mu (E^{\prime }_{\epsilon /2})>1-{\epsilon }/{2}$
. -
(e2) There exists another closed set
 $\hat E_{\epsilon /2}$
such that
$\hat E_{\epsilon /2}$
such that
 $E^{\prime }_{\epsilon /2}\subset \hat E_{\epsilon /2}\subset J^{\prime }_\infty $
as follows. For every
$E^{\prime }_{\epsilon /2}\subset \hat E_{\epsilon /2}\subset J^{\prime }_\infty $
as follows. For every
 $x{\kern-1pt}\in{\kern-1pt} \hat E_{\epsilon /2}$
and every
$x{\kern-1pt}\in{\kern-1pt} \hat E_{\epsilon /2}$
and every
 $m{\kern-1pt}>{\kern-1pt}0$
there exists a (univalent) branch
$m{\kern-1pt}>{\kern-1pt}0$
there exists a (univalent) branch
 $g_m{\kern-1pt}:{\kern-1pt} B(x, 3\rho ){\kern-1pt}\to{\kern-1pt} \mathbb {C}$
of
$g_m{\kern-1pt}:{\kern-1pt} B(x, 3\rho ){\kern-1pt}\to{\kern-1pt} \mathbb {C}$
of
 $f^{-m}$
such that
$f^{-m}$
such that
 $g_m(x)=x_{-m}$
and
$g_m(x)=x_{-m}$
and
 $|g^{\prime }_m(x_1)/g^{\prime }_m(x_2)|<2$
, for every
$|g^{\prime }_m(x_1)/g^{\prime }_m(x_2)|<2$
, for every
 $x_1, x_2\in B(x,2\rho )$
. Moreover,
$x_1, x_2\in B(x,2\rho )$
. Moreover,
 $m^{-1}\ln |g^{\prime }_m(x)|\to -\chi (\mu )$
as
$m^{-1}\ln |g^{\prime }_m(x)|\to -\chi (\mu )$
as
 $m\to \infty $
uniformly in
$m\to \infty $
uniformly in
 $x\in E^{\prime }_{\epsilon /2}$
.
$x\in E^{\prime }_{\epsilon /2}$
. -
(e3) For every
 $x\in E^{\prime }_{\epsilon /2}$
there exists a sequence of positive integers
$x\in E^{\prime }_{\epsilon /2}$
there exists a sequence of positive integers
 $n_j=n_j(x)$
,
$n_j=n_j(x)$
,
 $j=1,2,\ldots ,$
such that
$j=1,2,\ldots ,$
such that
 $j/n_j\ge \kappa $
and
$j/n_j\ge \kappa $
and
 $f^{n_j}(x)\in \hat E_{\epsilon /2}$
for all j.
$f^{n_j}(x)\in \hat E_{\epsilon /2}$
for all j. -
(e4) Given
 $x\in J_\infty $
and
$x\in J_\infty $
and
 $n\ge 0$
, let
$n\ge 0$
, let
 $j_n(x)$
be the unique
$j_n(x)$
be the unique
 $1\le j< p_n$
such that
$1\le j< p_n$
such that
 $x\in f^j(J_n)$
. Then
$x\in f^j(J_n)$
. Then
 $p_n-j_n(x)\to \infty $
as
$p_n-j_n(x)\to \infty $
as
 $n\to \infty $
uniformly in
$n\to \infty $
uniformly in
 $x\in E^{\prime }_{\epsilon /2}$
.
$x\in E^{\prime }_{\epsilon /2}$
. -
(e5) For
 $s_{n,j_n(x)}=[t_{n,j_n(x)}, t_{n,j_n(x)}']\cup [\tilde t_{n,j_n(x)}', \tilde t_{n,j_n(x)}]$
, we have
$s_{n,j_n(x)}=[t_{n,j_n(x)}, t_{n,j_n(x)}']\cup [\tilde t_{n,j_n(x)}', \tilde t_{n,j_n(x)}]$
, we have
 $s_{n+1,j_{n+1}(x)}\subset s_{n,j_{n}(x)}$
and as
$s_{n+1,j_{n+1}(x)}\subset s_{n,j_{n}(x)}$
and as $$ \begin{align*}|t_{n,j_n(x)}-t_{n,j_n(x)}'|=|\tilde t_{n,j_n(x)}'-\tilde t_{n,j_n(x)}|\to 0\end{align*} $$
$$ \begin{align*}|t_{n,j_n(x)}-t_{n,j_n(x)}'|=|\tilde t_{n,j_n(x)}'-\tilde t_{n,j_n(x)}|\to 0\end{align*} $$
 $n\to \infty $
uniformly in
$n\to \infty $
uniformly in
 $x\in E^{\prime }_{\epsilon /2}$
.
$x\in E^{\prime }_{\epsilon /2}$
.
Proof of (
![]() $\mathrm {e}_4$
)–(
$\mathrm {e}_4$
)–(
![]() $\mathrm {e}_5$
). Assuming the contrary in (
$\mathrm {e}_5$
). Assuming the contrary in (
![]() $\mathrm {e}_4$
), we find some N and sequences
$\mathrm {e}_4$
), we find some N and sequences
![]() $(n_k){\kern-1pt}\subset{\kern-1pt} \mathbb {N}$
and
$(n_k){\kern-1pt}\subset{\kern-1pt} \mathbb {N}$
and
![]() $(x_k)$
,
$(x_k)$
,
![]() $x_k{\kern-1pt}\in{\kern-1pt} E^{\prime }_{\epsilon /2}$
, such that
$x_k{\kern-1pt}\in{\kern-1pt} E^{\prime }_{\epsilon /2}$
, such that
![]() $p_{n_k}{\kern-1pt}-{\kern-1pt}j_{n_k}(x_k){\kern-1pt}={\kern-1pt}N$
(see (B)), hence
$p_{n_k}{\kern-1pt}-{\kern-1pt}j_{n_k}(x_k){\kern-1pt}={\kern-1pt}N$
(see (B)), hence
![]() $x_k{\kern-1pt}\in{\kern-1pt} f^{-N}(J_{n_k})$
, for all k. Since
$x_k{\kern-1pt}\in{\kern-1pt} f^{-N}(J_{n_k})$
, for all k. Since
![]() $E_{\epsilon /2}$
is closed, one can assume
$E_{\epsilon /2}$
is closed, one can assume
![]() $x_k\to x\in E^{\prime }_{\epsilon /2}\subset J^{\prime }_\infty $
. Hence,
$x_k\to x\in E^{\prime }_{\epsilon /2}\subset J^{\prime }_\infty $
. Hence,
![]() $x\in f^{-N}(K_0)$
, a contradiction. Now for (
$x\in f^{-N}(K_0)$
, a contradiction. Now for (
![]() $\mathrm {e}_5$
), using (
$\mathrm {e}_5$
), using (
![]() $\mathrm {e}_4$
),
$\mathrm {e}_4$
),
![]() $t_{n,j_n(x)}' - t_{n,j_n(x)} = \tilde t_{n,j_n(x)} - \tilde t_{n,j_n(x)}'<{1}/{2^{p_{n}-j_n(x)}}\to 0$
uniformly in x.
$t_{n,j_n(x)}' - t_{n,j_n(x)} = \tilde t_{n,j_n(x)} - \tilde t_{n,j_n(x)}'<{1}/{2^{p_{n}-j_n(x)}}\to 0$
uniformly in x.
3. External rays to typical points
We define a telescope essentially following [Reference Przytycki23]. Given
![]() $x\in J(f)$
,
$x\in J(f)$
,
![]() $r>0$
,
$r>0$
,
![]() $\delta>0$
,
$\delta>0$
,
![]() $k\in \mathbb {N}$
and
$k\in \mathbb {N}$
and
![]() $\kappa {\kern-1pt}\in{\kern-1pt} (0,1)$
, an
$\kappa {\kern-1pt}\in{\kern-1pt} (0,1)$
, an
![]() $(r, \kappa , \delta , k)$
-telescope at
$(r, \kappa , \delta , k)$
-telescope at
![]() $x\in J$
is a collection of times
$x\in J$
is a collection of times
![]() $0{\kern-1pt}={\kern-1pt}n_0{\kern-1pt}<{\kern-1pt}n_1{\kern-1pt}<{\kern-1pt}\cdots {\kern-1pt}<{\kern-1pt}n_k$
and disks
$0{\kern-1pt}={\kern-1pt}n_0{\kern-1pt}<{\kern-1pt}n_1{\kern-1pt}<{\kern-1pt}\cdots {\kern-1pt}<{\kern-1pt}n_k$
and disks
![]() $B_l=B(f^{n_l}(x), r)$
,
$B_l=B(f^{n_l}(x), r)$
,
![]() $l=0,1,\ldots ,k$
, such that, for every
$l=0,1,\ldots ,k$
, such that, for every
![]() $l>0$
: (i)
$l>0$
: (i)
![]() $l/n_l>\kappa $
; (ii) there is a univalent branch
$l/n_l>\kappa $
; (ii) there is a univalent branch
![]() $g_{n_l}: B(f^{n_l}(x), 2r)\to \mathbb {C}$
of
$g_{n_l}: B(f^{n_l}(x), 2r)\to \mathbb {C}$
of
![]() $f^{-n_l}$
so that
$f^{-n_l}$
so that
![]() $g_{n_l}(f^{n_l}(x))=x$
and, for
$g_{n_l}(f^{n_l}(x))=x$
and, for
![]() $l=1,\ldots ,k$
,
$l=1,\ldots ,k$
,
![]() $d(f^{n_{l-1}}\circ g_{n_l}(B_l), \partial B_{l-1})>\delta $
(clearly, here
$d(f^{n_{l-1}}\circ g_{n_l}(B_l), \partial B_{l-1})>\delta $
(clearly, here
![]() $f^{n_{l-1}}\circ g_{n_l}$
is a branch of
$f^{n_{l-1}}\circ g_{n_l}$
is a branch of
![]() $f^{-(n_l-n_{l-1})}$
that maps
$f^{-(n_l-n_{l-1})}$
that maps
![]() $f^{n_l}(x)$
to
$f^{n_l}(x)$
to
![]() $f^{n_{l-1}}(x)$
). The trace of the telescope is a collection of sets
$f^{n_{l-1}}(x)$
). The trace of the telescope is a collection of sets
![]() $B_{l,0}=g_{n_l}(B_l)$
,
$B_{l,0}=g_{n_l}(B_l)$
,
![]() $l=0,1,\ldots ,k$
. We have
$l=0,1,\ldots ,k$
. We have
![]() $B_{k,0}\subset B_{k-1,0}\subset \cdots \subset B_{1,0}\subset B_{0,0}=B_0=B(x,r)$
.
$B_{k,0}\subset B_{k-1,0}\subset \cdots \subset B_{1,0}\subset B_{0,0}=B_0=B(x,r)$
.
By the first point of intersection of a ray
![]() $R_t$
, or an arc of
$R_t$
, or an arc of
![]() $R_t$
, with a set E we mean a point of
$R_t$
, with a set E we mean a point of
![]() $R_t\cap E$
with the minimal level (if it exists).
$R_t\cap E$
with the minimal level (if it exists).
Theorem 3.1. [Reference Przytycki23]
Given
![]() $r{\kern-1pt}>{\kern-1pt}0$
,
$r{\kern-1pt}>{\kern-1pt}0$
,
![]() $\kappa {\kern-1pt}\in{\kern-1pt} (0,1)$
,
$\kappa {\kern-1pt}\in{\kern-1pt} (0,1)$
,
![]() $\delta{\kern-1pt}>{\kern-1pt}0$
and
$\delta{\kern-1pt}>{\kern-1pt}0$
and
![]() $C{\kern-1pt}>{\kern-1pt}0$
, there exist
$C{\kern-1pt}>{\kern-1pt}0$
, there exist
![]() $M{\kern-1pt}>{\kern-1pt}0$
,
$M{\kern-1pt}>{\kern-1pt}0$
,
![]() $\tilde l,\tilde k\in \mathbb {N}$
and
$\tilde l,\tilde k\in \mathbb {N}$
and
![]() $K>1$
such that for every
$K>1$
such that for every
![]() $(r, \kappa , \delta , k)$
-telescope the following statements hold. Let
$(r, \kappa , \delta , k)$
-telescope the following statements hold. Let
![]() $k>\tilde k$
. Let
$k>\tilde k$
. Let
![]() $u_0=u$
be any point at the boundary of
$u_0=u$
be any point at the boundary of
![]() $B_k$
such that
$B_k$
such that
![]() $G(u)\ge C$
. Then there are indexes
$G(u)\ge C$
. Then there are indexes
![]() $1\le l_1<l_2<\cdots <l_j=k$
such that
$1\le l_1<l_2<\cdots <l_j=k$
such that
![]() $l_1<\tilde l$
,
$l_1<\tilde l$
,
![]() $l_{i+1}<K l_i$
,
$l_{i+1}<K l_i$
,
![]() $i=1,\ldots ,j-1$
, as follows. Let
$i=1,\ldots ,j-1$
, as follows. Let
![]() $u_k=g_{n_k}(u)\in \partial B_{k,0}$
and let
$u_k=g_{n_k}(u)\in \partial B_{k,0}$
and let
![]() $\gamma _k$
be an infinite arc of an external ray through
$\gamma _k$
be an infinite arc of an external ray through
![]() $u_k$
between the point
$u_k$
between the point
![]() $u_k$
and
$u_k$
and
![]() $\infty $
. Let
$\infty $
. Let
![]() $u_{k,k}=u_k$
and, for
$u_{k,k}=u_k$
and, for
![]() $l=1,\ldots ,k-1$
, let
$l=1,\ldots ,k-1$
, let
![]() $u_{k,l}$
be the first point of intersection of
$u_{k,l}$
be the first point of intersection of
![]() $\gamma _k$
with
$\gamma _k$
with
![]() $\partial B_{l,0}$
. Then, for
$\partial B_{l,0}$
. Then, for
![]() $i=1,\ldots ,j$
,
$i=1,\ldots ,j$
,
The next proposition, a corollary of Theorem 3.1, is a key one.
Proposition 3.1. Given
![]() $\epsilon>0$
, there exists a closed set
$\epsilon>0$
, there exists a closed set
![]() $E_\epsilon $
as follows. First,
$E_\epsilon $
as follows. First,
![]() $\mu (E_\epsilon )>1-\epsilon $
and
$\mu (E_\epsilon )>1-\epsilon $
and
![]() $E_\epsilon \subset E^{\prime }_{\epsilon /2}$
, where
$E_\epsilon \subset E^{\prime }_{\epsilon /2}$
, where
![]() $E^{\prime }_{\epsilon /2}$
is the set defined in (E) and satisfies (
$E^{\prime }_{\epsilon /2}$
is the set defined in (E) and satisfies (
![]() $\mathrm {e}_1$
)–(
$\mathrm {e}_1$
)–(
![]() $\mathrm {e}_5$
). There exists
$\mathrm {e}_5$
). There exists
![]() $r=r(\epsilon )>0$
and, for each
$r=r(\epsilon )>0$
and, for each
![]() $\nu>0$
, there is
$\nu>0$
, there is
![]() $C(\nu )>0$
as follows.
$C(\nu )>0$
as follows.
-
(1) Let
 $x\in E_\epsilon $
. Then x is the landing point of an external ray
$x\in E_\epsilon $
. Then x is the landing point of an external ray
 $R_{t(x)}$
of the argument
$R_{t(x)}$
of the argument
 $t(x)$
. Moreover, the first intersection of
$t(x)$
. Moreover, the first intersection of
 $R_{t(x)}$
with
$R_{t(x)}$
with
 $\partial B(x,\nu )$
has level at least
$\partial B(x,\nu )$
has level at least
 $C(\nu )$
.
$C(\nu )$
. -
(2) For each n, a branch
 $g_n: B(x,2r)\to \mathbb {C}$
of
$g_n: B(x,2r)\to \mathbb {C}$
of
 $f^{-n}$
is well defined such that
$f^{-n}$
is well defined such that
 $g_n(x)=x_{-n}$
,
$g_n(x)=x_{-n}$
,
 $|g^{\prime }_n(x_1)/g^{\prime }_n(x_2)|<2$
, for every
$|g^{\prime }_n(x_1)/g^{\prime }_n(x_2)|<2$
, for every
 $x_1, x_2\in B(x,r)$
and
$x_1, x_2\in B(x,r)$
and
 $n^{-1}\ln |g^{\prime }_n(x)|\to -\chi (\mu )$
as
$n^{-1}\ln |g^{\prime }_n(x)|\to -\chi (\mu )$
as
 $m\to \infty $
uniformly in
$m\to \infty $
uniformly in
 $x\in E_\epsilon $
.
$x\in E_\epsilon $
. -
(3) If
 $x'=g_n(x)\in E_\epsilon $
, then
$x'=g_n(x)\in E_\epsilon $
, then
 $f^n(R_{t(x')})=R_{t(x)}$
.
$f^n(R_{t(x')})=R_{t(x)}$
.
Proof. Statements (1)–(2) will hold already for the set
![]() $E^{\prime }_{\epsilon /2}$
which follows from Theorem 3.1 as in [Reference Przytycki23] and uses only the fact that
$E^{\prime }_{\epsilon /2}$
which follows from Theorem 3.1 as in [Reference Przytycki23] and uses only the fact that
![]() $\mu $
has a positive exponent; (3) will follow in our case as we shrink the set
$\mu $
has a positive exponent; (3) will follow in our case as we shrink the set
![]() $E^{\prime }_{\epsilon /2}$
a bit since each point
$E^{\prime }_{\epsilon /2}$
a bit since each point
![]() $x\in J_\infty '$
admits at most two external arguments.
$x\in J_\infty '$
admits at most two external arguments.
Here are details. Let
![]() $r=\rho (\epsilon )$
and
$r=\rho (\epsilon )$
and
![]() $\kappa =\kappa (\epsilon )$
as in the properties (
$\kappa =\kappa (\epsilon )$
as in the properties (
![]() $\mathrm {e}_2$
)–(
$\mathrm {e}_2$
)–(
![]() $\mathrm {e}_3$
) of the set
$\mathrm {e}_3$
) of the set
![]() $E^{\prime }_{\epsilon /2}$
. Then, by (
$E^{\prime }_{\epsilon /2}$
. Then, by (
![]() $\mathrm {e}_2$
)–(
$\mathrm {e}_2$
)–(
![]() $\mathrm {e}_3$
), there is
$\mathrm {e}_3$
), there is
![]() $\delta>0$
such that, for each k, every
$\delta>0$
such that, for each k, every
![]() $x\in E^{\prime }_{\epsilon /2}$
admits an
$x\in E^{\prime }_{\epsilon /2}$
admits an
![]() $(r, \kappa , \delta , k)$
-telescope with the times
$(r, \kappa , \delta , k)$
-telescope with the times
![]() $0=n_0<n_1<n_2<\cdots <n_k$
that appear in property (
$0=n_0<n_1<n_2<\cdots <n_k$
that appear in property (
![]() $\mathrm {e}_3$
) of
$\mathrm {e}_3$
) of
![]() $E^{\prime }_{\epsilon /2}$
. On the other hand, there exists
$E^{\prime }_{\epsilon /2}$
. On the other hand, there exists
![]() $L_r>0$
such that for every
$L_r>0$
such that for every
![]() $z\in J(f)$
there is a point
$z\in J(f)$
there is a point
![]() $u(z)\in \partial B(z,r)$
with the level
$u(z)\in \partial B(z,r)$
with the level
![]() $G(u(z))>L_r$
. This is so due to
$G(u(z))>L_r$
. This is so due to
![]() $\bigcup _{L>0}\{G(z)\ge L\}= A_\infty $
. Given this
$\bigcup _{L>0}\{G(z)\ge L\}= A_\infty $
. Given this
![]() $C=L_r$
, let M,
$C=L_r$
, let M,
![]() $\tilde l$
and
$\tilde l$
and
![]() $\tilde k$
be as in Theorem 3.1.
$\tilde k$
be as in Theorem 3.1.
Let
![]() $x\in E^{\prime }_{\epsilon /2}$
and
$x\in E^{\prime }_{\epsilon /2}$
and
![]() $n_1<n_2<\cdots <n_k<\cdots $
as in (
$n_1<n_2<\cdots <n_k<\cdots $
as in (
![]() $\mathrm {e}_3$
). Fix
$\mathrm {e}_3$
). Fix
![]() $k>\tilde k$
. Let
$k>\tilde k$
. Let
![]() $B_{k,0}(x)\subset B_{k-1,0}(x)\subset \cdots \subset B_{1,0}(x)\subset B_{0,0}(x)$
be the corresponding trace. By Theorem 3.1, there are
$B_{k,0}(x)\subset B_{k-1,0}(x)\subset \cdots \subset B_{1,0}(x)\subset B_{0,0}(x)$
be the corresponding trace. By Theorem 3.1, there are
![]() $1\le l_{1,k}(x)<l_{2,k}(x)<\cdots <l_{j^x_k,k}(x)=k$
such that
$1\le l_{1,k}(x)<l_{2,k}(x)<\cdots <l_{j^x_k,k}(x)=k$
such that
![]() $l_{1,k}(x)<\tilde l$
,
$l_{1,k}(x)<\tilde l$
,
![]() $l_{i+1,k}(x)<K l_{i,k}(x)$
,
$l_{i+1,k}(x)<K l_{i,k}(x)$
,
![]() $i=1,\ldots ,j^x_k-1$
. Let
$i=1,\ldots ,j^x_k-1$
. Let
![]() $\gamma _k(x)$
be an arc of an external ray between the point
$\gamma _k(x)$
be an arc of an external ray between the point
![]() $u_k(x):=g_{n_k}(u(f^{n_k}(x))$
and
$u_k(x):=g_{n_k}(u(f^{n_k}(x))$
and
![]() $\infty $
. Let
$\infty $
. Let
![]() $u_{k,l}(x)$
be the first intersection of
$u_{k,l}(x)$
be the first intersection of
![]() $\gamma _k(x)$
with
$\gamma _k(x)$
with
![]() $\partial B_{l,0}(x)$
. Then, for
$\partial B_{l,0}(x)$
. Then, for
![]() $i=1,\ldots ,j^x_k-1$
,
$i=1,\ldots ,j^x_k-1$
,
For all
![]() $i=1,\ldots ,j^x_k-1$
,
$i=1,\ldots ,j^x_k-1$
,
Denote by
![]() $t_k(x)$
the argument of an external ray that contains the arc
$t_k(x)$
the argument of an external ray that contains the arc
![]() $\gamma _k(x)$
.
$\gamma _k(x)$
.
Now, given a sequence
such that
![]() $k_1>\tilde k$
, we get a sequence of arguments
$k_1>\tilde k$
, we get a sequence of arguments
![]() $t_{k_m}(x)$
and a sequence of arcs
$t_{k_m}(x)$
and a sequence of arcs
![]() $\gamma _{k_m}(x)$
of external rays of the corresponding arguments
$\gamma _{k_m}(x)$
of external rays of the corresponding arguments
![]() $t_{k_m}(x)$
. Passing to a subsequence in the sequence
$t_{k_m}(x)$
. Passing to a subsequence in the sequence
![]() $(k_m)$
, if necessary, one can assume that
$(k_m)$
, if necessary, one can assume that
![]() $t_{k_m}(x)\to \tilde t(x)$
, for some argument
$t_{k_m}(x)\to \tilde t(x)$
, for some argument
![]() $\tilde t(x)$
.
$\tilde t(x)$
.
Fix any
![]() $\nu \in (0,r)$
and choose
$\nu \in (0,r)$
and choose
![]() $\tilde k_0>\tilde k$
such that
$\tilde k_0>\tilde k$
such that
and let
Then, by Theorem 3.1, for each
![]() $k_m>k_0$
, the first intersection of the ray
$k_m>k_0$
, the first intersection of the ray
![]() $R_{t_{k_m}}(x)$
with the boundary of
$R_{t_{k_m}}(x)$
with the boundary of
![]() $B(x,\nu )$
has level at least
$B(x,\nu )$
has level at least
![]() $C(\nu )$
. It follows, for any
$C(\nu )$
. It follows, for any
![]() $0<C<C(\nu )$
, that the sequence of arcs of the rays
$0<C<C(\nu )$
, that the sequence of arcs of the rays
![]() $R_{t_{k_m}(x)}$
between the levels C and
$R_{t_{k_m}(x)}$
between the levels C and
![]() $C(\nu )$
does not exit
$C(\nu )$
does not exit
![]() $B(x,\nu )$
for all
$B(x,\nu )$
for all
![]() $k_m>k_0$
. As
$k_m>k_0$
. As
![]() $t_{k_m}(x)\to \tilde t(x)$
, it follows that the arc of the ray
$t_{k_m}(x)\to \tilde t(x)$
, it follows that the arc of the ray
![]() $R_{\tilde t(x)}$
between levels C and
$R_{\tilde t(x)}$
between levels C and
![]() $C(\nu )$
stays in
$C(\nu )$
stays in
![]() $B(x,\nu )$
too. As
$B(x,\nu )$
too. As
![]() $\nu>0$
and
$\nu>0$
and
![]() $C\in (0, C(\nu ))$
can be chosen arbitrary small,
$C\in (0, C(\nu ))$
can be chosen arbitrary small,
![]() $R_{\tilde t(x)}$
must land at x and satisfy (1) with
$R_{\tilde t(x)}$
must land at x and satisfy (1) with
![]() $t(x)$
replaced by
$t(x)$
replaced by
![]() $\tilde t(x)$
.
$\tilde t(x)$
.
Let us call the above procedure of getting
![]() $\tilde t(x)$
from the constants r,
$\tilde t(x)$
from the constants r,
![]() $L_r$
, the point
$L_r$
, the point
![]() $x\in E^{\prime }_{\epsilon /2}$
, and the sequence (3.3) the
$x\in E^{\prime }_{\epsilon /2}$
, and the sequence (3.3) the
![]() $(r, L_r, x, (k_m))$
-procedure.
$(r, L_r, x, (k_m))$
-procedure.
Note that (2) is property (
![]() $\mathrm {e}_2$
) of the set
$\mathrm {e}_2$
) of the set
![]() $E^{\prime }_{\epsilon /2}$
.
$E^{\prime }_{\epsilon /2}$
.
In order to satisfy property (3), we shrink the set
![]() $E^{\prime }_{\epsilon /2}$
and correct
$E^{\prime }_{\epsilon /2}$
and correct
![]() $\tilde t(x)$
, changing it to some
$\tilde t(x)$
, changing it to some
![]() $t(x)$
(if necessary) as follows. Using Birkhoff’s ergodic theorem and Egorov’s theorem, choose a closed subset
$t(x)$
(if necessary) as follows. Using Birkhoff’s ergodic theorem and Egorov’s theorem, choose a closed subset
![]() $E_\epsilon $
of
$E_\epsilon $
of
![]() $E^{\prime }_{\epsilon /2}$
such that
$E^{\prime }_{\epsilon /2}$
such that
![]() $\mu (E_\epsilon )>1-\epsilon $
and, for each
$\mu (E_\epsilon )>1-\epsilon $
and, for each
![]() $x\in E_\epsilon $
, the set
$x\in E_\epsilon $
, the set
![]() $\mathcal {N}(x):=\{N\in \mathbb {N}: f^N(x)\in E^{\prime }_{\epsilon /2}\}$
is infinite. Note that
$\mathcal {N}(x):=\{N\in \mathbb {N}: f^N(x)\in E^{\prime }_{\epsilon /2}\}$
is infinite. Note that
![]() $\mathcal {N}(x)\subset \{n_k\}_{k=1}^\infty $
. We have proved that, for each
$\mathcal {N}(x)\subset \{n_k\}_{k=1}^\infty $
. We have proved that, for each
![]() $N\in \mathcal {N}(x)$
, (1) holds for the point
$N\in \mathcal {N}(x)$
, (1) holds for the point
![]() $f^N(x)$
instead of x; in particular,
$f^N(x)$
instead of x; in particular,
![]() $\tilde t(f^N(x))$
is an argument of
$\tilde t(f^N(x))$
is an argument of
![]() $f^N(x)$
. On the other hand, by (D), each
$f^N(x)$
. On the other hand, by (D), each
![]() $y\in E_\epsilon $
admits at most two external arguments, hence, all possible external arguments of the forward orbit
$y\in E_\epsilon $
admits at most two external arguments, hence, all possible external arguments of the forward orbit
![]() $f^n(x)$
,
$f^n(x)$
,
![]() $n\ge 0$
, belong to at most two different orbits of
$n\ge 0$
, belong to at most two different orbits of
![]() $\sigma : S^1\to S^1$
. Hence, there is one of those orbits,
$\sigma : S^1\to S^1$
. Hence, there is one of those orbits,
![]() $O=\{\sigma ^n(t(x))\}_{n\ge 0}$
for some
$O=\{\sigma ^n(t(x))\}_{n\ge 0}$
for some
![]() $t(x)$
, such that the intersection
$t(x)$
, such that the intersection
![]() $O\cap \{\tilde t(f^N(x)): N\in \mathcal {N}(x)\}$
is an infinite set, so that
$O\cap \{\tilde t(f^N(x)): N\in \mathcal {N}(x)\}$
is an infinite set, so that
![]() $\tilde t(f^{n_{k_m(x)}}(x))=\sigma ^{n_{k_m(x)}}(t(x))$
for an infinite sequence
$\tilde t(f^{n_{k_m(x)}}(x))=\sigma ^{n_{k_m(x)}}(t(x))$
for an infinite sequence
![]() $(k_m(x))_{m\ge 1}$
.
$(k_m(x))_{m\ge 1}$
.
Let us start over with the
![]() $(r/2, C(r/2), x, (k_m(x)))$
-procedure for the point x and the sequence
$(r/2, C(r/2), x, (k_m(x)))$
-procedure for the point x and the sequence
![]() $\{k_j(x)\}$
. Then, by construction,
$\{k_j(x)\}$
. Then, by construction,
![]() $t_{k_m(x)}=t(x)$
for all m, hence (1) holds with
$t_{k_m(x)}=t(x)$
for all m, hence (1) holds with
![]() $t(x)$
instead of the previous
$t(x)$
instead of the previous
![]() $\tilde t(x)$
. If
$\tilde t(x)$
. If
![]() $y\in E_\epsilon $
is any other point of the grand orbit
$y\in E_\epsilon $
is any other point of the grand orbit
![]() $\{f^n(x): n\in \mathbb {Z}\}$
(remember that
$\{f^n(x): n\in \mathbb {Z}\}$
(remember that
![]() $f:J^{\prime }_\infty \to J^{\prime }_\infty $
is invertible), the
$f:J^{\prime }_\infty \to J^{\prime }_\infty $
is invertible), the
![]() $(r/2, C(r/2), y, (k_m))$
-procedure works for y with the same (perhaps, truncated) sequence
$(r/2, C(r/2), y, (k_m))$
-procedure works for y with the same (perhaps, truncated) sequence
![]() $k_1(x)<k_2(x)<\cdots $
, which ensures that (3) holds (for the corrected arguments) too.
$k_1(x)<k_2(x)<\cdots $
, which ensures that (3) holds (for the corrected arguments) too.
Remark 3.2. Given
![]() $t(x)$
, we cannot just set
$t(x)$
, we cannot just set
![]() $t(f^n(x))=\sigma ^n (t(x))$
to satisfy property (3) because this would change
$t(f^n(x))=\sigma ^n (t(x))$
to satisfy property (3) because this would change
![]() $\kappa $
in the definition of the telescope, so we might lose property (1). Notice that correcting (flipping)
$\kappa $
in the definition of the telescope, so we might lose property (1). Notice that correcting (flipping)
![]() $\tilde t(x)$
to
$\tilde t(x)$
to
![]() $t(x)$
does not change
$t(x)$
does not change
![]() $C(\nu )$
The same goes for flipping any
$C(\nu )$
The same goes for flipping any
![]() $t(y)$
in the grand orbit of x. But the flipping can make
$t(y)$
in the grand orbit of x. But the flipping can make
![]() $f^\ell (R_{t(y)})=R_{t(f^N(x)}$
for
$f^\ell (R_{t(y)})=R_{t(f^N(x)}$
for
![]() $f^\ell (y)=f^N(x)$
where
$f^\ell (y)=f^N(x)$
where
![]() $N=n_{k_m}$
with
$N=n_{k_m}$
with
![]() $G(R_{t(f^\ell (y))})\cap \partial B(f^\ell (y),r/2)>L_{r/2}$
, thus yielding (3).
$G(R_{t(f^\ell (y))})\cap \partial B(f^\ell (y),r/2)>L_{r/2}$
, thus yielding (3).
4. Lemmas
Recall that for any
![]() $z\in J^{\prime }_\infty $
we define
$z\in J^{\prime }_\infty $
we define
![]() $z_m=f^m(z)$
for any
$z_m=f^m(z)$
for any
![]() $m\in \mathbb {Z}$
. This makes sense since f is invertible on
$m\in \mathbb {Z}$
. This makes sense since f is invertible on
![]() $J^{\prime }_\infty $
; see (E).
$J^{\prime }_\infty $
; see (E).
Lemma 4.1. Let
![]() $z(k)\in \bigcup _{j=0}^{p_{n_k}-1}f^{j}(J_{n_k})$
, where
$z(k)\in \bigcup _{j=0}^{p_{n_k}-1}f^{j}(J_{n_k})$
, where
![]() $n_k\nearrow \infty $
.
$n_k\nearrow \infty $
.
-
(a) If
 $z(k)\to z$
then
$z(k)\to z$
then
 $z\in J_\infty $
.
$z\in J_\infty $
. -
(b)
 $z\in J_{n,x}\cap J^{\prime }_\infty $
yields
$z\in J_{n,x}\cap J^{\prime }_\infty $
yields
 $z_{\pm p_n}\in J_{n,x}$
. If, in addition to (a),
$z_{\pm p_n}\in J_{n,x}$
. If, in addition to (a),
 $z(k)\in J^{\prime }_\infty $
for all k and
$z(k)\in J^{\prime }_\infty $
for all k and
 $w(k)\to w$
where
$w(k)\to w$
where
 $w(k)=z(k)_{e p_{n_k}}$
, where e is always either
$w(k)=z(k)_{e p_{n_k}}$
, where e is always either
 $1$
or
$1$
or
 $-1$
, then z and w are in the same component of
$-1$
, then z and w are in the same component of
 $J_\infty $
.
$J_\infty $
. -
(c) If
 $z(k)\in E_\epsilon $
for all k and
$z(k)\in E_\epsilon $
for all k and
 $t(z(k))\to t$
(where
$t(z(k))\to t$
(where
 $E_\epsilon $
,
$E_\epsilon $
,
 $t(z(k))$
are defined in Proposition 3.1), then the ray
$t(z(k))$
are defined in Proposition 3.1), then the ray
 $R_t$
lands at the limit point z. In particular, given
$R_t$
lands at the limit point z. In particular, given
 $\sigma>0$
, there is
$\sigma>0$
, there is
 $\Delta (\sigma )>0$
such that
$\Delta (\sigma )>0$
such that
 $|x_1-x_2|<\sigma $
for some
$|x_1-x_2|<\sigma $
for some
 $x_1,x_2\in E_\epsilon $
whenever
$x_1,x_2\in E_\epsilon $
whenever
 $|t(x_1)-t(x_2)|<\Delta (\sigma )$
.
$|t(x_1)-t(x_2)|<\Delta (\sigma )$
.
Proof. (a) Assume the contrary. Then there is n such that
![]() $d:=d(z, \bigcup _{j=0}^{p_{n}-1}{f^j(J_{n}))>0}$
. As, for any
$d:=d(z, \bigcup _{j=0}^{p_{n}-1}{f^j(J_{n}))>0}$
. As, for any
![]() $n_k\ge n$
,
$n_k\ge n$
,
![]() $z(k)\in \bigcup _{j=0}^{p_{n_k}-1}f^j(J_{n_k})$
, where the latter union is a subset of
$z(k)\in \bigcup _{j=0}^{p_{n_k}-1}f^j(J_{n_k})$
, where the latter union is a subset of
![]() $\bigcup _{j=0}^{p_{n}-1}f^j(J_{n})$
, the distance between z and
$\bigcup _{j=0}^{p_{n}-1}f^j(J_{n})$
, the distance between z and
![]() $z_k$
is at least d, a contradiction.
$z_k$
is at least d, a contradiction.
(b)
![]() $z_{\pm p_n}\in J_{n,x}$
by combinatorics and definitions of points
$z_{\pm p_n}\in J_{n,x}$
by combinatorics and definitions of points
![]() $z_{m}$
. In particular, for every k,
$z_{m}$
. In particular, for every k,
![]() $z(k)$
and
$z(k)$
and
![]() $w(k)$
are in the same component
$w(k)$
are in the same component
![]() $f^{j_k}(J_{n_k})$
of
$f^{j_k}(J_{n_k})$
of
![]() $\bigcup _{j=0}^{p_{n_k}-1}f^{j}(J_{n_k})$
. By (a), any limit set A of the sequence of compacts
$\bigcup _{j=0}^{p_{n_k}-1}f^{j}(J_{n_k})$
. By (a), any limit set A of the sequence of compacts
![]() $(f^{j_k}(J_{n_k}))$
in the Hausdorff metric is a subset of
$(f^{j_k}(J_{n_k}))$
in the Hausdorff metric is a subset of
![]() $J_\infty $
. On the other hand, A is connected as each set
$J_\infty $
. On the other hand, A is connected as each set
![]() $f^{j_k}(J_{n_k})$
is connected. This proves (b).
$f^{j_k}(J_{n_k})$
is connected. This proves (b).
(c) We prove only the first claim as the second one directly follows from it. Fix any
![]() $\nu \in (0,r)$
and choose
$\nu \in (0,r)$
and choose
![]() $k_0$
such that for any
$k_0$
such that for any
![]() $k>k_0$
,
$k>k_0$
,
![]() $B(z(k), \nu )\subset B(z,11/10\nu )$
. Then, by Proposition 3.1, part (1), for each
$B(z(k), \nu )\subset B(z,11/10\nu )$
. Then, by Proposition 3.1, part (1), for each
![]() $k>k_0$
, the first intersection of the ray
$k>k_0$
, the first intersection of the ray
![]() $R_{t(z_k)}$
with the boundary of
$R_{t(z_k)}$
with the boundary of
![]() $B(z,(11/10) \nu )$
has level at least
$B(z,(11/10) \nu )$
has level at least
![]() $C(\nu )$
. It follows, for any
$C(\nu )$
. It follows, for any
![]() $0<C<C(\nu )$
, that the sequence of arcs of the rays
$0<C<C(\nu )$
, that the sequence of arcs of the rays
![]() $R_{t_{z_k}}$
between the levels C and
$R_{t_{z_k}}$
between the levels C and
![]() $ C(\nu )$
does not exit
$ C(\nu )$
does not exit
![]() $B(z,(11/10) \nu )$
for all
$B(z,(11/10) \nu )$
for all
![]() $k>k_0$
. As
$k>k_0$
. As
![]() $\nu>0$
and
$\nu>0$
and
![]() $C\in (0, \tilde C(\nu ))$
can be chosen arbitrary small,
$C\in (0, \tilde C(\nu ))$
can be chosen arbitrary small,
![]() $R_t$
must land at z.
$R_t$
must land at z.
By Lemma 4.1(c), if the arguments
![]() $t(x),t(x')$
of
$t(x),t(x')$
of
![]() $x,x'\in E_\epsilon $
are close then
$x,x'\in E_\epsilon $
are close then
![]() $x,x'$
are close as well.
$x,x'$
are close as well.
Definition 4.2. Given
![]() $\epsilon $
and
$\epsilon $
and
![]() $\rho $
, we define
$\rho $
, we define
![]() $\delta $
as follows. First, for
$\delta $
as follows. First, for
![]() $\hat r\in (0,1)$
and
$\hat r\in (0,1)$
and
![]() $\hat C>0$
, we define
$\hat C>0$
, we define
![]() $\hat \delta =\hat \delta (\hat r,\hat C)>0$
. Namely, let
$\hat \delta =\hat \delta (\hat r,\hat C)>0$
. Namely, let
![]() $C_0>0$
be so that the distance between the equipotential of level
$C_0>0$
be so that the distance between the equipotential of level
![]() $C_0$
and
$C_0$
and
![]() $J(f)$
is bigger than
$J(f)$
is bigger than
![]() $1$
. Then
$1$
. Then
![]() $\hat \delta =\hat \delta (\hat r/2,\hat C)>0$
is such that for any
$\hat \delta =\hat \delta (\hat r/2,\hat C)>0$
is such that for any
![]() $C\in [\hat C, C_0]$
, if
$C\in [\hat C, C_0]$
, if
![]() $w_1,w_2$
lie on the same equipotential
$w_1,w_2$
lie on the same equipotential
![]() $\Gamma $
of level C and the difference between external arguments of
$\Gamma $
of level C and the difference between external arguments of
![]() $w_1,w_2$
is less than
$w_1,w_2$
is less than
![]() $\hat \delta $
, then the length of the shortest arc of the equipotential
$\hat \delta $
, then the length of the shortest arc of the equipotential
![]() $\Gamma $
between
$\Gamma $
between
![]() $w_1$
and
$w_1$
and
![]() $w_2$
is less than
$w_2$
is less than
![]() $\hat r/2$
. Apply Lemma 4.1(c) with
$\hat r/2$
. Apply Lemma 4.1(c) with
![]() $\sigma =\rho /4$
and find the corresponding
$\sigma =\rho /4$
and find the corresponding
![]() $\Delta (\rho /4)$
. Let
$\Delta (\rho /4)$
. Let
 $$ \begin{align*}\delta=\delta(\epsilon, \rho):=\min\bigg\{\hat\delta(\rho, C(\rho/2)), \Delta\bigg(\frac{\rho}{4}\bigg)\bigg\},\end{align*} $$
$$ \begin{align*}\delta=\delta(\epsilon, \rho):=\min\bigg\{\hat\delta(\rho, C(\rho/2)), \Delta\bigg(\frac{\rho}{4}\bigg)\bigg\},\end{align*} $$
where
![]() $C(\nu )$
is defined in Proposition 3.1.
$C(\nu )$
is defined in Proposition 3.1.
In the next two lemmas we construct curves with special properties. The idea is as follows. Let
![]() $x\in E_\epsilon \cap J_{n,x}$
. Then
$x\in E_\epsilon \cap J_{n,x}$
. Then
![]() $x_{-p_n}\in J_{n,x}$
. It is easy to get a curve
$x_{-p_n}\in J_{n,x}$
. It is easy to get a curve
![]() $\gamma $
in
$\gamma $
in
![]() $A(\infty )$
. Begin with an arc from a point
$A(\infty )$
. Begin with an arc from a point
![]() $b\in R_{t(x)}$
to
$b\in R_{t(x)}$
to
![]() $g_{p_n}(b)$
and then iterate this arc by
$g_{p_n}(b)$
and then iterate this arc by
![]() $g_{p_n}$
. In this way we get a curve
$g_{p_n}$
. In this way we get a curve
![]() $\gamma $
such that
$\gamma $
such that
![]() $g^{p_n}(\gamma )\subset \gamma $
, hence
$g^{p_n}(\gamma )\subset \gamma $
, hence
![]() $\gamma $
lands at a fixed point a of
$\gamma $
lands at a fixed point a of
![]() $f^{p_n}$
. We show in the next lemma (in a more general setting) that if both points
$f^{p_n}$
. We show in the next lemma (in a more general setting) that if both points
![]() $x,x_{-p_n}$
are either in the range of the covering (2.2) (condition (I)) or in the range of the covering (2.3) (condition (II)) then
$x,x_{-p_n}$
are either in the range of the covering (2.2) (condition (I)) or in the range of the covering (2.3) (condition (II)) then
![]() $a\in J_{n,x}$
. This implies that a has to be the
$a\in J_{n,x}$
. This implies that a has to be the
![]() $\beta $
-fixed point of
$\beta $
-fixed point of
![]() $f^{p_n}: J_{n,x}\to J_{n,x}$
. In Lemma 4.5, assuming additionally that
$f^{p_n}: J_{n,x}\to J_{n,x}$
. In Lemma 4.5, assuming additionally that
![]() $f^{p_n}$
is satellite, we ‘rotate’ the curve
$f^{p_n}$
is satellite, we ‘rotate’ the curve
![]() $\gamma $
by
$\gamma $
by
![]() $g_{p_{n-1}}$
to put the set
$g_{p_{n-1}}$
to put the set
![]() $J_{n,x}$
in a ‘sector’ bounded by
$J_{n,x}$
in a ‘sector’ bounded by
![]() $\gamma $
and by its ‘rotation’. In Lemmas 4.7–4.8 we consider the case of doubling for which condition (II) usually does not hold.
$\gamma $
and by its ‘rotation’. In Lemmas 4.7–4.8 we consider the case of doubling for which condition (II) usually does not hold.
In what follows, we use the following notation: given
![]() $p,q\in \mathbb {N}$
, let
$p,q\in \mathbb {N}$
, let
 $$ \begin{align*}E_{\epsilon,p,q}=\bigcap_{j=0}^{q-1} f^{jp}(E_\epsilon).\end{align*} $$
$$ \begin{align*}E_{\epsilon,p,q}=\bigcap_{j=0}^{q-1} f^{jp}(E_\epsilon).\end{align*} $$
This is a closed subset of
![]() $E_\epsilon $
of points x such that
$E_\epsilon $
of points x such that
![]() $x_{-jp}\in E_\epsilon $
for
$x_{-jp}\in E_\epsilon $
for
![]() $j=0,1,\ldots ,q-1$
. As
$j=0,1,\ldots ,q-1$
. As
![]() $f: J^{\prime }_\infty \to J^{\prime }_\infty $
is a
$f: J^{\prime }_\infty \to J^{\prime }_\infty $
is a
![]() $\mu $
-automorphism,
$\mu $
-automorphism,
![]() $\mu (E_{\epsilon ,p,q})>1-q\epsilon $
. Notice that this bound is independent of p.
$\mu (E_{\epsilon ,p,q})>1-q\epsilon $
. Notice that this bound is independent of p.
For every
![]() $n>0$
consider the closed set
$n>0$
consider the closed set
![]() $E_{\epsilon , p_n, q}$
. Let
$E_{\epsilon , p_n, q}$
. Let
![]() $x\in E_{\epsilon , p_n, q}$
. Denote for brevity
$x\in E_{\epsilon , p_n, q}$
. Denote for brevity
By Lemma 4.1(b),
![]() $x^k\in J_{n,x}$
. Hence,
$x^k\in J_{n,x}$
. Hence,
![]() $t(x^k)\in s_{n, j_n(x)}\subset S_{n,j_n(x)}$
,
$t(x^k)\in s_{n, j_n(x)}\subset S_{n,j_n(x)}$
,
![]() $0\le k\le q-1$
.
$0\le k\le q-1$
.
Recall that for a semi-open curve
![]() $l: [0,1)\to \mathbb {C}$
, we say that l lands at, or tends to, or converges to a point
$l: [0,1)\to \mathbb {C}$
, we say that l lands at, or tends to, or converges to a point
![]() $z\in \mathbb {C}$
if there exists
$z\in \mathbb {C}$
if there exists
![]() $\lim _{t\to 1}l(t)=z$
. Then
$\lim _{t\to 1}l(t)=z$
. Then
![]() $l(0)$
, z are endpoints of the curve and
$l(0)$
, z are endpoints of the curve and
![]() $l(0)$
is called also the starting point of l.
$l(0)$
is called also the starting point of l.
Lemma 4.3. Fix
![]() $\epsilon>0$
and consider the set
$\epsilon>0$
and consider the set
![]() $E_\epsilon $
with the corresponding constant
$E_\epsilon $
with the corresponding constant
![]() $r(\epsilon )>0$
. Fix
$r(\epsilon )>0$
. Fix
![]() $\rho \in (0,r(\epsilon )/3)$
. Let
$\rho \in (0,r(\epsilon )/3)$
. Let
![]() $\delta :=\delta (\epsilon , \rho )$
from Definition 4.2. For every
$\delta :=\delta (\epsilon , \rho )$
from Definition 4.2. For every
![]() $q\ge 2$
there exist
$q\ge 2$
there exist
![]() $\tilde n$
,
$\tilde n$
,
![]() $\tilde C$
as follows.
$\tilde C$
as follows.
For every
![]() $n>\tilde n$
consider the closed set
$n>\tilde n$
consider the closed set
![]() $E_{\epsilon , p_n, q}$
. Fix
$E_{\epsilon , p_n, q}$
. Fix
![]() $0\le i<j\le q-1$
. Assume, for an arbitrary n as above, that either (I)
$0\le i<j\le q-1$
. Assume, for an arbitrary n as above, that either (I)
![]() $t(x^j)$
and
$t(x^j)$
and
![]() $t(x^i)$
belong to a single component of
$t(x^i)$
belong to a single component of
![]() $s_{n, j_n(x)}$
, or (II) the map
$s_{n, j_n(x)}$
, or (II) the map
![]() $\sigma ^{j_n(x)-1}: S_{n,1}\to S_{n, j_n(x)}$
is a homeomorphism and the length of the arc
$\sigma ^{j_n(x)-1}: S_{n,1}\to S_{n, j_n(x)}$
is a homeomorphism and the length of the arc
![]() $S_{n, j_n(x)}$
is less than
$S_{n, j_n(x)}$
is less than
![]() $\delta $
.
$\delta $
.
Then the following statements hold.
-
(a) The map
 $f^{(j-i) p_n}: g_{(j-i) p_n}(B(x^i,\rho ))\to B(x^i,\rho )$
has a unique fixed point
$f^{(j-i) p_n}: g_{(j-i) p_n}(B(x^i,\rho ))\to B(x^i,\rho )$
has a unique fixed point
 $a=a_n$
and
$a=a_n$
and
 $a\in J_{n,x}$
.
$a\in J_{n,x}$
. -
(b) There is a semi-open simple curve
such that: $$ \begin{align*}\gamma_{p_n,q,i,j}(x)\subset B(x^i, \rho)\cap A(\infty)\end{align*} $$
$$ \begin{align*}\gamma_{p_n,q,i,j}(x)\subset B(x^i, \rho)\cap A(\infty)\end{align*} $$
-
(1) it lands at a and
 $g_{(j-i) p_n}(\gamma _{p_n,q,i,j}(x))\subset \gamma _{p_n,q,i,j}(x)$
. Another end point b of
$g_{(j-i) p_n}(\gamma _{p_n,q,i,j}(x))\subset \gamma _{p_n,q,i,j}(x)$
. Another end point b of
 $\gamma _{p_n,q,i,j}(x)$
lies in
$\gamma _{p_n,q,i,j}(x)$
lies in
 $R^i$
and
$R^i$
and
 $G(b)>\tilde C/2$
,
$G(b)>\tilde C/2$
, -
(2)
 $\gamma _{p_n,q,i,j}(x)=\bigcup _{l\ge 0} g_{(j-i)p_n}^l(L_0\cup L_1)$
where the ‘fundamental arc’
$\gamma _{p_n,q,i,j}(x)=\bigcup _{l\ge 0} g_{(j-i)p_n}^l(L_0\cup L_1)$
where the ‘fundamental arc’
 $L_0\cup L_1$
consists of an arc
$L_0\cup L_1$
consists of an arc
 $L_0$
of an equipotential of the level at least
$L_0$
of an equipotential of the level at least
 $\tilde C/2$
that joins a point
$\tilde C/2$
that joins a point
 $b\in R^i$
with a point
$b\in R^i$
with a point
 $b_1\in R^j$
, being extended by an arc
$b_1\in R^j$
, being extended by an arc
 $L_1$
of the ray
$L_1$
of the ray
 $R^j$
between points
$R^j$
between points
 $b_1$
and
$b_1$
and
 $g_{(j-i)p_n}(b)\in R^j$
; in particular, the Green function
$g_{(j-i)p_n}(b)\in R^j$
; in particular, the Green function
 $G(y)$
at a point y is not increasing as y moves from b to a along
$G(y)$
at a point y is not increasing as y moves from b to a along
 $\gamma _{p_n,q,i,j}(x)$
,
$\gamma _{p_n,q,i,j}(x)$
, -
(3) the point a is the landing point of a ray
 $R(a)$
which is fixed by
$R(a)$
which is fixed by
 $f^{(j-i) p_n}$
and which is homotopic to
$f^{(j-i) p_n}$
and which is homotopic to
 $\gamma _{p_n,q,i,j}(x)$
through a family of curves in
$\gamma _{p_n,q,i,j}(x)$
through a family of curves in
 $A(\infty )$
with the fixed end point a.
$A(\infty )$
with the fixed end point a. -
(4) the arguments of all points of the curve
 $g_{(j-i) p_n}(\gamma _{p_n,q,i,j}(x))$
lie in a single component of
$g_{(j-i) p_n}(\gamma _{p_n,q,i,j}(x))$
lie in a single component of
 $s^1_{n, j_n(x)}$
in case (I) and in a single component of
$s^1_{n, j_n(x)}$
in case (I) and in a single component of
 $s_{n,j_n(x)}$
in case (II) (recall that
$s_{n,j_n(x)}$
in case (II) (recall that
 $s^1_{n, j_n(x)}$
has four components and
$s^1_{n, j_n(x)}$
has four components and
 $s_{n,j_n(x)}$
has two components, see §2, (C)).
$s_{n,j_n(x)}$
has two components, see §2, (C)).
Besides,
(4.1)as $$ \begin{align} |a-x^j|\to 0 \quad\text{and}\quad \log\frac{|(g_{(j-i)p_n})'(x^j)|}{|(g_{(j-i)p_n})'(a)|}\to 0 \end{align} $$
$$ \begin{align} |a-x^j|\to 0 \quad\text{and}\quad \log\frac{|(g_{(j-i)p_n})'(x^j)|}{|(g_{(j-i)p_n})'(a)|}\to 0 \end{align} $$
 $n\to \infty $
, uniformly in
$n\to \infty $
, uniformly in
 $x^j$
and q.
$x^j$
and q.
-
-
(c) If
 $j-i=1$
then
$j-i=1$
then
 $a=\beta _{n,j_n(x)}$
where
$a=\beta _{n,j_n(x)}$
where
 $\beta _{n,j_n(x)}=f^{j_n(x)-1}(\beta _n)$
, the non-separating fixed point of
$\beta _{n,j_n(x)}=f^{j_n(x)-1}(\beta _n)$
, the non-separating fixed point of
 $f^{p_n}:J_{n,x}\to J_{n,x}$
. Moreover, as
$f^{p_n}:J_{n,x}\to J_{n,x}$
. Moreover, as $$ \begin{align*}\chi(\beta_{n,j_n(x)}):=\frac{1}{p_n}\log |(f^{p_n})'(\beta_{n,j_n(x)})|=\frac{1}{p_n}\log |(f^{p_n})'(\beta_{n})|\to \chi(\mu)\end{align*} $$
$$ \begin{align*}\chi(\beta_{n,j_n(x)}):=\frac{1}{p_n}\log |(f^{p_n})'(\beta_{n,j_n(x)})|=\frac{1}{p_n}\log |(f^{p_n})'(\beta_{n})|\to \chi(\mu)\end{align*} $$
 $n\to \infty $
.
$n\to \infty $
.
Remark 4.4. Note that
![]() $a\notin J_\infty $
while
$a\notin J_\infty $
while
![]() $x, x^1,\ldots ,x^{q-1}\in J_\infty $
.
$x, x^1,\ldots ,x^{q-1}\in J_\infty $
.
Proof. Fix
![]() $n_0$
such that, for every
$n_0$
such that, for every
![]() $n>n_0$
and
$n>n_0$
and
![]() $x\in E_\epsilon $
, the length of each ‘window’ of
$x\in E_\epsilon $
, the length of each ‘window’ of
![]() $s_{n, j_n(x)}$
is less than
$s_{n, j_n(x)}$
is less than
![]() $\delta $
. Therefore, for
$\delta $
. Therefore, for
![]() $n>n_0$
, in either case (I), (II),
$n>n_0$
, in either case (I), (II),
which implies, in particular, that
![]() $|x^i-x^j|<\rho /4$
.
$|x^i-x^j|<\rho /4$
.
Denote
![]() $G_n:=g_{(j-i)p_n}$
, which is a holomorphic univalent function in
$G_n:=g_{(j-i)p_n}$
, which is a holomorphic univalent function in
![]() $B(x^i,\rho )$
. Since
$B(x^i,\rho )$
. Since
![]() $g_m$
are uniform contractions there is
$g_m$
are uniform contractions there is
![]() $n_1$
such that
$n_1$
such that
![]() $G_n(\overline {B(x^i,\rho )})\subset B(x^i,\rho /2)$
whenever
$G_n(\overline {B(x^i,\rho )})\subset B(x^i,\rho /2)$
whenever
![]() $n>n_1$
. Let
$n>n_1$
. Let
![]() $\tilde n=\max \{n_0, n_1\}$
.
$\tilde n=\max \{n_0, n_1\}$
.
Let also
![]() $\tilde C=C(\rho /2)$
, where
$\tilde C=C(\rho /2)$
, where
![]() $C(\nu )$
is defined in Proposition 3.1.
$C(\nu )$
is defined in Proposition 3.1.
Let
![]() $a=a_n$
be the unique fixed point of the latter map
$a=a_n$
be the unique fixed point of the latter map
![]() $G_n$
. We construct the curve
$G_n$
. We construct the curve
![]() $\gamma _{p_n,q,i,j}(x)$
to the point a as follows. Firstly, joint a point
$\gamma _{p_n,q,i,j}(x)$
to the point a as follows. Firstly, joint a point
![]() $b\in R^i$
,
$b\in R^i$
,
![]() $G(b)=(3/4)\tilde C$
, to a point
$G(b)=(3/4)\tilde C$
, to a point
![]() $b_1\in R^j$
by an arc
$b_1\in R^j$
by an arc
![]() $L_0$
of the equipotential
$L_0$
of the equipotential
![]() $\{G(z)=(3/4)\tilde C\}$
. By the choice of
$\{G(z)=(3/4)\tilde C\}$
. By the choice of
![]() $\delta>0$
,
$\delta>0$
,
![]() $L_0{\kern-1pt}\subset{\kern-1pt} B(x^i,\rho )$
. Secondly, connect
$L_0{\kern-1pt}\subset{\kern-1pt} B(x^i,\rho )$
. Secondly, connect
![]() $b_1$
to the point
$b_1$
to the point
![]() $g_{(j-i)p_n}(b){\kern-1pt}\in{\kern-1pt} R^j$
by an arc
$g_{(j-i)p_n}(b){\kern-1pt}\in{\kern-1pt} R^j$
by an arc
![]() $L_1{\kern-1pt}\subset{\kern-1pt} R^j$
. Now let
$L_1{\kern-1pt}\subset{\kern-1pt} R^j$
. Now let
![]() $\gamma _{p_n,q,i,j}(x)=\bigcup _{l\ge 0} g_{(j-i)p_n}^l(L_0\cup L_1)$
. Then properties (1), (2) in (b) are immediate and (3) follows from general properties of conformal maps. Now, by Proposition 3.1(2) and (4.2), for all n big enough,
$\gamma _{p_n,q,i,j}(x)=\bigcup _{l\ge 0} g_{(j-i)p_n}^l(L_0\cup L_1)$
. Then properties (1), (2) in (b) are immediate and (3) follows from general properties of conformal maps. Now, by Proposition 3.1(2) and (4.2), for all n big enough,
![]() $x^j=g_{(j-i)p_n}(x^i)\in g_{(j-i)p_n}(B(x^i,\rho ))\subset B(x^i,\rho )$
; moreover, the modulus of the annulus
$x^j=g_{(j-i)p_n}(x^i)\in g_{(j-i)p_n}(B(x^i,\rho ))\subset B(x^i,\rho )$
; moreover, the modulus of the annulus
![]() $B(x^i,\rho )\setminus g_{(j-i)p_n}(B(x^i,\rho ))$
tends to
$B(x^i,\rho )\setminus g_{(j-i)p_n}(B(x^i,\rho ))$
tends to
![]() $\infty $
as
$\infty $
as
![]() $n\to \infty $
. Therefore, (4.1) follows from Koebe, see e.g. [Reference Carleson and Gamelin2, Section 1.1], and Proposition 3.1(2).
$n\to \infty $
. Therefore, (4.1) follows from Koebe, see e.g. [Reference Carleson and Gamelin2, Section 1.1], and Proposition 3.1(2).
It remains to show property (3) and that
![]() $a\in J_{n,x}$
. Consider case (II), which is equivalent to saying that the map
$a\in J_{n,x}$
. Consider case (II), which is equivalent to saying that the map
![]() $\sigma ^{p_n}: s\to S_{n, j_n(x)}$
is a homeomorphism on each of two components s of
$\sigma ^{p_n}: s\to S_{n, j_n(x)}$
is a homeomorphism on each of two components s of
![]() $s_{n, j_n(x)}$
. Let
$s_{n, j_n(x)}$
. Let
![]() $\Lambda $
be the set of arguments of points of the curve
$\Lambda $
be the set of arguments of points of the curve
![]() $\Gamma :=g_{(j-i) p_n}(\gamma _{p_n,q,i,j}(x))$
. Let s be a component that contains
$\Gamma :=g_{(j-i) p_n}(\gamma _{p_n,q,i,j}(x))$
. Let s be a component that contains
![]() $t(x^j)$
. Assume, by contradiction, that
$t(x^j)$
. Assume, by contradiction, that
![]() $\Lambda $
contains t which is in the boundary of s. Then t is the argument of a point of
$\Lambda $
contains t which is in the boundary of s. Then t is the argument of a point of
![]() $G_n^l(L_0)$
, for some
$G_n^l(L_0)$
, for some
![]() $l\ge 1$
, and hence
$l\ge 1$
, and hence
![]() $\sigma ^{l(j-i)p_n}(t)$
is simultaneously the argument of a point of
$\sigma ^{l(j-i)p_n}(t)$
is simultaneously the argument of a point of
![]() $L_0$
and in the boundary of
$L_0$
and in the boundary of
![]() $S_{n,j_n(x)}$
, a contradiction. Case (I) is similar. Property (3) is verified. In fact, we have proved more: for
$S_{n,j_n(x)}$
, a contradiction. Case (I) is similar. Property (3) is verified. In fact, we have proved more: for
![]() $k=0,1,\ldots ,j-i-1$
, the set
$k=0,1,\ldots ,j-i-1$
, the set
![]() $\sigma ^{k p_n}(\Lambda )$
is a subset of a single (depending on k) component of
$\sigma ^{k p_n}(\Lambda )$
is a subset of a single (depending on k) component of
![]() $s_{n, j_n(x)}$
in case (II) and a single component of
$s_{n, j_n(x)}$
in case (II) and a single component of
![]() $s^1_{n, j_n(x)}$
in case (I). This implies that all points
$s^1_{n, j_n(x)}$
in case (I). This implies that all points
![]() $f^{k p_n}(a)$
,
$f^{k p_n}(a)$
,
![]() $0\le k\le j-i-1$
, of the cycle of
$0\le k\le j-i-1$
, of the cycle of
![]() $f^{p_n}$
containing a belong to the closure of
$f^{p_n}$
containing a belong to the closure of
![]() $U_{n,j_n(x)}$
in the case (II) and to the closure of
$U_{n,j_n(x)}$
in the case (II) and to the closure of
![]() $U_{n, j_n(x)-p_n}$
in the case (I). Therefore, this cycle lies in
$U_{n, j_n(x)-p_n}$
in the case (I). Therefore, this cycle lies in
![]() $J_{n,x}$
, in particular,
$J_{n,x}$
, in particular,
![]() $a\in J_{n,x}$
.
$a\in J_{n,x}$
.
Proof of (c). If
![]() $j-i=1$
then a is a fixed point of
$j-i=1$
then a is a fixed point of
![]() $f^{p_n}:J_{n,x}\to J_{n,x}$
and, moreover, the ray
$f^{p_n}:J_{n,x}\to J_{n,x}$
and, moreover, the ray
![]() $R(a)$
lands at a and is fixed by
$R(a)$
lands at a and is fixed by
![]() $f^{p_n}$
. Hence, the rotation number of a with respect to the map
$f^{p_n}$
. Hence, the rotation number of a with respect to the map
![]() $f^{p_n}:J_{n,x}\to J_{n,x}$
is zero. On the other hand,
$f^{p_n}:J_{n,x}\to J_{n,x}$
is zero. On the other hand,
![]() $\beta _{n,j_n(x)}$
is the only such a fixed point, that is,
$\beta _{n,j_n(x)}$
is the only such a fixed point, that is,
![]() $a=\beta _{n,j_n(x)}$
as claimed. Then (4.1) implies that
$a=\beta _{n,j_n(x)}$
as claimed. Then (4.1) implies that
![]() $\chi (\beta _{n,j_n(x)})\to \chi (\mu )$
.
$\chi (\beta _{n,j_n(x)})\to \chi (\mu )$
.
For the rest of the paper, let us fix Q,
![]() $\epsilon $
, r,
$\epsilon $
, r,
![]() $\rho $
,
$\rho $
,
![]() $\tilde n$
,
$\tilde n$
,
![]() $\tilde C$
and
$\tilde C$
and
![]() $\delta $
as follows:
$\delta $
as follows:
![]() $Q\in \mathbb {N}$
,
$Q\in \mathbb {N}$
,
![]() $Q>3$
, is such that
$Q>3$
, is such that
This choice is motivated by the following fact [Reference Hubbard8, Reference Levin14, Reference Pommerenke21]: if a repelling fixed point z of
![]() $f^n$
is the landing point of q rays, then
$f^n$
is the landing point of q rays, then
![]() $\chi (z):=(1/n)\log |(f^n)'(z)|\le (2/q)\log 2$
. Hence, if
$\chi (z):=(1/n)\log |(f^n)'(z)|\le (2/q)\log 2$
. Hence, if
![]() $\chi (z)>\chi (\mu )/2$
, then
$\chi (z)>\chi (\mu )/2$
, then
![]() $q<Q$
.
$q<Q$
.
Furthermore, fix
![]() $\epsilon>0$
such that
$\epsilon>0$
such that
![]() $2^{100}Q\epsilon <1$
, apply Proposition 3.1 and Lemma 4.3 and find, first,
$2^{100}Q\epsilon <1$
, apply Proposition 3.1 and Lemma 4.3 and find, first,
![]() $r=r(\epsilon )$
, then fix
$r=r(\epsilon )$
, then fix
![]() $\rho \in (0,r/32)$
and find the corresponding
$\rho \in (0,r/32)$
and find the corresponding
![]() $\tilde n$
,
$\tilde n$
,
![]() $\tilde C$
and
$\tilde C$
and
![]() $\delta $
.
$\delta $
.
Let
 $$ \begin{align*}X_n=E_{\epsilon,p_n,4}\cap E_{\epsilon, p_{n-1},Q}=\bigcap_{i=0}^3 f^{i p_n}(E_\epsilon)\bigcap_{k=0}^{Q-1} f^{k p_{n-1}}(E_\epsilon).\end{align*} $$
$$ \begin{align*}X_n=E_{\epsilon,p_n,4}\cap E_{\epsilon, p_{n-1},Q}=\bigcap_{i=0}^3 f^{i p_n}(E_\epsilon)\bigcap_{k=0}^{Q-1} f^{k p_{n-1}}(E_\epsilon).\end{align*} $$
Let us analyze several possibilities.
Lemma 4.5. There is
![]() $n_*>\tilde n$
as follows. Let
$n_*>\tilde n$
as follows. Let
![]() $n>n_*$
and
$n>n_*$
and
![]() $x\in X_n$
. Consider
$x\in X_n$
. Consider
![]() $J_{n,x}=f^{j_n(x)}(J_n)\subset f^{j_{n-1}(x)}(J_{n-1})$
so that
$J_{n,x}=f^{j_n(x)}(J_n)\subset f^{j_{n-1}(x)}(J_{n-1})$
so that
![]() $x\in J_{n,x}$
.
$x\in J_{n,x}$
.
Let
![]() $x^0=x$
and
$x^0=x$
and
![]() $x^1=x_{-p_n}$
. Assume that either (I)
$x^1=x_{-p_n}$
. Assume that either (I)
![]() $t(x^0)$
,
$t(x^0)$
,
![]() $t(x^1)$
belong to a single component of
$t(x^1)$
belong to a single component of
![]() $s_{n, j_n(x)}$
, or (II) the map
$s_{n, j_n(x)}$
, or (II) the map
![]() $\sigma ^{j_n(x)-1}: S_{n,1}\to S_{n, j_n(x)}$
is a homeomorphism and the length of the arc
$\sigma ^{j_n(x)-1}: S_{n,1}\to S_{n, j_n(x)}$
is a homeomorphism and the length of the arc
![]() $S_{n, j_n(x)}$
is less than
$S_{n, j_n(x)}$
is less than
![]() $\delta $
.
$\delta $
.
Then the following statements hold.
-
(i)
 $\chi (\beta _{n,j_n(x)})=\chi (\beta _n)\to \chi (\mu )$
as
$\chi (\beta _{n,j_n(x)})=\chi (\beta _n)\to \chi (\mu )$
as
 $n\to \infty $
and
$n\to \infty $
and
 $\chi (\beta _n)>\chi (\mu )/2$
for
$\chi (\beta _n)>\chi (\mu )/2$
for
 $n>n_*$
.
$n>n_*$
. -
(ii) Assume that
 $f^{p_n}$
is satellite, that is (by Lemma 2.1).
$f^{p_n}$
is satellite, that is (by Lemma 2.1).
 $\beta _n$
has period
$\beta _n$
has period
 $p_{n-1}$
,
$p_{n-1}$
,
 $q_n\ge 2$
with rotation number
$q_n\ge 2$
with rotation number
 $r_n/q_n$
of
$r_n/q_n$
of
 $\beta _n$
, and
$\beta _n$
, and
 $\beta _{n,j_n(x)}$
is the
$\beta _{n,j_n(x)}$
is the
 $\alpha $
(that is, separating) fixed point of
$\alpha $
(that is, separating) fixed point of
 $f^{p_{n-1}}: J_{n-1,x}\to J_{n-1,x}$
. Then
$f^{p_{n-1}}: J_{n-1,x}\to J_{n-1,x}$
. Then
 $q_n<Q$
and (4.3)
$q_n<Q$
and (4.3) $$ \begin{align} |\beta_{n,j_n(x)}-x_{-k p_{n-1}}\hspace{-1pt}|\to 0, \ n\to\infty, \text{ uniformly in } x\in X_n, \ 1\le k\le q_{n}. \end{align} $$
$$ \begin{align} |\beta_{n,j_n(x)}-x_{-k p_{n-1}}\hspace{-1pt}|\to 0, \ n\to\infty, \text{ uniformly in } x\in X_n, \ 1\le k\le q_{n}. \end{align} $$
There exist two simple semi-open curves
![]() $\gamma (x)$
and
$\gamma (x)$
and
![]() $\tilde \gamma (x)$
that satisfy the following properties.
$\tilde \gamma (x)$
that satisfy the following properties.
-
(1)
 $\gamma (x)$
and
$\gamma (x)$
and
 $\tilde \gamma (x)$
tend to
$\tilde \gamma (x)$
tend to
 $\beta _{n,j_n(x)}$
and
$\beta _{n,j_n(x)}$
and
 $\gamma (x), \tilde \gamma (x)\subset B(x^0, \rho )\cap A(\infty )$
.
$\gamma (x), \tilde \gamma (x)\subset B(x^0, \rho )\cap A(\infty )$
. -
(2)
 $\gamma (x), \tilde \gamma (x)$
consist of arcs of equipotentials and external rays. The starting point
$\gamma (x), \tilde \gamma (x)$
consist of arcs of equipotentials and external rays. The starting point
 $b_1=b_1(x)$
of
$b_1=b_1(x)$
of
 $\gamma (x)$
lies in an arc of
$\gamma (x)$
lies in an arc of
 $R_{t(x^1)}$
and the starting point
$R_{t(x^1)}$
and the starting point
 $\tilde b_1=\tilde b_1(x)$
of
$\tilde b_1=\tilde b_1(x)$
of
 $\tilde \gamma (x)$
lies in an arc of
$\tilde \gamma (x)$
lies in an arc of
 $R_{t(\tilde x)}$
where
$R_{t(\tilde x)}$
where
 $\tilde x=x_{-i p_{n-1}}$
for some
$\tilde x=x_{-i p_{n-1}}$
for some
 $i=i(x)\in \{1,\ldots , q_n-1\}$
, such that levels of
$i=i(x)\in \{1,\ldots , q_n-1\}$
, such that levels of
 $b_1$
and
$b_1$
and
 $\tilde b_1$
are equal and at least
$\tilde b_1$
are equal and at least
 $\tilde C/4$
.
$\tilde C/4$
. -
(3) One of the two curves (say,
 $\gamma (x)$
) is homotopic, through curves in
$\gamma (x)$
) is homotopic, through curves in
 $A(\infty )$
tending to
$A(\infty )$
tending to
 $\beta _{n,j_n(x)}$
, to the ray
$\beta _{n,j_n(x)}$
, to the ray
 $R_{t_{n,j_n(x)}}=f^{j_n(x)-1}(R_{t_n})$
, and the other one to the ray
$R_{t_{n,j_n(x)}}=f^{j_n(x)-1}(R_{t_n})$
, and the other one to the ray
 $R_{\tilde t_{n,j_n(x)}}=f^{j_n(x)-1}(R_{\tilde t_n})$
.
$R_{\tilde t_{n,j_n(x)}}=f^{j_n(x)-1}(R_{\tilde t_n})$
. -
(4)
 $\gamma (x)$
,
$\gamma (x)$
,
 $\tilde \gamma (x)\subset U_{n-1, j_{n-1}(x)}$
.
$\tilde \gamma (x)\subset U_{n-1, j_{n-1}(x)}$
. -
(5)
 $\gamma (x)\subset U_{n,j_n(x)}$
,
$\gamma (x)\subset U_{n,j_n(x)}$
,
 $\tilde \gamma (x)\subset U_{n,j_n(\tilde x)}$
, in particular,
$\tilde \gamma (x)\subset U_{n,j_n(\tilde x)}$
, in particular,
 $\gamma (x),\tilde \gamma (x)$
are disjoint, being completed by their common limit point
$\gamma (x),\tilde \gamma (x)$
are disjoint, being completed by their common limit point
 $\beta _{n,j_n(x)}$
and two other arcs: an arc of the ray
$\beta _{n,j_n(x)}$
and two other arcs: an arc of the ray
 $R_{t(x^1)}$
from
$R_{t(x^1)}$
from
 $b_1\in \gamma (x)$
to
$b_1\in \gamma (x)$
to
 $\infty $
and an arc of the ray
$\infty $
and an arc of the ray
 $R_{t(\tilde x)}$
from
$R_{t(\tilde x)}$
from
 $\tilde b_1\in \tilde \gamma (x)$
to
$\tilde b_1\in \tilde \gamma (x)$
to
 $\infty $
, they split the plane into two domains such that one of them contains
$\infty $
, they split the plane into two domains such that one of them contains
 $I:=J_{n,x}\setminus \beta _{n,j_n(x)}$
and the other one contains all
$I:=J_{n,x}\setminus \beta _{n,j_n(x)}$
and the other one contains all
 $q_n-1$
other different iterates
$q_n-1$
other different iterates
 $f^{k p_{n-1}}(I)$
,
$f^{k p_{n-1}}(I)$
,
 $1\le k\le q_n-1$
. The intersection of closures of all those
$1\le k\le q_n-1$
. The intersection of closures of all those
 $q_n$
sets consists of the fixed point
$q_n$
sets consists of the fixed point
 $\beta _{n,j_n(x)}$
of
$\beta _{n,j_n(x)}$
of
 $f^{p_{n-1}}$
.
$f^{p_{n-1}}$
.
Remark 4.6. Beware that the point x that determines both curves
![]() $\gamma (x)$
,
$\gamma (x)$
,
![]() $\tilde \gamma (x)$
does not belong to either of these curves.
$\tilde \gamma (x)$
does not belong to either of these curves.
Proof. Statement (i) follows from Lemma 4.3 where we take
![]() $i=0, j=1$
. Fix
$i=0, j=1$
. Fix
![]() $n_*>\tilde n$
such that
$n_*>\tilde n$
such that
![]() $\chi (\beta _n)>\chi (\mu )/2$
for all
$\chi (\beta _n)>\chi (\mu )/2$
for all
![]() $n>n_*$
.
$n>n_*$
.
Let us prove (ii). Here we build a ‘flower’ of arcs at the fixed
![]() $\beta $
of the satellite
$\beta $
of the satellite
![]() $f^{p_n}$
, starting with an arc which is fixed by
$f^{p_n}$
, starting with an arc which is fixed by
![]() $f^{p_n}$
, and then ‘rotate’ this arc by a branch of
$f^{p_n}$
, and then ‘rotate’ this arc by a branch of
![]() $f^{-p_{n-1}}$
(for which the same
$f^{-p_{n-1}}$
(for which the same
![]() $\beta $
point is also a fixed point; see (C)). Let
$\beta $
point is also a fixed point; see (C)). Let
![]() $\gamma '(x):=\gamma _{p_n,1,0,1}(x)$
where the latter curve is defined in Lemma 4.3. Then properties (1)–(3) of the curve
$\gamma '(x):=\gamma _{p_n,1,0,1}(x)$
where the latter curve is defined in Lemma 4.3. Then properties (1)–(3) of the curve
![]() $\gamma (x)$
are also satisfied for
$\gamma (x)$
are also satisfied for
![]() $\gamma '(x)$
. In particular,
$\gamma '(x)$
. In particular,
![]() $\gamma '(x)$
is homotopic to
$\gamma '(x)$
is homotopic to
![]() $R_{t_{n,j_n(x)}}$
.
$R_{t_{n,j_n(x)}}$
.
As both
![]() $\tilde t_{n,j_n(x)}, t_{n,j_n(x)}$
are external arguments of
$\tilde t_{n,j_n(x)}, t_{n,j_n(x)}$
are external arguments of
![]() $\beta _{n,j_n(x)}$
which is a
$\beta _{n,j_n(x)}$
which is a
![]() $p_{n-1}$
-periodic point of f, there is
$p_{n-1}$
-periodic point of f, there is
![]() $i\in \{1,\ldots , q_n-1\}$
such that
$i\in \{1,\ldots , q_n-1\}$
such that
![]() $\sigma ^{i p_{n-1}}(\tilde t_{n,j_n(x)})=t_{n,j_n(x)}$
. Now we use that
$\sigma ^{i p_{n-1}}(\tilde t_{n,j_n(x)})=t_{n,j_n(x)}$
. Now we use that
![]() $x\in E_{\epsilon , p_{n-1},Q}$
and that
$x\in E_{\epsilon , p_{n-1},Q}$
and that
![]() $q_{n}<Q$
to prove (4.3). Indeed, for each
$q_{n}<Q$
to prove (4.3). Indeed, for each
![]() $k=\{1,\ldots , q_n\}$
, since
$k=\{1,\ldots , q_n\}$
, since
![]() $f{\kern-1pt}:{\kern-1pt}J_\infty '{\kern-1pt}\to{\kern-1pt} J_\infty '$
is a homeomorphism and
$f{\kern-1pt}:{\kern-1pt}J_\infty '{\kern-1pt}\to{\kern-1pt} J_\infty '$
is a homeomorphism and
![]() $x_{-k p_{n-1}}{\kern-1pt}\in{\kern-1pt} E_\epsilon $
, we have
$x_{-k p_{n-1}}{\kern-1pt}\in{\kern-1pt} E_\epsilon $
, we have
![]() $g_{p_n}{\kern-1pt}={\kern-1pt}g_{(q_{n}-k) p_{n-1}}\circ g_{k p_{n-1}}$
. Hence, if
$g_{p_n}{\kern-1pt}={\kern-1pt}g_{(q_{n}-k) p_{n-1}}\circ g_{k p_{n-1}}$
. Hence, if
![]() $\beta '=g_{k p_{n-1}}(\beta _{n,j_n(x)})$
, then
$\beta '=g_{k p_{n-1}}(\beta _{n,j_n(x)})$
, then
![]() $\beta _{n,j_n(x)}=g_{(q_{n-1}-k) p_{n-1}}(\beta ')$
, implying that
$\beta _{n,j_n(x)}=g_{(q_{n-1}-k) p_{n-1}}(\beta ')$
, implying that
![]() $\beta '=f^{(q_{n}-k) p_{n-1}}(\beta _{n,j_n(x)})=\beta _{n,j_n(x)}$
. Then
$\beta '=f^{(q_{n}-k) p_{n-1}}(\beta _{n,j_n(x)})=\beta _{n,j_n(x)}$
. Then
![]() $\beta _{n,j_n(x)}, x_{-k p_{n-1}}\in g_{k p_{n-1}}(B(x,\rho ))$
which, along with Proposition 3.1, part (2), implies (4.3).
$\beta _{n,j_n(x)}, x_{-k p_{n-1}}\in g_{k p_{n-1}}(B(x,\rho ))$
which, along with Proposition 3.1, part (2), implies (4.3).
In turn, (4.3) implies that, provided n is big,
![]() $g_{k p_{n-1}}: B(y,\rho /2)\to B(y,\rho /2)$
uniformly in
$g_{k p_{n-1}}: B(y,\rho /2)\to B(y,\rho /2)$
uniformly in
![]() $k=0,1,\ldots , q_n$
where y is either
$k=0,1,\ldots , q_n$
where y is either
![]() $\beta _{n,j_n(x)}$
or
$\beta _{n,j_n(x)}$
or
![]() $x_{-k p_{n-1}}$
.
$x_{-k p_{n-1}}$
.
Now we consider a curve
![]() $g_{i \tilde p_{n}}(\gamma '(x))$
that starts at
$g_{i \tilde p_{n}}(\gamma '(x))$
that starts at
![]() $x_{-i \tilde p_{n}}$
and tends to
$x_{-i \tilde p_{n}}$
and tends to
![]() $\beta _{n,j_n(x)}$
. By Proposition 3.1 coupled with (4.3), one can join
$\beta _{n,j_n(x)}$
. By Proposition 3.1 coupled with (4.3), one can join
![]() $x_{-i p_{n-1}}$
by an arc of the ray
$x_{-i p_{n-1}}$
by an arc of the ray
![]() $R_{t(x_{-i p_{n-1}})}$
inside of
$R_{t(x_{-i p_{n-1}})}$
inside of
![]() $B(x,\rho /2)$
up to a point of level
$B(x,\rho /2)$
up to a point of level
![]() $\tilde C/4$
. This will be the required curve
$\tilde C/4$
. This will be the required curve
![]() $\tilde \gamma (x)$
. To get the curve
$\tilde \gamma (x)$
. To get the curve
![]() $\gamma (x)$
we modify
$\gamma (x)$
we modify
![]() $\gamma '(x)=\gamma _{p_n,1,0,1}(x)=\bigcup _{l\ge 0} g_{p_{n}}^l(L_0\cup L_1)$
by cutting off the arc
$\gamma '(x)=\gamma _{p_n,1,0,1}(x)=\bigcup _{l\ge 0} g_{p_{n}}^l(L_0\cup L_1)$
by cutting off the arc
![]() $L_0$
of an equipotential:
$L_0$
of an equipotential:
![]() $\gamma (x)=\gamma '(x)\setminus L_0$
(see Lemma 4.3 for details about
$\gamma (x)=\gamma '(x)\setminus L_0$
(see Lemma 4.3 for details about
![]() $L_0$
). Properties (1)–(5) follow.
$L_0$
). Properties (1)–(5) follow.
Given a point
![]() $x=x^0$
and n such that
$x=x^0$
and n such that
![]() $x\in f^{j}(J_n)\cap E_{\epsilon , p_n, 1}$
, where
$x\in f^{j}(J_n)\cap E_{\epsilon , p_n, 1}$
, where
![]() $j=j_n(x)$
, let
$j=j_n(x)$
, let
![]() $x^1=x_{-p_n}$
and
$x^1=x_{-p_n}$
and
![]() $t(x^0)$
,
$t(x^0)$
,
![]() $t(x^1)$
be the arguments of
$t(x^1)$
be the arguments of
![]() $x^0$
,
$x^0$
,
![]() $x^1$
as in Proposition 3.1. We call
$x^1$
as in Proposition 3.1. We call
![]() $x n$
-friendly if
$x n$
-friendly if
![]() $t(x^0)$
and
$t(x^0)$
and
![]() $t(x^{1})$
lie in the same component of
$t(x^{1})$
lie in the same component of
![]() $s_{n,j}$
and n-unfriendly otherwise (or simply friendly and unfriendly if n is clear from the context). The name reflects the fact that for an n-friendly point x condition (I) of Lemma 4.5 always holds for
$s_{n,j}$
and n-unfriendly otherwise (or simply friendly and unfriendly if n is clear from the context). The name reflects the fact that for an n-friendly point x condition (I) of Lemma 4.5 always holds for
![]() $x^1=x$
and
$x^1=x$
and
![]() $x^2=x_{-p_n}$
, so Lemma 4.5 always applies.
$x^2=x_{-p_n}$
, so Lemma 4.5 always applies.
When the rotation number of
![]() $\alpha _n$
is equal to
$\alpha _n$
is equal to
![]() $1/2$
we have the following lemma.
$1/2$
we have the following lemma.
Lemma 4.7. There is
![]() $\tilde C_3>0$
(depending only on fixed
$\tilde C_3>0$
(depending only on fixed
![]() $\epsilon $
and
$\epsilon $
and
![]() $\rho $
) as follows. Suppose that, for some
$\rho $
) as follows. Suppose that, for some
![]() $n>\tilde n$
, the rotation number of the separating fixed point
$n>\tilde n$
, the rotation number of the separating fixed point
![]() $\alpha _n$
is equal to
$\alpha _n$
is equal to
![]() $1/2$
. Let
$1/2$
. Let
![]() $z=z^0\in f^j(J_n)\cap E_{\epsilon , p_n, 3}$
and
$z=z^0\in f^j(J_n)\cap E_{\epsilon , p_n, 3}$
and
![]() $z^i=z_{-i p_n}$
,
$z^i=z_{-i p_n}$
,
![]() $i=1,2,3$
. Assume that all three points
$i=1,2,3$
. Assume that all three points
![]() $z^0, z^1, z^2$
are n-unfriendly.
$z^0, z^1, z^2$
are n-unfriendly.
Then there exist two (semi-open) curves
![]() $\gamma ^{1/2}_n(z)$
and
$\gamma ^{1/2}_n(z)$
and
![]() $\tilde \gamma ^{1/2}_n(z)$
consisting of arcs of rays and equipotentials with the following properties.
$\tilde \gamma ^{1/2}_n(z)$
consisting of arcs of rays and equipotentials with the following properties.
-
(i)
 $\gamma ^{1/2}_n(z)\subset B(z,\rho )$
,
$\gamma ^{1/2}_n(z)\subset B(z,\rho )$
,
 $\tilde \gamma ^{1/2}_n(z)\subset B(z^1,\rho )$
. Moreover, the arguments of points of
$\tilde \gamma ^{1/2}_n(z)\subset B(z^1,\rho )$
. Moreover, the arguments of points of
 $\gamma ^{1/2}_n(z)$
lie in one ‘window’ of
$\gamma ^{1/2}_n(z)$
lie in one ‘window’ of
 $s_{n,j}$
while the arguments of points of
$s_{n,j}$
while the arguments of points of
 $\tilde \gamma ^{1/2}_n(x)$
lie in the other ‘window’ of
$\tilde \gamma ^{1/2}_n(x)$
lie in the other ‘window’ of
 $s_{n,j}$
.
$s_{n,j}$
. -
(ii)
 $\gamma ^{1/2}_n(z)$
and
$\gamma ^{1/2}_n(z)$
and
 $\tilde \gamma ^{1/2}_n(z)$
converge to a common point
$\tilde \gamma ^{1/2}_n(z)$
converge to a common point
 $\alpha ^*_{n,j}$
which is a fixed point of
$\alpha ^*_{n,j}$
which is a fixed point of
 $f^{p_n}:f^j(J_n)\to f^j(J_n)$
(that is,
$f^{p_n}:f^j(J_n)\to f^j(J_n)$
(that is,
 $\alpha ^*_{n,j}$
is either the non-separating fixed point
$\alpha ^*_{n,j}$
is either the non-separating fixed point
 $\beta _{n,j}$
or the separating fixed point
$\beta _{n,j}$
or the separating fixed point
 $\alpha _{n,j}$
.
$\alpha _{n,j}$
. -
(iii) The starting points of
 $\gamma ^{1/2}_n(z), \tilde \gamma ^{1/2}_n(z)$
have equal Green level. which is bigger than
$\gamma ^{1/2}_n(z), \tilde \gamma ^{1/2}_n(z)$
have equal Green level. which is bigger than
 $\tilde C_3$
.
$\tilde C_3$
. -
(iv)
 $z^k-\alpha ^*_{n,j}\to 0$
,
$z^k-\alpha ^*_{n,j}\to 0$
,
 $0\le k\le 3$
, as
$0\le k\le 3$
, as
 $n\to \infty $
.
$n\to \infty $
.
Proof. As
![]() $z\in E_\epsilon $
, the lengths of the ‘windows’ of
$z\in E_\epsilon $
, the lengths of the ‘windows’ of
![]() $s_{n,j_n(z)}$
tend uniformly to zero as
$s_{n,j_n(z)}$
tend uniformly to zero as
![]() $n\to \infty $
. It follows from the definition of friendly and unfriendly points that
$n\to \infty $
. It follows from the definition of friendly and unfriendly points that
![]() $t(z^0),t(z^2)$
are in one ‘window’ of
$t(z^0),t(z^2)$
are in one ‘window’ of
![]() $s_{n,j}$
and
$s_{n,j}$
and
![]() $t(z^1),t(z^3)$
are in the other ‘window’ of
$t(z^1),t(z^3)$
are in the other ‘window’ of
![]() $s_{n,j}$
. Therefore, condition (I) of Lemma 4.3 holds for each pair
$s_{n,j}$
. Therefore, condition (I) of Lemma 4.3 holds for each pair
![]() $z^0,z^2$
and
$z^0,z^2$
and
![]() $z^1,z^3$
. Now, apply Lemma 4.3 to
$z^1,z^3$
. Now, apply Lemma 4.3 to
![]() $z\in E_{\epsilon ,p_n,3}$
, first with
$z\in E_{\epsilon ,p_n,3}$
, first with
![]() $i=0$
,
$i=0$
,
![]() $j=2$
, and then with
$j=2$
, and then with
![]() $i=1$
,
$i=1$
,
![]() $j=3$
. Let
$j=3$
. Let
![]() $\gamma ^{1/2}_n(z)=\gamma _{p_n,3,0,2}(z)$
and
$\gamma ^{1/2}_n(z)=\gamma _{p_n,3,0,2}(z)$
and
![]() $\tilde \gamma ^{1/2}_n(z)=\gamma _{p_n,3,1,3}(z)$
. Then (i) and (iii) hold. To check (ii), note that these curves converge to some points
$\tilde \gamma ^{1/2}_n(z)=\gamma _{p_n,3,1,3}(z)$
. Then (i) and (iii) hold. To check (ii), note that these curves converge to some points
![]() $\alpha ,\tilde \alpha \in f^j(J_n)$
which are fixed by
$\alpha ,\tilde \alpha \in f^j(J_n)$
which are fixed by
![]() $f^{2p_n}$
On the other hand, since the rotation number of
$f^{2p_n}$
On the other hand, since the rotation number of
![]() $\alpha _n$
is
$\alpha _n$
is
![]() $1/2$
,
$1/2$
,
![]() $f^{p_n}:f^j(J_n)\to f^j(J_n)$
has no
$f^{p_n}:f^j(J_n)\to f^j(J_n)$
has no
![]() $2$
-cycle. Therefore, one must have either
$2$
-cycle. Therefore, one must have either
![]() $\alpha =\tilde \alpha =\beta _{n,j}$
or
$\alpha =\tilde \alpha =\beta _{n,j}$
or
![]() $\alpha =\tilde \alpha =\alpha _{n,j}$
, that is, (ii) holds too. As
$\alpha =\tilde \alpha =\alpha _{n,j}$
, that is, (ii) holds too. As
![]() $t(z^0)-t(z^2)\to 0$
and
$t(z^0)-t(z^2)\to 0$
and
![]() $t(z^1)-t(z^3)\to 0$
as
$t(z^1)-t(z^3)\to 0$
as
![]() $n\to \infty $
,
$n\to \infty $
,
![]() $z^0-z^2, z^1-z^3\to 0$
also, by Lemma 4.1. Besides, by (4.1),
$z^0-z^2, z^1-z^3\to 0$
also, by Lemma 4.1. Besides, by (4.1),
![]() $z^2-\alpha , z^3-\tilde \alpha \to 0$
as
$z^2-\alpha , z^3-\tilde \alpha \to 0$
as
![]() $n\to \infty $
. As
$n\to \infty $
. As
![]() $\alpha =\tilde \alpha =\alpha ^*_{n,j}$
, (iv) also follows.
$\alpha =\tilde \alpha =\alpha ^*_{n,j}$
, (iv) also follows.
The following lemma is a consequence of Lemmas 4.3 and 4.7.
Lemma 4.8. Let
![]() $n>\tilde n$
. Assume that
$n>\tilde n$
. Assume that
![]() $f^{p_n}$
is satellite and doubling, that is,
$f^{p_n}$
is satellite and doubling, that is,
![]() $\beta _n=\alpha _{n-1}$
and the rotation number of
$\beta _n=\alpha _{n-1}$
and the rotation number of
![]() $\alpha _{n-1}$
is equal to
$\alpha _{n-1}$
is equal to
![]() $1/2$
(in particular,
$1/2$
(in particular,
![]() $p_n=2p_{n-1}$
). For some
$p_n=2p_{n-1}$
). For some
![]() $1\le j\le p_{n-1}$
, denote
$1\le j\le p_{n-1}$
, denote
![]() $J:=f^j(J_{n-1})$
. Let
$J:=f^j(J_{n-1})$
. Let
![]() $J^1:=f^j(J_{n})$
,
$J^1:=f^j(J_{n})$
,
![]() $J^0:=f^{j+p_{n-1}}(J_{n})$
be the two small Julia sets of the next level n which are contained in J (note that
$J^0:=f^{j+p_{n-1}}(J_{n})$
be the two small Julia sets of the next level n which are contained in J (note that
![]() $J^0$
contains the critical point and
$J^0$
contains the critical point and
![]() $J^1$
contains the critical value of the map
$J^1$
contains the critical value of the map
![]() $F:=f^{p_{n-1}}: J\to J)$
. Let
$F:=f^{p_{n-1}}: J\to J)$
. Let
![]() $x\in J^1\cap E_\epsilon $
be such that all five of its forward iterates
$x\in J^1\cap E_\epsilon $
be such that all five of its forward iterates
![]() $x_{kp_{n-1}}=F^k(x)\in E_\epsilon $
,
$x_{kp_{n-1}}=F^k(x)\in E_\epsilon $
,
![]() $k=1,2,3,4,5$
. Then there exist two simple semi-open curves
$k=1,2,3,4,5$
. Then there exist two simple semi-open curves
![]() $\Gamma _n^{1/2}(x)$
,
$\Gamma _n^{1/2}(x)$
,
![]() $\Gamma _n^{1/2}(x)$
consisting of arcs of rays and equipotentials that satisfy essentially conclusions of the previous lemma where n is replaced by
$\Gamma _n^{1/2}(x)$
consisting of arcs of rays and equipotentials that satisfy essentially conclusions of the previous lemma where n is replaced by
![]() $n-1$
, that is, the following statements hold.
$n-1$
, that is, the following statements hold.
-
(i)
 $\Gamma ^{1/2}_n(x), \tilde \Gamma ^{1/2}_n(x)\subset B(x,3/2\rho )$
. Moreover, the arguments of points of
$\Gamma ^{1/2}_n(x), \tilde \Gamma ^{1/2}_n(x)\subset B(x,3/2\rho )$
. Moreover, the arguments of points of
 $\Gamma ^{1/2}_n(x)$
lie in one ‘window’ of
$\Gamma ^{1/2}_n(x)$
lie in one ‘window’ of
 $s_{n-1,j_{n-1}(x)}$
while the arguments of points of
$s_{n-1,j_{n-1}(x)}$
while the arguments of points of
 $\tilde \Gamma ^{1/2}_n(x)$
lie in the other ‘window’ of
$\tilde \Gamma ^{1/2}_n(x)$
lie in the other ‘window’ of
 $s_{n-1,j_{n-1}(x)}$
.
$s_{n-1,j_{n-1}(x)}$
. -
(ii)
 $\Gamma ^{1/2}_n(x)$
and
$\Gamma ^{1/2}_n(x)$
and
 $\tilde \Gamma ^{1/2}_n(x)$
converge to a common point
$\tilde \Gamma ^{1/2}_n(x)$
converge to a common point
 $\beta ^*_{n-1,j_{n-1}(x)}$
which is a fixed point of
$\beta ^*_{n-1,j_{n-1}(x)}$
which is a fixed point of
 $f^{p_{n-1}}: f^j(J_{n-1})\to f^j(J_{n-1})$
(that is,
$f^{p_{n-1}}: f^j(J_{n-1})\to f^j(J_{n-1})$
(that is,
 $\beta ^*_{n-1,j_{n-1}(x)}$
is either the non-separating fixed point
$\beta ^*_{n-1,j_{n-1}(x)}$
is either the non-separating fixed point
 $\beta _{n-1,j_{n-1}(x)}$
or the separating fixed point
$\beta _{n-1,j_{n-1}(x)}$
or the separating fixed point
 $\alpha _{n-1,j_{n-1}(x)}$
.
$\alpha _{n-1,j_{n-1}(x)}$
. -
(iii) The starting points of
 $\Gamma ^{1/2}_n(x), \tilde \Gamma ^{1/2}_n(x)$
have equal Green level which is bigger than
$\Gamma ^{1/2}_n(x), \tilde \Gamma ^{1/2}_n(x)$
have equal Green level which is bigger than
 $\tilde C_3$
.
$\tilde C_3$
. -
(iv)
 $x_{k p_{n-1}}-\beta ^*_{n-1,j_{n-1}(x)}\to 0$
,
$x_{k p_{n-1}}-\beta ^*_{n-1,j_{n-1}(x)}\to 0$
,
 $0\le k\le 3$
as
$0\le k\le 3$
as
 $n\to \infty $
uniformly in x.
$n\to \infty $
uniformly in x.
Remark 4.9. The condition
![]() $F^k(x){\kern-1pt}\in{\kern-1pt} E_\epsilon $
,
$F^k(x){\kern-1pt}\in{\kern-1pt} E_\epsilon $
,
![]() $0{\kern-1pt}\le{\kern-1pt} k{\kern-1pt}\le{\kern-1pt} 5$
, is equivalent to
$0{\kern-1pt}\le{\kern-1pt} k{\kern-1pt}\le{\kern-1pt} 5$
, is equivalent to
![]() $x{\kern-1pt}\in{\kern-1pt} f^{-5p_{n-1}}(E_{\epsilon ,p_{n-1},6})$
.
$x{\kern-1pt}\in{\kern-1pt} f^{-5p_{n-1}}(E_{\epsilon ,p_{n-1},6})$
.
Proof. To fix the idea, let us replace
![]() $f^{p_{n-1}}: f^j(J_{n-1})\to f^j(J_{n-1})$
, using a conjugacy to a quadratic polynomial, by a quadratic polynomial (also denoted by F) so that now
$f^{p_{n-1}}: f^j(J_{n-1})\to f^j(J_{n-1})$
, using a conjugacy to a quadratic polynomial, by a quadratic polynomial (also denoted by F) so that now
![]() $F:J\to J$
where
$F:J\to J$
where
![]() $J=J(F)$
and
$J=J(F)$
and
![]() $F^2$
is satellite with two small Julia sets
$F^2$
is satellite with two small Julia sets
![]() $J^0$
,
$J^0$
,
![]() $J^1$
that meet at the
$J^1$
that meet at the
![]() $\alpha $
-fixed point of F and rays of arguments
$\alpha $
-fixed point of F and rays of arguments
![]() $1/3$
,
$1/3$
,
![]() $2/3$
land at
$2/3$
land at
![]() $\alpha $
. Here
$\alpha $
. Here
![]() $0\in J^0$
,
$0\in J^0$
,
![]() $F(0)\in J^1$
,
$F(0)\in J^1$
,
![]() $F: J^1\to J^0$
is a homeomorphism, while
$F: J^1\to J^0$
is a homeomorphism, while
![]() $F:J^0\to J^1$
is a two-to-one map. If a ray
$F:J^0\to J^1$
is a two-to-one map. If a ray
![]() $R_t$
of F has its accumulation set in
$R_t$
of F has its accumulation set in
![]() $J^1$
then
$J^1$
then
![]() $t\in [1/3,5/12]\cup [7/12,2/3]$
and if
$t\in [1/3,5/12]\cup [7/12,2/3]$
and if
![]() $R_t$
accumulates in
$R_t$
accumulates in
![]() $J^0$
then
$J^0$
then
![]() $t\in [1/6,1/3]\cup [2/3,5/6]$
. This implies that if
$t\in [1/6,1/3]\cup [2/3,5/6]$
. This implies that if
![]() $R_t$
lands at
$R_t$
lands at
![]() $x\in J^1$
and t lies in one of the two ‘windows’
$x\in J^1$
and t lies in one of the two ‘windows’
![]() $[0,1/2)$
,
$[0,1/2)$
,
![]() $(1/2, 1]$
then
$(1/2, 1]$
then
![]() $R_{\sigma (t)}$
lands at
$R_{\sigma (t)}$
lands at
![]() $J^0$
where
$J^0$
where
![]() $\sigma (t)$
must be in a different ‘window’ (in other words, the points of
$\sigma (t)$
must be in a different ‘window’ (in other words, the points of
![]() $J^0$
are ‘unfriendly’). Returning to
$J^0$
are ‘unfriendly’). Returning to
![]() $f^{p_{n-1}}$
, this means, for
$f^{p_{n-1}}$
, this means, for
![]() $x\in J^1$
, that
$x\in J^1$
, that
![]() $t(x),t(F(x))$
are always in different components (where by ‘component’ we mean a component of
$t(x),t(F(x))$
are always in different components (where by ‘component’ we mean a component of
![]() $s_{n-1,j}$
). Besides, for
$s_{n-1,j}$
). Besides, for
![]() $y\in J_\infty \cap J$
, y and
$y\in J_\infty \cap J$
, y and
![]() $F(y)$
are always in different
$F(y)$
are always in different
![]() $J^i$
,
$J^i$
,
![]() $i=0,1$
. This leaves us with just the following possibilities.
$i=0,1$
. This leaves us with just the following possibilities.
-
(i)
 $t(F(x)), t(F^2(x))$
are in different components. This implies that
$t(F(x)), t(F^2(x))$
are in different components. This implies that
 $t(x), t(F(x))$
are in different components and
$t(x), t(F(x))$
are in different components and
 $t(F(x)), t(F^2(x))$
are in different components, that is, points
$t(F(x)), t(F^2(x))$
are in different components, that is, points
 $F^3(x), F^2(x), F(x)$
are all unfriendly.
$F^3(x), F^2(x), F(x)$
are all unfriendly. -
(ii)
 $t(F(x)), t(F^2(x))$
are in the same components. There are two subcases.
$t(F(x)), t(F^2(x))$
are in the same components. There are two subcases. -
(ii′)
 $t(F^3(x)), t(F^4(x))$
are in different components, that is, (i) holds with x replaced by
$t(F^3(x)), t(F^4(x))$
are in different components, that is, (i) holds with x replaced by
 $F^2(x)$
, which implies that
$F^2(x)$
, which implies that
 $F^5(x), F^4(x), F^3(x)$
are all unfriendly.
$F^5(x), F^4(x), F^3(x)$
are all unfriendly. -
(ii″)
 $t(F^3(x)), t(F^4(x))$
are in the same component which then means that
$t(F^3(x)), t(F^4(x))$
are in the same component which then means that
 $F^2(x)$
and
$F^2(x)$
and
 $F^4(x)$
are both friendly.
$F^4(x)$
are both friendly.
In cases (i) and (ii
![]() $^\prime $
), apply Lemma 4.7 with
$^\prime $
), apply Lemma 4.7 with
![]() $n-1$
instead of n to
$n-1$
instead of n to
![]() $z=F^3(x)$
and to
$z=F^3(x)$
and to
![]() $z=F^5(x)$
, respectively, letting
$z=F^5(x)$
, respectively, letting
![]() $\Gamma ^{1/2}_n(x)=\gamma ^{1/2}_{n-1}(F^3(x))$
,
$\Gamma ^{1/2}_n(x)=\gamma ^{1/2}_{n-1}(F^3(x))$
,
![]() $\tilde \Gamma ^{1/2}_n(x)=\tilde \gamma ^{1/2}_{n-1}(F^3(x))$
and
$\tilde \Gamma ^{1/2}_n(x)=\tilde \gamma ^{1/2}_{n-1}(F^3(x))$
and
![]() $\Gamma ^{1/2}_n(x)=\gamma ^{1/2}_{n-1}(F^5(x))$
,
$\Gamma ^{1/2}_n(x)=\gamma ^{1/2}_{n-1}(F^5(x))$
,
![]() $\tilde \Gamma ^{1/2}_n(x)=\tilde \gamma ^{1/2}_{n-1}(F^5(x))$
, respectively. In case (ii
$\tilde \Gamma ^{1/2}_n(x)=\tilde \gamma ^{1/2}_{n-1}(F^5(x))$
, respectively. In case (ii
![]() $^{\prime \prime }$
), apply Lemma 4.3 with
$^{\prime \prime }$
), apply Lemma 4.3 with
![]() $p_{n-1}$
,
$p_{n-1}$
,
![]() $q=1$
,
$q=1$
,
![]() $i=0,j=0$
, first to the point
$i=0,j=0$
, first to the point
![]() $F^2(x)$
and then to the point
$F^2(x)$
and then to the point
![]() $F^4(x)$
, letting
$F^4(x)$
, letting
![]() $\Gamma ^{1/2}_n(x)=\gamma _{p_{n-1},1,0,1}(F^2(x))$
,
$\Gamma ^{1/2}_n(x)=\gamma _{p_{n-1},1,0,1}(F^2(x))$
,
![]() $\tilde \Gamma ^{1/2}_n(x)=\gamma _{p_{n-1},1,0,1}(F^4(x))$
.
$\tilde \Gamma ^{1/2}_n(x)=\gamma _{p_{n-1},1,0,1}(F^4(x))$
.
5. Proof of Theorem 1.1
Every invariant probability measure with positive Lyapunov exponent has an ergodic component with positive exponent. So let
![]() $\mu $
be such an ergodic f-invariant measure component supported in
$\mu $
be such an ergodic f-invariant measure component supported in
![]() $J_\infty $
. First, we have the following general remark.
$J_\infty $
. First, we have the following general remark.
Remark 5.1. Given
![]() $x\in J^{\prime }_\infty $
such that
$x\in J^{\prime }_\infty $
such that
![]() $\tilde r(x)>0$
as in Proposition 2.3, and given n, the set
$\tilde r(x)>0$
as in Proposition 2.3, and given n, the set
![]() $J_{n,x}=f^{j_n(x)}(J_n)$
cannot be covered by
$J_{n,x}=f^{j_n(x)}(J_n)$
cannot be covered by
![]() $B(x,\tilde r(x))$
because otherwise the branch
$B(x,\tilde r(x))$
because otherwise the branch
![]() $g_{p_n}: B(x,\tilde r(x))\to \mathbb {C}$
of
$g_{p_n}: B(x,\tilde r(x))\to \mathbb {C}$
of
![]() $f^{-p_n}$
, which sends x to
$f^{-p_n}$
, which sends x to
![]() $x_{-p_n}\in J_{n,x}$
, meets the critical value along the way so cannot be well defined. Thus
$x_{-p_n}\in J_{n,x}$
, meets the critical value along the way so cannot be well defined. Thus
![]() $\operatorname {\mathrm {diam}} J_{n,x}>\tilde r(x)$
, for each n, and
$\operatorname {\mathrm {diam}} J_{n,x}>\tilde r(x)$
, for each n, and
![]() $\operatorname {\mathrm {diam}} K_x=\lim \operatorname {\mathrm {diam}} J_{n,x}\ge \tilde r(x)$
. In particular,
$\operatorname {\mathrm {diam}} K_x=\lim \operatorname {\mathrm {diam}} J_{n,x}\ge \tilde r(x)$
. In particular,
![]() $\operatorname {\mathrm {diam}} J_{n,x}\ge r(\epsilon )$
for all
$\operatorname {\mathrm {diam}} J_{n,x}\ge r(\epsilon )$
for all
![]() $x\in E_\epsilon $
and n.
$x\in E_\epsilon $
and n.
We need to prove that f has finitely many satellite renormalizations. Assuming the contrary, let
![]() $\mathcal {S}$
be an infinite subsequence such that
$\mathcal {S}$
be an infinite subsequence such that
![]() $f^{p_n}$
is a satellite renormalization of f for each
$f^{p_n}$
is a satellite renormalization of f for each
![]() $n\in \mathcal {S}$
.
$n\in \mathcal {S}$
.
We arrive at a contradiction by considering, roughly speaking, two alternative situations. In the first one, we find a point
![]() $x\in E_\epsilon $
, n, and two curves in
$x\in E_\epsilon $
, n, and two curves in
![]() $B\cap A(\infty )$
where
$B\cap A(\infty )$
where
![]() $B:=B(x,\tilde r(x))$
that tend to the
$B:=B(x,\tilde r(x))$
that tend to the
![]() $\beta $
-fixed points of
$\beta $
-fixed points of
![]() $J_{n,x}$
such that the other ends of the curves can be joined by an arc of equipotential in B, thus ‘surrounding’
$J_{n,x}$
such that the other ends of the curves can be joined by an arc of equipotential in B, thus ‘surrounding’
![]() $J_{n,x}$
by a ‘triangle’ in B which would be a contradiction as in Remark 5.1. The second situation is when the first one does not occur. Then we use several curves to ‘surround’
$J_{n,x}$
by a ‘triangle’ in B which would be a contradiction as in Remark 5.1. The second situation is when the first one does not occur. Then we use several curves to ‘surround’
![]() $J_{n,x}$
by a ‘quadrilateral’ in B, ending by the same conclusion. The curves we use have been constructed in Lemmas 4.5 and 4.8.
$J_{n,x}$
by a ‘quadrilateral’ in B, ending by the same conclusion. The curves we use have been constructed in Lemmas 4.5 and 4.8.
The first situation happens in cases A and B1 below, and the second one in B2, see Figure 2.

Figure 2 Left: cases A and B1. Right: case B2.
Case A:
![]() $\mathcal {S}$
contains an infinite sequence of indices of non-doubling renormalizations. Passing to a subsequence, one can assume that
$\mathcal {S}$
contains an infinite sequence of indices of non-doubling renormalizations. Passing to a subsequence, one can assume that
![]() $f^{p_n}$
is satellite and not doubling for every
$f^{p_n}$
is satellite and not doubling for every
![]() $n\in \mathcal {S}$
.
$n\in \mathcal {S}$
.
Fix
![]() $\zeta =1/4$
. By Lemma 2.2, for each
$\zeta =1/4$
. By Lemma 2.2, for each
![]() $n\in \mathcal {S}$
and each
$n\in \mathcal {S}$
and each
![]() $j=1,\ldots ,[\zeta p_n]$
, the map
$j=1,\ldots ,[\zeta p_n]$
, the map
![]() $\sigma ^{j-1}:S_{n,1}\to S_{n,j}$
is a homeomorphism and the length
$\sigma ^{j-1}:S_{n,1}\to S_{n,j}$
is a homeomorphism and the length
![]() $|S_{n,j}|\to 0$
as
$|S_{n,j}|\to 0$
as
![]() $n\to \infty $
uniformly in j. Fix N such that
$n\to \infty $
uniformly in j. Fix N such that
![]() $|S_{n,j}|<\delta $
for each
$|S_{n,j}|<\delta $
for each
![]() $n>N$
,
$n>N$
,
![]() $n\in \mathcal {S}$
. For
$n\in \mathcal {S}$
. For
![]() $n\in \mathcal {S}$
, let
$n\in \mathcal {S}$
, let
Let
![]() $n,m\in \mathcal {S}$
,
$n,m\in \mathcal {S}$
,
![]() $m<n$
. Denote
$m<n$
. Denote
![]() $p=p_m, \tilde p =p_n$
,
$p=p_m, \tilde p =p_n$
,
![]() $q=p_n/p_m$
. The intersection
$q=p_n/p_m$
. The intersection
![]() $\mathcal {C}_n\cap \mathcal {C}_m$
contains all
$\mathcal {C}_n\cap \mathcal {C}_m$
contains all
![]() $f^{j+kp}(J_n)$
with
$f^{j+kp}(J_n)$
with
![]() $1\le j\le [\zeta p]$
,
$1\le j\le [\zeta p]$
,
![]() $j+kp\le [\zeta \tilde p]$
. Hence,
$j+kp\le [\zeta \tilde p]$
. Hence,
 $$ \begin{align*}\#(\mathcal{C}_n\cap \mathcal{C}_m)&\ge \sum_{j=1}^{[\zeta p]} \bigg[\zeta q - \frac{j}{p}\bigg]\ge [\zeta q-1][\zeta p]\\&\ge\tilde p \bigg(\frac{\zeta p-1}{p} \frac{\zeta q-1}{q}-\frac{\zeta}{q}\bigg)\sim \zeta^2 \tilde p\end{align*} $$
$$ \begin{align*}\#(\mathcal{C}_n\cap \mathcal{C}_m)&\ge \sum_{j=1}^{[\zeta p]} \bigg[\zeta q - \frac{j}{p}\bigg]\ge [\zeta q-1][\zeta p]\\&\ge\tilde p \bigg(\frac{\zeta p-1}{p} \frac{\zeta q-1}{q}-\frac{\zeta}{q}\bigg)\sim \zeta^2 \tilde p\end{align*} $$
as
![]() $p,q\to \infty $
. Therefore, fixing
$p,q\to \infty $
. Therefore, fixing
![]() $\kappa =\zeta ^2/2=1/8$
, there are
$\kappa =\zeta ^2/2=1/8$
, there are
![]() $m_0,k_0$
such that for each
$m_0,k_0$
such that for each
![]() $n,m\in \mathcal {S}$
,
$n,m\in \mathcal {S}$
,
![]() $m>m_0$
,
$m>m_0$
,
![]() $n>m+k_0$
,
$n>m+k_0$
,
Fix such
![]() $n,m$
. Assume also that
$n,m$
. Assume also that
![]() $m>\max \{N, n_*\}$
where
$m>\max \{N, n_*\}$
where
![]() $n_*$
is defined in Lemma 4.5 and recall the set
$n_*$
is defined in Lemma 4.5 and recall the set
 $$ \begin{align*}X_n=E_{\epsilon,p_n,4}\cap E_{\epsilon, p_{n-1},Q}=\bigcap_{i=0}^3 f^{i p_n}(E_\epsilon)\bigcap_{k=0}^{Q-1} f^{k p_{n-1}}(E_\epsilon).\end{align*} $$
$$ \begin{align*}X_n=E_{\epsilon,p_n,4}\cap E_{\epsilon, p_{n-1},Q}=\bigcap_{i=0}^3 f^{i p_n}(E_\epsilon)\bigcap_{k=0}^{Q-1} f^{k p_{n-1}}(E_\epsilon).\end{align*} $$
Since
![]() $\mu (X_n)>1-(Q+4)\epsilon >1-\kappa $
, there is
$\mu (X_n)>1-(Q+4)\epsilon >1-\kappa $
, there is
![]() $x\in X_n\cap \mathcal {C}_n\cap \mathcal {C}_m$
and, by the choice of n, the assumption (II) of Lemma 4.5 holds for x. Therefore, there exist two simple semi-open curves
$x\in X_n\cap \mathcal {C}_n\cap \mathcal {C}_m$
and, by the choice of n, the assumption (II) of Lemma 4.5 holds for x. Therefore, there exist two simple semi-open curves
![]() $\gamma (x)$
and
$\gamma (x)$
and
![]() $\tilde \gamma (x)$
that satisfy the following properties:
$\tilde \gamma (x)$
that satisfy the following properties:
![]() $\gamma (x)$
and
$\gamma (x)$
and
![]() $\tilde \gamma (x)$
tend to
$\tilde \gamma (x)$
tend to
![]() $\beta _{n,j_n(x)}$
,
$\beta _{n,j_n(x)}$
,
![]() $\gamma (x), \tilde \gamma (x)\subset B(x, \rho )\cap A(\infty )$
, and
$\gamma (x), \tilde \gamma (x)\subset B(x, \rho )\cap A(\infty )$
, and
![]() $\gamma (x), \tilde \gamma (x)$
consist of arcs of equipotentials and external rays; the starting point
$\gamma (x), \tilde \gamma (x)$
consist of arcs of equipotentials and external rays; the starting point
![]() $b_1$
of
$b_1$
of
![]() $\gamma (x)$
and the starting point
$\gamma (x)$
and the starting point
![]() $\tilde b_1$
of
$\tilde b_1$
of
![]() $\tilde \gamma (x)$
have equal levels which is at least
$\tilde \gamma (x)$
have equal levels which is at least
![]() $\tilde C/4$
;
$\tilde C/4$
;
![]() $\gamma (x)$
,
$\gamma (x)$
,
![]() $\tilde \gamma (x)\subset U_{n-1, j_{n-1}(x)}$
; finally, being completed by their common limit point
$\tilde \gamma (x)\subset U_{n-1, j_{n-1}(x)}$
; finally, being completed by their common limit point
![]() $\beta _{n,j_n(x)}$
and arcs of rays from
$\beta _{n,j_n(x)}$
and arcs of rays from
![]() $b_1\in \gamma (x)$
to
$b_1\in \gamma (x)$
to
![]() $\infty $
and from
$\infty $
and from
![]() $\tilde b_1\in \tilde \gamma (x)$
to
$\tilde b_1\in \tilde \gamma (x)$
to
![]() $\infty $
, they split the plane into two domains such that one of them contains
$\infty $
, they split the plane into two domains such that one of them contains
![]() $I:=J_{n,x}\setminus \beta _{n,j_n(x)}$
and the other one contains all other iterates
$I:=J_{n,x}\setminus \beta _{n,j_n(x)}$
and the other one contains all other iterates
![]() $f^{kp_{n-1}}(I)$
,
$f^{kp_{n-1}}(I)$
,
![]() $1\le k\le q_n-1$
. Now, since
$1\le k\le q_n-1$
. Now, since
![]() $U_{n-1, j_{n-1}(x)}\subset U_{m, j_{m}(x)}$
and by the choice of m, the distance between the arguments of the points
$U_{n-1, j_{n-1}(x)}\subset U_{m, j_{m}(x)}$
and by the choice of m, the distance between the arguments of the points
![]() $b_1$
and
$b_1$
and
![]() $\tilde b_1$
inside of
$\tilde b_1$
inside of
![]() $S_{n-1,j_{n-1}(x)}$
is less than
$S_{n-1,j_{n-1}(x)}$
is less than
![]() $\delta $
. By the definition of
$\delta $
. By the definition of
![]() $\delta $
,
$\delta $
,
![]() $b_1$
and
$b_1$
and
![]() $\tilde b_1$
can be joined by an arc
$\tilde b_1$
can be joined by an arc
![]() $A_n$
of equipotential inside of
$A_n$
of equipotential inside of
![]() $B(x,\rho )\cap U_{n-1, j_{n-1}(x)}$
. Consider a Jordan domain
$B(x,\rho )\cap U_{n-1, j_{n-1}(x)}$
. Consider a Jordan domain
![]() $Z_n$
with the boundary consisting of the arc
$Z_n$
with the boundary consisting of the arc
![]() $A_n$
and semi-open curves
$A_n$
and semi-open curves
![]() $\gamma (x)$
,
$\gamma (x)$
,
![]() $\tilde \gamma (x)$
completed by their common limit point
$\tilde \gamma (x)$
completed by their common limit point
![]() $\beta _{n,j_n(x)}$
. Then
$\beta _{n,j_n(x)}$
. Then
![]() $Z_n\subset B(x,\rho )$
. By the properties of the curves,
$Z_n\subset B(x,\rho )$
. By the properties of the curves,
![]() $Z_n\cup \beta _{n,j_n(x)}$
contains either
$Z_n\cup \beta _{n,j_n(x)}$
contains either
![]() $J_{n,x}$
or its iterate
$J_{n,x}$
or its iterate
![]() $f^{kp_{n-1}}(J_{n,x})$
, for some
$f^{kp_{n-1}}(J_{n,x})$
, for some
![]() $1\le k\le q_n-1$
, in a contradiction with Remark 5.1.
$1\le k\le q_n-1$
, in a contradiction with Remark 5.1.
We now turn to the complement to case A.
Case B: for all big n, every satellite renormalization
![]() $f^{p_n}$
is doubling, that is,
$f^{p_n}$
is doubling, that is,
![]() $\beta _n=\alpha _{n-1}$
and
$\beta _n=\alpha _{n-1}$
and
![]() $p_n=2p_{n-1}$
for every
$p_n=2p_{n-1}$
for every
![]() $n\in \mathcal {S}$
. Let
$n\in \mathcal {S}$
. Let
![]() $Y_{n-1}=E_{\epsilon ,p_{n-1},6}$
and
$Y_{n-1}=E_{\epsilon ,p_{n-1},6}$
and
![]() $\tilde Y_{n-1}=f^{-5p_{n-1}}(Y_{n-1})$
. Note that
$\tilde Y_{n-1}=f^{-5p_{n-1}}(Y_{n-1})$
. Note that
![]() $\mu (Y_{n-1})=\mu (\tilde Y_{n-1})>1-6\epsilon $
.
$\mu (Y_{n-1})=\mu (\tilde Y_{n-1})>1-6\epsilon $
.
For every
![]() $n\in \mathcal {S}$
, let
$n\in \mathcal {S}$
, let
 $$ \begin{align*}L_{n}=\bigg\{0<j<p_{n-1}| \mu(f^j(J_{n-1})\cap \tilde Y_{n-1})>\frac{1-2^{12}\epsilon}{p_{n-1}}\bigg\}.\end{align*} $$
$$ \begin{align*}L_{n}=\bigg\{0<j<p_{n-1}| \mu(f^j(J_{n-1})\cap \tilde Y_{n-1})>\frac{1-2^{12}\epsilon}{p_{n-1}}\bigg\}.\end{align*} $$
As
![]() $\mu (\tilde Y_{n-1})>1-6\epsilon $
, it follows that
$\mu (\tilde Y_{n-1})>1-6\epsilon $
, it follows that
Since we are in case B, each
![]() $f^j(J_{n-1})$
contains precisely two small Julia sets
$f^j(J_{n-1})$
contains precisely two small Julia sets
![]() $f^j(J_n),f^{j+p_{n-1}}(J_n)$
of the next level n, each of them of measure
$f^j(J_n),f^{j+p_{n-1}}(J_n)$
of the next level n, each of them of measure
![]() $1/(2p_{n-1})$
. Hence, the measure of intersection of each of these small Julia sets with
$1/(2p_{n-1})$
. Hence, the measure of intersection of each of these small Julia sets with
![]() $\tilde Y_{n-1}$
is bigger than
$\tilde Y_{n-1}$
is bigger than
![]() $(1/2-2^{10}\epsilon )/p_{n-1}>0$
. By Lemma 4.8, choosing for every
$(1/2-2^{10}\epsilon )/p_{n-1}>0$
. By Lemma 4.8, choosing for every
![]() $j\in L_n$
a point
$j\in L_n$
a point
![]() $x_j\in f^j(J_{n-1})\cap \tilde Y_{n-1}$
, we get a pair of curves
$x_j\in f^j(J_{n-1})\cap \tilde Y_{n-1}$
, we get a pair of curves
![]() $\Gamma ^{1/2}_{n}(x_j),\tilde \Gamma ^{1/2}_n(x_j)$
consisting of arcs of rays and equipotentials as follows. (i)
$\Gamma ^{1/2}_{n}(x_j),\tilde \Gamma ^{1/2}_n(x_j)$
consisting of arcs of rays and equipotentials as follows. (i)
![]() $\Gamma ^{1/2}_{n}(x_j), \tilde \Gamma ^{1/2}_{n}(x_j)\subset B(x_j,3/2\rho )$
. Moreover, arguments of points of
$\Gamma ^{1/2}_{n}(x_j), \tilde \Gamma ^{1/2}_{n}(x_j)\subset B(x_j,3/2\rho )$
. Moreover, arguments of points of
![]() $\Gamma ^{1/2}_{n}(x_j)$
lie in one ‘window’ of
$\Gamma ^{1/2}_{n}(x_j)$
lie in one ‘window’ of
![]() $s_{n-1,j}$
while arguments of points of
$s_{n-1,j}$
while arguments of points of
![]() $\tilde \Gamma ^{1/2}_{n}(x_j)$
lie in another ‘window’ of
$\tilde \Gamma ^{1/2}_{n}(x_j)$
lie in another ‘window’ of
![]() $s_{n-1,j}$
. (ii)
$s_{n-1,j}$
. (ii)
![]() $\Gamma ^{1/2}_{n}(x_j)$
and
$\Gamma ^{1/2}_{n}(x_j)$
and
![]() $\tilde \Gamma ^{1/2}_{n}(x_j)$
converge to a common point
$\tilde \Gamma ^{1/2}_{n}(x_j)$
converge to a common point
![]() $\beta ^*_{n-1,j}$
which is a fixed point of
$\beta ^*_{n-1,j}$
which is a fixed point of
![]() $f^{p_{n-1}}: f^j(J_{n-1})\to f^j(J_{n-1})$
(that is,
$f^{p_{n-1}}: f^j(J_{n-1})\to f^j(J_{n-1})$
(that is,
![]() $\beta ^*_{n-1,j}$
is either the non-separating fixed point
$\beta ^*_{n-1,j}$
is either the non-separating fixed point
![]() $\beta _{n-1,j}$
or the separating fixed point
$\beta _{n-1,j}$
or the separating fixed point
![]() $\alpha _{n-1,j}$
). (iii) The start points of
$\alpha _{n-1,j}$
). (iii) The start points of
![]() $\Gamma ^{1/2}_{n}(x_j), \tilde \Gamma ^{1/2}_{n}(x_j)$
have equal Green level which is bigger than
$\Gamma ^{1/2}_{n}(x_j), \tilde \Gamma ^{1/2}_{n}(x_j)$
have equal Green level which is bigger than
![]() $\tilde C_3$
. (iv)
$\tilde C_3$
. (iv)
![]() $x_{j}-\beta ^*_{n-1,j}\to 0$
as
$x_{j}-\beta ^*_{n-1,j}\to 0$
as
![]() $n\to \infty $
uniformly in j and
$n\to \infty $
uniformly in j and
![]() $x_j$
. We add one more property as follows. Let
$x_j$
. We add one more property as follows. Let
Then (v)
![]() $\Gamma _{n,j}$
is a simple curve; the level of
$\Gamma _{n,j}$
is a simple curve; the level of
![]() $z\in \Gamma _{n,j}\setminus \{\beta ^*_{n-1,j}\}$
is positive and decreases (not strictly) from
$z\in \Gamma _{n,j}\setminus \{\beta ^*_{n-1,j}\}$
is positive and decreases (not strictly) from
![]() $\tilde C_3$
to zero along
$\tilde C_3$
to zero along
![]() $\Gamma ^{1/2}_{n}(x_j)$
and then increases from zero to
$\Gamma ^{1/2}_{n}(x_j)$
and then increases from zero to
![]() $\tilde C_3$
along
$\tilde C_3$
along
![]() $\tilde \Gamma ^{1/2}_{n}(x_j)$
; moreover, if
$\tilde \Gamma ^{1/2}_{n}(x_j)$
; moreover, if
![]() $j_1,j_2\in L_n$
,
$j_1,j_2\in L_n$
,
![]() $j_1\neq j_2$
, then
$j_1\neq j_2$
, then
![]() $\Gamma _{n,1}$
,
$\Gamma _{n,1}$
,
![]() $\Gamma _{n,j_2}$
are either disjoint or meet at the unique common point
$\Gamma _{n,j_2}$
are either disjoint or meet at the unique common point
![]() $\beta _{n-1,j_1}=\beta _{n-1,j_2}$
and then disjoint with all others
$\beta _{n-1,j_1}=\beta _{n-1,j_2}$
and then disjoint with all others
![]() $\gamma _{n-1,j}$
,
$\gamma _{n-1,j}$
,
![]() $j\neq j_1,j_2$
. This is because, by property (i),
$j\neq j_1,j_2$
. This is because, by property (i),
![]() $\Gamma _{n,j}\subset \overline {U_{n-1,j}}$
where (by (C), §2) any two
$\Gamma _{n,j}\subset \overline {U_{n-1,j}}$
where (by (C), §2) any two
![]() $\overline {U_{n-1,j}}$
,
$\overline {U_{n-1,j}}$
,
![]() $\overline {U_{n-1,\tilde j}}$
,
$\overline {U_{n-1,\tilde j}}$
,
![]() $j\neq \tilde j$
, are either disjoint or meet at
$j\neq \tilde j$
, are either disjoint or meet at
![]() $\beta :=\beta _{n-1,j}=\beta _{n-1,\tilde j}$
in which case
$\beta :=\beta _{n-1,j}=\beta _{n-1,\tilde j}$
in which case
![]() $f^{p_{n-1}}$
is satellite. In the case considered, any satellite is doubling so
$f^{p_{n-1}}$
is satellite. In the case considered, any satellite is doubling so
![]() $\beta \neq \beta _{n-1,i}$
for all i different from
$\beta \neq \beta _{n-1,i}$
for all i different from
![]() $j,\tilde j$
.
$j,\tilde j$
.
We assign, for use below, a ‘small’ Julia set
![]() $I_{n,j}$
to each
$I_{n,j}$
to each
![]() $\Gamma _{n,j}$
as follows: by the construction,
$\Gamma _{n,j}$
as follows: by the construction,
![]() $\beta ^*_{n-1,j}$
is either the
$\beta ^*_{n-1,j}$
is either the
![]() $\beta $
-fixed point of
$\beta $
-fixed point of
![]() $f^j(J_{n-1})$
or the
$f^j(J_{n-1})$
or the
![]() $\alpha $
-fixed point of
$\alpha $
-fixed point of
![]() $f^j(J_{n-1})$
. In the former case let
$f^j(J_{n-1})$
. In the former case let
![]() $I_{n,j}=f^j(J_{n-1})$
, and in the latter case
$I_{n,j}=f^j(J_{n-1})$
, and in the latter case
![]() $I_{n,j}=f^j(J_n)$
(one of the two small Julia sets of the next level n that are contained in
$I_{n,j}=f^j(J_n)$
(one of the two small Julia sets of the next level n that are contained in
![]() $f^j(J_{n-1})$
. Observe that
$f^j(J_{n-1})$
. Observe that
![]() $I_{n,j}\cap \Gamma _{n-1,j}=\{\beta ^*_{n-1,j}\}$
and is disjoint with any other
$I_{n,j}\cap \Gamma _{n-1,j}=\{\beta ^*_{n-1,j}\}$
and is disjoint with any other
![]() $\Gamma _{n, j'}$
provided
$\Gamma _{n, j'}$
provided
![]() $\Gamma _{n,j}$
,
$\Gamma _{n,j}$
,
![]() $\Gamma _{n,j'}$
are disjoint.
$\Gamma _{n,j'}$
are disjoint.
There are two subcases B1–B2 to distinguish depending on whether arguments of end points of
![]() $\Gamma _{m,j}$
become close or not. If they do, then one can join the end points of some
$\Gamma _{m,j}$
become close or not. If they do, then one can join the end points of some
![]() $\Gamma _{n,j}$
by an arc of equipotential inside of
$\Gamma _{n,j}$
by an arc of equipotential inside of
![]() $B(x_j,2\rho )\supset \Gamma _{m,j}$
to surround a small Julia set as in case A, which would lead to a contradiction. If they do not, the construction is more subtle: we build a domain (‘quadrilateral’) in
$B(x_j,2\rho )\supset \Gamma _{m,j}$
to surround a small Julia set as in case A, which would lead to a contradiction. If they do not, the construction is more subtle: we build a domain (‘quadrilateral’) in
![]() $B(x_j,2\rho )$
bounded by two disjoint curves as above completed by two arcs of equipotential that join ends of different curve, so that the quadrilateral obtained again contains a small Julia set.
$B(x_j,2\rho )$
bounded by two disjoint curves as above completed by two arcs of equipotential that join ends of different curve, so that the quadrilateral obtained again contains a small Julia set.
Case B1:
![]() $\liminf _{n\in \mathcal {S},j\in L_n}|S_{n-1,j}|<\delta $
. By property (i) listed above and the definition of
$\liminf _{n\in \mathcal {S},j\in L_n}|S_{n-1,j}|<\delta $
. By property (i) listed above and the definition of
![]() $\delta $
, there are a sequence
$\delta $
, there are a sequence
![]() $(n_k)\subset \mathcal {S}$
,
$(n_k)\subset \mathcal {S}$
,
![]() $j_k\in L_{n_k}$
and
$j_k\in L_{n_k}$
and
![]() $x_{j_k}$
as above, such that two ends of each curve
$x_{j_k}$
as above, such that two ends of each curve
![]() $\Gamma _{n_k,j_k}$
can be joined inside of
$\Gamma _{n_k,j_k}$
can be joined inside of
![]() $B(x_{j_k},\rho )$
by an arc
$B(x_{j_k},\rho )$
by an arc
![]() $A^k$
of equipotential of fixed level
$A^k$
of equipotential of fixed level
![]() $\tilde C_3$
such that all arguments of points in
$\tilde C_3$
such that all arguments of points in
![]() $A^k$
belong to
$A^k$
belong to
![]() $S_{n_k-1,j_k}$
. Then we arrive at a contradiction as in case A.
$S_{n_k-1,j_k}$
. Then we arrive at a contradiction as in case A.
Case B2:
![]() $|S_{n-1,j}|\ge \delta $
for all big
$|S_{n-1,j}|\ge \delta $
for all big
![]() $n\in \mathcal {S}$
and all
$n\in \mathcal {S}$
and all
![]() $j\in L_n$
. Fix
$j\in L_n$
. Fix
![]() $n,m\in \mathcal {S}$
,
$n,m\in \mathcal {S}$
,
![]() $m-n\ge 3$
. Define a subset of
$m-n\ge 3$
. Define a subset of
![]() $L_n$
as follows:
$L_n$
as follows:
 $$ \begin{align*}L_{n}^m=\bigg\{0<j<p_{n-1}| \mu(f^j(J_{n-1})\cap (\tilde Y_{n-1}\cap\tilde Y_{m-1}))>\frac{1-2^{12}\epsilon}{p_{n-1}}\bigg\}.\end{align*} $$
$$ \begin{align*}L_{n}^m=\bigg\{0<j<p_{n-1}| \mu(f^j(J_{n-1})\cap (\tilde Y_{n-1}\cap\tilde Y_{m-1}))>\frac{1-2^{12}\epsilon}{p_{n-1}}\bigg\}.\end{align*} $$
As
![]() $\mu (\tilde Y_{n-1}\cap \tilde Y_{m-1})>1-12\epsilon $
,
$\mu (\tilde Y_{n-1}\cap \tilde Y_{m-1})>1-12\epsilon $
,
For each
![]() $j\in L_n^m$
we define further
$j\in L_n^m$
we define further
 $$ \begin{align*}L_{n,j}^m&=\bigg\{0<k<p_{n-1}| f^k(J_{m-1})\\& \qquad \subset f^j(J_{n-1}) , \mu(f^k(J_{m-1})\cap(\tilde Y_{n-1}\cap\tilde Y_{m-1}))>\frac{1-2^{16}\epsilon}{p_{m-1}}\bigg\}. \end{align*} $$
$$ \begin{align*}L_{n,j}^m&=\bigg\{0<k<p_{n-1}| f^k(J_{m-1})\\& \qquad \subset f^j(J_{n-1}) , \mu(f^k(J_{m-1})\cap(\tilde Y_{n-1}\cap\tilde Y_{m-1}))>\frac{1-2^{16}\epsilon}{p_{m-1}}\bigg\}. \end{align*} $$
Then
as otherwise
![]() $\# L_{n,j}^m\le 4$
and therefore
$\# L_{n,j}^m\le 4$
and therefore
 $(1-2^{12}\epsilon )/p_{n-1}<4/p_{m-1}+(p_{m-1}/p_{n-1}-4) (1-2^{16}\epsilon )/p_{m-1}=2^{18}\epsilon /p_{m-1}+(1-2^{16}\epsilon )/p_{n-1}$
, that is,
$(1-2^{12}\epsilon )/p_{n-1}<4/p_{m-1}+(p_{m-1}/p_{n-1}-4) (1-2^{16}\epsilon )/p_{m-1}=2^{18}\epsilon /p_{m-1}+(1-2^{16}\epsilon )/p_{n-1}$
, that is,
![]() $p_{m-1}/p_{n-1}<2^{18}\epsilon /(2^{16}\epsilon -2^{12}\epsilon )=4/(1-2^{-4})<8$
, a contradiction because
$p_{m-1}/p_{n-1}<2^{18}\epsilon /(2^{16}\epsilon -2^{12}\epsilon )=4/(1-2^{-4})<8$
, a contradiction because
![]() $p_{m-1}/p_{n-1}\ge 2^{m-n}\ge 2^3$
.
$p_{m-1}/p_{n-1}\ge 2^{m-n}\ge 2^3$
.
Fix
![]() $j\in L_n^m$
. Thus
$j\in L_n^m$
. Thus
![]() $L_{n,j}^m$
contains five pairwise different indices
$L_{n,j}^m$
contains five pairwise different indices
![]() $k_i$
,
$k_i$
,
![]() $1\le k\le 5$
. As
$1\le k\le 5$
. As
![]() $L_{n,j}^m\subset L_m$
, we find five curves
$L_{n,j}^m\subset L_m$
, we find five curves
![]() $\Gamma _{m-1, k_i}$
. By property (v), if two of them meet, they are disjoint with all others. Therefore, there are at least three of them, denoted by
$\Gamma _{m-1, k_i}$
. By property (v), if two of them meet, they are disjoint with all others. Therefore, there are at least three of them, denoted by
![]() $\Gamma _{m-1,r_i}$
,
$\Gamma _{m-1,r_i}$
,
![]() $i=1,2,3$
, which are pairwise disjoint. Let
$i=1,2,3$
, which are pairwise disjoint. Let
![]() $w_i,\tilde w_{m,i}$
be the two ends of
$w_i,\tilde w_{m,i}$
be the two ends of
![]() $\Gamma _{m-1,r_i}$
.
$\Gamma _{m-1,r_i}$
.
For each
![]() $i=1,2,3$
, the arguments of points of
$i=1,2,3$
, the arguments of points of
![]() $w_{m,i},\tilde w_{m,i}$
lie in different ‘windows’ of
$w_{m,i},\tilde w_{m,i}$
lie in different ‘windows’ of
![]() $s_{m-1,r_i}$
. On the other hand, by the choice of j,
$s_{m-1,r_i}$
. On the other hand, by the choice of j,
![]() $s_{m-1,r_i}\subset s_{n-1,j}\subset S_{n-1,j}$
. As n is big enough, the lengths of the ‘windows’ of
$s_{m-1,r_i}\subset s_{n-1,j}\subset S_{n-1,j}$
. As n is big enough, the lengths of the ‘windows’ of
![]() $s_{n-1,j}$
are less than
$s_{n-1,j}$
are less than
![]() $\delta $
. But since we are in case B2, the length of
$\delta $
. But since we are in case B2, the length of
![]() $S_{n-1,j}$
is bigger than
$S_{n-1,j}$
is bigger than
![]() $\delta $
. One can assume, therefore, that, for
$\delta $
. One can assume, therefore, that, for
![]() $i=1,2,3$
, the arguments of
$i=1,2,3$
, the arguments of
![]() $w_{m,i}$
lie in one window of
$w_{m,i}$
lie in one window of
![]() $s_{n-1,j}$
while the arguments of
$s_{n-1,j}$
while the arguments of
![]() $\tilde w_{m,i}$
are in the other window. Therefore, differences of arguments of all
$\tilde w_{m,i}$
are in the other window. Therefore, differences of arguments of all
![]() $w_{m,i}$
tend to zero as
$w_{m,i}$
tend to zero as
![]() $m\to \infty $
, and the same for
$m\to \infty $
, and the same for
![]() $\tilde w_{m,i}$
. As all
$\tilde w_{m,i}$
. As all
![]() $w_{m,i},\tilde w_{m,i}\in E_\epsilon $
, this implies by Lemma 4.1 that
$w_{m,i},\tilde w_{m,i}\in E_\epsilon $
, this implies by Lemma 4.1 that
![]() ${\max _{1\le i,l\le 3}|w_{m,i}-w_{m,l}|\to 0}$
. This, along with property (iv), implies that
${\max _{1\le i,l\le 3}|w_{m,i}-w_{m,l}|\to 0}$
. This, along with property (iv), implies that
![]() $\gamma _{m-1,r_i}\subset B(w_{m,1}, 2\rho )$
,
$\gamma _{m-1,r_i}\subset B(w_{m,1}, 2\rho )$
,
![]() $i=1,2,3$
, for all big m. Since, for big m, differences of arguments of all
$i=1,2,3$
, for all big m. Since, for big m, differences of arguments of all
![]() $w_{m,i}$
are less than
$w_{m,i}$
are less than
![]() $\delta $
, and the same for
$\delta $
, and the same for
![]() $\tilde w_{m,i}$
, one can join all
$\tilde w_{m,i}$
, one can join all
![]() $w_{m,i}$
by an arc
$w_{m,i}$
by an arc
![]() $D^m$
of equipotential of level
$D^m$
of equipotential of level
![]() $\tilde C_3$
and all
$\tilde C_3$
and all
![]() $\tilde w_{m,i}$
by an arc
$\tilde w_{m,i}$
by an arc
![]() $\tilde D^m$
of equipotential of the same level
$\tilde D^m$
of equipotential of the same level
![]() $\tilde C_3$
such that
$\tilde C_3$
such that
![]() $D^m,\tilde D^m\subset B(w_1,2\rho )$
. Let the end points of
$D^m,\tilde D^m\subset B(w_1,2\rho )$
. Let the end points of
![]() $D^m$
be, say,
$D^m$
be, say,
![]() $w_{m,1}$
and
$w_{m,1}$
and
![]() $w_{m,3}$
, so that
$w_{m,3}$
, so that
![]() $w_{m,2}\in D^m$
is in between. Since all three curves
$w_{m,2}\in D^m$
is in between. Since all three curves
![]() $\Gamma _{m-1,r_i}$
,
$\Gamma _{m-1,r_i}$
,
![]() $i=1,2,3$
, are pairwise disjoint, the end points of
$i=1,2,3$
, are pairwise disjoint, the end points of
![]() $\tilde D^m$
then have to be
$\tilde D^m$
then have to be
![]() $\tilde w_{m,1}$
and
$\tilde w_{m,1}$
and
![]() $\tilde w_{m,3}$
, so that
$\tilde w_{m,3}$
, so that
![]() $\tilde w_{m,2}\in \tilde D^m$
is in between. Therefore, we get a ‘big’ quadrilateral
$\tilde w_{m,2}\in \tilde D^m$
is in between. Therefore, we get a ‘big’ quadrilateral
![]() $\Pi _m^0\subset B(w_{m,1}, 2\rho )$
bounded by
$\Pi _m^0\subset B(w_{m,1}, 2\rho )$
bounded by
![]() $D^m,\tilde D^m, \Gamma _{m,1}, \Gamma _{m,3}$
where
$D^m,\tilde D^m, \Gamma _{m,1}, \Gamma _{m,3}$
where
![]() $\Gamma _{m,i}:=\Gamma _{m-1,r_i}$
,
$\Gamma _{m,i}:=\Gamma _{m-1,r_i}$
,
![]() $i=1,2,3$
. The curve
$i=1,2,3$
. The curve
![]() $\Gamma _{m,2}$
splits
$\Gamma _{m,2}$
splits
![]() $\Pi _m^0$
into two ‘small’ quadrilaterals
$\Pi _m^0$
into two ‘small’ quadrilaterals
![]() $\Pi _m^1,\Pi _m^2$
with a common curve
$\Pi _m^1,\Pi _m^2$
with a common curve
![]() $\Gamma _{m,2}$
in their boundaries. Recall now that the curve
$\Gamma _{m,2}$
in their boundaries. Recall now that the curve
![]() $\Gamma _{m,2}$
comes with a small Julia set
$\Gamma _{m,2}$
comes with a small Julia set
![]() $I_{m,2}$
of level either
$I_{m,2}$
of level either
![]() $m-1$
or m, such that
$m-1$
or m, such that
![]() $I_{m,2}\cap \Gamma _{m,2}$
is a single point while
$I_{m,2}\cap \Gamma _{m,2}$
is a single point while
![]() $I_{m,2}$
is disjoint with
$I_{m,2}$
is disjoint with
![]() $\Gamma _{m,1}$
,
$\Gamma _{m,1}$
,
![]() $\Gamma _{m,3}$
. Therefore,
$\Gamma _{m,3}$
. Therefore,
![]() $I_{m,2}\subset \Pi _m^0\subset B(w_{m,1}, 2\rho )$
, a contradiction with Remark 5.1.
$I_{m,2}\subset \Pi _m^0\subset B(w_{m,1}, 2\rho )$
, a contradiction with Remark 5.1.
6. Proof of Corollaries 1.3 and 1.4
Corollary 1.3 follows directly from the following proposition
Proposition 6.1. Let f be an infinitely renormalizable quadratic polynomial. Then the following conditions are equivalent.
-
(1)
 $f: J_\infty \to J_\infty $
has no invariant probability measure with positive exponent.
$f: J_\infty \to J_\infty $
has no invariant probability measure with positive exponent. -
(2) For every neighborhood W of P and every
 $\alpha \in (0,1)$
there exist
$\alpha \in (0,1)$
there exist
 $m_0$
and
$m_0$
and
 $n_0$
such that, for each
$n_0$
such that, for each
 $m\ge m_0$
and
$m\ge m_0$
and
 $x\in \mathrm {orb}(J_n)$
with
$x\in \mathrm {orb}(J_n)$
with
 $n\ge n_0$
, Additionally,
$n\ge n_0$
, Additionally, $$ \begin{align*}\frac{\#\{i| 0\le i<m, f^i(x)\in W\}}{m}>\alpha.\end{align*} $$
$$ \begin{align*}\frac{\#\{i| 0\le i<m, f^i(x)\in W\}}{m}>\alpha.\end{align*} $$
 $f: P\to P$
has no invariant probability measure with positive exponent.
$f: P\to P$
has no invariant probability measure with positive exponent.
-
(3) Every invariant probability measure of
 $f: J_\infty \to J_\infty $
is, in fact, supported on P and has zero exponent.
$f: J_\infty \to J_\infty $
is, in fact, supported on P and has zero exponent. -
(4) For every invariant probability ergodic measure
 $\mu $
of f on the Julia set J of f, either
$\mu $
of f on the Julia set J of f, either
 $\operatorname {\mathrm {supp}}(\mu )\cap J_\infty =\emptyset $
and its Lyapunov exponent
$\operatorname {\mathrm {supp}}(\mu )\cap J_\infty =\emptyset $
and its Lyapunov exponent
 $\chi (\mu )>0$
, or
$\chi (\mu )>0$
, or
 $\operatorname {\mathrm {supp}}(\mu )\subset P$
and
$\operatorname {\mathrm {supp}}(\mu )\subset P$
and
 $\chi (\mu )=0$
.
$\chi (\mu )=0$
.
Proof. (1)
![]() $\Rightarrow $
(2). Assume the contrary. Let
$\Rightarrow $
(2). Assume the contrary. Let
![]() $E=\mathbb {C}\setminus W$
. Since W is a neighborhood of a compact set P, the Euclidean distance
$E=\mathbb {C}\setminus W$
. Since W is a neighborhood of a compact set P, the Euclidean distance
![]() $d(E, P)>0$
. By a standard normality argument, as all periodic points of f are repelling, there are
$d(E, P)>0$
. By a standard normality argument, as all periodic points of f are repelling, there are
![]() $\unicode{x3bb}>1$
and
$\unicode{x3bb}>1$
and
![]() $k_0>0$
such that
$k_0>0$
such that
![]() ${|(f^k)'(y)|>\unicode{x3bb} }$
whenever
${|(f^k)'(y)|>\unicode{x3bb} }$
whenever
![]() $y, f^k(y)\in E$
and
$y, f^k(y)\in E$
and
![]() $k\ge k_0$
. As (2) does not hold, find
$k\ge k_0$
. As (2) does not hold, find
![]() $\alpha \in (0,1)$
, a sequence
$\alpha \in (0,1)$
, a sequence
![]() $n_k\to \infty $
, points
$n_k\to \infty $
, points
![]() $x_k\in \mathrm {orb}(J_{n_k})$
and a sequence
$x_k\in \mathrm {orb}(J_{n_k})$
and a sequence
![]() $m_k\to \infty $
such that, for each k,
$m_k\to \infty $
such that, for each k,
 $$ \begin{align*}\frac{\#\{i: 0\le i<m_k, f^i(x_k)\in E\}}{m_k}\ge\beta:=1-\alpha.\end{align*} $$
$$ \begin{align*}\frac{\#\{i: 0\le i<m_k, f^i(x_k)\in E\}}{m_k}\ge\beta:=1-\alpha.\end{align*} $$
Fix a big k such that
![]() $\beta m_k>3k_0$
and consider the times
$\beta m_k>3k_0$
and consider the times
![]() $0\le i_1^k<i_2^k<\cdots i_{l_k}^k<m_k$
where
$0\le i_1^k<i_2^k<\cdots i_{l_k}^k<m_k$
where
![]() $l_k/m_k\ge \beta $
such that
$l_k/m_k\ge \beta $
such that
![]() $f^i(x_k)\in E$
. Let
$f^i(x_k)\in E$
. Let
![]() $z_k=f^{i_1^k}(x_k)$
so that
$z_k=f^{i_1^k}(x_k)$
so that
![]() $z_k\in E\cap \mathrm {orb}(J_n)$
. Therefore, by the choice of
$z_k\in E\cap \mathrm {orb}(J_n)$
. Therefore, by the choice of
![]() $\unicode{x3bb} $
and
$\unicode{x3bb} $
and
![]() $k_0$
,
$k_0$
,
![]() $|(f^{m_k-i_1^k})'(z_k)|\ge \tilde {\unicode{x3bb}} ^{m_k}\ge \tilde {\unicode{x3bb}} ^{m_k-i_1}$
where
$|(f^{m_k-i_1^k})'(z_k)|\ge \tilde {\unicode{x3bb}} ^{m_k}\ge \tilde {\unicode{x3bb}} ^{m_k-i_1}$
where
![]() $\tilde {\unicode{x3bb}} =\unicode{x3bb} ^{{\beta }/{2k_0}}>1$
. In this way we get a sequence of measures
$\tilde {\unicode{x3bb}} =\unicode{x3bb} ^{{\beta }/{2k_0}}>1$
. In this way we get a sequence of measures
![]() $\mu _k=({1}/{m_k-i_1^k})\sum _{i=0}^{m_k-i_1^k-1}\delta _{f^i(z_k)}$
such that the Lyapunov exponent of
$\mu _k=({1}/{m_k-i_1^k})\sum _{i=0}^{m_k-i_1^k-1}\delta _{f^i(z_k)}$
such that the Lyapunov exponent of
![]() $\mu _k$
is at least
$\mu _k$
is at least
![]() $\log \tilde {\unicode{x3bb}}>0$
. Passing to a subsequence, one can assume that
$\log \tilde {\unicode{x3bb}}>0$
. Passing to a subsequence, one can assume that
![]() $\{\mu _k\}$
converges weak-* to a measure
$\{\mu _k\}$
converges weak-* to a measure
![]() $\mu $
. Then
$\mu $
. Then
![]() $\mu $
is an f-invariant probability measure on
$\mu $
is an f-invariant probability measure on
![]() $J_\infty =\cap \mathrm {orb}(J_n)$
with the exponent at least
$J_\infty =\cap \mathrm {orb}(J_n)$
with the exponent at least
![]() $\log \tilde {\unicode{x3bb}}> 0$
, a contradiction with (1).
$\log \tilde {\unicode{x3bb}}> 0$
, a contradiction with (1).
(2)
![]() $\Rightarrow $
(3). By Birkhoff’s ergodic theorem along with [Reference Przytycki22].
$\Rightarrow $
(3). By Birkhoff’s ergodic theorem along with [Reference Przytycki22].
(3)
![]() $\Rightarrow $
(4). Let
$\Rightarrow $
(4). Let
![]() $\mu $
be as in (4) and
$\mu $
be as in (4) and
![]() $\overline {U}\cap P=\emptyset $
for some open set U with
$\overline {U}\cap P=\emptyset $
for some open set U with
![]() $\mu (U)>0$
. Let
$\mu (U)>0$
. Let
![]() $F:U\to U$
be the first return map equipped with the induced invariant measure
$F:U\to U$
be the first return map equipped with the induced invariant measure
![]() $\mu _U$
. By Birkhoff’s ergodic theorem and by an argument as in (1)
$\mu _U$
. By Birkhoff’s ergodic theorem and by an argument as in (1)
![]() $\Rightarrow $
(2), the exponent
$\Rightarrow $
(2), the exponent
![]() $\chi _F(\mu _U)$
of F with respect to
$\chi _F(\mu _U)$
of F with respect to
![]() $\mu _U$
is strictly positive. Hence,
$\mu _U$
is strictly positive. Hence,
![]() $\chi (\mu )=\mu (U)\chi _F(\mu _U)$
is positive too. This proves the implication.
$\chi (\mu )=\mu (U)\chi _F(\mu _U)$
is positive too. This proves the implication.
And (4) obviously implies (1).
Proof of Corollary 1.4
If
![]() $\overline \chi (x)$
were strictly positive, for some
$\overline \chi (x)$
were strictly positive, for some
![]() $x\in J_\infty $
, that would imply, by a standard argument (see the proof of Corollary 1.3), the existence of an f-invariant measure with positive exponent supported in
$x\in J_\infty $
, that would imply, by a standard argument (see the proof of Corollary 1.3), the existence of an f-invariant measure with positive exponent supported in
![]() $\omega (x)\subset J_\infty $
, with a contradiction to Theorem 1.1. This proves (1.1). By [Reference Levin, Przytycki and Shen13],
$\omega (x)\subset J_\infty $
, with a contradiction to Theorem 1.1. This proves (1.1). By [Reference Levin, Przytycki and Shen13],
![]() $\liminf _{n\to \infty } ({1}/{n})\log |(f^n)'(c)|\ge 0$
. On the other hand, by (1.1),
$\liminf _{n\to \infty } ({1}/{n})\log |(f^n)'(c)|\ge 0$
. On the other hand, by (1.1),
![]() $\overline \chi (c)\le 0$
, which proves (1.2).
$\overline \chi (c)\le 0$
, which proves (1.2).
Acknowledgements
The conclusion (1.2) of Corollary 1.4 that the Lyapunov exponent at the critical value equals zero partly answers a question by Weixiao Shen (Shen asked the following question, in relation to Corollary 5.5 of [Reference Levin, Przytycki and Shen13]: is it possible that the upper Lyapunov exponent at a critical value
![]() $v$
of a polynomial g is positive, assuming that g is infinitely renormalizable around
$v$
of a polynomial g is positive, assuming that g is infinitely renormalizable around
![]() $v$
? See also Remark 1.1). which inspired the present work as well as the previous paper [Reference Levin and Przytycki12]. The authors thank the referee for careful reading the paper and many helpful comments. The first author was partially supported by ISF grant 1226/17, Israel. The second author was partially supported by the National Science Centre, Poland, Grant OPUS 21 ‘Holomorphic dynamics, fractals, thermodynamic formalism’, 2021/41/B/ST1/00461.
$v$
? See also Remark 1.1). which inspired the present work as well as the previous paper [Reference Levin and Przytycki12]. The authors thank the referee for careful reading the paper and many helpful comments. The first author was partially supported by ISF grant 1226/17, Israel. The second author was partially supported by the National Science Centre, Poland, Grant OPUS 21 ‘Holomorphic dynamics, fractals, thermodynamic formalism’, 2021/41/B/ST1/00461.