Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2025-01-01T22:49:28.888Z Has data issue: false hasContentIssue false
  • English
  • Français

Rank-one non-singular actions of countable groups and their odometer factors

Part of: Ergodic theory

Published online by Cambridge University Press:  30 September 2024

ALEXANDRE I. DANILENKO Open the ORCID record for ALEXANDRE I. DANILENKO [Opens in a new window]  and
MYKYTA I. VIEPRIK
ALEXANDRE I. DANILENKO*
Affiliation:
B. Verkin Institute for Low Temperature Physics and Engineering of the National Academy of Sciences of Ukraine, 47 Nauky Ave., Kharkiv 61164, Ukraine e-mail: alexandre.danilenko@gmail.com Mathematical Institute of the Polish Academy of Sciences, ul. Śniadeckich 8, Warszawa 00-656, Poland
MYKYTA I. VIEPRIK
Affiliation:
Mathematical Institute of the Polish Academy of Sciences, ul. Śniadeckich 8, Warszawa 00-656, Poland V. N. Karazin Kharkiv National University, 4 Svobody sq., Kharkiv 61077, Ukraine (e-mail: nikita.veprik@gmail.com)
*
e-mail: alexandre.danilenko@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

For an arbitrary countable discrete infinite group G, non-singular rank-one actions are introduced. It is shown that the class of non-singular rank-one actions coincides with the class of non-singular 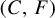$(C,F)$-actions. Given a decreasing sequence of cofinite subgroups in G with $\bigcap _{n=1}^\infty \bigcap _{g\in G}g\Gamma _ng^{-1}=\{1_G\}$, the projective limit of the homogeneous G-spaces 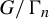$G/\Gamma _n$ as $n\to \infty $ is a G-space. Endowing this G-space with an ergodic non-singular non-atomic measure, we obtain a dynamical system which is called a non-singular odometer. Necessary and sufficient conditions are found for a rank-one non-singular G-action to have a finite factor and a non-singular odometer factor in terms of the underlying $(C,F)$-parameters. Similar conditions are also found for a rank-one non-singular G-action to be isomorphic to an odometer. Minimal Radon uniquely ergodic locally compact Cantor models are constructed for the non-singular rank-one extensions of odometers. Several concrete examples are constructed and several facts are proved that illustrate a sharp difference of the non-singular non-commutative case from the classical finite measure preserving one: odometer actions which are not of rank-one and factors of rank-one systems which are not of rank one; however, each probability preserving odometer is a factor of an infinite measure preserving rank-one system, etc.

Keywords

rank-one transformationodometerfactor

MSC classification

Primary: 37A40: Nonsingular (and infinite-measure preserving) transformations 37A15: General groups of measure-preserving transformations
Secondary: 37A35: Entropy and other invariants, isomorphism, classification
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , First View , pp. 1 - 51
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aaronson, J.. Infinite Ergodic Theory. American Mathematical Society, Providence, RI, 1997.Google Scholar
Adams, T., Friedman, N. and Silva, C. E.. Rank one power weakly mixing nonsingular transformations. Ergod. Th. & Dynam. Sys. 21 (2001), 1321–1332.CrossRefGoogle Scholar
Berendschot, T. and Vaes, S.. Bernoulli actions of type $\mathrm{II}{\mathrm{I}}_0$ with prescribed associated flow. Inst. Math. Jussieu 23 (2024), 71–122.CrossRefGoogle Scholar
Cortez, M. I. and Petite, S.. $\mathrm{G}$ -odometers and their almost one-to-one extensions. J. Lond. Math. Soc. (2) 78 (2008), 1–20.CrossRefGoogle Scholar
Connes, A. and Woods, E. J.. Approximately transitive flows and ITPFI factors. Ergod. Th. & Dynam. Sys. 5 (1985), 203–236.CrossRefGoogle Scholar
Danilenko, A. I.. Funny rank-one weak mixing for nonsingular abelian actions. Israel J. Math. 121 (2001), 29–54.CrossRefGoogle Scholar
Danilenko, A. I.. Infinite rank one actions and nonsingular Chacon transformations. Illinois J. Math. 48 (2004), 769–786.CrossRefGoogle Scholar
Danilenko, A. I.. Actions of finite rank: weak rational ergodicity and partial rigidity. Ergod. Th. & Dynam. Sys. 36 (2016), 2138–2171.CrossRefGoogle Scholar
Danilenko, A. I.. Rank-one actions, their (C,F)-models and constructions with bounded parameters. J. Anal. Math. 139 (2019), 697–749.CrossRefGoogle Scholar
Danilenko, A. I. and del Junco, A.. Almost continuous orbit equivalence for non-singular homeomorphisms. Israel J. Math. 183 (2011), 165–188.CrossRefGoogle Scholar
Danilenko, A. I. and Lemańczyk, M.. Odometer actions of the Heisenberg group. J. Anal. Math. 128 (2016), 107–157.CrossRefGoogle Scholar
Danilenko, A. I. and Silva, C. E.. Ergodic theory: nonsingular transformations. Ergodic Theory (Encyclopedia of Complexity and Systems Science Series). Ed. Meyers, R. A.. Springer, New York, NY, 2023, pp. 233–292.CrossRefGoogle Scholar
Danilenko, A. I. and Vieprik, M. I.. Explicit rank-1 constructions for irrational rotations. Studia Math. 270 (2023), 121–144.CrossRefGoogle Scholar
del Junco, A.. Transformations with discrete spectrum are stacking transformations. Canad. J. Math. 28 (1976), 836–839.CrossRefGoogle Scholar
del Junco, A.. A simple map with no prime factors. Israel J. Math. 104 (1998), 301–320.CrossRefGoogle Scholar
del Junco, A., Rahe, M. and Swanson, L.. Chacon’s automorphism has minimal self-joinings. J. Anal. Math. 37 (1980), 276–284.CrossRefGoogle Scholar
del Junco, A. and Rudolph, D.. On ergodic actions whose self-joinings are graphs. Ergod. Th. & Dynam. Sys. 7 (1987), 531–557.CrossRefGoogle Scholar
Dooley, A. H. and Hamachi, T.. Markov odometer actions not of product type. Ergod. Th. & Dynam. Sys. 23 (2003), 813–829.CrossRefGoogle Scholar
Effros, E. G.. Transformation groups and ${\mathrm{C}}^{\ast }$ -algebras. Ann. of Math. (2) 81 (1965), 38–55.CrossRefGoogle Scholar
Ferenczi, S.. Systems of finite rank. Colloq. Math. 73 (1997), 35–65.CrossRefGoogle Scholar
Foreman, M., Gao, S., Hill, A., Silva, C. E. and Weiss, B.. Rank-one transformations, odometers, and finite factors. Israel J. Math. 255 (2023), 231–249.CrossRefGoogle Scholar
Grigorchuk, R. I.. On Burnside’s problem on periodic groups. Russian Funktsional. Anal. i Prilozhen. 14 (1980), 53–54.Google Scholar
Greschonig, G. and Schmidt, K.. Ergodic decomposition of quasi-invariant probability measures. Colloq. Math. 84/85 (2000), 495–514.CrossRefGoogle Scholar
Hamachi, T.. A measure theoretical proof of the Connes–Woods theorem on AT-flows. Pacific J. Math. 154 (1992), 67–85.CrossRefGoogle Scholar
Hamachi, T. and Silva, C. E.. On nonsingular Chacon transformations. Illinois J. Math. 44 (2000), 868–883.CrossRefGoogle Scholar
Hewitt, E. and Ross, K. A.. Abstract Harmonic Analysis: Volume I. Springer, Berlin, 1963.Google Scholar
Johnson, A. S. A. and McClendon, D. M.. Finite odometer factors of rank one group actions. Indag. Math. (N.S.). doi:10.1016/j.indag.2024.04.012. Published online 4 May 2024.CrossRefGoogle Scholar
Lightwood, S., Şahin, A. and Ugarcovici, I.. The structure and the spectrum of Heisenberg odometers. Proc. Amer. Math. Soc. 142 (2014), 2429–2443.CrossRefGoogle Scholar
Rudolph, D. J.. An example of a measure preserving map with minimal self-joinings, and applications. J. Anal. Math. 35 (1979), 97–122.CrossRefGoogle Scholar
Rudolph, D. J. and Silva, C.E.. Minimal self-joinings for nonsingular transformations. Ergod. Th. & Dynam. Sys. 9 (1989), 759–800.CrossRefGoogle Scholar
Yuasa, H.. Uniform sets for infinite measure-preserving systems. J. Anal. Math. 120 (2013), 333–356.CrossRefGoogle Scholar