Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T14:36:48.712Z Has data issue: false hasContentIssue false
  • English
  • Français

A relaxation result for energies defined on pairs set-function and applications

Published online by Cambridge University Press:  20 July 2007

Andrea Braides ,
Antonin Chambolle  and
Margherita Solci
Andrea Braides
Affiliation:
Dip. di Matematica, Università di Roma “Tor Vergata”, via della Ricerca Scientifica, 00133 Roma, Italy.
Antonin Chambolle
Affiliation:
CMAP, École Polytechnique, CNRS, 91128 Palaiseau, France; antonin.chambolle@polytechnique.fr
Margherita Solci
Affiliation:
DAP, Università di Sassari, Palazzo Pou Salit, 07041 Alghero, Italy.
Get access

Abstract


We consider, in an open subset Ω of ${\mathbb R}^N$ 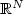, energies depending on the perimeter of a subset $E\subset\Omega$ 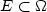(or some equivalent surface integral) and on a function u which isdefined only on $\Omega\setminus E$ 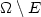. We compute the lower semicontinuous envelopeof such energies. This relaxation has to take intoaccount the fact that in the limit, the “holes” E maycollapse into a discontinuity of u, whose surface will be countedtwice in the relaxed energy. We discuss some situations where suchenergies appear, and give, as an application, a new proofof convergence for an extensionof Ambrosio-Tortorelli's approximation to the Mumford-Shah functional.


Keywords

Relaxationfree discontinuity problemsΓ-convergence
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 13 , Issue 4 , October 2007 , pp. 717 - 734
Copyright
© EDP Sciences, SMAI, 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alberti, G. and DeSimone, A., Wetting of rough surfaces: a homogenization approach. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 461 (2005) 79–97. CrossRef
Ambrosio, L. and Braides, A., Functionals defined on partitions of sets of finite perimeter, I: integral representation and Γ-convergence. J. Math. Pures. Appl. 69 (1990) 285–305.
Ambrosio, L. and Braides, A., Functionals defined on partitions of sets of finite perimeter, II: semicontinuity, relaxation and homogenization. J. Math. Pures. Appl. 69 (1990) 307–333.
Ambrosio, L. and Tortorelli, V.M., Approximation of functionals depending on jumps by elliptic functionals via Γ-convergence. Comm. Pure Appl. Math. 43 (1990) 999–1036. CrossRef
L. Ambrosio, N. Fusco and D. Pallara, Functions of Bounded Variation and Free Discontinuity Problems. Oxford University Press, Oxford (2000).
Bellettini, G., Paolini, M. and Venturini, S., Some results on surface measures in calculus of variations. Ann. Mat. Pura Appl. 170 (1996) 329–357.
Bonnetier, E. and Chambolle, A., Computing the equilibrium configuration of epitaxially strained crystalline films. SIAM J. Appl. Math. 62 (2002) 1093–1121.
G. Bouchitté and P. Seppecher, Cahn and Hilliard fluid on an oscillating boundary. Motion by mean curvature and related topics (Trento, 1992), de Gruyter, Berlin (1994) 23–42.
Bouchitté, G., Braides, A. and Buttazzo, G., Relaxation results for some free discontinuity problems. J. Reine Angew. Math. 458 (1995) 1–18.
Bourdin, B. and Chambolle, A., Implementation of an adaptive finite-element approximation of the Mumford-Shah functional. Numer. Math. 85 (2000) 609–646. CrossRef
A. Braides, Approximation of Free-Discontinuity Problems. Lect. Notes Math. 1694, Springer, Berlin (1998).
A. Braides, Γ -convergence for Beginners. Oxford University Press, Oxford (2002).
A. Braides, A handbook of Γ>-convergence, in Handbook of Differential Equations. Stationary Partial Differential Equations, Vol. 3, M. Chipot and P. Quittner Eds., Elsevier (2006).
A. Braides and V. Chiadò Piat, Integral representation results for functionals defined in $SBV(\Omega;{\rm I\! R^m})$ . J. Math. Pures Appl. 75 (1996) 595–626.
Braides, A. and March, R., Approximation by Γ-convergence of a curvature-depending functional in Visual Reconstruction. Comm. Pure Appl. Math. 58 (2006) 71–121. CrossRef
A. Braides and M. Solci, A remark on the approximation of free-discontinuity problems. Manuscript (2003).
Braides, A., Defranceschi, A. and Vitali, E., Homogenization of free discontinuity problems. Arch. Rational Mech. Anal. 135 (1996) 297–356. CrossRef
Buffoni, B., Existence and conditional energetic stability of capillary-gravity solitary water waves by minimisation. Arch. Ration. Mech. Anal. 173 (2004) 25–68. CrossRef
Chambolle, A. and Solci, M., Interaction of a bulk and a surface energy with a geometrical constraint. SIAM J. Math. Anal. 39 (2007) 77–102. CrossRef
A. Chambolle, E. Séré and C.Zanini, Progressive water-waves: a global variational approach. (In preparation).
E. Giusti, Minimal surfaces and functions of bounded variation. Birkhäuser Verlag, Basel (1984).
J.M. Morel and S. Solimini, Variational Methods in Image Segmentation. Progr. Nonlinear Differ. Equ. Appl. 14, Birkhäuser, Basel (1995).
Mumford, D. and Shah, J., Optimal approximations by piecewise smooth functions and associated variational problems. Comm. Pure Appl. Math. 42 (1989) 577–685. CrossRef