Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-23T03:57:37.757Z Has data issue: false hasContentIssue false
  • English
  • Français

Graph selectors and viscosity solutions on Lagrangian manifolds

Published online by Cambridge University Press:  11 October 2006

David McCaffrey
David McCaffrey*
Affiliation:
University of Sheffield, Dept. of Automatic Control and Systems Engineering, Mappin Street, Sheffield, S1 3JD, UK; david@mccaffrey275.fsnet.co.uk
Get access

Abstract

Let $\Lambda $ 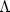be a Lagrangian submanifold of $T^{*}X$ 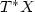for some closedmanifold X. Let $S(x,\xi )$ 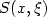be a generating function for $\Lambda $ 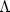whichis quadratic at infinity, and let W(x) be the corresponding graph selectorfor $\Lambda ,$ 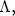in the sense of Chaperon-Sikorav-Viterbo, so that thereexists a subset $X_{0}\subset X$ 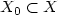of measure zero such that W is Lipschitzcontinuous on X, smooth on $X\backslash X_{0}$ 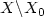and $(x,\partial W/\partialx(x))\in \Lambda $ 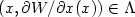for $X\backslash X_{0}.$ 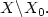Let H(x,p)=0 for $(x,p)\in\Lambda$ 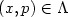. Then W is a classical solution to $H(x,\partial W/\partialx(x))=0$ 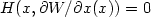on $X\backslash X_{0}$ 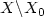and extends to a Lipschitz function on thewhole of X. Viterbo refers to W as a variational solution. We prove that W is also a viscosity solution under some simple and natural conditions.We also prove that these conditions are satisfied in many cases, includingcertain commonly occuring cases where H(x,p) is not convex in p.

Keywords

Viscosity solutionLagrangian manifoldgraph selector.
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 12 , Issue 4 , October 2006 , pp. 795 - 815
Copyright
© EDP Sciences, SMAI, 2006

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bardi, M. and Evans, L.C., Hopf's, On formula for solutions of Hamilton-Jacobi equations. Nonlinear Anal. Th. Meth. Appl. 8 (1984) 1373–1381. CrossRef
Cardin, F., On viscosity solutions and geometrical solutions of Hamilton-Jacobi equations. Nonlinear Anal. Th. Meth. Appl. 20 (1993) 713–719. CrossRef
M. Chaperon, Lois de conservation et geometrie symplectique. C.R. Acad. Sci. Paris Ser. I Math., 312 (1991) 345–348.
F.H. Clarke, Optimization and Nonsmooth Analysis. J. Wiley, New York (1983).
Crandall, M.G. and Lions, P.L., Viscosity solutions of Hamilton-Jacobi equations. Trans. AMS 277 (1983) 1–42. CrossRef
Crandall, M.G., Evans, L.C. and Lions, P.L., Some properties of viscosity solutions of Hamilton-Jacobi equations. Trans. AMS 282 (1984) 487–502. CrossRef
M.V. Day, On Lagrange manifolds and viscosity solutions. J. Math. Syst. Estim. Contr. 8 (1998) http://www.math.vt.edu/people/day/research/LMVS.pdf
S.Yu. Dobrokhotov, V.N. Kolokoltsov and V.P. Maslov, Quantization of the Bellman equation, exponential asymptotics and tunneling, in Advances in Soviet Mathematics, V.P. Maslov and S.N. Samborskii, Eds., American Mathematical Society, Providence, Rhode Island 13 (1992) 1–46 .
W.H Fleming and H.M. Soner, Controlled markov processes and viscosity solutions. Springer-Verlag, New York (1993).
Frankowska, H., Hamilton-Jacobi equations: viscosity solutions and generalised gradients. J. Math. Anal. Appl. 141 (1989) 21–26. CrossRef
Hopf, E., Generalized solutions of non-linear equations of first order. J. Math. Mech. 14 (1965) 951–973.
T. Joukovskaia, Thèse de Doctorat, Université de Paris VII, Denis Diderot (1993).
Laudenbach, F. and Sikorav, J.C., Persistance d'intersection avec la section nulle au cours d'une isotopie hamiltonienne dans un fibre cotangent. Invent. Math. 82 (1985) 349–357. CrossRef
J. Mawhin and M. Willem, Critical Point Theory and Hamiltonian Systems. Applied Mathematical Sciences Series 74, Springer-Verlag, Berlin (1989).
McCaffrey, D. and Banks, S.P., Lagrangian Manifolds, Viscosity Solutions and Maslov Index. J. Convex Anal. 9 (2002) 185–224.
D. McCaffrey, Viscosity Solutions on Lagrangian Manifolds and Connections with Tunnelling Operators, in Idempotent Mathematics and Mathematical Physics, V.P. Maslov and G.L. Litvinov Eds., Contemp. Math. 377, American Mathematical Society, Providence, Rhode Island (2005).
D. McCaffrey, Geometric existence theory for the control-affine $H_{\infty}$ problem, to appear in J. Math. Anal & Appl. (August 2005).
Paternain, G.P., Polterovich, L. and Siburg, K.F., Boundary rigidity for Lagrangian submanifolds, non-removable intersections and Aubry-Mather theory. Moscow Math. J. 3 (2003) 593–619.
J.C. Sikorav, Sur les immersions lagrangiennes dans un fibre cotangent admettant une phase generatrice globale. C. R. Acad. Sci. Paris, Ser. I Math. 302 (1986) 119–122.
Soravia, P., $H_{\infty }$ control of nonlinear systems: differential games and viscosity solutions. SIAM J. Contr. Opt. 34 (1996) 1071–1097. CrossRef
van der Schaft, A.J., On a state space approach to nonlinear $H_{\infty }$ control. Syst. Contr. Lett. 16 (1991) 1–8. CrossRef
A.J. van der Schaft, L 2 gain analysis of nonlinear systems and nonlinear state feedback $H_{\infty}$ control. IEEE Trans. Automatic Control AC-37 (1992) 770–784.
Viterbo, C., Symplectic topology as the geometry of generating functions. Math. Ann. 292 (1992) 685–710. CrossRef
C. Viterbo, Solutions d'equations d'Hamilton-Jacobi et geometrie symplectique, Addendum to: Séminaire sur les équations aux Dérivés Partielles 1994–1995, École Polytech., Palaiseau (1996).
A. Ottolengi and C. Viterbo, Solutions généralisées pour l'équation de Hamilton-Jacobi dans le cas d'évolution, unpublished.
A. Weinstein, Lectures on symplectic manifolds, Regional Conference Series in Mathematics 29, Conference Board of the Mathematical Sciences, AMS, Providence, Rhode Island (1977).