Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T23:13:02.475Z Has data issue: false hasContentIssue false
  • English
  • Français

Adaptive density estimation under weak dependence

Published online by Cambridge University Press:  10 May 2010

Irène Gannaz  and
Olivier Wintenberger
Irène Gannaz
Affiliation:
Laboratoire Jean Kuntzmann, INP Grenoble, 38041 Grenoble Cedex 9, France
Olivier Wintenberger
Affiliation:
SAMOS-MATISSE (Statistique Appliquée et Modélisation Stochastique), Centre d'Économie de la Sorbonne Université Paris 1 – Panthéon-Sorbonne, CNRS 90, Rue de Tolbiac, 75634 Paris Cedex 13, France
Get access

Abstract

Assume that (Xt )t∈Z is a real valued time seriesadmitting a common marginal density f with respect to Lebesgue's measure. [Donoho et al. Ann. Stat.24 (1996) 508–539] propose near-minimax estimators $\widehat f_n$ 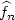based on thresholding wavelets to estimate f on a compact set in an independent and identically distributed setting. The aim of the present work is to extend these results to general weak dependent contexts. Weak dependence assumptions are expressed as decreasing bounds of covariance terms and are detailed for different examples. The threshold levels in estimators $\widehat f_n$ 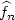depend on weak dependence properties of the sequence (Xt )t∈Z through the constant. If these properties are unknown, we propose cross-validation procedures to get new estimators. These procedures are illustrated via simulations of dynamical systems and non causal infinite moving averages. We also discuss the efficiency of our estimators with respect to the decrease of covariances bounds.

Keywords

Adaptive estimationcross validationhard thresholdingnear minimax resultsnonparametric density estimationsoft thresholdingwaveletsweak dependence
Type
Research Article
Information
ESAIM: Probability and Statistics , Volume 14 , 2010 , pp. 151 - 172
Copyright
© EDP Sciences, SMAI, 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andrews, D., Non strong mixing autoregressive processes. J. Appl. Probab. 21 (1984) 930–934. CrossRef
Bosq, D. and Guegan, D., Nonparametric estimation of the chaotic function and the invariant measure of a dynamical system. Stat. Probab. Lett. 25 (1995) 201–212. CrossRef
Comte, F. and Merlevède, F., Adaptive estimation of the stationary density of discrete and continuous time mixing processes. ESAIM: PS 6 (2002) 211–238. CrossRef
I. Daubechies, Ten Lectures on Wavelets, volume 61. SIAM Press (1992).
Dedecker, J. and Prieur, C., New dependence coefficients: Examples and applications to statistics. Probab. Theory Relat. Fields 132 (2005) 203–235. CrossRef
Dedecker, J. and Prieur, C., An empirical central limit theorem for dependent sequences. Stoch. Process. Appl. 117 (2007) 121–142. CrossRef
J. Dedecker, P. Doukhan, G. Lang, J.R. Leon, S. Louhichi and C. Prieur, Weak Dependence: Models, Theory and Applications. Springer-Verlag (2007).
Donoho, D., Johnstone, I., Kerkyacharian, G. and Picard, D., Density estimation by wavelet thresholding. Ann. Stat. 24 (1996) 508–539.
Doukhan, P. and Louhichi, S., A new weak dependence condition and applications to moment inequalities. Stoch. Process. Appl. 84 (1999) 313–342. CrossRef
Doukhan, P. and Neumann, M., Bernstein, A type inequality for times series. Stoch. Process. Appl. 117 (2007) 878–903. CrossRef
P. Doukhan, G. Teyssière and P. Winant, Vector valued ARCH infinity processes, in Dependence in Probability and Statistics . Lect. Notes Statist. Springer, New York (2006).
Doukhan, P. and Truquet, L., A fixed point approach to model random fields. Alea 2 (2007) 111–132.
Doukhan, P. and Wintenberger, O., Weakly dependent chains with infinite memory. Stoch. Process. Appl. 118 (2008) 1997–2013. CrossRef
Doukhan, P. and Wintenberger, O., Invariance principle for new weakly dependent stationary models. Probab. Math. Statist. 27 (2007) 45–73.
Gouëzel, S., Central limit theorem and stable laws for intermittent maps. Probab. Theory Relat. Fields 128 (2004) 82–122. CrossRef
W. Hardle, G. Kerkyacharian, D. Picard and A. Tsybakov, Wavelets Approximation and Statistical Applications. Lect. Notes Statist. 129. Springer-Verlag (1998).
A. Juditsky and S. Lambert-Lacroix, On minimax density estimation on $\mathbb{R}$ . Bernoulli, 10 (2004) 187–220.
Liverani, C., Saussol, B. and Vaienti, S., A probabilistic approach to intermittency. Ergodic Theory Dynam. Syst. 19 (1999) 671–686. CrossRef
Mallat, S., A theory for multiresolution signal decomposition: the wavelet representation. IEEE Trans. Pattern Anal. Machine Intelligence 11 (1989) 674–693. CrossRef
V. Maume-Deschamps, Exponential inequalities and functional estimations for weak dependent data; applications to dynamical systems. Stoch. Dynam. 6 (2006) 535–560.
Y. Meyer, Wavelets and Operators. Cambridge University Press (1992).
C. Prieur, Applications statistiques de suites faiblement dépendantes et de systèmes dynamiques. Ph.D. thesis, CREST, 2001.
N. Ragache and O. Wintenberger, Convergence rates for density estimators of weakly dependent time series, in Dependence in Probability and Statistics , P. Bertail, P. Doukhan, and P. Soulier (Eds.). Lect. Notes Statist. 187. Springer, New York (2006), pp. 349–372.
K. Tribouley and G. Viennet, $\mbox{L}_p$ -adaptive density estimation in a β-mixing framework. Ann. Inst. H. Poincaré, B 34 (1998) 179–208.
Vanharen, M.-L., Estimation par ondelettes dans les systèmes dynamiques. C. R. Acad. Sci. Paris 342 (2006) 523–525. CrossRef
M. Vannucci, Nonparametric density estimation using wavelets. Tech. Rep., Texas A and M University, 1998.
M. Viana, Stochastic dynamics of deterministic systems. Available at http://w3.impa.br/~viana (1997).
B. Vidakovic, Pollen bases and Daubechies-Lagarias algorithm in MATLAB (2002). Available at http://www2.isye.gatech.edu/~brani/datasoft/DL.pdf.
Wavelab. http://www-stat.stanford.edu/~wavelab/.
Young, L., Recurrence times and rates of mixing. Isr. J. Math. 110 (1999) 0021–2172. CrossRef