No CrossRef data available.
Article contents
Estimation of the hazard function in a semiparametric model with covariate measurement error
Published online by Cambridge University Press: 26 March 2009
Abstract
We consider a failure hazard function,conditional on a time-independent covariate Z,given by $\eta_{\gamma^0}(t)f_{\beta^0}(Z)$ 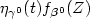 . The baseline hazardfunction $\eta_{\gamma^0}$
. The baseline hazardfunction $\eta_{\gamma^0}$ 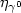 and the relative risk $f_{\beta^0}$
and the relative risk $f_{\beta^0}$ 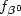 both belong to parametricfamilies with $\theta^0=(\beta^0,\gamma^0)^\top\in \mathbb{R}^{m+p}$
both belong to parametricfamilies with $\theta^0=(\beta^0,\gamma^0)^\top\in \mathbb{R}^{m+p}$ 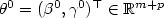 . The covariate Z has an unknown density and is measured with an error through anadditive error model U = Z + ε where ε is a random variable, independent from Z, withknown density $f_\varepsilon$
. The covariate Z has an unknown density and is measured with an error through anadditive error model U = Z + ε where ε is a random variable, independent from Z, withknown density $f_\varepsilon$ 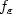 .We observe a n-sample (Xi, Di, Ui), i = 1, ..., n, where X i isthe minimum between the failure time and the censoring time,and D i is the censoring indicator.Using least square criterion and deconvolution methods, we propose a consistent estimator of θ 0 using the observationsn-sample (Xi, Di, Ui), i = 1, ..., n.
We give an upper bound for its riskwhich depends on the smoothness properties of $f_\varepsilon$
.We observe a n-sample (Xi, Di, Ui), i = 1, ..., n, where X i isthe minimum between the failure time and the censoring time,and D i is the censoring indicator.Using least square criterion and deconvolution methods, we propose a consistent estimator of θ 0 using the observationsn-sample (Xi, Di, Ui), i = 1, ..., n.
We give an upper bound for its riskwhich depends on the smoothness properties of $f_\varepsilon$ 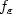 and $f_\beta(z)$
and $f_\beta(z)$ 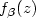 as afunction of z, and we derive sufficient conditionsfor the $\sqrt{n}$
as afunction of z, and we derive sufficient conditionsfor the $\sqrt{n}$ 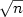 -consistency.We give detailed examples consideringvarious type of relative risks $f_{\beta}$
-consistency.We give detailed examples consideringvarious type of relative risks $f_{\beta}$ 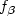 and various types of errordensity $f_\varepsilon$
and various types of errordensity $f_\varepsilon$ 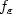 . In particular, in the Cox model and inthe excess risk model, the estimator of θ 0 is $\sqrt{n}$
. In particular, in the Cox model and inthe excess risk model, the estimator of θ 0 is $\sqrt{n}$ 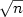 -consistent and asymptotically Gaussianregardless of the form of $f_\varepsilon$
-consistent and asymptotically Gaussianregardless of the form of $f_\varepsilon$ 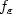 .
.
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- © EDP Sciences, SMAI, 2009

