Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-19T08:15:42.720Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotics of the principal eigenvalue of the Laplacian in 2D periodic domains with small traps

Part of: Partial differential equations Spectral theory and eigenvalue problems Representations of solutions

Published online by Cambridge University Press:  04 June 2021

F. PAQUIN-LEFEBVRE ,
S. IYANIWURA  and
M.J WARD Open the ORCID record for M.J WARD [Opens in a new window]
F. PAQUIN-LEFEBVRE
Affiliation:
Department of Mathematics, UBC, Vancouver, Canada emails: paquinl@math.ubc.ca; iyaniwura@math.ubc.ca; ward@math.ubc.ca
S. IYANIWURA
Affiliation:
Department of Mathematics, UBC, Vancouver, Canada emails: paquinl@math.ubc.ca; iyaniwura@math.ubc.ca; ward@math.ubc.ca
M.J WARD
Affiliation:
Department of Mathematics, UBC, Vancouver, Canada emails: paquinl@math.ubc.ca; iyaniwura@math.ubc.ca; ward@math.ubc.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

We derive and numerically implement various asymptotic approximations for the lowest or principal eigenvalue of the Laplacian with a periodic arrangement of localised traps of small 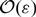\[\mathcal{O}(\varepsilon )\] spatial extent that are centred at the lattice points of an arbitrary Bravais lattice in 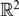\[{\mathbb{R}^2}\]. The expansion of this principal eigenvalue proceeds in powers of 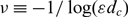\[\nu \equiv - 1/\log (\varepsilon {d_c})\], where dc is the logarithmic capacitance of the trap set. An explicit three-term approximation for this principal eigenvalue is derived using strong localised perturbation theory, with the coefficients in this series evaluated numerically by using an explicit formula for the source-neutral periodic Green’s function and its regular part. Moreover, a transcendental equation for an improved approximation to the principal eigenvalue, which effectively sums all the logarithmic terms in powers of v, is derived in terms of the regular part of the periodic Helmholtz Green’s function. By using an Ewald summation technique to first obtain a rapidly converging infinite series representation for this regular part, a simple Newton iteration scheme on the transcendental equation is implemented to numerically evaluate the improved ‘log-summed’ approximation to the principal eigenvalue. From a numerical computation of the PDE eigenvalue problem defined on the fundamental Wigner–Seitz (WS) cell for the lattice, it is shown that the three-term asymptotic approximation for the principal eigenvalue agrees well with the numerical result only for a rather small trap radius. In contrast, the log-summed asymptotic result provides a very close approximation to the principal eigenvalue even when the trap radius is only moderately small. For a circular trap, the first few transcendental correction terms that further improves the log-summed approximation for the principal eigenvalue are derived. Finally, it is shown numerically that, amongst all Bravais lattices with a fixed area of the primitive cell, the principal eigenvalue is maximised for a regular hexagonal arrangement of traps.

Keywords

EigenvalueBravais latticelogarithmic capacitanceperiodic Green’s functiontrap cluster

MSC classification

Primary: 35B25: Singular perturbations 35C20: Asymptotic expansions
Secondary: 35P15: Estimation of eigenvalues, upper and lower bounds
Type
Papers
Information
European Journal of Applied Mathematics , Volume 33 , Issue 4 , August 2022 , pp. 646 - 673
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aguarles, M. & de Haro, J. (2012) Derivation of the maximum voltage drop in power grids of integrated circuits with an array bonding package. Europ. J. Appl. Math. 23(6), 787–819.Google Scholar
Beylkin, G., Kurcz, C. & Monzón, L. (2008) Fast algorithms for Helmholtz Green’s functions. Proc. R. Soc. A 464, 3301–3326.Google Scholar
Bressloff, P. C. (2020) Asymptotic analysis of extended two-dimensional narrow capture problems, Submitted to Proc. Roy. Soc. A.CrossRefGoogle Scholar
Carroll, T. & Ortega-Cerdà, J. (2014) The maximum voltage drop in an on-chip power distribution network: Analysis of square, triangular, and hexagonal power pad arrangements. Europ. J. Appl. Math. 25(5), 531–551.CrossRefGoogle Scholar
Chapman, S. J., Hewett, D. P. & Trefethen, L. N. (2015) Mathematics of the Faraday cage. SIAM Rev. 57(3), 398–417.CrossRefGoogle Scholar
Chen, X. & Oshita, Y. (2007) An application of the modular function in nonlocal variational problems. Arch. Rat. Mech. Anal. 186(1), 109–132.CrossRefGoogle Scholar
Coker, D. A. & Torquato, S. (1995) Simulation of diffusion and trapping in digitized heterogeneous media. J. Appl. Phys. 77, 955.CrossRefGoogle Scholar
Dijkstra, W. & Hochstenbach, M. E. (2008) Numerical Approximation of the Logarithmic Capacity, CASA Report 08-09, Technical U. Eindhoven.Google Scholar
FlexPDE (2015) PDE Solutions Inc. http://www.pdesolutions.com Google Scholar
Grebenkov, D. (2019) Spectral theory of imperfect diffusion-controlled reactions on heterogeneous catalytic surfaces. J. Chem. Phys. 151, 104108.CrossRefGoogle ScholarPubMed
Hinch, J. (1991) Perturbation Methods . Cambridge Texts in Applied Mathematics. Cambridge University Press, Cambridge, U.K.Google Scholar
Iron, D., Rumsey, J., Ward, M. J. & Wei, J. C. (2014) Logarithmic expansions and the stability of periodic patterns of localized spots for reaction-diffusion systems in \[{\mathbb{R}^2}\]. J. Nonlin. Sci. 24(5), 564–627.CrossRefGoogle Scholar
Iyaniwura, S., Gou, J. & Ward, M. J. (2021) Synchronous oscillations for a coupled cell-bulk ODE-PDE model with localized cells on \[{\mathbb{R}^2}\], J. Eng. Math., 24 pages (to appear).CrossRefGoogle Scholar
Iyaniwura, S. & Ward, M. J. (2021) Asymptotic analysis for the mean first passage time in finite or spatially periodic 2-D domains with a cluster of small traps. ANZIAM J., 25 pages (to appear).CrossRefGoogle Scholar
Iyaniwura, S., Wong, T., MacDonald, C. B. & Ward, M. J. (2020) Optimization of the mean first passage time in near-disk and elliptical domains in 2-D with small absorbing traps. Submitted to SIAM Rev.CrossRefGoogle Scholar
Kansal, A. R. & Torquato, S. (2002) Prediction of trapping rates in mixtures of partially absorbing spheres. J. Chem. Phys. 116(24).CrossRefGoogle Scholar
Kolokolnikov, T., Titcombe, M. S. & Ward, M. J. (2005) Optimizing the fundamental Neumann eigenvalue for the Laplacian in a domain with small traps. Eur. J. Appl. Math. 16(2), 161–200.CrossRefGoogle Scholar
Kropinski, M. C., Lindsay, A. & Ward, M. J. (2011) Asymptotic analysis of localized solutions to some linear and nonlinear biharmonic eigenvalue problems. Stud. Appl. Math. 126(4), 397–408.CrossRefGoogle Scholar
Kurella, V., Tzou, J. C., Coombs, D. & Ward, M. J. (2015) Asymptotic analysis of first passage time problems inspired by ecology. Bull. Math. Biol. 77(1), 83–125.CrossRefGoogle Scholar
Lindsay, A., Kolokolnikov, T. & Ward, M. J. (2015) The transition to point constraint in a mixed biharmonic eigenvalue problem. SIAM J. Appl. Math. 75(3), 1193–1224.CrossRefGoogle Scholar
Lindsay, A. E., Tzou, J. C. & Kolokolnikov, T. (2015) Narrow escape problem with mixed trap and the effect of orientation. Phys. Rev. E. 91(3), 032111.CrossRefGoogle ScholarPubMed
The Mathworks, Inc., Natick, Massachusetts. (2018) MATLAB version 9.4.0.813654 (R2018a).Google Scholar
Olver, F. W. J., Daalhuis, A. B. O., Lozier, D. W., Schneider, B. I., Boisvert, R. F., Clark, C. W., Miller, B. R., Saunders, B. V., Cohl, H. S. & McClain, M. A. (Eds.) (2012). NIST Digital Library of Mathematical Functions. Release 1.0.26 of 2020-03-15. http://dlmf.nist.gov/ Google Scholar
Ozawa, S. (1981) Singular variation of domains and eigenvalues of the Laplacian. Duke Math. J. 48(4), 767–778.CrossRefGoogle Scholar
Piessens, R. (2018) The Hankel transform. In: Poularikas, A. D. (editor), Transforms and Applications Handbook, 3rd ed., Chapter 9. CRC Press, Boca Raton, Florida.Google Scholar
Pillay, S., Ward, M. J., Peirce, A. & Kolokolnikov, T. (2010) An asymptotic analysis of the mean first passage time for narrow escape problems: Part I: Two-dimensional domains. SIAM J. Multiscale Model. Simul. 8(3), 803–835.CrossRefGoogle Scholar
Ransford, T. (1995) Potential Theory in the Complex Plane. London Math. Soc. Stud. Texts 28. Cambridge University Press, Cambridge, U.K.CrossRefGoogle Scholar
Sanchez Hubert, J. & Sanchez Palencia, E. (1989) Vibration and Coupling of Continuous Systems. Springer, Berlin, Heidelberg.CrossRefGoogle Scholar
Schnitzer, O. & Craster, R. V. (2017) Bloch waves in an arbitrary two-dimensional lattice of subwavelength Dirichlet scatterers. SIAM J. Appl. Math. 77(6), 2119–2135.CrossRefGoogle Scholar
Torney, D. C. & Goldstein, B. (1987) Rates of diffusion-limited reaction in periodic systems. J. Stat. Phys. 49, 725–750.CrossRefGoogle Scholar
Trefethon, N. (2018) Series solution of Laplace problems. ANZIAM J. 60, 1–26.Google Scholar
Tzou, J. C. & Kolokolnikov, T. (2015) Mean first passage time for a small rotating trap inside a reflective disk. SIAM J. Multiscale Model. Simul. 13(1), 231–255.CrossRefGoogle Scholar
Ward, M. J. (2018) Spots, traps, and patches: Asymptotic analysis of localized solutions to some linear and nonlinear diffusive systems. Nonlinearity 31(8), R189.CrossRefGoogle Scholar
Ward, M. J., Henshaw, W. D. & Keller, J. B. (1993) Summing logarithmic expansions for singularly perturbed eigenvalue problems. SIAM J. Appl. Math. 53(3), 799–828.CrossRefGoogle Scholar
Ward, M. J. & Keller, J. B. (1993) Strong localized perturbations of eigenvalue problems. SIAM J. Appl. Math. 53(3), 770–798.CrossRefGoogle Scholar