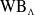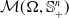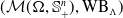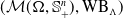1. Introduction
1.1. Classical optimal transport
Optimal transport (OT) [Reference Santambrogio87, Reference Villani89, Reference Villani90] provides a versatile framework for defining metrics and studying geometric structures on probability measures. It has been an active research area over the past decades with fruitful applications in various areas, including functional inequalities [Reference Lott and Villani68, Reference Otto and Villani76, Reference Sturm88], gradient flow [Reference Jordan, Kinderlehrer and Otto51, Reference Otto75], and more recently, image processing and machine learning [Reference Arjovsky, Chintala and Bottou3, Reference Ferradans, Papadakis, Peyré and Aujol37, Reference Frogner, Zhang, Mobahi, Araya and Poggio43]. The OT problem was first proposed by Monge in 1781 [Reference Monge72]: given probabilities
![]() $\rho _0$
and
$\rho _0$
and
![]() $\rho _1$
, find a measure-preserving transport map
$\rho _1$
, find a measure-preserving transport map
![]() $T$
minimising
$T$
minimising
However, its solution (i.e., the OT map) may not exist. This question remained open for a long time until 1942 when Kantorovich introduced a relaxed problem based on the so-called transport plans [Reference Kantorovich52]:
where
![]() $\pi _\#^x \gamma$
and
$\pi _\#^x \gamma$
and
![]() $\pi _\#^y \gamma$
are the first and second marginals of
$\pi _\#^y \gamma$
are the first and second marginals of
![]() $\gamma$
, respectively. The
$\gamma$
, respectively. The
![]() $2$
-Wasserstein distance (1.2) turns out to exhibit intriguing mathematical properties. Brenier [Reference Brenier14] proved that under mild conditions, the OT map
$2$
-Wasserstein distance (1.2) turns out to exhibit intriguing mathematical properties. Brenier [Reference Brenier14] proved that under mild conditions, the OT map
![]() $T$
to (1.1) exists and is uniquely given by the gradient of a convex function
$T$
to (1.1) exists and is uniquely given by the gradient of a convex function
![]() $\varphi$
. Thanks to the measure-preserving property of the transport map
$\varphi$
. Thanks to the measure-preserving property of the transport map
![]() $T = \nabla \varphi$
, it is easy to see that
$T = \nabla \varphi$
, it is easy to see that
![]() $\varphi$
satisfies the Monge–Ampère equation, which provides a PDE-based approach for solving the OT problem (1.1). One can also show that
$\varphi$
satisfies the Monge–Ampère equation, which provides a PDE-based approach for solving the OT problem (1.1). One can also show that
![]() $(\mathrm {id}, \nabla \varphi )_\# \rho _0$
gives a minimiser to (1.2). Equipped with the distance
$(\mathrm {id}, \nabla \varphi )_\# \rho _0$
gives a minimiser to (1.2). Equipped with the distance
![]() $\mathrm {W}_2(\cdot, \cdot )$
, the probability measure space becomes a geodesic space, where the geodesic is characterised by McCann’s displacement interpolation
$\mathrm {W}_2(\cdot, \cdot )$
, the probability measure space becomes a geodesic space, where the geodesic is characterised by McCann’s displacement interpolation
![]() $\rho _t\,:\!=\, ((1-t)I + t \nabla \varphi )_{\#}\rho _0$
[Reference McCann71]. In Benamou and Brenier’s seminal work [Reference Benamou and Brenier8], an equivalent fluid mechanics formulation was proposed for computational purposes:
$\rho _t\,:\!=\, ((1-t)I + t \nabla \varphi )_{\#}\rho _0$
[Reference McCann71]. In Benamou and Brenier’s seminal work [Reference Benamou and Brenier8], an equivalent fluid mechanics formulation was proposed for computational purposes:
This dynamic point of view has since stimulated numerous follow-up studies, including the present work. We refer the interested readers to [Reference Villani89, Reference Villani90] for the precise statements of aforementioned results and a detailed overview.
1.2. Unbalanced optimal transport
Although the OT theory has become a popular tool in learning theory and data science for its geometric nature and capacity for large-scale simulation, a limitation is that the associated metric is only defined for measures of equal mass, while in many applications, it is more desirable to allow measures with different masses. This leads to the problem of extending the classical OT theory to the unbalanced case. The early effort in this direction may date back to the works [Reference Kantorovich and Rubinshtein53, Reference Kantorovich and Rubinshtein54] by Kantorovich and Rubinshtein in the 1950s, where a simple static formulation with an extended Kantorovich norm was introduced. The underlying idea is to allow the mass to be sent to (or come from) a point at infinity, which was further investigated and extended in [Reference Guittet49, Reference Hanin50]. Similarly, Figalli and Gigli [Reference Figalli and Gigli39] introduced an unbalanced transportation distance via a variant of Kantorovich formulation (1.2) by allowing taking the mass from (or giving it back to) the boundary of the domain. Another closely related approach is the optimal partial transport [Reference Caffarelli and McCann20, Reference Figalli38], which is also based on (1.2) but involves a relaxed constraint
![]() $(\pi _\#^x \gamma, \pi _\#^y \gamma ) \le (\rho _0,\rho _1)$
and a shifted cost
$(\pi _\#^x \gamma, \pi _\#^y \gamma ) \le (\rho _0,\rho _1)$
and a shifted cost
![]() $|x-y|^2-\alpha$
.
$|x-y|^2-\alpha$
.
In addition to the static models, there is a large number of works devoted to defining an unbalanced OT model via a dynamic formulation in the spirit of [Reference Benamou and Brenier8]; see for example [Reference Benamou7, Reference Chizat, Peyré, Schmitzer and Vialard27, Reference Lombardi and Maitre66, Reference Maas, Rumpf, Schönlieb and Simon69, Reference Piccoli and Rossi79]. In these works, a source term and a corresponding penalisation term are introduced in the continuity equation and the action functional, respectively, in order to model the mass change. In particular, Piccoli and Rossi [Reference Piccoli and Rossi78, Reference Piccoli and Rossi79] defined a generalised Wasserstein distance by relaxing the marginal constraint
![]() $(\pi _\#^x \gamma, \pi _\#^y \gamma ) = (\rho _0,\rho _1)$
by a total variation regularisation, which turns out to be equivalent to the optimal partial transport in certain scenarios [Reference Chizat, Peyré, Schmitzer and Vialard27]. Moreover, an equivalent dynamic formulation has also been given in ref. [Reference Piccoli and Rossi79]. Later, a new transport model, called the Wasserstein–Fisher–Rao (WFR) or Hellinger–Kantorovich distance (in this work we adopt the former one), was introduced independently and almost simultaneously by three research groups with different perspectives and techniques [Reference Chizat, Peyré, Schmitzer and Vialard27, Reference Kondratyev, Monsaingeon and Vorotnikov56, Reference Liero, Mielke and Savaré64]. This model can be regarded as an inf-convolution of the Wasserstein and Fisher–Rao metric tensors, as the name suggests. In their subsequent work [Reference Chizat, Peyré, Schmitzer and Vialard29], Chizat et al. presented a class of unbalanced transport distances in a unified framework via both static and dynamic formulations, thanks to the notions of semi-couplings and Lagrangians. Meanwhile, Liero et al. [Reference Liero, Mielke and Savaré65] proposed a related optimal entropy-transport approach and discussed its properties in detail. It was proved that both the optimal partial transport and the WFR distance can be viewed as the special cases of the general frameworks in refs. [Reference Chizat, Peyré, Schmitzer and Vialard29, Reference Liero, Mielke and Savaré65]. After that, the unbalanced OT theory is further developed in various directions, such as gradient flows [Reference Kondratyev and Vorotnikov57, Reference Kondratyev and Vorotnikov59], Sobolev inequalities [Reference Kondratyev and Vorotnikov58] and the JKO scheme [Reference Fleissner41, Reference Gallouët and Monsaingeon44]. We also want to mention a recent work [Reference Lombardini and Rossi67] by Lombardini and Rossi, which gave a negative answer to an interesting question of whether it is possible to define an unbalanced transport distance that coincides with the Wasserstein one when the measures are of equal mass.
$(\pi _\#^x \gamma, \pi _\#^y \gamma ) = (\rho _0,\rho _1)$
by a total variation regularisation, which turns out to be equivalent to the optimal partial transport in certain scenarios [Reference Chizat, Peyré, Schmitzer and Vialard27]. Moreover, an equivalent dynamic formulation has also been given in ref. [Reference Piccoli and Rossi79]. Later, a new transport model, called the Wasserstein–Fisher–Rao (WFR) or Hellinger–Kantorovich distance (in this work we adopt the former one), was introduced independently and almost simultaneously by three research groups with different perspectives and techniques [Reference Chizat, Peyré, Schmitzer and Vialard27, Reference Kondratyev, Monsaingeon and Vorotnikov56, Reference Liero, Mielke and Savaré64]. This model can be regarded as an inf-convolution of the Wasserstein and Fisher–Rao metric tensors, as the name suggests. In their subsequent work [Reference Chizat, Peyré, Schmitzer and Vialard29], Chizat et al. presented a class of unbalanced transport distances in a unified framework via both static and dynamic formulations, thanks to the notions of semi-couplings and Lagrangians. Meanwhile, Liero et al. [Reference Liero, Mielke and Savaré65] proposed a related optimal entropy-transport approach and discussed its properties in detail. It was proved that both the optimal partial transport and the WFR distance can be viewed as the special cases of the general frameworks in refs. [Reference Chizat, Peyré, Schmitzer and Vialard29, Reference Liero, Mielke and Savaré65]. After that, the unbalanced OT theory is further developed in various directions, such as gradient flows [Reference Kondratyev and Vorotnikov57, Reference Kondratyev and Vorotnikov59], Sobolev inequalities [Reference Kondratyev and Vorotnikov58] and the JKO scheme [Reference Fleissner41, Reference Gallouët and Monsaingeon44]. We also want to mention a recent work [Reference Lombardini and Rossi67] by Lombardini and Rossi, which gave a negative answer to an interesting question of whether it is possible to define an unbalanced transport distance that coincides with the Wasserstein one when the measures are of equal mass.
1.3. Noncommutative optimal transport
More recently, there is also an increasing interest in generalising the OT theory to the noncommutative setting, namely, the quantum states or matrix-valued measures. The first line of research is motivated by the ergodicity of open quantum dynamics [Reference Gross48, Reference Kastoryano and Temme55, Reference Olkiewicz and Zegarlinski74]. In the seminal works [Reference Carlen and Maas21, Reference Carlen and Maas22] by Carlen and Maas, a quantum Wasserstein distance was introduced with a Benamou–Brenier dynamic formulation such that a primitive quantum Markov semigroup satisfying the detailed balance condition can be formulated as the gradient flow of the logarithmic relative entropy, which opens the door to investigating the noncommutative functional inequalities via the gradient flow techniques and the geodesic convexity; see for example [Reference Datta and Rouzé31, Reference Li and Lu62, Reference Rouzé and Datta84, Reference Wirth and Zhang93]. Meanwhile, Golse et al. proposed another quantum transport model via a generalised Monge–Kantorovich formulation, when they studied the mean-field and classical limits of the Schrödinger equation; see [Reference Golse, Mouhot and Paul45–Reference Golse and Paul47]. Other static quantum Wasserstein distances can be found in refs. [Reference Cole, Eckstein, Friedland and Życzkowski30, Reference De Palma, Marvian, Trevisan and Lloyd32, Reference De Palma and Trevisan33], just to name a few.
The second research line is driven by the advances in diffusion tensor imaging [Reference Bihan61, Reference Wandell92], where a tensor field (usually, a positive semi-definite matrix) is generated at each spatial position to encode the local diffusivity of water molecules in the brain. It gives rise to a natural question of how to compare two brain tensor fields, or mathematically how to define a reasonable distance between matrix-valued measures. Chen et al. [Reference Chen, Gangbo, Georgiou and Tannenbaum23, Reference Chen, Georgiou and Tannenbaum24] introduced a dynamic matricial Wasserstein distance for matrix-valued densities with unit mass, drawing inspiration from ref. [Reference Benamou and Brenier8] and leveraging the Lindblad equation in quantum mechanics, which was later extended to the unbalanced case [Reference Chen, Georgiou and Tannenbaum25] in a manner similar to [Reference Chizat, Peyré, Schmitzer and Vialard27]. In particular, Brenier and Vorotnikov [Reference Brenier and Vorotnikov16] recently proposed a different dynamic OT model for unbalanced matrix-valued measures called the Kantorovich–Bures metric, which is motivated by the observation in ref. [Reference Brenier15] that the incompressible Euler equation admits a dual concave maximisation problem. Regarding static formulations, Peyré et al. [Reference Peyré, Chizat, Vialard and Solomon77] introduced a quantum transport distance with entropic regularisation inspired by [Reference Liero, Mielke and Savaré65] and proposed an associated scaling algorithm that generalised the results in ref. [Reference Chizat, Peyré, Schmitzer and Vialard28]. Additionally, Ryu et al. defined a matrix OT model of order
![]() $1$
by a Beckmann-type flux formulation and presented a scalable and parallelisable numerical method. Applications in tensor field imaging were also explored in ref. [Reference Peyré, Chizat, Vialard and Solomon77, Reference Ryu, Chen, Li and Osher86].
$1$
by a Beckmann-type flux formulation and presented a scalable and parallelisable numerical method. Applications in tensor field imaging were also explored in ref. [Reference Peyré, Chizat, Vialard and Solomon77, Reference Ryu, Chen, Li and Osher86].
1.4. Contribution
The initial motivation for this work is the numerical study of the unbalanced matricial OT models proposed in ref. [Reference Brenier and Vorotnikov16, Reference Chen, Georgiou and Tannenbaum25]; see (𝒫WB
) and (𝒫2,FR
). We find that despite their distinct formulations, these models actually share many mathematical properties. In this work, we consider an abstract continuity equation
![]() $\partial _t \mathsf {G} + \mathsf {D} \mathsf {q} = \mathsf {R}^{{\mathrm {sym}}}$
in Definition3.4 with
$\partial _t \mathsf {G} + \mathsf {D} \mathsf {q} = \mathsf {R}^{{\mathrm {sym}}}$
in Definition3.4 with
![]() $\mathsf {D}$
being a first-order constant coefficient linear differential operator such that
$\mathsf {D}$
being a first-order constant coefficient linear differential operator such that
![]() $\mathsf {D}^*(I) = 0$
, in analogy with the one
$\mathsf {D}^*(I) = 0$
, in analogy with the one
![]() $\partial _t \mathsf {G} + 2 (\mathsf {L}^* \circ \mathsf {P})\, \mathsf {q} = 0$
for the matrix-valued optimal ballistic transport problem (cf. [Reference Vorotnikov91, (1.4)–(1.5)]). Here,
$\partial _t \mathsf {G} + 2 (\mathsf {L}^* \circ \mathsf {P})\, \mathsf {q} = 0$
for the matrix-valued optimal ballistic transport problem (cf. [Reference Vorotnikov91, (1.4)–(1.5)]). Here,
![]() $\mathsf {q}(t,x)$
can be intuitively seen as a momentum variable;
$\mathsf {q}(t,x)$
can be intuitively seen as a momentum variable;
![]() $\mathsf {D}q$
is the matricial analogue of the advection term
$\mathsf {D}q$
is the matricial analogue of the advection term
![]() $\mathrm {div}\, m$
in (𝒫W2
) controlling the mass transportation in space and between components;
$\mathrm {div}\, m$
in (𝒫W2
) controlling the mass transportation in space and between components;
![]() $\mathsf {R}^{{\mathrm {sym}}}$
is the reaction part describing the variation of mass. Then, thanks to the weighted infinitesimal cost
$\mathsf {R}^{{\mathrm {sym}}}$
is the reaction part describing the variation of mass. Then, thanks to the weighted infinitesimal cost
![]() $J_\Lambda (G_t, q_t, R_t) =\frac {1}{2} (q_t \Lambda _1^\dagger ) \cdot G_t^{\dagger } (q_t \Lambda _1^\dagger ) + \frac {1}{2} (R_t \Lambda _2^\dagger ) \cdot G^{\dagger }_t (R_t \Lambda _2^\dagger )$
given in Proposition3.1 with the weight matrices
$J_\Lambda (G_t, q_t, R_t) =\frac {1}{2} (q_t \Lambda _1^\dagger ) \cdot G_t^{\dagger } (q_t \Lambda _1^\dagger ) + \frac {1}{2} (R_t \Lambda _2^\dagger ) \cdot G^{\dagger }_t (R_t \Lambda _2^\dagger )$
given in Proposition3.1 with the weight matrices
![]() $\Lambda _1$
and
$\Lambda _1$
and
![]() $\Lambda _2$
representing the contributions of each component of
$\Lambda _2$
representing the contributions of each component of
![]() $q$
and
$q$
and
![]() $G$
in
$G$
in
![]() $J_\Lambda$
, we define a general matrix-valued unbalanced OT distance
$J_\Lambda$
, we define a general matrix-valued unbalanced OT distance
![]() $\mathrm {WB}_{\Lambda }(\cdot, \cdot )$
(𝒫) as a convex optimisation, similarly to the classical case (𝒫W2
), which we call the weighted Wasserstein–-Bures distance; see Definition3.8. We note that the problems (𝒫WB
) and (𝒫2,FR
), as well as the scalar WFR distance (𝒫WFR
), can be viewed as the special instances of our model (𝒫). See Section 7 for more details.
$\mathrm {WB}_{\Lambda }(\cdot, \cdot )$
(𝒫) as a convex optimisation, similarly to the classical case (𝒫W2
), which we call the weighted Wasserstein–-Bures distance; see Definition3.8. We note that the problems (𝒫WB
) and (𝒫2,FR
), as well as the scalar WFR distance (𝒫WFR
), can be viewed as the special instances of our model (𝒫). See Section 7 for more details.
Our main contribution is a comprehensive and self-contained study of the properties of the weighted distance
![]() $\mathrm {WB}_{\Lambda }$
on the positive semi-definite matrix-valued Radon measure space
$\mathrm {WB}_{\Lambda }$
on the positive semi-definite matrix-valued Radon measure space
![]() $\mathcal {M}(\Omega, \mathbb {S}_+^n)$
. We establish the a priori estimates for solutions of the abstract continuity equation (3.13) in Lemmas3.9, 3.12 and Proposition3.13, which consequently gives the well-posedness of the model (𝒫) and a useful compactness result (Proposition3.18). Then, by leveraging tools from convex analysis, we show the existence of the minimiser (i.e., the minimising geodesic) to (𝒫) with a characterisation of the optimality conditions; see Theorems4.2 and 4.5. Moreover, we prove that the topology induced by
$\mathcal {M}(\Omega, \mathbb {S}_+^n)$
. We establish the a priori estimates for solutions of the abstract continuity equation (3.13) in Lemmas3.9, 3.12 and Proposition3.13, which consequently gives the well-posedness of the model (𝒫) and a useful compactness result (Proposition3.18). Then, by leveraging tools from convex analysis, we show the existence of the minimiser (i.e., the minimising geodesic) to (𝒫) with a characterisation of the optimality conditions; see Theorems4.2 and 4.5. Moreover, we prove that the topology induced by
![]() $\mathrm {WB}_\Lambda (\cdot, \cdot )$
is stronger than the weak* one, and study the limit model when a weight matrix goes to zero; see Propositions5.2 and 4.6, respectively. With the help of these results, in Theorem5.5 and Corollary5.7, we characterise the absolutely continuous curve with respect to the metric
$\mathrm {WB}_\Lambda (\cdot, \cdot )$
is stronger than the weak* one, and study the limit model when a weight matrix goes to zero; see Propositions5.2 and 4.6, respectively. With the help of these results, in Theorem5.5 and Corollary5.7, we characterise the absolutely continuous curve with respect to the metric
![]() $\mathrm {WB}_\Lambda$
and show that
$\mathrm {WB}_\Lambda$
and show that
![]() $(\mathcal {M}(\Omega, \mathbb {S}_+^n), \mathrm {WB}_\Lambda )$
is a complete geodesic space. We further consider its conic structure and prove in Theorem6.3 that the space
$(\mathcal {M}(\Omega, \mathbb {S}_+^n), \mathrm {WB}_\Lambda )$
is a complete geodesic space. We further consider its conic structure and prove in Theorem6.3 that the space
![]() $(\mathcal {M}(\Omega, \mathbb {S}_+^n), \mathrm {WB}_\Lambda )$
is a metric cone over
$(\mathcal {M}(\Omega, \mathbb {S}_+^n), \mathrm {WB}_\Lambda )$
is a metric cone over
![]() $(\mathcal {M}_1, \mathrm {SWB}_\Lambda )$
, where
$(\mathcal {M}_1, \mathrm {SWB}_\Lambda )$
, where
![]() $\mathcal {M}_1$
is a normalised matrix-valued measure space (6.2), which corresponds to a noncommutative probability space, and
$\mathcal {M}_1$
is a normalised matrix-valued measure space (6.2), which corresponds to a noncommutative probability space, and
![]() $\mathrm {SWB}_\Lambda$
is the spherical distance (6.1) induced by
$\mathrm {SWB}_\Lambda$
is the spherical distance (6.1) induced by
![]() $\mathrm {WB}_\Lambda$
. Recalling the Riemannian interpretation in Corollary5.8, we can formally view
$\mathrm {WB}_\Lambda$
. Recalling the Riemannian interpretation in Corollary5.8, we can formally view
![]() $(\mathcal {M}(\Omega, \mathbb {S}_+^n), \mathrm {WB}_\Lambda )$
as a Riemannian manifold and
$(\mathcal {M}(\Omega, \mathbb {S}_+^n), \mathrm {WB}_\Lambda )$
as a Riemannian manifold and
![]() $\mathcal {M}_1$
as its submanifold with the induced metric
$\mathcal {M}_1$
as its submanifold with the induced metric
![]() $\mathrm {SWB}_\Lambda$
, which allows developing the Otto calculus in the spirit of [Reference Otto and Villani76]. These results can be readily applied to the models (𝒫WB
) and (𝒫2,FR
), which lay a solid mathematical foundation for the distance (𝒫2,FR
) and complement the results in ref. [Reference Brenier and Vorotnikov16] for (𝒫WB
) (note that our approach is quite different from theirs).
$\mathrm {SWB}_\Lambda$
, which allows developing the Otto calculus in the spirit of [Reference Otto and Villani76]. These results can be readily applied to the models (𝒫WB
) and (𝒫2,FR
), which lay a solid mathematical foundation for the distance (𝒫2,FR
) and complement the results in ref. [Reference Brenier and Vorotnikov16] for (𝒫WB
) (note that our approach is quite different from theirs).
In the companion work [Reference Li and Zou63], we have designed a convergent discretisation scheme for the general model (𝒫), which directly applies to the Kantorovich–Bures distance (𝒫WB ) [Reference Brenier and Vorotnikov16], the matricial interpolation distance (𝒫2,FR ) [Reference Chen, Georgiou and Tannenbaum25] and the WFR metric (𝒫WFR ) [Reference Chizat, Peyré, Schmitzer and Vialard27], thanks to the discussion in Section 7 of the present work.
1.5. Layout
The rest of this work is organised as follows. In Section 2, we give a list of basic notations that will be used throughout this work and recall some preliminary results. In Section 3, we define a class of weighted Wasserstein–Bures distances for matrix-valued measures via a dynamic formulation. Sections 4 and 5 are devoted to its topological, metric and geometric properties, while in Section 6, we discuss its conic structure. In Section 7, we connect our general model with several existing models in the literature. Some auxiliary proofs are included in Appendix A.
2. Preliminaries and notation
2.1. Notation and convention
-
• We denote by
 $\mathbb {R}^{n \times m}$
the space of
$\mathbb {R}^{n \times m}$
the space of
 $n \times m$
real matrices. If
$n \times m$
real matrices. If
 $m = n$
, we simply write it as
$m = n$
, we simply write it as
 $\mathbb {M}^{n}$
. Moreover, we use
$\mathbb {M}^{n}$
. Moreover, we use
 $\mathbb {S}^n$
,
$\mathbb {S}^n$
,
 $\mathbb {S}_+^n$
and
$\mathbb {S}_+^n$
and
 $\mathbb {S}^n_{++}$
to denote symmetric matrices, positive semi-definite matrices and positive definite matrices, respectively.
$\mathbb {S}^n_{++}$
to denote symmetric matrices, positive semi-definite matrices and positive definite matrices, respectively.
 $\mathbb {A}^n$
denotes the space of
$\mathbb {A}^n$
denotes the space of
 $n \times n$
antisymmetric matrices.
$n \times n$
antisymmetric matrices. -
• We denote by
 $|\cdot |$
the Euclidean norm on
$|\cdot |$
the Euclidean norm on
 $\mathbb {R}^n$
. We equip the matrix space
$\mathbb {R}^n$
. We equip the matrix space
 $\mathbb {R}^{n \times m}$
with the Frobenius inner product
$\mathbb {R}^{n \times m}$
with the Frobenius inner product
 $A \cdot B = Tr(A^{\mathrm {T}} B)$
and the associated norm
$A \cdot B = Tr(A^{\mathrm {T}} B)$
and the associated norm
 $\lVert A \rVert _{\mathrm {F}} = \sqrt { A \cdot A}$
.
$\lVert A \rVert _{\mathrm {F}} = \sqrt { A \cdot A}$
. -
• The symmetric and antisymmetric parts of
 $A \in \mathbb {M}^n$
are given by(2.1)respectively. We also write
$A \in \mathbb {M}^n$
are given by(2.1)respectively. We also write \begin{equation} A^{\mathrm {sym}} = (A + A^{\mathrm {T}})/2\,,\quad A^{\mathrm {ant}} = (A - A^{\mathrm {T}})/2\,, \end{equation}
\begin{equation} A^{\mathrm {sym}} = (A + A^{\mathrm {T}})/2\,,\quad A^{\mathrm {ant}} = (A - A^{\mathrm {T}})/2\,, \end{equation}
 $A \preceq B$
(resp.,
$A \preceq B$
(resp.,
 $A \prec B$
) for
$A \prec B$
) for
 $A, B \in \mathbb {S}^n$
if
$A, B \in \mathbb {S}^n$
if
 $B - A \in \mathbb {S}^n_+$
(resp.,
$B - A \in \mathbb {S}^n_+$
(resp.,
 $B - A \in \mathbb {S}^n_{++}$
).
$B - A \in \mathbb {S}^n_{++}$
).
-
•
 $\mathcal {X}$
denotes a generic compact separable metric space with Borel
$\mathcal {X}$
denotes a generic compact separable metric space with Borel
 $\sigma$
-algebra
$\sigma$
-algebra
 $\mathscr {B}(\mathcal {X})$
, unless otherwise specified.
$\mathscr {B}(\mathcal {X})$
, unless otherwise specified. -
•
 $C(\mathcal {X},\mathbb {R}^n)$
denotes the space of
$C(\mathcal {X},\mathbb {R}^n)$
denotes the space of
 $\mathbb {R}^n$
-valued continuous functions on
$\mathbb {R}^n$
-valued continuous functions on
 $\mathcal {X}$
with the supremum norm
$\mathcal {X}$
with the supremum norm
 $\lVert \cdot \rVert _\infty$
. Its dual space, denoted by
$\lVert \cdot \rVert _\infty$
. Its dual space, denoted by
 $\mathcal {M}(\mathcal {X},\mathbb {R}^n)$
, is
$\mathcal {M}(\mathcal {X},\mathbb {R}^n)$
, is
 $\mathbb {R}^n$
-valued Radon measure space with the total variation norm
$\mathbb {R}^n$
-valued Radon measure space with the total variation norm
 $\lVert \cdot \rVert _{\mathrm {TV}}$
.
$\lVert \cdot \rVert _{\mathrm {TV}}$
. -
• Let
 $\mathcal {B}$
be a Banach space with the dual space
$\mathcal {B}$
be a Banach space with the dual space
 $\mathcal {B}^*$
. We denote by
$\mathcal {B}^*$
. We denote by
 $\langle \cdot, \cdot \rangle _{\mathcal {B}}$
the duality pairing between
$\langle \cdot, \cdot \rangle _{\mathcal {B}}$
the duality pairing between
 $\mathcal {B}$
and
$\mathcal {B}$
and
 $\mathcal {B}^*$
. When
$\mathcal {B}^*$
. When
 $\mathcal {B} = C(\mathcal {X},\mathbb {R}^n)$
, we usually write it as
$\mathcal {B} = C(\mathcal {X},\mathbb {R}^n)$
, we usually write it as
 $\langle \cdot, \cdot \rangle _{\mathcal {X}}$
for short. We will also consider the weak and weak* convergences on
$\langle \cdot, \cdot \rangle _{\mathcal {X}}$
for short. We will also consider the weak and weak* convergences on
 $\mathcal {B}$
and
$\mathcal {B}$
and
 $\mathcal {B}^*$
, respectively. In particular, a sequence of measures
$\mathcal {B}^*$
, respectively. In particular, a sequence of measures
 $\{\mu _j\}$
weak* converges to
$\{\mu _j\}$
weak* converges to
 $\mu \in \mathcal {M}(\mathcal {X},\mathbb {R}^n)$
if for any
$\mu \in \mathcal {M}(\mathcal {X},\mathbb {R}^n)$
if for any
 $\phi \in C(\mathcal {X},\mathbb {R}^n)$
, there holds
$\phi \in C(\mathcal {X},\mathbb {R}^n)$
, there holds
 $\langle \mu _j, \phi \rangle _{\mathcal {X}} \to \langle \mu, \phi \rangle _{\mathcal {X}}$
as
$\langle \mu _j, \phi \rangle _{\mathcal {X}} \to \langle \mu, \phi \rangle _{\mathcal {X}}$
as
 $j \to +\infty$
.
$j \to +\infty$
. -
• Let
 $\mathbb {R}_+\,:\!=\, [0,\infty )$
, and
$\mathbb {R}_+\,:\!=\, [0,\infty )$
, and
 $\mathcal {M}(\mathcal {X},\mathbb {R}_+)$
be the space of nonnegative finite Radon measures. For
$\mathcal {M}(\mathcal {X},\mathbb {R}_+)$
be the space of nonnegative finite Radon measures. For
 $\mu \in \mathcal {M}(\mathcal {X},\mathbb {R}^n)$
, we have an associated variation measure
$\mu \in \mathcal {M}(\mathcal {X},\mathbb {R}^n)$
, we have an associated variation measure
 $|\mu |\in \mathcal {M}(\mathcal {X},\mathbb {R}_+)$
such that
$|\mu |\in \mathcal {M}(\mathcal {X},\mathbb {R}_+)$
such that
 $\mathrm {d} \mu = \sigma \mathrm {d} |\mu |$
with
$\mathrm {d} \mu = \sigma \mathrm {d} |\mu |$
with
 $|\sigma (x)| = 1$
for
$|\sigma (x)| = 1$
for
 $|\mu |$
-a.e.
$|\mu |$
-a.e.
 $x \in \mathcal {X}$
, where
$x \in \mathcal {X}$
, where
 $\sigma \,:\, \mathcal {X} \to \mathbb {R}^n$
is the Radon–Nikodym derivative (density) of
$\sigma \,:\, \mathcal {X} \to \mathbb {R}^n$
is the Radon–Nikodym derivative (density) of
 $\mu$
with respect to
$\mu$
with respect to
 $|\mu |$
[Reference Evans and Gariepy36, Reference Rudin85].
$|\mu |$
[Reference Evans and Gariepy36, Reference Rudin85]. -
• We identify the space of matrix-valued Radon measures
 $\mathcal {M}(\mathcal {X},\mathbb {R}^{n \times m})$
with
$\mathcal {M}(\mathcal {X},\mathbb {R}^{n \times m})$
with
 $\mathcal {M}(\mathcal {X},\mathbb {R}^{nm})$
by vectorisation. It is easy to see that both sets of
$\mathcal {M}(\mathcal {X},\mathbb {R}^{nm})$
by vectorisation. It is easy to see that both sets of
 $\mathbb {S}^n$
-valued Radon measures
$\mathbb {S}^n$
-valued Radon measures
 $\mathcal {M}(\mathcal {X},\mathbb {S}^n)$
and
$\mathcal {M}(\mathcal {X},\mathbb {S}^n)$
and
 $\mathbb {S}^n_+$
-valued Radon measures
$\mathbb {S}^n_+$
-valued Radon measures
 $\mathcal {M}(\mathcal {X},\mathbb {S}_+^n)$
are closed in
$\mathcal {M}(\mathcal {X},\mathbb {S}_+^n)$
are closed in
 $\mathcal {M}(\mathcal {X},\mathbb {M}^n)$
with respect to the weak* topology [Reference Duran and Lopez-Rodriguez35, Theorem 3.5]. Moreover, we have the following characterisation:where
$\mathcal {M}(\mathcal {X},\mathbb {M}^n)$
with respect to the weak* topology [Reference Duran and Lopez-Rodriguez35, Theorem 3.5]. Moreover, we have the following characterisation:where \begin{equation*} (C(\mathcal {X}, \mathbb {S}^n))^* \simeq (C(\mathcal {X},\mathbb {M}^n) /C(\mathcal {X}, \mathbb {A}^n))^* \simeq \mathcal {M}(\mathcal {X}, \mathbb {S}^n)\,, \end{equation*}
\begin{equation*} (C(\mathcal {X}, \mathbb {S}^n))^* \simeq (C(\mathcal {X},\mathbb {M}^n) /C(\mathcal {X}, \mathbb {A}^n))^* \simeq \mathcal {M}(\mathcal {X}, \mathbb {S}^n)\,, \end{equation*}
 $\simeq$
means the isometric isomorphism and
$\simeq$
means the isometric isomorphism and
 $C(\mathcal {X},\mathbb {M}^n) /C(\mathcal {X}, \mathbb {A}^n)$
is the quotient space. Indeed, we observe that
$C(\mathcal {X},\mathbb {M}^n) /C(\mathcal {X}, \mathbb {A}^n)$
is the quotient space. Indeed, we observe that
 $\mu \in \mathcal {M}(\mathcal {X},\mathbb {S}^n) \subset \mathcal {M}(\mathcal {X},\mathbb {M}^n) \simeq C(\mathcal {X},\mathbb {M}^n)^*$
if and only if its induced linear functional on
$\mu \in \mathcal {M}(\mathcal {X},\mathbb {S}^n) \subset \mathcal {M}(\mathcal {X},\mathbb {M}^n) \simeq C(\mathcal {X},\mathbb {M}^n)^*$
if and only if its induced linear functional on
 $C(\mathcal {X},\mathbb {M}^n)$
has the kernel
$C(\mathcal {X},\mathbb {M}^n)$
has the kernel
 $C(\mathcal {X}, \mathbb {A}^n)$
, which yields, by [Reference Brezis17, Proposition 11.9],Meanwhile,
$C(\mathcal {X}, \mathbb {A}^n)$
, which yields, by [Reference Brezis17, Proposition 11.9],Meanwhile, \begin{equation*} (C(\mathcal {X},\mathbb {M}^n) /C(\mathcal {X}, \mathbb {A}^n))^* \simeq \mathcal {M}(\mathcal {X}, \mathbb {S}^n)\,. \end{equation*}
\begin{equation*} (C(\mathcal {X},\mathbb {M}^n) /C(\mathcal {X}, \mathbb {A}^n))^* \simeq \mathcal {M}(\mathcal {X}, \mathbb {S}^n)\,. \end{equation*}
 $C(\mathcal {X}, \mathbb {S}^n) \simeq C(\mathcal {X},\mathbb {M}^n) /C(\mathcal {X}, \mathbb {A}^n)$
is a consequence of
$C(\mathcal {X}, \mathbb {S}^n) \simeq C(\mathcal {X},\mathbb {M}^n) /C(\mathcal {X}, \mathbb {A}^n)$
is a consequence of
 $\mathbb {S}^n \perp \mathbb {A}^n$
and
$\mathbb {S}^n \perp \mathbb {A}^n$
and
 $\mathbb {S}^n \simeq \mathbb {M}^n/\mathbb {A}^n$
.
$\mathbb {S}^n \simeq \mathbb {M}^n/\mathbb {A}^n$
.
-
• For
 $\mu \in \mathcal {M}(\mathcal {X}, \mathbb {S}_+^n)$
, we define an associated trace measure
$\mu \in \mathcal {M}(\mathcal {X}, \mathbb {S}_+^n)$
, we define an associated trace measure
 $Tr\mu$
by the set function
$Tr\mu$
by the set function
 $E \to Tr (\mu (E))$
,
$E \to Tr (\mu (E))$
,
 $E \in \mathscr {B}(\mathcal {X})$
. It is clear that
$E \in \mathscr {B}(\mathcal {X})$
. It is clear that
 $ 0 \preceq \mu (E) \preceq Tr (\mu (E)) I$
and
$ 0 \preceq \mu (E) \preceq Tr (\mu (E)) I$
and
 $ Tr\mu$
is equivalent to
$ Tr\mu$
is equivalent to
 $|\mu |$
, denoted by
$|\mu |$
, denoted by
 $Tr\mu \sim |\mu |$
. That is,(2.2)We will usually use
$Tr\mu \sim |\mu |$
. That is,(2.2)We will usually use \begin{equation} |\mu | \ll Tr\mu \quad \text {and} \quad Tr\mu \ll |\mu |\,. \end{equation}
\begin{equation} |\mu | \ll Tr\mu \quad \text {and} \quad Tr\mu \ll |\mu |\,. \end{equation}
 $Tr\mu$
as the dominant measure for
$Tr\mu$
as the dominant measure for
 $\mu \in \mathcal {M}(\mathcal {X},\mathbb {S}_+^n)$
. In addition, note that for
$\mu \in \mathcal {M}(\mathcal {X},\mathbb {S}_+^n)$
. In addition, note that for
 $\lambda \in \mathcal {M}(\mathcal {X}, \mathbb {R}_+)$
with
$\lambda \in \mathcal {M}(\mathcal {X}, \mathbb {R}_+)$
with
 $|\mu | \ll \lambda$
, there holds
$|\mu | \ll \lambda$
, there holds
 $\frac {\mathrm {d} \mu }{\mathrm {d} \lambda } \in \mathbb {S}^n_+$
for
$\frac {\mathrm {d} \mu }{\mathrm {d} \lambda } \in \mathbb {S}^n_+$
for
 $\lambda$
-a.e.
$\lambda$
-a.e.
 $x \in \mathcal {X}$
, which is an equivalent characterisation of
$x \in \mathcal {X}$
, which is an equivalent characterisation of
 $\mathcal {M}(\mathcal {X}, \mathbb {S}_+^n)$
.
$\mathcal {M}(\mathcal {X}, \mathbb {S}_+^n)$
.
-
• We will use sans serif letterforms to denote vector-valued or matrix-valued measures, e.g.,
 $\mathsf {A} \in \mathcal {M}(\mathcal {X}, \mathbb {M}^n)$
, while letters with serifs are reserved for their densities with respect to some reference measure, e.g.,
$\mathsf {A} \in \mathcal {M}(\mathcal {X}, \mathbb {M}^n)$
, while letters with serifs are reserved for their densities with respect to some reference measure, e.g.,
 $A_\lambda \,:\!=\, \frac {\mathrm {d} \mathsf {A}}{\mathrm {d} \lambda }$
for
$A_\lambda \,:\!=\, \frac {\mathrm {d} \mathsf {A}}{\mathrm {d} \lambda }$
for
 $|\mathsf {A}| \ll \lambda$
. The symmetric and antisymmetric parts
$|\mathsf {A}| \ll \lambda$
. The symmetric and antisymmetric parts
 $\mathsf {A}^{\mathrm {sym}}$
and
$\mathsf {A}^{\mathrm {sym}}$
and
 $\mathsf {A}^{\mathrm {ant}}$
of
$\mathsf {A}^{\mathrm {ant}}$
of
 $\mathsf {A} \in \mathcal {M}(\mathcal {X}, \mathbb {M}^n)$
are defined as in (2.1).
$\mathsf {A} \in \mathcal {M}(\mathcal {X}, \mathbb {M}^n)$
are defined as in (2.1). -
• We identify a measure and its density with respect to the Lebesgue measure (if exists) unless otherwise specified.
-
• For
 $\lambda \in \mathcal {M}(\mathcal {X}, \mathbb {R}_+)$
, we denote by
$\lambda \in \mathcal {M}(\mathcal {X}, \mathbb {R}_+)$
, we denote by
 $L^p_\lambda (\mathcal {X},\mathbb {R}^n)$
with
$L^p_\lambda (\mathcal {X},\mathbb {R}^n)$
with
 $p \in [1, +\infty ]$
the standard space of
$p \in [1, +\infty ]$
the standard space of
 $p$
-integrable
$p$
-integrable
 $\mathbb {R}^n$
-valued functions. For
$\mathbb {R}^n$
-valued functions. For
 $\mathsf {G} \in \mathcal {M}(\mathcal {X}, \mathbb {S}_+^n)$
, we consider the space of
$\mathsf {G} \in \mathcal {M}(\mathcal {X}, \mathbb {S}_+^n)$
, we consider the space of
 $\mathbb {R}^{n \times m}$
-valued measurable functions endowed with the semi-inner product:(2.3)where
$\mathbb {R}^{n \times m}$
-valued measurable functions endowed with the semi-inner product:(2.3)where \begin{equation} \langle P, Q \rangle _{L^2_{\mathsf {G}}(\mathcal {X})} \,:\!=\, \langle \mathsf {G}, QP^{\mathrm {T}} \rangle _{\mathcal {X}} = \int _{\mathcal {X}} P \cdot (\mathrm {d} \mathsf {G}\, Q) = \int _{\mathcal {X}} P \cdot \big (G_\lambda Q \big )\, \mathrm {d} \lambda \,, \end{equation}
\begin{equation} \langle P, Q \rangle _{L^2_{\mathsf {G}}(\mathcal {X})} \,:\!=\, \langle \mathsf {G}, QP^{\mathrm {T}} \rangle _{\mathcal {X}} = \int _{\mathcal {X}} P \cdot (\mathrm {d} \mathsf {G}\, Q) = \int _{\mathcal {X}} P \cdot \big (G_\lambda Q \big )\, \mathrm {d} \lambda \,, \end{equation}
 $\lambda$
is a reference measure such that
$\lambda$
is a reference measure such that
 $|\mathsf {G}|\ll \lambda$
and
$|\mathsf {G}|\ll \lambda$
and
 $G_\lambda$
is the density. Noting that
$G_\lambda$
is the density. Noting that
 $\lVert Q \rVert _{L^2_{\mathsf {G}}(\mathcal {X})} = 0$
is equivalent to
$\lVert Q \rVert _{L^2_{\mathsf {G}}(\mathcal {X})} = 0$
is equivalent to
 $G_\lambda Q = 0$
for
$G_\lambda Q = 0$
for
 $\lambda$
-a.e.
$\lambda$
-a.e.
 $x \in \mathcal {X}$
, the kernel of the seminorm
$x \in \mathcal {X}$
, the kernel of the seminorm
 $\lVert \cdot \rVert _{L^2_{\mathsf {G}}(\mathcal {X})}$
is given by
$\lVert \cdot \rVert _{L^2_{\mathsf {G}}(\mathcal {X})}$
is given by
 $\{Q\,;\ \mathrm {Ran}(Q) \in \mathrm {Ker}(G_\lambda )\,, \,\lambda \text {-a.e.}\}$
. Then, we define the Hilbert space
$\{Q\,;\ \mathrm {Ran}(Q) \in \mathrm {Ker}(G_\lambda )\,, \,\lambda \text {-a.e.}\}$
. Then, we define the Hilbert space
 $L^2_{\mathsf {G}}(\mathcal {X}, \mathbb {R}^{n \times m})$
as the quotient space by
$L^2_{\mathsf {G}}(\mathcal {X}, \mathbb {R}^{n \times m})$
as the quotient space by
 $\mathrm {Ker}\big (\lVert \cdot \rVert _{L^2_{\mathsf {G}}(\mathcal {X})}\big )$
.
$\mathrm {Ker}\big (\lVert \cdot \rVert _{L^2_{\mathsf {G}}(\mathcal {X})}\big )$
.
2.2. Preliminaries
We denote by
![]() $A^\dagger \in \mathbb {R}^{m \times n}$
the pseudoinverse of a matrix
$A^\dagger \in \mathbb {R}^{m \times n}$
the pseudoinverse of a matrix
![]() $A \in \mathbb {R}^{n \times m}$
. If
$A \in \mathbb {R}^{n \times m}$
. If
![]() $A \in \mathbb {S}^n$
has the eigendecomposition
$A \in \mathbb {S}^n$
has the eigendecomposition
![]() $A = O \Sigma O^{\mathrm {T}}$
, then
$A = O \Sigma O^{\mathrm {T}}$
, then
![]() $A^\dagger = O \Sigma ^\dagger O^{\mathrm {T}}$
with
$A^\dagger = O \Sigma ^\dagger O^{\mathrm {T}}$
with
![]() $\Sigma ^\dagger = \text {diag}(\lambda _1^{-1}, \ldots, \lambda _s^{-1},0, \ldots, 0)$
, where
$\Sigma ^\dagger = \text {diag}(\lambda _1^{-1}, \ldots, \lambda _s^{-1},0, \ldots, 0)$
, where
![]() $O$
is an orthogonal matrix and
$O$
is an orthogonal matrix and
![]() $\Sigma = \text {diag}(\lambda _1,\ldots, \lambda _s,0, \ldots, 0)$
is a diagonal matrix with
$\Sigma = \text {diag}(\lambda _1,\ldots, \lambda _s,0, \ldots, 0)$
is a diagonal matrix with
![]() $\{\lambda _i\}$
being nonzero eigenvalues of
$\{\lambda _i\}$
being nonzero eigenvalues of
![]() $A$
.
$A$
.
Lemma 2.1. The following properties hold:
-
1. If
 $A \succeq B \succeq 0$
and
$A \succeq B \succeq 0$
and
 $\mathrm {Ran}(A) = \mathrm {Ran}(B)$
, then
$\mathrm {Ran}(A) = \mathrm {Ran}(B)$
, then
 $B^{\dagger } \succeq A^{\dagger }$
.
$B^{\dagger } \succeq A^{\dagger }$
. -
2. The cone
 $\mathbb {S}^n_+$
in
$\mathbb {S}^n_+$
in
 $\mathbb {S}^n$
is self-dual, that is,
$\mathbb {S}^n$
is self-dual, that is,
 $(\mathbb {S}_+^n)^* \,:\!=\, \{B\in \mathbb {S}^n\,; \ Tr(AB) \ge 0\,,\ \forall A \in \mathbb {S}^n_+ \} = \mathbb {S}^n_+$
.
$(\mathbb {S}_+^n)^* \,:\!=\, \{B\in \mathbb {S}^n\,; \ Tr(AB) \ge 0\,,\ \forall A \in \mathbb {S}^n_+ \} = \mathbb {S}^n_+$
. -
3. If
 $A, B \succeq 0$
and
$A, B \succeq 0$
and
 $A \cdot B = 0$
, then
$A \cdot B = 0$
, then
 $\mathrm {Ran} B \subset \mathrm {Ker} A$
, equivalently,
$\mathrm {Ran} B \subset \mathrm {Ker} A$
, equivalently,
 $\mathrm {Ran} A \subset \mathrm {Ker} B$
.
$\mathrm {Ran} A \subset \mathrm {Ker} B$
. -
4. For
 $A \in \mathbb {S}_+^n, M \in \mathbb {R}^{n \times m}$
, there holds
(2.4)
$A \in \mathbb {S}_+^n, M \in \mathbb {R}^{n \times m}$
, there holds
(2.4) \begin{equation} (A M) \cdot M \le Tr(A)\lVert M \rVert _{\mathrm {F}}^2\,. \end{equation}
\begin{equation} (A M) \cdot M \le Tr(A)\lVert M \rVert _{\mathrm {F}}^2\,. \end{equation}
Remark 2.2. The range condition
![]() $\mathrm {Ran}(A) = \mathrm {Ran}(B)$
for the first statement in Lemma 2.1 above is necessary, due to the example
$\mathrm {Ran}(A) = \mathrm {Ran}(B)$
for the first statement in Lemma 2.1 above is necessary, due to the example
![]() $A = \text {diag}(1,1,1,0)$
and
$A = \text {diag}(1,1,1,0)$
and
![]() $B = \text {diag}(1,1,0,0)$
. Moreover, we remark that for
$B = \text {diag}(1,1,0,0)$
. Moreover, we remark that for
![]() $\mathsf {G} \in \mathcal {M}(\mathcal {X}, \mathbb {S}_+^n)$
, there holds
$\mathsf {G} \in \mathcal {M}(\mathcal {X}, \mathbb {S}_+^n)$
, there holds
![]() $L_{Tr \mathsf {G}}^2(\mathcal {X}, \mathbb {R}^n) \subset L_{\mathsf {G}}^2(\mathcal {X}, \mathbb {R}^n)$
by (2.4), while the converse is not true; see [35] for the counterexample.
$L_{Tr \mathsf {G}}^2(\mathcal {X}, \mathbb {R}^n) \subset L_{\mathsf {G}}^2(\mathcal {X}, \mathbb {R}^n)$
by (2.4), while the converse is not true; see [35] for the counterexample.
Proof. We only prove the first statement, as the others are direct. We first note that the orthogonal projection onto
![]() $\mathrm {Ran}(A) = \mathrm {Ran}(B)$
is given by
$\mathrm {Ran}(A) = \mathrm {Ran}(B)$
is given by
![]() $\mathbb {P} = \sqrt {B}^\dagger B \sqrt {B}^\dagger = \sqrt {A}^\dagger A \sqrt {A}^\dagger$
. By
$\mathbb {P} = \sqrt {B}^\dagger B \sqrt {B}^\dagger = \sqrt {A}^\dagger A \sqrt {A}^\dagger$
. By
![]() $A - B \succeq 0$
, we have
$A - B \succeq 0$
, we have
![]() $\sqrt {B}^\dagger A \sqrt {B}^\dagger - \mathbb {P} \succeq 0$
, which means that all the eigenvalues of the matrix
$\sqrt {B}^\dagger A \sqrt {B}^\dagger - \mathbb {P} \succeq 0$
, which means that all the eigenvalues of the matrix
![]() $\sqrt {B}^\dagger A \sqrt {B}^\dagger$
restricted on its invariant subspace
$\sqrt {B}^\dagger A \sqrt {B}^\dagger$
restricted on its invariant subspace
![]() $\mathrm {Ran}(A) = \mathrm {Ran}(B)$
is greater than or equal to one. It is easy to see that
$\mathrm {Ran}(A) = \mathrm {Ran}(B)$
is greater than or equal to one. It is easy to see that
![]() $\sqrt {B}^\dagger A \sqrt {B}^\dagger$
and
$\sqrt {B}^\dagger A \sqrt {B}^\dagger$
and
![]() $\sqrt {A} B^\dagger \sqrt {A}$
have the same eigenvalues. Hence, we find
$\sqrt {A} B^\dagger \sqrt {A}$
have the same eigenvalues. Hence, we find
![]() $\sqrt {A} B^\dagger \sqrt {A} - \mathbb {P} \succeq 0$
, which gives
$\sqrt {A} B^\dagger \sqrt {A} - \mathbb {P} \succeq 0$
, which gives
![]() $B^\dagger \succeq A^\dagger$
by conjugating with
$B^\dagger \succeq A^\dagger$
by conjugating with
![]() $\sqrt {A}^\dagger$
.
$\sqrt {A}^\dagger$
.
The next lemma is about the measurability of matrix-valued functions.
Lemma 2.3.
Let
![]() $A(x)$
be a
$A(x)$
be a
![]() $\mathbb {S}^n$
-valued Borel measurable function on
$\mathbb {S}^n$
-valued Borel measurable function on
![]() $\mathcal {X}$
. Then, it holds that
$\mathcal {X}$
. Then, it holds that
-
1. The eigenvalues
 $\{\lambda _{A,i}(x)\}^n_{i = 1}$
of
$\{\lambda _{A,i}(x)\}^n_{i = 1}$
of
 $A(x)$
in nondecreasing order are measurable, and the corresponding eigenvectors
$A(x)$
in nondecreasing order are measurable, and the corresponding eigenvectors
 $\{u_{A,i}(x)\}^n_{i=1}$
can also be selected to be measurable and form an orthonormal basis of
$\{u_{A,i}(x)\}^n_{i=1}$
can also be selected to be measurable and form an orthonormal basis of
 $\mathbb {R}^n$
for every
$\mathbb {R}^n$
for every
 $x \in \mathcal {X}$
.
$x \in \mathcal {X}$
. -
2. The pseudoinverse
 $A^\dagger (x)$
of
$A^\dagger (x)$
of
 $A(x)$
is measurable, and the square root
$A(x)$
is measurable, and the square root
 $A^{1/2}(x)$
of
$A^{1/2}(x)$
of
 $A(x) \in \mathbb {S}^n_+$
is measurable.
$A(x) \in \mathbb {S}^n_+$
is measurable.
The first and second properties are from [Reference Reid81] and [Reference Robertson and Rosenberg82] with the continuity of
![]() $A^{1/2}$
in
$A^{1/2}$
in
![]() $A \in \mathbb {S}^n_+$
, respectively. In fact, Powers–Størmer inequality [Reference Powers and Størmer80] gives
$A \in \mathbb {S}^n_+$
, respectively. In fact, Powers–Størmer inequality [Reference Powers and Størmer80] gives
We finally recall some concepts and useful results from convex analysis. Let
![]() $f\,:\,X \to \mathbb {R} \cup \{+ \infty \}$
be an extended real-valued function on a Banach space
$f\,:\,X \to \mathbb {R} \cup \{+ \infty \}$
be an extended real-valued function on a Banach space
![]() $X$
. We denote by
$X$
. We denote by
![]() $\partial f(x)$
its subgradient at
$\partial f(x)$
its subgradient at
![]() $x \in X$
and by
$x \in X$
and by
![]() $dom(f) \,:\!=\, f^{-1}(\mathbb {R})$
its domain. We say that
$dom(f) \,:\!=\, f^{-1}(\mathbb {R})$
its domain. We say that
![]() $f$
is proper if
$f$
is proper if
![]() $dom(f) \neq \varnothing$
; and that
$dom(f) \neq \varnothing$
; and that
![]() $f$
is positively homogeneous of degree
$f$
is positively homogeneous of degree
![]() $k$
if for all
$k$
if for all
![]() $x \in X$
and
$x \in X$
and
![]() $\alpha \gt 0$
,
$\alpha \gt 0$
,
![]() $f(\alpha x) = \alpha ^k f(x)$
. The conjugate function
$f(\alpha x) = \alpha ^k f(x)$
. The conjugate function
![]() $f^*$
of
$f^*$
of
![]() $f$
is defined by
$f$
is defined by
which is convex and lower semicontinuous with respect to the weak* topology of
![]() $X^*$
. The following two lemmas are from [Reference Barbu and Precupanu4, Proposition 2.33] and [Reference Bouchitté12, Proposition 2.5], respectively.
$X^*$
. The following two lemmas are from [Reference Barbu and Precupanu4, Proposition 2.33] and [Reference Bouchitté12, Proposition 2.5], respectively.
Lemma 2.4 (Subgradient). Let
![]() $f\,:\,X \to \mathbb {R} \cup \{+\infty \}$
be a proper convex function on a Banach space
$f\,:\,X \to \mathbb {R} \cup \{+\infty \}$
be a proper convex function on a Banach space
![]() $X$
. Then, the following three properties are equivalent: (i)
$X$
. Then, the following three properties are equivalent: (i)
![]() $x^* \in \partial f(x)$
; (ii)
$x^* \in \partial f(x)$
; (ii)
![]() $f(x) + f^*(x^*) = \langle x^*,x\rangle _X$
; (iii)
$f(x) + f^*(x^*) = \langle x^*,x\rangle _X$
; (iii)
![]() $f(x) + f^*(x^*) \le \langle x^*,x\rangle _X$
. In addition, if
$f(x) + f^*(x^*) \le \langle x^*,x\rangle _X$
. In addition, if
![]() $f$
is lower semicontinuous, then all of these properties are equivalent to
$f$
is lower semicontinuous, then all of these properties are equivalent to
![]() $x \in \partial f^*(x^*)$
.
$x \in \partial f^*(x^*)$
.
Lemma 2.5 (Fenchel–Rockafellar duality). Let
![]() $X$
and
$X$
and
![]() $Y$
be two Banach spaces and
$Y$
be two Banach spaces and
![]() $L\,:\, X \to Y$
be a bounded linear operator with the adjoint
$L\,:\, X \to Y$
be a bounded linear operator with the adjoint
![]() $L^*\,:\, Y^* \to X^*$
. Let
$L^*\,:\, Y^* \to X^*$
. Let
![]() $f$
and
$f$
and
![]() $g$
be two proper lower semicontinuous convex functions defined on
$g$
be two proper lower semicontinuous convex functions defined on
![]() $X$
and
$X$
and
![]() $Y$
valued in
$Y$
valued in
![]() $\mathbb {R} \cup \{+\infty \}$
, respectively. If there exists
$\mathbb {R} \cup \{+\infty \}$
, respectively. If there exists
![]() $x \in dom (f)$
such that
$x \in dom (f)$
such that
![]() $g$
is continuous at
$g$
is continuous at
![]() $Lx$
, then
$Lx$
, then
and the
![]() $\inf$
in (2.7) can be attained. Moreover, the
$\inf$
in (2.7) can be attained. Moreover, the
![]() $\sup$
in (2.7) is attained at
$\sup$
in (2.7) is attained at
![]() $x \in X$
if and only if there exists a
$x \in X$
if and only if there exists a
![]() $y^* \in Y^*$
such that
$y^* \in Y^*$
such that
![]() $L x \in \partial g^*(y^*)$
and
$L x \in \partial g^*(y^*)$
and
![]() $L^* y^* \in \partial f({-}x)$
, in which case
$L^* y^* \in \partial f({-}x)$
, in which case
![]() $y^*$
also achieves the
$y^*$
also achieves the
![]() $\inf$
in (2.7).
$\inf$
in (2.7).
3. Definition and basic properties
We shall introduce a new family of distances on the matrix-valued Radon measure space
![]() $\mathcal {M}(\Omega, \mathbb {S}^n_+)$
based on a dynamic OT formulation, which will be the central object of this work.
$\mathcal {M}(\Omega, \mathbb {S}^n_+)$
based on a dynamic OT formulation, which will be the central object of this work.
3.1. Action functional
To define our dynamic OT model over the space of
![]() $\mathbb {S}^n_+$
-valued measures, the starting point is a weighted action functional. Let
$\mathbb {S}^n_+$
-valued measures, the starting point is a weighted action functional. Let
![]() $n, k, m \in \mathbb {N}$
be positive integers and
$n, k, m \in \mathbb {N}$
be positive integers and
![]() $\Lambda \,:\!=\, (\Lambda _1,\Lambda _2)$
be a pair of matrices with
$\Lambda \,:\!=\, (\Lambda _1,\Lambda _2)$
be a pair of matrices with
![]() $\Lambda _1 \in \mathbb {S}^k_+$
and
$\Lambda _1 \in \mathbb {S}^k_+$
and
![]() $\Lambda _2 \in \mathbb {S}_+^m$
. We define the following closed convex set:
$\Lambda _2 \in \mathbb {S}_+^m$
. We define the following closed convex set:
Note that its characteristic function:
 \begin{equation*} \iota _{\mathcal {O}_\Lambda } \,:\!=\, \begin{cases} 0, & (A,B,C) \in \mathcal {O}_\Lambda \,,\\ + \infty, & (A,B,C) \notin \mathcal {O}_\Lambda \,,\\ \end{cases} \end{equation*}
\begin{equation*} \iota _{\mathcal {O}_\Lambda } \,:\!=\, \begin{cases} 0, & (A,B,C) \in \mathcal {O}_\Lambda \,,\\ + \infty, & (A,B,C) \notin \mathcal {O}_\Lambda \,,\\ \end{cases} \end{equation*}
is proper lower semicontinuous and convex [Reference Bauschke and Combettes6, Lemma 1.24]. We denote by
![]() $J_\Lambda$
the conjugate function (2.6) of
$J_\Lambda$
the conjugate function (2.6) of
![]() $\iota _{\mathcal {O}_\Lambda }$
and derive the explicit expressions for
$\iota _{\mathcal {O}_\Lambda }$
and derive the explicit expressions for
![]() $J_\Lambda$
and its subgradient
$J_\Lambda$
and its subgradient
![]() $\partial J_\Lambda$
.
$\partial J_\Lambda$
.
Proposition 3.1.
![]() $J_\Lambda$
is proper, positively homogeneous of degree one, lower semicontinuous and convex with the following representation:
$J_\Lambda$
is proper, positively homogeneous of degree one, lower semicontinuous and convex with the following representation:
if
![]() $X \in \mathbb {S}_+^n$
,
$X \in \mathbb {S}_+^n$
,
![]() $\mathrm {Ran} (Y^{\mathrm {T}}) \subset \mathrm {Ran} ( \Lambda _1)$
,
$\mathrm {Ran} (Y^{\mathrm {T}}) \subset \mathrm {Ran} ( \Lambda _1)$
,
![]() $\mathrm {Ran} (Z^{\mathrm {T}}) \subset \mathrm {Ran} (\Lambda _2)$
and
$\mathrm {Ran} (Z^{\mathrm {T}}) \subset \mathrm {Ran} (\Lambda _2)$
and
![]() $\mathrm {Ran} ([Y,Z]) \subset \mathrm {Ran}(X)$
; otherwise,
$\mathrm {Ran} ([Y,Z]) \subset \mathrm {Ran}(X)$
; otherwise,
![]() $J_\Lambda (X, Y, Z) = +\infty$
. Moreover, the subgradient of
$J_\Lambda (X, Y, Z) = +\infty$
. Moreover, the subgradient of
![]() $J_\Lambda$
at
$J_\Lambda$
at
![]() $(X,Y, Z) \in dom (J_\Lambda )$
is characterised by
$(X,Y, Z) \in dom (J_\Lambda )$
is characterised by
![]() $\partial J_\Lambda (X, Y, Z)$
is a singleton if and only if
$\partial J_\Lambda (X, Y, Z)$
is a singleton if and only if
![]() $(X, Y, Z) \in \mathbb {S}^n_{++} \times \mathbb {R}^{n \times k} \times \mathbb {R}^{n \times m}$
and
$(X, Y, Z) \in \mathbb {S}^n_{++} \times \mathbb {R}^{n \times k} \times \mathbb {R}^{n \times m}$
and
![]() $\Lambda _1 \in \mathbb {S}_{++}^k$
,
$\Lambda _1 \in \mathbb {S}_{++}^k$
,
![]() $\Lambda _2 \in \mathbb {S}_{++}^m$
.
$\Lambda _2 \in \mathbb {S}_{++}^m$
.
Proof. The properties of
![]() $J_\Lambda$
are by [Reference Bauschke and Combettes6, Proposition 14.11]. To derive the formula (3.2), by definition, we have
$J_\Lambda$
are by [Reference Bauschke and Combettes6, Proposition 14.11]. To derive the formula (3.2), by definition, we have
for
![]() $(X, Y, Z) \in \mathbb {S}^n \times \mathbb {R}^{n \times k} \times \mathbb {R}^{n \times m}$
. We consider the following four cases.
$(X, Y, Z) \in \mathbb {S}^n \times \mathbb {R}^{n \times k} \times \mathbb {R}^{n \times m}$
. We consider the following four cases.
Case I:
![]() $X \in \mathbb {S}^n\backslash \mathbb {S}_+^n$
. We choose a vector
$X \in \mathbb {S}^n\backslash \mathbb {S}_+^n$
. We choose a vector
![]() $a \in \mathbb {R}^n$
such that
$a \in \mathbb {R}^n$
such that
![]() $\langle a, X a \rangle \lt 0$
and set
$\langle a, X a \rangle \lt 0$
and set
![]() $A = - \lambda a a^{\mathrm {T}}\preceq 0$
with
$A = - \lambda a a^{\mathrm {T}}\preceq 0$
with
![]() $\lambda \gt 0$
,
$\lambda \gt 0$
,
![]() $B = 0$
and
$B = 0$
and
![]() $C = 0$
in (3.4). Then it follows that
$C = 0$
in (3.4). Then it follows that
Case II:
![]() $\mathrm {Ran} (Y^{\mathrm {T}}) \not \subset \mathrm {Ran} (\Lambda _1)$
or
$\mathrm {Ran} (Y^{\mathrm {T}}) \not \subset \mathrm {Ran} (\Lambda _1)$
or
![]() $\mathrm {Ran} (Z^{\mathrm {T}}) \not \subset \mathrm {Ran} (\Lambda _2)$
. It suffices to consider the case
$\mathrm {Ran} (Z^{\mathrm {T}}) \not \subset \mathrm {Ran} (\Lambda _2)$
. It suffices to consider the case
![]() $\mathrm {Ran} (Y^{\mathrm {T}}) \not \subset \mathrm {Ran} (\Lambda _1)$
, since the same argument applies to the other one. Without loss of generality, we let
$\mathrm {Ran} (Y^{\mathrm {T}}) \not \subset \mathrm {Ran} (\Lambda _1)$
, since the same argument applies to the other one. Without loss of generality, we let
![]() $Y = [y_1,\ldots, y_n]^{\mathrm {T}}$
with
$Y = [y_1,\ldots, y_n]^{\mathrm {T}}$
with
![]() $y_i \in \mathbb {R}^k$
and
$y_i \in \mathbb {R}^k$
and
![]() $y_1 \notin \mathrm {Ran} (\Lambda _1)$
. Thanks to
$y_1 \notin \mathrm {Ran} (\Lambda _1)$
. Thanks to
![]() $\Lambda _1 \in \mathbb {S}^k_+$
,
$\Lambda _1 \in \mathbb {S}^k_+$
,
![]() $y_1$
has the orthogonal decomposition:
$y_1$
has the orthogonal decomposition:
Taking
![]() $A = 0$
,
$A = 0$
,
![]() $B = \lambda \big [y_1^{(2)},0\big ]^{\mathrm {T}}$
with
$B = \lambda \big [y_1^{(2)},0\big ]^{\mathrm {T}}$
with
![]() $\lambda \in \mathbb {R}$
and
$\lambda \in \mathbb {R}$
and
![]() $C = 0$
in (3.4), we have
$C = 0$
in (3.4), we have
Case III:
![]() $\mathrm {Ran} ([Y, Z]) \not \subset \mathrm {Ran}(X)$
. It suffices to consider
$\mathrm {Ran} ([Y, Z]) \not \subset \mathrm {Ran}(X)$
. It suffices to consider
![]() $\mathrm {Ran}( Y ) \not \subset \mathrm {Ran} (X)$
. We take
$\mathrm {Ran}( Y ) \not \subset \mathrm {Ran} (X)$
. We take
![]() $(A,B,C)$
in (3.4) as:
$(A,B,C)$
in (3.4) as:
with
![]() $\lambda \gt 0$
, where
$\lambda \gt 0$
, where
![]() $\mathbb {P}_{\mathrm {Ker}(X)}\,:\!=\, I - X^\dagger X$
is the orthogonal projection onto
$\mathbb {P}_{\mathrm {Ker}(X)}\,:\!=\, I - X^\dagger X$
is the orthogonal projection onto
![]() $\mathrm {Ker}(X)$
. A direct computation gives
$\mathrm {Ker}(X)$
. A direct computation gives
 \begin{align*} J_\Lambda (X,Y, Z) &\ge \sup _{(A,B,0) \in \mathcal {O}_\Lambda } X \cdot A + Y \cdot B \\ & \ge \sup _{\lambda \gt 0} - \frac { \lambda ^2}{2} (\mathbb {P}_{\mathrm {Ker}(X)} Y \Lambda _1)\cdot (X \mathbb {P}_{\mathrm {Ker}(X)} Y \Lambda _1) + \lambda Y \cdot ( \mathbb {P}_{\mathrm {Ker}(X)} Y) \\ & \ge \sup _{\lambda \gt 0} \lambda (\mathbb {P}_{\mathrm {Ker}(X)} Y) \cdot (\mathbb {P}_{\mathrm {Ker}(X)} Y) = + \infty \,, \end{align*}
\begin{align*} J_\Lambda (X,Y, Z) &\ge \sup _{(A,B,0) \in \mathcal {O}_\Lambda } X \cdot A + Y \cdot B \\ & \ge \sup _{\lambda \gt 0} - \frac { \lambda ^2}{2} (\mathbb {P}_{\mathrm {Ker}(X)} Y \Lambda _1)\cdot (X \mathbb {P}_{\mathrm {Ker}(X)} Y \Lambda _1) + \lambda Y \cdot ( \mathbb {P}_{\mathrm {Ker}(X)} Y) \\ & \ge \sup _{\lambda \gt 0} \lambda (\mathbb {P}_{\mathrm {Ker}(X)} Y) \cdot (\mathbb {P}_{\mathrm {Ker}(X)} Y) = + \infty \,, \end{align*}
since there holds
![]() $( \mathbb {P}_{\mathrm {Ker}(X)} Y) \cdot (\mathbb {P}_{\mathrm {Ker}(X)} Y) \gt 0$
by
$( \mathbb {P}_{\mathrm {Ker}(X)} Y) \cdot (\mathbb {P}_{\mathrm {Ker}(X)} Y) \gt 0$
by
![]() $\mathrm {Ran}( Y ) \not \subset \mathrm {Ran} (X)$
.
$\mathrm {Ran}( Y ) \not \subset \mathrm {Ran} (X)$
.
Case IV:
![]() $(X, Y,Z) \in \mathbb {S}_+^{n} \times \mathbb {R}^{n \times k} \times \mathbb {R}^{n \times m}$
with
$(X, Y,Z) \in \mathbb {S}_+^{n} \times \mathbb {R}^{n \times k} \times \mathbb {R}^{n \times m}$
with
![]() $\mathrm {Ran} (Y^{\mathrm {T}}) \subset \mathrm {Ran} (\Lambda _1)$
,
$\mathrm {Ran} (Y^{\mathrm {T}}) \subset \mathrm {Ran} (\Lambda _1)$
,
![]() $\mathrm {Ran} (Z^{\mathrm {T}}) \subset \mathrm {Ran} (\Lambda _2)$
and
$\mathrm {Ran} (Z^{\mathrm {T}}) \subset \mathrm {Ran} (\Lambda _2)$
and
![]() $\mathrm {Ran} ([Y, Z]) \subset \mathrm {Ran}(X)$
. For this case, we directly compute
$\mathrm {Ran} ([Y, Z]) \subset \mathrm {Ran}(X)$
. For this case, we directly compute
and
 \begin{align} Y \cdot B + Z \cdot C - \frac {1}{2} X \cdot \big (B \Lambda _1^2 B^{\mathrm {T}} + C \Lambda ^2_2 C^{\mathrm {T}} \big ) = & - \frac {1}{2} \Big \lVert \sqrt {X}B \Lambda _1 - \sqrt {X}^{\dagger } Y \Lambda _1^\dagger \Big \lVert _{\mathrm {F}}^2 - \frac {1}{2} \Big \lVert \sqrt {X}C \Lambda _2 - \sqrt {X}^{\dagger } Z \Lambda _2^\dagger \Big \lVert _{\mathrm {F}}^2 \notag \\ & + \frac {1}{2 } \Big \lVert \sqrt {X}^{\dagger } Y \Lambda _1^\dagger \Big \lVert _{\mathrm {F}}^2 + \frac {1}{2} \Big \lVert \sqrt {X}^{\dagger } Z \Lambda _2^\dagger \Big \lVert _{\mathrm {F}}^2\,, \end{align}
\begin{align} Y \cdot B + Z \cdot C - \frac {1}{2} X \cdot \big (B \Lambda _1^2 B^{\mathrm {T}} + C \Lambda ^2_2 C^{\mathrm {T}} \big ) = & - \frac {1}{2} \Big \lVert \sqrt {X}B \Lambda _1 - \sqrt {X}^{\dagger } Y \Lambda _1^\dagger \Big \lVert _{\mathrm {F}}^2 - \frac {1}{2} \Big \lVert \sqrt {X}C \Lambda _2 - \sqrt {X}^{\dagger } Z \Lambda _2^\dagger \Big \lVert _{\mathrm {F}}^2 \notag \\ & + \frac {1}{2 } \Big \lVert \sqrt {X}^{\dagger } Y \Lambda _1^\dagger \Big \lVert _{\mathrm {F}}^2 + \frac {1}{2} \Big \lVert \sqrt {X}^{\dagger } Z \Lambda _2^\dagger \Big \lVert _{\mathrm {F}}^2\,, \end{align}
where we have used
by the range relations:
![]() $\mathrm {Ran} (Y^{\mathrm {T}}) \subset \mathrm {Ran} (\Lambda _1)$
,
$\mathrm {Ran} (Y^{\mathrm {T}}) \subset \mathrm {Ran} (\Lambda _1)$
,
![]() $\mathrm {Ran} (Z^{\mathrm {T}}) \subset \mathrm {Ran} (\Lambda _2)$
and
$\mathrm {Ran} (Z^{\mathrm {T}}) \subset \mathrm {Ran} (\Lambda _2)$
and
![]() $\mathrm {Ran} ([Y,Z]) \subset \mathrm {Ran}(X)$
. Also, by (3.1), we have
$\mathrm {Ran} ([Y,Z]) \subset \mathrm {Ran}(X)$
. Also, by (3.1), we have
![]() $ X \cdot \big (A + \frac {1}{2} B \Lambda _1^2 B^{\mathrm {T}} + \frac {1}{2} C \Lambda _2^2 C^{\mathrm {T}} \big ) \le 0$
. Hence, by (3.5) and (3.6), the maximisers to (3.4) are given by the set
$ X \cdot \big (A + \frac {1}{2} B \Lambda _1^2 B^{\mathrm {T}} + \frac {1}{2} C \Lambda _2^2 C^{\mathrm {T}} \big ) \le 0$
. Hence, by (3.5) and (3.6), the maximisers to (3.4) are given by the set
and the corresponding supremum is (3.2).
Finally, to characterise the subgradient of
![]() $J_\Lambda$
, by Lemma2.4, we have that
$J_\Lambda$
, by Lemma2.4, we have that
![]() $(A,B,C) \in \partial J_\Lambda (X,Y,Z)$
if and only if
$(A,B,C) \in \partial J_\Lambda (X,Y,Z)$
if and only if
![]() $(A,B,C) \in \mathcal {O}_\Lambda$
and
$(A,B,C) \in \mathcal {O}_\Lambda$
and
![]() $ J_\Lambda (X,Y,Z) = X \cdot A + Y \cdot B + Z \cdot C$
holds. Then, (3.3) readily follows from the above argument. For the last statement, we note that
$ J_\Lambda (X,Y,Z) = X \cdot A + Y \cdot B + Z \cdot C$
holds. Then, (3.3) readily follows from the above argument. For the last statement, we note that
![]() $\partial J_\Lambda (X,Y,Z)$
is a singleton if and only if the equations in (3.3) for
$\partial J_\Lambda (X,Y,Z)$
is a singleton if and only if the equations in (3.3) for
![]() $(A,B,C)$
are uniquely solvable, which is equivalent to
$(A,B,C)$
are uniquely solvable, which is equivalent to
![]() $\Lambda _1 \in \mathbb {S}_{++}^k$
,
$\Lambda _1 \in \mathbb {S}_{++}^k$
,
![]() $\Lambda _2 \in \mathbb {S}_{++}^m$
and
$\Lambda _2 \in \mathbb {S}_{++}^m$
and
![]() $X \in \mathbb {S}_{++}^n$
.
$X \in \mathbb {S}_{++}^n$
.
Similarly to the unbalanced WFR distance [Reference Chizat, Peyré, Schmitzer and Vialard27, Reference Kondratyev, Monsaingeon and Vorotnikov56, Reference Liero, Mielke and Savaré64], the variables
![]() $(X, Y, Z) \in \mathbb {S}^n \times \mathbb {R}^{n \times k} \times \mathbb {R}^{n \times m}$
in the infinitesimal cost
$(X, Y, Z) \in \mathbb {S}^n \times \mathbb {R}^{n \times k} \times \mathbb {R}^{n \times m}$
in the infinitesimal cost
![]() $J_\Lambda (X, Y, Z)$
represent the mass, the momentum for the mass transportation and the source for the mass variation, respectively, in our transport problem (see Remark3.6 and Definition3.8). In what follows, we assume
$J_\Lambda (X, Y, Z)$
represent the mass, the momentum for the mass transportation and the source for the mass variation, respectively, in our transport problem (see Remark3.6 and Definition3.8). In what follows, we assume
![]() $m = n$
, since the dimensions of the mass
$m = n$
, since the dimensions of the mass
![]() $X \in \mathbb {S}^n$
and the source
$X \in \mathbb {S}^n$
and the source
![]() $Z \in \mathbb {R}^{n \times m}$
need to match. We shall also let
$Z \in \mathbb {R}^{n \times m}$
need to match. We shall also let
![]() $\Lambda _2 \in \mathbb {S}^n_{++}$
to avoid technical issues (see Remark3.10). Now, for a given triplet of measures
$\Lambda _2 \in \mathbb {S}^n_{++}$
to avoid technical issues (see Remark3.10). Now, for a given triplet of measures
![]() $\mu \,:\!=\, \mathsf {(G,q, R)} \in \mathcal {M}(\mathcal {X}, \mathbb {S}^n \times \mathbb {R}^{n \times k} \times \mathbb {M}^n)$
, we define a positive measure
$\mu \,:\!=\, \mathsf {(G,q, R)} \in \mathcal {M}(\mathcal {X}, \mathbb {S}^n \times \mathbb {R}^{n \times k} \times \mathbb {M}^n)$
, we define a positive measure
![]() $\mathcal {J}_{\Lambda } (\mu )$
on
$\mathcal {J}_{\Lambda } (\mu )$
on
![]() $\mathcal {X}$
by
$\mathcal {X}$
by
for a measurable set
![]() $E \in \mathscr {B}(\mathcal {X})$
, where
$E \in \mathscr {B}(\mathcal {X})$
, where
![]() $\lambda \in \mathcal {M}(\mathcal {X},\mathbb {R}_+)$
is a reference measure such that
$\lambda \in \mathcal {M}(\mathcal {X},\mathbb {R}_+)$
is a reference measure such that
![]() $|\mu | \ll \lambda$
. Thanks to the positive homogeneity of
$|\mu | \ll \lambda$
. Thanks to the positive homogeneity of
![]() $J_\Lambda$
by Proposition3.1, the definition (3.8) of
$J_\Lambda$
by Proposition3.1, the definition (3.8) of
![]() $\mathcal {J}_{\Lambda }$
is independent of the choice of
$\mathcal {J}_{\Lambda }$
is independent of the choice of
![]() $\lambda$
. To alleviate notations, we adopt the following conventions in the rest of this work.
$\lambda$
. To alleviate notations, we adopt the following conventions in the rest of this work.
-
• We define the space
 $\mathbb {X} \,:\!=\, \mathbb {S}^n \times \mathbb {R}^{n \times k} \times \mathbb {M}^n$
and then write
$\mathbb {X} \,:\!=\, \mathbb {S}^n \times \mathbb {R}^{n \times k} \times \mathbb {M}^n$
and then write
 $\mathcal {M}(\mathcal {X},\mathbb {X}) = \mathcal {M}(\mathcal {X}, \mathbb {S}^n \times \mathbb {R}^{n \times k} \times \mathbb {M}^n) = C(\mathcal {X},\mathbb {X})^*$
, where
$\mathcal {M}(\mathcal {X},\mathbb {X}) = \mathcal {M}(\mathcal {X}, \mathbb {S}^n \times \mathbb {R}^{n \times k} \times \mathbb {M}^n) = C(\mathcal {X},\mathbb {X})^*$
, where
 $C(\mathcal {X},\mathbb {X}) = C(\mathcal {X}, \mathbb {S}^n \times \mathbb {R}^{n \times k} \times \mathbb {M}^n)$
.
$C(\mathcal {X},\mathbb {X}) = C(\mathcal {X}, \mathbb {S}^n \times \mathbb {R}^{n \times k} \times \mathbb {M}^n)$
. -
• We often write
 $\mu$
for
$\mu$
for
 $\mathsf {(G,q,R)} \in \mathcal {M}(\mathcal {X},\mathbb {X})$
for short, which will be clear from the context.
$\mathsf {(G,q,R)} \in \mathcal {M}(\mathcal {X},\mathbb {X})$
for short, which will be clear from the context. -
• We write
 $\mathcal {J}_{\Lambda }(\mu )(E)$
as
$\mathcal {J}_{\Lambda }(\mu )(E)$
as
 $\mathcal {J}_{\Lambda, E}(\mu )$
for short. Then,
$\mathcal {J}_{\Lambda, E}(\mu )$
for short. Then,
 $\mathcal {J}_{\Lambda, \mathcal {X}}(\mu )$
denotes the total measure
$\mathcal {J}_{\Lambda, \mathcal {X}}(\mu )$
denotes the total measure
 $\mathcal {J}_{\Lambda }(\mu )(\mathcal {X})$
.
$\mathcal {J}_{\Lambda }(\mu )(\mathcal {X})$
. -
• We denote by
 $(G_\lambda, q_\lambda, R_\lambda )$
the density of
$(G_\lambda, q_\lambda, R_\lambda )$
the density of
 $\mathsf {(G,q,R)} \in \mathcal {M}(\mathcal {X},\mathbb {X})$
with respect to a reference measure
$\mathsf {(G,q,R)} \in \mathcal {M}(\mathcal {X},\mathbb {X})$
with respect to a reference measure
 $\lambda \in \mathcal {M}(\mathcal {X},\mathbb {R}_+)$
such that
$\lambda \in \mathcal {M}(\mathcal {X},\mathbb {R}_+)$
such that
 $|\mathsf {(G,q,R)}| \ll \lambda$
. The subscript
$|\mathsf {(G,q,R)}| \ll \lambda$
. The subscript
 $\lambda$
of
$\lambda$
of
 $(G_\lambda, q_\lambda, R_\lambda )$
will often be omitted for simplicity.
$(G_\lambda, q_\lambda, R_\lambda )$
will often be omitted for simplicity. -
• The generic positive constant
 $C$
involved in the estimates below may change from line to line.
$C$
involved in the estimates below may change from line to line.
Definition 3.2.
We define the
![]() $\Lambda$
-weighted action functional for a measure
$\Lambda$
-weighted action functional for a measure
![]() $\mu \in \mathcal {M}(\mathcal {X}, \mathbb {X})$
by
$\mu \in \mathcal {M}(\mathcal {X}, \mathbb {X})$
by
![]() $\mathcal {J}_{\Lambda, \mathcal {X}}(\mu )$
.
$\mathcal {J}_{\Lambda, \mathcal {X}}(\mu )$
.
By Proposition3.1 and the formula (3.8), we have the following useful lemma.
Lemma 3.3.
For
![]() $\mu = \mathsf {(G,q,R)} \in \mathcal {M}(\mathcal {X},\mathbb {X})$
with
$\mu = \mathsf {(G,q,R)} \in \mathcal {M}(\mathcal {X},\mathbb {X})$
with
![]() $\mathcal {J}_{\Lambda, \mathcal {X}}(\mu ) \lt + \infty$
, we have
$\mathcal {J}_{\Lambda, \mathcal {X}}(\mu ) \lt + \infty$
, we have
![]() $\mathsf {G} \in \mathcal {M}(\mathcal {X},\mathbb {S}_+^n)$
and
$\mathsf {G} \in \mathcal {M}(\mathcal {X},\mathbb {S}_+^n)$
and
![]() $|(\mathsf {q}, \mathsf {R})| \ll Tr \mathsf {G}$
with
$|(\mathsf {q}, \mathsf {R})| \ll Tr \mathsf {G}$
with
Proof. By
![]() $\mathcal {J}_{\Lambda, \mathcal {X}}(\mu ) = \int _{\mathcal {X}} J_\Lambda (\mu _\lambda )\, \mathrm {d} \lambda \lt + \infty$
,
$\mathcal {J}_{\Lambda, \mathcal {X}}(\mu ) = \int _{\mathcal {X}} J_\Lambda (\mu _\lambda )\, \mathrm {d} \lambda \lt + \infty$
,
![]() $J_\Lambda (\mu _\lambda )$
is finite for
$J_\Lambda (\mu _\lambda )$
is finite for
![]() $\lambda$
-a.e.
$\lambda$
-a.e.
![]() $x \in \mathcal {X}$
, where
$x \in \mathcal {X}$
, where
![]() $\mu _\lambda = (G_\lambda, q_\lambda, R_\lambda )$
. It means that
$\mu _\lambda = (G_\lambda, q_\lambda, R_\lambda )$
. It means that
![]() $\mu _\lambda (x) \in dom(J_{\Lambda })$
holds
$\mu _\lambda (x) \in dom(J_{\Lambda })$
holds
![]() $\lambda$
-a.e., which immediately gives (3.9) by Proposition3.1. We next show the absolute continuity of
$\lambda$
-a.e., which immediately gives (3.9) by Proposition3.1. We next show the absolute continuity of
![]() $|\mathsf {q}|$
and
$|\mathsf {q}|$
and
![]() $|\mathsf {R}|$
with respect to
$|\mathsf {R}|$
with respect to
![]() $Tr \mathsf {G}$
, that is, for
$Tr \mathsf {G}$
, that is, for
![]() $E \in \mathscr {B}(\mathcal {X})$
with
$E \in \mathscr {B}(\mathcal {X})$
with
![]() $Tr \mathsf {G} (E) = 0$
, we have
$Tr \mathsf {G} (E) = 0$
, we have
![]() $|\mathsf {q}|(E) = |\mathsf {R}|(E) = 0$
. For this, we consider two measurable subsets
$|\mathsf {q}|(E) = |\mathsf {R}|(E) = 0$
. For this, we consider two measurable subsets
![]() $E_1$
and
$E_1$
and
![]() $E_2$
of
$E_2$
of
![]() $E$
with
$E$
with
![]() $E = E_1 \cup E_2$
:
$E = E_1 \cup E_2$
:
By
![]() $Tr \mathsf {G}(E_1) = 0$
and
$Tr \mathsf {G}(E_1) = 0$
and
![]() $Tr G_\lambda \gt 0$
on
$Tr G_\lambda \gt 0$
on
![]() $E_1$
everywhere, we have
$E_1$
everywhere, we have
![]() $\lambda (E_1) = 0$
. Then
$\lambda (E_1) = 0$
. Then
![]() $|\mathsf {q}|(E_1) = 0$
and
$|\mathsf {q}|(E_1) = 0$
and
![]() $|\mathsf {R}|(E_1) = 0$
follows from
$|\mathsf {R}|(E_1) = 0$
follows from
![]() $|\mathsf {q}|, |\mathsf {R}| \ll \lambda$
. Moreover, by (3.9) and
$|\mathsf {q}|, |\mathsf {R}| \ll \lambda$
. Moreover, by (3.9) and
![]() $G_\lambda = 0$
on
$G_\lambda = 0$
on
![]() $E_2$
, we have
$E_2$
, we have
![]() $q_\lambda (x) = 0$
and
$q_\lambda (x) = 0$
and
![]() $R_\lambda (x) = 0$
for
$R_\lambda (x) = 0$
for
![]() $\lambda$
-a.e.
$\lambda$
-a.e.
![]() $x \in E_2$
. Then it follows that
$x \in E_2$
. Then it follows that
![]() $|\mathsf {q}|(E_2) = 0$
and
$|\mathsf {q}|(E_2) = 0$
and
![]() $|\mathsf {R}|(E_2) = 0$
. The proof is complete.
$|\mathsf {R}|(E_2) = 0$
. The proof is complete.
3.2. Continuity equation
Another key ingredient for the dynamic OT formulation is a matricial continuity equation; see Definition3.4 below. Let us fix more notations.
-
• Let
 $\Omega \subset \mathbb {R}^d$
be a compact set with a nonempty interior, a smooth boundary
$\Omega \subset \mathbb {R}^d$
be a compact set with a nonempty interior, a smooth boundary
 $\partial \Omega$
and the exterior unit normal vector
$\partial \Omega$
and the exterior unit normal vector
 $\nu = (\nu _1,\ldots, \nu _d)$
. We denote by
$\nu = (\nu _1,\ldots, \nu _d)$
. We denote by
 $Q_a^b \,:\!=\, [a,b] \times \Omega \subset \mathbb {R}^{1 + d}$
with
$Q_a^b \,:\!=\, [a,b] \times \Omega \subset \mathbb {R}^{1 + d}$
with
 $b \gt a \gt 0$
the associated time-space domain. If
$b \gt a \gt 0$
the associated time-space domain. If
 $[a,b] = [0,1]$
, we simply write it as
$[a,b] = [0,1]$
, we simply write it as
 $Q$
.
$Q$
. -
• For a function
 $\Phi (t,x)$
on
$\Phi (t,x)$
on
 $Q_a^b$
, we write
$Q_a^b$
, we write
 $\Phi _t(\cdot ) \,:\!=\, \Phi (t,\cdot )$
if we regard it as a family of functions
$\Phi _t(\cdot ) \,:\!=\, \Phi (t,\cdot )$
if we regard it as a family of functions
 $\{\Phi _t\}_{t \in [a,b]}$
in
$\{\Phi _t\}_{t \in [a,b]}$
in
 $x$
.
$x$
. -
• We denote by
 $\pi ^t\,:\, (t,x) \to t$
the projection. We use the subscript
$\pi ^t\,:\, (t,x) \to t$
the projection. We use the subscript
 $\#$
to denote the pushforward by a map. For instance, for a measure
$\#$
to denote the pushforward by a map. For instance, for a measure
 $\mu$
on
$\mu$
on
 $Q_a^b$
,
$Q_a^b$
,
 $\pi ^t_\# \mu = \mu \circ (\pi ^t)^{-1}$
is the pushforward measure on
$\pi ^t_\# \mu = \mu \circ (\pi ^t)^{-1}$
is the pushforward measure on
 $[a,b]$
.
$[a,b]$
. -
• Let
 $X$
and
$X$
and
 $Y$
be two Banach spaces. We denote by
$Y$
be two Banach spaces. We denote by
 $\mathcal {L}(X,Y)$
the space of continuous linear operators from
$\mathcal {L}(X,Y)$
the space of continuous linear operators from
 $X$
to
$X$
to
 $Y$
(simply
$Y$
(simply
 $\mathcal {L}(X)$
if
$\mathcal {L}(X)$
if
 $X = Y$
) and by
$X = Y$
) and by
 $C_c^\infty (\mathbb {R}^d,X)$
the
$C_c^\infty (\mathbb {R}^d,X)$
the
 $X$
-valued smooth functions with compact support. We also need
$X$
-valued smooth functions with compact support. We also need
 $C^k$
-smooth functions
$C^k$
-smooth functions
 $C^k(\Omega, X)$
, where we assume that the derivatives exist in the interior of
$C^k(\Omega, X)$
, where we assume that the derivatives exist in the interior of
 $\Omega$
and can be continuously extended to the boundary. The norm on
$\Omega$
and can be continuously extended to the boundary. The norm on
 $C^k(\Omega, X)$
is defined by
$C^k(\Omega, X)$
is defined by
 $\lVert \Phi \rVert _{k,\infty } \,:\!=\, \sum _{|\alpha | \le k} \sup _{x \in \Omega } \lVert D^\alpha \Phi (x) \rVert$
. Other similar notations are interpreted accordingly.
$\lVert \Phi \rVert _{k,\infty } \,:\!=\, \sum _{|\alpha | \le k} \sup _{x \in \Omega } \lVert D^\alpha \Phi (x) \rVert$
. Other similar notations are interpreted accordingly. -
• We recall the indicator function of a set
 $A$
:(3.10)
$A$
:(3.10) \begin{equation} \chi _A(x) = \begin{cases} 1, & \text {if}\ x \in A\,,\\ 0, & \text {if}\ x \notin A\,. \end{cases} \end{equation}
\begin{equation} \chi _A(x) = \begin{cases} 1, & \text {if}\ x \in A\,,\\ 0, & \text {if}\ x \notin A\,. \end{cases} \end{equation}
-
• We use
 $\widehat{\cdot}$
to denote the Fourier transform of a function, or the symbol of a constant coefficient linear differential operator.
$\widehat{\cdot}$
to denote the Fourier transform of a function, or the symbol of a constant coefficient linear differential operator.
Let
![]() $\mathsf {D}^*\,:\,C_c^\infty (\mathbb {R}^d, \mathbb {S}^n) \to C_c^\infty (\mathbb {R}^d, \mathbb {R}^{n \times k})$
be a general first-order constant coefficient linear differential operator satisfying
$\mathsf {D}^*\,:\,C_c^\infty (\mathbb {R}^d, \mathbb {S}^n) \to C_c^\infty (\mathbb {R}^d, \mathbb {R}^{n \times k})$
be a general first-order constant coefficient linear differential operator satisfying
![]() $\mathsf {D}^*(I) = 0$
. That is, for a matrix-valued function
$\mathsf {D}^*(I) = 0$
. That is, for a matrix-valued function
![]() $\Phi \in C_c^\infty (\mathbb {R}^d, \mathbb {S}^n)$
with components
$\Phi \in C_c^\infty (\mathbb {R}^d, \mathbb {S}^n)$
with components
![]() $\{\Phi _{ij}\}_{i,j = 1}^n$
, we have
$\{\Phi _{ij}\}_{i,j = 1}^n$
, we have
for some matrices
![]() $\{A_l^{ij}\}_{l = 0}^d \subset \mathbb {R}^{n \times k}$
, and there holds
$\{A_l^{ij}\}_{l = 0}^d \subset \mathbb {R}^{n \times k}$
, and there holds
![]() $\sum _{i = 1}^n A_0^{ii} = 0$
. Here
$\sum _{i = 1}^n A_0^{ii} = 0$
. Here
![]() $e_{ij}$
is the
$e_{ij}$
is the
![]() $n \times n$
matrix unit with
$n \times n$
matrix unit with
![]() $1$
at the
$1$
at the
![]() $(i,j)$
-entry. By Fourier transform, the operator
$(i,j)$
-entry. By Fourier transform, the operator
![]() $\mathsf {D}^*$
can be equivalently characterised by
$\mathsf {D}^*$
can be equivalently characterised by
where
![]() $\widehat {\Phi }(\xi )$
is the Fourier transform of
$\widehat {\Phi }(\xi )$
is the Fourier transform of
![]() $\Phi$
:
$\Phi$
:
and
![]() $\widehat {\mathsf {D}^*}(\xi )\,:\, \mathbb {R}^d \to \mathcal {L}(\mathbb {S}^n,\mathbb {R}^{n \times k})$
is the symbol of
$\widehat {\mathsf {D}^*}(\xi )\,:\, \mathbb {R}^d \to \mathcal {L}(\mathbb {S}^n,\mathbb {R}^{n \times k})$
is the symbol of
![]() $\mathsf {D}^*$
such that for any
$\mathsf {D}^*$
such that for any
![]() $X \in \mathbb {S}^n$
and
$X \in \mathbb {S}^n$
and
![]() $Y \in \mathbb {R}^{n \times k}$
,
$Y \in \mathbb {R}^{n \times k}$
,
![]() $Y \cdot \widehat {\mathsf {D}^*}(\xi )[X]$
is a first-order polynomial in
$Y \cdot \widehat {\mathsf {D}^*}(\xi )[X]$
is a first-order polynomial in
![]() $\xi$
. We write
$\xi$
. We write
![]() $\widehat {\mathsf {D}^*}(\xi )$
as the sum of its homogeneous components:
$\widehat {\mathsf {D}^*}(\xi )$
as the sum of its homogeneous components:
![]() $\widehat {\mathsf {D}^*}(\xi ) = \widehat {\mathsf {D}^*_0} + \widehat {\mathsf {D}^*_1}(\xi )$
, where
$\widehat {\mathsf {D}^*}(\xi ) = \widehat {\mathsf {D}^*_0} + \widehat {\mathsf {D}^*_1}(\xi )$
, where
![]() $\widehat {\mathsf {D}^*_0}$
and
$\widehat {\mathsf {D}^*_0}$
and
![]() $\widehat {\mathsf {D}^*_1}(\xi )$
are homogeneous of degree
$\widehat {\mathsf {D}^*_1}(\xi )$
are homogeneous of degree
![]() $0$
and
$0$
and
![]() $1$
, respectively: for
$1$
, respectively: for
![]() $X = (X_{ij}) \in \mathbb {S}^n$
,
$X = (X_{ij}) \in \mathbb {S}^n$
,
and
 \begin{equation*} \widehat {\mathsf {D}^*_1}(\xi )[X] = \frac {\mathrm {i}}{2} \sum _{l = 1}^d\sum _{i = 1}^n A_l^{ii} \xi _l X_{ii} + \mathrm {i} \sum _{l = 1}^d\sum _{i \lt j} A_l^{ij} \xi _l X_{ij}\,, \end{equation*}
\begin{equation*} \widehat {\mathsf {D}^*_1}(\xi )[X] = \frac {\mathrm {i}}{2} \sum _{l = 1}^d\sum _{i = 1}^n A_l^{ii} \xi _l X_{ii} + \mathrm {i} \sum _{l = 1}^d\sum _{i \lt j} A_l^{ij} \xi _l X_{ij}\,, \end{equation*}
with matrices
![]() $A_{l}^{ij}$
given in (3.11). Then, noting that the Fourier transform of
$A_{l}^{ij}$
given in (3.11). Then, noting that the Fourier transform of
![]() $I$
is
$I$
is
![]() $\delta _0 I$
, it is easy to see that the condition
$\delta _0 I$
, it is easy to see that the condition
![]() $\mathsf {D}^*(I) = 0$
is equivalent to
$\mathsf {D}^*(I) = 0$
is equivalent to
![]() $\widehat {\mathsf {D}^*}(0)(I) = \widehat {\mathsf {D}_0^*}(I) = \frac {1}{2} \sum _{i = 1}^n A_0^{ii} = 0$
.
$\widehat {\mathsf {D}^*}(0)(I) = \widehat {\mathsf {D}_0^*}(I) = \frac {1}{2} \sum _{i = 1}^n A_0^{ii} = 0$
.
By abuse of notation, we define
![]() $\mathsf {D}^*\Phi$
for functions
$\mathsf {D}^*\Phi$
for functions
![]() $\Phi (t,x)$
on
$\Phi (t,x)$
on
![]() $\mathbb {R}^{1 + d}$
by acting
$\mathbb {R}^{1 + d}$
by acting
![]() $\mathsf {D}^*$
on the spatial variable
$\mathsf {D}^*$
on the spatial variable
![]() $x$
. Moreover, we define the operator
$x$
. Moreover, we define the operator
![]() $\mathsf {D}$
as the adjoint operator of
$\mathsf {D}$
as the adjoint operator of
![]() $ - \mathsf {D}^*$
in the sense of distribution, which can be viewed as a bdivergence operator that maps the momentum to the mass (see equation (3.14)). We similarly denote by
$ - \mathsf {D}^*$
in the sense of distribution, which can be viewed as a bdivergence operator that maps the momentum to the mass (see equation (3.14)). We similarly denote by
![]() $\mathsf {D}_0$
and
$\mathsf {D}_0$
and
![]() $\mathsf {D}_1$
the homogeneous parts of degree
$\mathsf {D}_1$
the homogeneous parts of degree
![]() $0$
and
$0$
and
![]() $1$
of the operator
$1$
of the operator
![]() $\mathsf {D}$
, respectively.
$\mathsf {D}$
, respectively.
Example 3.1.
A simple example of
![]() $\mathsf {D}$
is the entry-wise transport, in which case the mass transportation between components is forbidden. To be precise, for
$\mathsf {D}$
is the entry-wise transport, in which case the mass transportation between components is forbidden. To be precise, for
![]() $\mathsf {q} \in \mathcal {M}(Q, \mathbb {R}^{n \times n \times d})$
, we regard
$\mathsf {q} \in \mathcal {M}(Q, \mathbb {R}^{n \times n \times d})$
, we regard
![]() $\mathsf {q}$
as a collection of
$\mathsf {q}$
as a collection of
![]() $\mathbb {R}^d$
-valued measures
$\mathbb {R}^d$
-valued measures
![]() $\{\mathsf {q}_{ij}\}_{i,j =1}^n \subset \mathcal {M}(Q, \mathbb {R}^{d})$
, and define
$\{\mathsf {q}_{ij}\}_{i,j =1}^n \subset \mathcal {M}(Q, \mathbb {R}^{d})$
, and define
where the standard divergence is applied to each
![]() $q_{ij}$
, i.e.,
$q_{ij}$
, i.e.,
![]() $(\mathrm {div} \mathsf {q})_{ij} \,:\!=\, \mathrm {div} q_{ij}$
. Then, the adjoint
$(\mathrm {div} \mathsf {q})_{ij} \,:\!=\, \mathrm {div} q_{ij}$
. Then, the adjoint
![]() $\mathsf {D}^*$
is simply given by the gradient that acts on
$\mathsf {D}^*$
is simply given by the gradient that acts on
![]() $\Phi \in C_c^\infty (\mathbb {R}^d, \mathbb {S}^n)$
component-wisely:
$\Phi \in C_c^\infty (\mathbb {R}^d, \mathbb {S}^n)$
component-wisely:
![]() $\mathsf {D}^* \Phi = (\nabla \Phi _{ij})_{ij}$
. More examples with discussion can be found in Section
7
.
$\mathsf {D}^* \Phi = (\nabla \Phi _{ij})_{ij}$
. More examples with discussion can be found in Section
7
.
Definition 3.4.
A measure
![]() $\mathsf{G} \in \mathcal {M}(Q_a^b, \mathbb {S}^n)$
connects
$\mathsf{G} \in \mathcal {M}(Q_a^b, \mathbb {S}^n)$
connects
![]() $\mathsf {G}_a, \mathsf {G}_b \in \mathcal {M}(\Omega, \mathbb {S}^n_+)$
over the time interval
$\mathsf {G}_a, \mathsf {G}_b \in \mathcal {M}(\Omega, \mathbb {S}^n_+)$
over the time interval
![]() $[a,b]$
, if there exists
$[a,b]$
, if there exists
![]() $\mathsf {(q, R)} \in \mathcal {M}(Q_a^b, \mathbb {R}^{n \times k} \times \mathbb {M}^n)$
satisfying the following general matrix-valued continuity equation:
$\mathsf {(q, R)} \in \mathcal {M}(Q_a^b, \mathbb {R}^{n \times k} \times \mathbb {M}^n)$
satisfying the following general matrix-valued continuity equation:
The measures
![]() $\mathsf {G}_a$
and
$\mathsf {G}_a$
and
![]() $\mathsf{G}_b$
are referred to as the initial and final distributions of
$\mathsf{G}_b$
are referred to as the initial and final distributions of
![]() $\mathsf {G}$
, respectively. Moreover, we denote by
$\mathsf {G}$
, respectively. Moreover, we denote by
![]() $\mathcal {CE}([a,b];\,\mathsf {G}_a, \mathsf {G}_b)$
the set of the measures
$\mathcal {CE}([a,b];\,\mathsf {G}_a, \mathsf {G}_b)$
the set of the measures
![]() $\mathsf {(G,q, R)} \in \mathcal {M}(Q_a^b,\mathbb {X})$
satisfying (3.13).
$\mathsf {(G,q, R)} \in \mathcal {M}(Q_a^b,\mathbb {X})$
satisfying (3.13).
Remark 3.5. It is easy to derive the distributional equation of (3.13):
with the measure
![]() $\mathsf {q}$
satisfying a homogeneous boundary condition on
$\mathsf {q}$
satisfying a homogeneous boundary condition on
![]() $\partial \Omega$
. Indeed, assume that
$\partial \Omega$
. Indeed, assume that
![]() $\mathsf {q}$
admits a smooth density
$\mathsf {q}$
admits a smooth density
![]() $q$
with respect to the Lebesgue measure. Note that for
$q$
with respect to the Lebesgue measure. Note that for
![]() $\mathsf {D}^* = a + \partial _{x_i}$
with
$\mathsf {D}^* = a + \partial _{x_i}$
with
![]() $\mathsf {D} = - a + \partial _{x_i}$
(
$\mathsf {D} = - a + \partial _{x_i}$
(
![]() $a \in \mathbb {R}$
), a direct integration by parts gives, for smooth real functions
$a \in \mathbb {R}$
), a direct integration by parts gives, for smooth real functions
![]() $f,g$
on
$f,g$
on
![]() $\Omega$
,
$\Omega$
,
We then have, by linearity and noting
![]() $\widehat {\partial _{x_k}} = \mathrm {i} \xi _k$
, for a general
$\widehat {\partial _{x_k}} = \mathrm {i} \xi _k$
, for a general
![]() $\mathsf {D}^*$
,
$\mathsf {D}^*$
,
It follows that the boundary condition
![]() $\widehat {\mathsf {D}_1}({-}\mathrm {i} \nu )(q) = 0$
holds for
$\widehat {\mathsf {D}_1}({-}\mathrm {i} \nu )(q) = 0$
holds for
![]() $\mathsf {q}$
satisfying (3.13). In the case of
$\mathsf {q}$
satisfying (3.13). In the case of
![]() $\mathsf {D} = \mathrm {div}$
for
$\mathsf {D} = \mathrm {div}$
for
![]() $\mathsf {q} \in \mathcal {M}(Q, \mathbb {R}^{d})$
, we see that
$\mathsf {q} \in \mathcal {M}(Q, \mathbb {R}^{d})$
, we see that
![]() $\widehat {\mathsf {D}_1}({-}\mathrm {i} \nu )(q) = 0$
is the familiar no-flux boundary condition
$\widehat {\mathsf {D}_1}({-}\mathrm {i} \nu )(q) = 0$
is the familiar no-flux boundary condition
![]() $\nu \cdot q = 0$
.
$\nu \cdot q = 0$
.
Remark 3.6. We give an intuitive interpretation of (3.14) as a continuity equation. Recall the homogeneous parts
![]() $\mathsf {D}_0$
and
$\mathsf {D}_0$
and
![]() $\mathsf {D}_1$
of
$\mathsf {D}_1$
of
![]() $\mathsf {D}$
with
$\mathsf {D}$
with
![]() $\mathsf{D}_0 \in \mathcal {L}(\mathbb{R}^{n \times k},\mathbb{S}^n)$
and
$\mathsf{D}_0 \in \mathcal {L}(\mathbb{R}^{n \times k},\mathbb{S}^n)$
and
![]() $\mathsf {D}_1$
vanishing when acting on constant functions. It allows us to split
$\mathsf {D}_1$
vanishing when acting on constant functions. It allows us to split
![]() $\mathsf {D}\mathsf {q}$
into two parts:
$\mathsf {D}\mathsf {q}$
into two parts:
![]() $\mathsf {D}_0\mathsf {q}$
and
$\mathsf {D}_0\mathsf {q}$
and
![]() $\mathsf {D}_1\mathsf {q}$
, where
$\mathsf {D}_1\mathsf {q}$
, where
![]() $\mathsf {D}_0\mathsf {q}$
and
$\mathsf {D}_0\mathsf {q}$
and
![]() $\mathsf {D}_1\mathsf {q}$
describe the mass transportation between components of
$\mathsf {D}_1\mathsf {q}$
describe the mass transportation between components of
![]() $\mathsf {G}$
and the transportation in space, respectively. Moreover, the condition
$\mathsf {G}$
and the transportation in space, respectively. Moreover, the condition
![]() $\mathsf {D}^*(I) = 0$
can be regarded as a conservativity condition in the sense that if
$\mathsf {D}^*(I) = 0$
can be regarded as a conservativity condition in the sense that if
![]() $\mathsf {R} = 0$
, then
$\mathsf {R} = 0$
, then
![]() $Tr\mathsf {G}_t(\Omega ) = Tr \mathsf {G}_0(\Omega )$
for any
$Tr\mathsf {G}_t(\Omega ) = Tr \mathsf {G}_0(\Omega )$
for any
![]() $t$
; see Proposition 3.13.
$t$
; see Proposition 3.13.
The following elementary lemma gives the absolute continuity of the time marginal of
![]() $\mathsf {G}$
.
$\mathsf {G}$
.
Lemma 3.7.
Let
![]() $\mathsf {(G,q,R)} \in \mathcal {CE}([a,b];\,\mathsf {G}_a,\mathsf {G}_b)$
with
$\mathsf {(G,q,R)} \in \mathcal {CE}([a,b];\,\mathsf {G}_a,\mathsf {G}_b)$
with
![]() $\mathsf {G}_a, \mathsf {G}_b \in \mathcal {M}(\Omega, \mathbb {S}^n_+)$
. It holds that
$\mathsf {G}_a, \mathsf {G}_b \in \mathcal {M}(\Omega, \mathbb {S}^n_+)$
. It holds that
![]() $\pi ^t_\# \mathsf {G} \in \mathcal {M}([a,b],\mathbb {S}^n)$
has the distributional derivative
$\pi ^t_\# \mathsf {G} \in \mathcal {M}([a,b],\mathbb {S}^n)$
has the distributional derivative
![]() $(\pi _\#^t \mathsf {R})^{\mathrm {sym}} \in \mathcal {M}([a,b],\mathbb {S}^n)$
in
$(\pi _\#^t \mathsf {R})^{\mathrm {sym}} \in \mathcal {M}([a,b],\mathbb {S}^n)$
in
![]() $t$
. If, further,
$t$
. If, further,
![]() $\mathsf {G} \in \mathcal {M}(Q_a^b,\mathbb {S}_+^n)$
is a positive semi-definite matrix-valued measure over
$\mathsf {G} \in \mathcal {M}(Q_a^b,\mathbb {S}_+^n)$
is a positive semi-definite matrix-valued measure over
![]() $Q_a^b$
, then
$Q_a^b$
, then
![]() $\pi ^t_\# |\mathsf {G}| \ll \mathrm {d} t$
.
$\pi ^t_\# |\mathsf {G}| \ll \mathrm {d} t$
.
Proof. It suffices to consider
![]() $[a,b] = [0,1]$
. By (3.13) with test functions
$[a,b] = [0,1]$
. By (3.13) with test functions
![]() $\Phi (t,x) = \phi (t) \in C_c^1((0,1),\mathbb {S}^n)$
, we have
$\Phi (t,x) = \phi (t) \in C_c^1((0,1),\mathbb {S}^n)$
, we have
which implies that
![]() $(\pi _\#^t \mathsf {R})^{\mathrm {sym}}$
is the distributional derivative of
$(\pi _\#^t \mathsf {R})^{\mathrm {sym}}$
is the distributional derivative of
![]() $\pi _\#^t \mathsf {G}$
. Note that
$\pi _\#^t \mathsf {G}$
. Note that
![]() $\pi ^t_\# \mathsf {G}$
and
$\pi ^t_\# \mathsf {G}$
and
![]() $\pi ^t_\# \mathsf {R}$
are Radon measures (since every finite Borel measure on
$\pi ^t_\# \mathsf {R}$
are Radon measures (since every finite Borel measure on
![]() $[0,1]$
is regular). There exists a matrix-valued bounded variation function
$[0,1]$
is regular). There exists a matrix-valued bounded variation function
![]() $M(t)$
that generates the Radon measure
$M(t)$
that generates the Radon measure
![]() $\pi ^t_\# \mathsf {R}$
[Reference Gerald42, Theorem 3.29]. It follows from (3.15) that
$\pi ^t_\# \mathsf {R}$
[Reference Gerald42, Theorem 3.29]. It follows from (3.15) that
for some
![]() $C \in \mathbb {S}^n$
[Reference Gerald42, Theorem 3.36]. bIf
$C \in \mathbb {S}^n$
[Reference Gerald42, Theorem 3.36]. bIf
![]() $\mathsf {G} \in \mathcal {M}(Q_a^b,\mathbb {S}_+^n)$
, then (3.16) and (2.2) readily give
$\mathsf {G} \in \mathcal {M}(Q_a^b,\mathbb {S}_+^n)$
, then (3.16) and (2.2) readily give
![]() $Tr \pi ^t_\# \mathsf {G} \sim |\pi ^t_\# \mathsf {G}| \ll \mathrm {d} t$
, which further yields
$Tr \pi ^t_\# \mathsf {G} \sim |\pi ^t_\# \mathsf {G}| \ll \mathrm {d} t$
, which further yields
![]() $\pi ^t_\# |\mathsf {G}| \ll \mathrm {d} t$
by noting
$\pi ^t_\# |\mathsf {G}| \ll \mathrm {d} t$
by noting
![]() $Tr \pi ^t_\# \mathsf {G} = \pi ^t_\# Tr \mathsf {G} \sim \pi ^t_\# |\mathsf {G}|$
.
$Tr \pi ^t_\# \mathsf {G} = \pi ^t_\# Tr \mathsf {G} \sim \pi ^t_\# |\mathsf {G}|$
.
3.3. Weighted Wasserstein–Bures distance
We are now ready to define a class of distances on
![]() $\mathcal {M}(\Omega, \mathbb {S}^n_+)$
by minimising the action functional
$\mathcal {M}(\Omega, \mathbb {S}^n_+)$
by minimising the action functional
![]() $\mathcal {J}_{\Lambda, Q}(\mu )$
over the solutions to the continuity equation (3.13).
$\mathcal {J}_{\Lambda, Q}(\mu )$
over the solutions to the continuity equation (3.13).
Definition 3.8.
The weighted Wasserstein–Bures distance between
![]() $\mathsf {G}_0, \mathsf {G}_1 \in \mathcal {M}(\Omega, \mathbb {S}_+^n)$
is defined by
$\mathsf {G}_0, \mathsf {G}_1 \in \mathcal {M}(\Omega, \mathbb {S}_+^n)$
is defined by
We remark that the quantity
![]() $\mathcal {J}_{\Lambda, Q}(\mu )$
can be understood as the energy of the measure
$\mathcal {J}_{\Lambda, Q}(\mu )$
can be understood as the energy of the measure
![]() $\mu \in \mathcal {CE}([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
. The following a priori estimate shows that
$\mu \in \mathcal {CE}([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
. The following a priori estimate shows that
![]() $\mathcal {CE}([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
is nonempty and
$\mathcal {CE}([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
is nonempty and
![]() $\rm {WB}_{\Lambda }(\mathsf {G}_0,\mathsf {G}_1)$
is always finite, which means that the problem (
$\rm {WB}_{\Lambda }(\mathsf {G}_0,\mathsf {G}_1)$
is always finite, which means that the problem (
![]() $\mathcal {P}$
) is well defined.
$\mathcal {P}$
) is well defined.
Lemma 3.9.
Given
![]() $\mathsf {G}_0,\mathsf {G}_1 \in \mathcal {M}(\Omega, \mathbb {S}^n_+)$
, let
$\mathsf {G}_0,\mathsf {G}_1 \in \mathcal {M}(\Omega, \mathbb {S}^n_+)$
, let
![]() $\lambda \in \mathcal {M}(\Omega, \mathbb {R}_+)$
be a reference measure such that
$\lambda \in \mathcal {M}(\Omega, \mathbb {R}_+)$
be a reference measure such that
![]() $|\mathsf {G}_0|, |\mathsf {G}_1| \ll \lambda$
. Then there exists
$|\mathsf {G}_0|, |\mathsf {G}_1| \ll \lambda$
. Then there exists
![]() $\mu = \mathsf {(G,0,R)} \in \mathcal {CE}([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
with finite
$\mu = \mathsf {(G,0,R)} \in \mathcal {CE}([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
with finite
![]() $\mathcal {J}_{\Lambda, Q}(\mu )$
. Moreover, it holds that
$\mathcal {J}_{\Lambda, Q}(\mu )$
. Moreover, it holds that
where
![]() $G_{0,\lambda }$
and
$G_{0,\lambda }$
and
![]() $G_{1,\lambda }$
are densities of
$G_{1,\lambda }$
are densities of
![]() $\mathsf {G}_0$
and
$\mathsf {G}_0$
and
![]() $\mathsf {G}_1$
with respect to
$\mathsf {G}_1$
with respect to
![]() $\lambda$
.
$\lambda$
.
Proof. We omit the subscript
![]() $\lambda$
of
$\lambda$
of
![]() $G_{0,\lambda }$
and
$G_{0,\lambda }$
and
![]() $G_{1,\lambda }$
for simplicity. We define measures
$G_{1,\lambda }$
for simplicity. We define measures
and
which satisfies
![]() $\mu = \mathsf {(G,0,R)} \in \mathcal {CE}([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
and
$\mu = \mathsf {(G,0,R)} \in \mathcal {CE}([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
and
![]() $\mathrm {Ran} \big ( \frac {\mathrm {d} \mathsf {R}}{\mathrm {d} t \otimes \lambda } \big ) \subset \mathrm {Ran} \big ( \frac {\mathrm {d} \mathsf {G}}{\mathrm {d} t \otimes \lambda } \big )$
for
$\mathrm {Ran} \big ( \frac {\mathrm {d} \mathsf {R}}{\mathrm {d} t \otimes \lambda } \big ) \subset \mathrm {Ran} \big ( \frac {\mathrm {d} \mathsf {G}}{\mathrm {d} t \otimes \lambda } \big )$
for
![]() $\mathrm {d} t \otimes \lambda$
-a.e. Moreover, we note
$\mathrm {d} t \otimes \lambda$
-a.e. Moreover, we note
from the relation:
![]() $ \mathrm {Ker}\big (\sqrt {G_0} + t (\sqrt {G_1} - \sqrt {G_0})\big ) = \mathrm {Ker} \big (\sqrt {G_0}\big ) \cap \mathrm {Ker} \big (\sqrt {G_1}\big )\subset \mathrm {Ker}\big (\sqrt {G_1} - \sqrt {G_0}\big )$
. Then, we compute
$ \mathrm {Ker}\big (\sqrt {G_0} + t (\sqrt {G_1} - \sqrt {G_0})\big ) = \mathrm {Ker} \big (\sqrt {G_0}\big ) \cap \mathrm {Ker} \big (\sqrt {G_1}\big )\subset \mathrm {Ker}\big (\sqrt {G_1} - \sqrt {G_0}\big )$
. Then, we compute
for
![]() $\mu$
defined above. The proof is completed by the submultiplicativity of the Frobenius norm.
$\mu$
defined above. The proof is completed by the submultiplicativity of the Frobenius norm.
Remark 3.10. The proof of Lemma 3.9 uses
![]() $\mathrm {Ran} (\Lambda _2) = \mathbb {R}^n$
from the assumption
$\mathrm {Ran} (\Lambda _2) = \mathbb {R}^n$
from the assumption
![]() $\Lambda _2 \in \mathbb {S}^n_{++}$
we made before (3.8). If we only assume
$\Lambda _2 \in \mathbb {S}^n_{++}$
we made before (3.8). If we only assume
![]() $\Lambda _2 \in \mathbb {S}^n_{+}$
, the distance
$\Lambda _2 \in \mathbb {S}^n_{+}$
, the distance
![]() $\mathrm {WB}_\Lambda$
may be only well-defined (i.e., finite) on a subset of
$\mathrm {WB}_\Lambda$
may be only well-defined (i.e., finite) on a subset of
![]() $\mathcal {M}(\Omega, \mathbb {S}^n_+)$
.
$\mathcal {M}(\Omega, \mathbb {S}^n_+)$
.
Remark 3.11.
![]() $\mathrm {WB}_{(0,\Lambda _2)}$
is the matricial Hellinger distance
$\mathrm {WB}_{(0,\Lambda _2)}$
is the matricial Hellinger distance
![]() $d_H$
in [Reference Monsaingeon and Vorotnikov73
, Definition 4.1], up to a transformation. Indeed, recalling Lemma
3.3
, we have that if
$d_H$
in [Reference Monsaingeon and Vorotnikov73
, Definition 4.1], up to a transformation. Indeed, recalling Lemma
3.3
, we have that if
![]() $\Lambda _1 = 0$
, then
$\Lambda _1 = 0$
, then
![]() $\mathsf {q}$
must be zero and (
$\mathsf {q}$
must be zero and (
![]() $\mathcal {P}$
) reduces to
$\mathcal {P}$
) reduces to
For a given
![]() $S \in \mathbb {S}^n_{++}$
, we introduce a linear map
$S \in \mathbb {S}^n_{++}$
, we introduce a linear map
![]() $g_{S}(A) \,:\!=\, S A S : \mathbb {S}^n_{+} \to \mathbb {S}^n_{+}$
with the inverse
$g_{S}(A) \,:\!=\, S A S : \mathbb {S}^n_{+} \to \mathbb {S}^n_{+}$
with the inverse
![]() $g_{S^{-1}}$
. It is easy to see that
$g_{S^{-1}}$
. It is easy to see that
![]() $\mathsf {(G,0,R)} \in \mathcal {CE}([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
if and only if
$\mathsf {(G,0,R)} \in \mathcal {CE}([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
if and only if
![]() $(g_{\Lambda _2^{-1}}(\mathsf {G}),0, g_{\Lambda _2^{-1}}(\mathsf {R})) \in \mathcal {CE}([0,1];\,g_{\Lambda _2^{-1}}(\mathsf {G}_0),g_{\Lambda _2^{-1}}(\mathsf {G}_1))$
, and there holds
$(g_{\Lambda _2^{-1}}(\mathsf {G}),0, g_{\Lambda _2^{-1}}(\mathsf {R})) \in \mathcal {CE}([0,1];\,g_{\Lambda _2^{-1}}(\mathsf {G}_0),g_{\Lambda _2^{-1}}(\mathsf {G}_1))$
, and there holds
![]() $\mathcal {J}_{(0,\Lambda _2),Q}(\mathsf {(G,0,R)}) = \mathcal {J}_{(0,I),Q}(g_{\Lambda _2^{-1}}(\mathsf {G}),0, g_{\Lambda _2^{-1}}(\mathsf {R}))$
. Therefore, we have
$\mathcal {J}_{(0,\Lambda _2),Q}(\mathsf {(G,0,R)}) = \mathcal {J}_{(0,I),Q}(g_{\Lambda _2^{-1}}(\mathsf {G}),0, g_{\Lambda _2^{-1}}(\mathsf {R}))$
. Therefore, we have
From [Reference Monsaingeon and Vorotnikov73
, Definition 4.1] and Theorem
4.5
below, one can see that
![]() $\mathrm {WB}_{(0,I)}$
is nothing else than the convex formulation of the Hellinger distance
$\mathrm {WB}_{(0,I)}$
is nothing else than the convex formulation of the Hellinger distance
![]() $d_H$
, up to a constant. We refer the readers to [Reference Monsaingeon and Vorotnikov73
, Lemma 4.3 and Theorem 2] for the properties of the Hellinger distance and its relation with the Bures-Wasserstein distance on
$d_H$
, up to a constant. We refer the readers to [Reference Monsaingeon and Vorotnikov73
, Lemma 4.3 and Theorem 2] for the properties of the Hellinger distance and its relation with the Bures-Wasserstein distance on
![]() $\mathbb {S}^n_+$
[10].
$\mathbb {S}^n_+$
[10].
3.4. A priori estimate
Thanks to Lemma3.9, the optimisation (𝒫) can be equivalently taken over the following set:
Before we proceed, we give some auxiliary results. First, we introduce
where
![]() $\lVert \cdot \rVert _{L^2_{\mathsf {G}}(\mathcal {X})}$
is defined by (2.3). By an argument similar to the one for Lemma4.1 below, we have that the conjugate function (2.6) of
$\lVert \cdot \rVert _{L^2_{\mathsf {G}}(\mathcal {X})}$
is defined by (2.3). By an argument similar to the one for Lemma4.1 below, we have that the conjugate function (2.6) of
![]() $\mathcal {J}^*_{\Lambda, \mathcal {X}}(\mathsf {G},u,W)$
with respect to
$\mathcal {J}^*_{\Lambda, \mathcal {X}}(\mathsf {G},u,W)$
with respect to
![]() $(u,W)$
is exactly
$(u,W)$
is exactly
![]() $\mathcal {J}_{\Lambda, \mathcal {X}}(\mathsf {G},\mathsf {q},\mathsf {R})$
. Moreover, there holds
$\mathcal {J}_{\Lambda, \mathcal {X}}(\mathsf {G},\mathsf {q},\mathsf {R})$
. Moreover, there holds
Since
![]() $\mathcal {J}_{\Lambda, \mathcal {X}}(\mathsf {G}, \mathsf {q},\mathsf {R})$
and
$\mathcal {J}_{\Lambda, \mathcal {X}}(\mathsf {G}, \mathsf {q},\mathsf {R})$
and
![]() $\mathcal {J}_{\Lambda, \mathcal {X}}^*(\mathsf {G}, u, W)$
are homogeneous of degree
$\mathcal {J}_{\Lambda, \mathcal {X}}^*(\mathsf {G}, u, W)$
are homogeneous of degree
![]() $2$
in
$2$
in
![]() $(\mathsf {q},\mathsf {R})$
and
$(\mathsf {q},\mathsf {R})$
and
![]() $(u,W)$
, respectively, by (3.21), it holds that for
$(u,W)$
, respectively, by (3.21), it holds that for
![]() $\mathsf {(G,q,R)} \in \mathcal {M}(\mathcal {X},\mathbb {X})$
and
$\mathsf {(G,q,R)} \in \mathcal {M}(\mathcal {X},\mathbb {X})$
and
![]() $(u,W) \in L^\infty _{|\mathsf {(G,q,R)}|}(\mathcal {X}, \mathbb {R}^{n \times k} \times \mathbb {M}^n)$
,
$(u,W) \in L^\infty _{|\mathsf {(G,q,R)}|}(\mathcal {X}, \mathbb {R}^{n \times k} \times \mathbb {M}^n)$
,
We minimise the right-hand side of (3.22) with respect to
![]() $\gamma$
and obtain
$\gamma$
and obtain
where we have used non-negativity of
![]() $\mathcal {J}_{\Lambda, \mathcal {X}}$
and
$\mathcal {J}_{\Lambda, \mathcal {X}}$
and
![]() $\mathcal {J}_{\Lambda, \mathcal {X}}^*$
.
$\mathcal {J}_{\Lambda, \mathcal {X}}^*$
.
Second, we observe from formulas (3.2) and (3.8) and Lemmas2.3 and 3.3 that for
![]() $\mu = (\mathsf {G},\mathsf {q},\mathsf {R}) \in \mathcal {M}(\mathcal {X},\mathbb {X})$
with
$\mu = (\mathsf {G},\mathsf {q},\mathsf {R}) \in \mathcal {M}(\mathcal {X},\mathbb {X})$
with
![]() $\mathcal {J}_{\Lambda, \mathcal {X}}(\mu ) \lt +\infty$
, the functions
$\mathcal {J}_{\Lambda, \mathcal {X}}(\mu ) \lt +\infty$
, the functions
![]() $G_\lambda ^\dagger q_\lambda \Lambda _1^\dagger$
and
$G_\lambda ^\dagger q_\lambda \Lambda _1^\dagger$
and
![]() $G_\lambda ^\dagger R_\lambda \Lambda _2^{-1}$
are well defined, Borel measurable and independent of the reference measure
$G_\lambda ^\dagger R_\lambda \Lambda _2^{-1}$
are well defined, Borel measurable and independent of the reference measure
![]() $\lambda$
(hence we omit the subscript
$\lambda$
(hence we omit the subscript
![]() $\lambda$
in the sequel for simplicity), and there holds
$\lambda$
in the sequel for simplicity), and there holds
We now give useful a priori bounds for measures
![]() $\mathsf {q}$
and
$\mathsf {q}$
and
![]() $\mathsf {R}$
.
$\mathsf {R}$
.
Lemma 3.12.
For
![]() $\mu = (\mathsf {G},\mathsf {q},\mathsf {R}) \in \mathcal {M}(\mathcal {X},\mathbb {X})$
with
$\mu = (\mathsf {G},\mathsf {q},\mathsf {R}) \in \mathcal {M}(\mathcal {X},\mathbb {X})$
with
![]() $\mathcal {J}_{\Lambda, \mathcal {X}}(\mu ) \lt +\infty$
, it holds that for
$\mathcal {J}_{\Lambda, \mathcal {X}}(\mu ) \lt +\infty$
, it holds that for
![]() $E \in \mathscr{B}(\mathcal {X})$
,
$E \in \mathscr{B}(\mathcal {X})$
,
Proof. Recall that there exist bounded measurable functions
![]() $\sigma _{q}$
and
$\sigma _{q}$
and
![]() $\sigma _{R}$
with
$\sigma _{R}$
with
![]() $ \lVert \sigma _{q} \rVert _{\mathrm {F}} = \lVert \sigma _{R} \rVert _{\mathrm {F}} = 1$
such that
$ \lVert \sigma _{q} \rVert _{\mathrm {F}} = \lVert \sigma _{R} \rVert _{\mathrm {F}} = 1$
such that
![]() $\mathrm {d} \mathsf {q} = \sigma _{q}\, \mathrm {d} |\mathsf {q}|$
and
$\mathrm {d} \mathsf {q} = \sigma _{q}\, \mathrm {d} |\mathsf {q}|$
and
![]() $\mathrm {d} \mathsf {R} = \sigma _{R} \,\mathrm {d} |\mathsf {R}|$
. Taking
$\mathrm {d} \mathsf {R} = \sigma _{R} \,\mathrm {d} |\mathsf {R}|$
. Taking
![]() $\mathsf {R} = 0$
and
$\mathsf {R} = 0$
and
![]() $(u,W) = (\chi _E \sigma _q, 0)$
in (3.23) for
$(u,W) = (\chi _E \sigma _q, 0)$
in (3.23) for
![]() $E \in \mathscr {B}(\mathcal {X})$
, we obtain
$E \in \mathscr {B}(\mathcal {X})$
, we obtain
by (3.24) and the following estimate derived from (3.20) and (2.4):
Similarly, by taking
![]() $\mathsf {q} = 0$
and
$\mathsf {q} = 0$
and
![]() $(u,W) = (0, \chi _E \sigma _R)$
in (3.23), we obtain the estimate for
$(u,W) = (0, \chi _E \sigma _R)$
in (3.23), we obtain the estimate for
![]() $\mathsf {R}$
in (3.25).
$\mathsf {R}$
in (3.25).
With the help of the above lemma, the following proposition holds.
Proposition 3.13.
Let
![]() $\mu = \mathsf {(G,q,R)}\in \mathcal {CE}_\infty ([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
with
$\mu = \mathsf {(G,q,R)}\in \mathcal {CE}_\infty ([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
with
![]() $\mathsf {G}_0,\mathsf {G}_1 \in \mathcal {M}(\Omega, \mathbb {S}^n_+)$
. Then,
$\mathsf {G}_0,\mathsf {G}_1 \in \mathcal {M}(\Omega, \mathbb {S}^n_+)$
. Then,
-
(i)
 $\mathsf {G} \in \mathcal {M}(Q,\mathbb {S}^n_+)$
and
$\mathsf {G} \in \mathcal {M}(Q,\mathbb {S}^n_+)$
and
 $\pi _\#^t |\mathsf {G}| \ll \mathrm {d} t$
. Moreover,
$\pi _\#^t |\mathsf {G}| \ll \mathrm {d} t$
. Moreover,
 $\mu$
can be disintegrated as
(3.26)where
$\mu$
can be disintegrated as
(3.26)where \begin{equation} \mu = \int _0^1 \delta _t \otimes (\mathsf {G}_t, \mathsf {q}_t, \mathsf {R}_t)\, \mathrm {d} t\,, \end{equation}
\begin{equation} \mu = \int _0^1 \delta _t \otimes (\mathsf {G}_t, \mathsf {q}_t, \mathsf {R}_t)\, \mathrm {d} t\,, \end{equation}
 $(\mathsf {G}_t, \mathsf {q}_t, \mathsf {R}_t) \in \mathcal {M}(\Omega, \mathbb {X})$
for
$(\mathsf {G}_t, \mathsf {q}_t, \mathsf {R}_t) \in \mathcal {M}(\Omega, \mathbb {X})$
for
 $\mathrm {d} t$
-a.e.
$\mathrm {d} t$
-a.e.
 $t \in [0,1]$
.
$t \in [0,1]$
.
-
(ii) There exists a weak* continuous curve
 $\big \{\widetilde {\mathsf {G}}\big \}_{t \in [0,1]}$
in
$\big \{\widetilde {\mathsf {G}}\big \}_{t \in [0,1]}$
in
 $\mathcal {M}(\Omega, \mathbb {S}^n_+)$
such that
$\mathcal {M}(\Omega, \mathbb {S}^n_+)$
such that
 $\mathsf {G}_t = \widetilde {\mathsf {G}}_t$
for a.e.
$\mathsf {G}_t = \widetilde {\mathsf {G}}_t$
for a.e.
 $t \in [0,1]$
and, for any interval
$t \in [0,1]$
and, for any interval
 $[t_0,t_1] \subset [0,1]$
, it holds that
(3.27)Moreover, there holds, for some
$[t_0,t_1] \subset [0,1]$
, it holds that
(3.27)Moreover, there holds, for some \begin{equation} \int _{Q_{t_0}^{t_1}} \partial _t\Phi \cdot \mathrm {d} \mathsf {G} + \mathsf {D}^* \Phi \cdot \mathrm {d} \mathsf {q} + \Phi \cdot \mathrm {d} \mathsf {R} = \int _{\Omega } \Phi _{t_1} \cdot \mathrm {d} \widetilde {\mathsf {G}}_{t_1} - \int _{\Omega } \Phi _{t_0} \cdot \mathrm {d} \widetilde {\mathsf {G}}_{t_0}\,, \quad \forall \Phi \in C^1(Q_{t_0}^{t_1},\mathbb {S}^n)\,. \end{equation}
\begin{equation} \int _{Q_{t_0}^{t_1}} \partial _t\Phi \cdot \mathrm {d} \mathsf {G} + \mathsf {D}^* \Phi \cdot \mathrm {d} \mathsf {q} + \Phi \cdot \mathrm {d} \mathsf {R} = \int _{\Omega } \Phi _{t_1} \cdot \mathrm {d} \widetilde {\mathsf {G}}_{t_1} - \int _{\Omega } \Phi _{t_0} \cdot \mathrm {d} \widetilde {\mathsf {G}}_{t_0}\,, \quad \forall \Phi \in C^1(Q_{t_0}^{t_1},\mathbb {S}^n)\,. \end{equation}
 $C \gt 0$
,(3.28)
$C \gt 0$
,(3.28) \begin{align} Tr \widetilde {\mathsf {G}}_t(\Omega ) \le C \left (Tr \mathsf {G}_0 (\Omega ) + \lVert G^\dagger R \Lambda _2^{-1} \rVert ^2_{L_{\mathsf {G}}^2(Q)}\lVert \Lambda _2 \rVert _{\mathrm {F}}^2\right ),\quad \forall t \in [0,1]\,. \end{align}
\begin{align} Tr \widetilde {\mathsf {G}}_t(\Omega ) \le C \left (Tr \mathsf {G}_0 (\Omega ) + \lVert G^\dagger R \Lambda _2^{-1} \rVert ^2_{L_{\mathsf {G}}^2(Q)}\lVert \Lambda _2 \rVert _{\mathrm {F}}^2\right ),\quad \forall t \in [0,1]\,. \end{align}
Remark 3.14. By Proposition 3.13, we can identify a measure
![]() $\mu = (\mathsf {G}, \mathsf {q},\mathsf {R})\in \mathcal {CE}_\infty ([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
with a family of measures
$\mu = (\mathsf {G}, \mathsf {q},\mathsf {R})\in \mathcal {CE}_\infty ([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
with a family of measures
![]() $\{\mu _t = (\mathsf {G}_t, \mathsf {q}_t,\mathsf {R}_t)\}_{t \in [0,1]}$
in
$\{\mu _t = (\mathsf {G}_t, \mathsf {q}_t,\mathsf {R}_t)\}_{t \in [0,1]}$
in
![]() $\mathcal {M}(\Omega, \mathbb {X})$
via the disintegration (3.26), where
$\mathcal {M}(\Omega, \mathbb {X})$
via the disintegration (3.26), where
![]() $\mathsf {G}_t$
is weak* continuous. We also remark that one can alternatively define the matrix-valued continuity equation (3.13) by testing against functions
$\mathsf {G}_t$
is weak* continuous. We also remark that one can alternatively define the matrix-valued continuity equation (3.13) by testing against functions
![]() $\Phi \in C^1(Q,\mathbb {S}^n)$
compactly supported in
$\Phi \in C^1(Q,\mathbb {S}^n)$
compactly supported in
![]() $(0,1)\times \Omega$
as in [1, Chapter 8] (in this case the right-hand side of (3.13) vanishes), and consider its solution
$(0,1)\times \Omega$
as in [1, Chapter 8] (in this case the right-hand side of (3.13) vanishes), and consider its solution
![]() $\mu = (\mathsf {G}, \mathsf {q},\mathsf {R}) \in \mathcal {M}(Q,\mathbb {X})$
with finite energy
$\mu = (\mathsf {G}, \mathsf {q},\mathsf {R}) \in \mathcal {M}(Q,\mathbb {X})$
with finite energy
![]() $\mathcal {J}_{\Lambda, Q}(\mu ) \lt +\infty$
. In this setting, a similar analysis by disintegration shows that
$\mathcal {J}_{\Lambda, Q}(\mu ) \lt +\infty$
. In this setting, a similar analysis by disintegration shows that
![]() $\mathsf {G}$
still has the weak* continuous representation
$\mathsf {G}$
still has the weak* continuous representation
![]() $\{\mathsf {G}_t\}_{t \in [0,1]}$
, and then the initial and final distributions
$\{\mathsf {G}_t\}_{t \in [0,1]}$
, and then the initial and final distributions
![]() $\mathsf {G}_0$
and
$\mathsf {G}_0$
and
![]() $\mathsf {G}_1$
can be obtained from the limits as
$\mathsf {G}_1$
can be obtained from the limits as
![]() $t \to 0$
and
$t \to 0$
and
![]() $t \to 1$
of
$t \to 1$
of
![]() $\mathsf {G}_t$
, respectively. In this work, we always stick to Definition 3.4 with temporal boundary conditions
$\mathsf {G}_t$
, respectively. In this work, we always stick to Definition 3.4 with temporal boundary conditions
![]() $\mathsf {G}_0$
and
$\mathsf {G}_0$
and
![]() $\mathsf {G}_1$
to avoid any confusion.
$\mathsf {G}_1$
to avoid any confusion.
Proof. (i) First, note from [Reference Ambrosio, Gigli and Savaré1, Theorem 5.3.1] that
![]() $\mu$
can be disintegrated with respect to
$\mu$
can be disintegrated with respect to
![]() $\nu = \pi ^t_\# |\mu |$
as
$\nu = \pi ^t_\# |\mu |$
as
![]() $\mu = \int _0^1 \delta _t \otimes \mu _t\, \mathrm {d} \nu$
, where
$\mu = \int _0^1 \delta _t \otimes \mu _t\, \mathrm {d} \nu$
, where
![]() $\mu _t \in \mathcal {M}(\Omega, \mathbb {X})$
for
$\mu _t \in \mathcal {M}(\Omega, \mathbb {X})$
for
![]() $\nu$
-a.e.
$\nu$
-a.e.
![]() $t \in [0,1]$
. Then, by Lemmas3.3 and 3.7, we have
$t \in [0,1]$
. Then, by Lemmas3.3 and 3.7, we have
![]() $\mathsf {G} \in \mathcal {M}(Q,\mathbb {S}^n_+)$
and
$\mathsf {G} \in \mathcal {M}(Q,\mathbb {S}^n_+)$
and
![]() $\nu \ll \pi ^t_\# | \mathsf {G}| \ll \mathrm {d} t$
on
$\nu \ll \pi ^t_\# | \mathsf {G}| \ll \mathrm {d} t$
on
![]() $[0,1]$
, which allows us to define
$[0,1]$
, which allows us to define
![]() $\widetilde {\mu }_t \,:\!=\, \mu _t \frac {\mathrm {d} \nu }{\mathrm {d} t}$
and disintegrate
$\widetilde {\mu }_t \,:\!=\, \mu _t \frac {\mathrm {d} \nu }{\mathrm {d} t}$
and disintegrate
![]() $\mu$
as
$\mu$
as
![]() $\mu = \int _0^1 \delta _t \otimes \widetilde {\mu }_t\, \mathrm {d} t$
.
$\mu = \int _0^1 \delta _t \otimes \widetilde {\mu }_t\, \mathrm {d} t$
.
(ii) Consider test functions
![]() $\Phi = a(t)\Psi (x)$
in (3.13) with
$\Phi = a(t)\Psi (x)$
in (3.13) with
![]() $a(t) \in C_c^1((0,1),\mathbb {R})$
and
$a(t) \in C_c^1((0,1),\mathbb {R})$
and
![]() $\Psi (x) \in C^1(\Omega, \mathbb {S}^n)$
. Then, by (3.26),
$\Psi (x) \in C^1(\Omega, \mathbb {S}^n)$
. Then, by (3.26),
![]() $\int _{\Omega } \Psi \cdot \mathrm {d} \mathsf {G}_t$
is absolutely continuous in
$\int _{\Omega } \Psi \cdot \mathrm {d} \mathsf {G}_t$
is absolutely continuous in
![]() $t$
with the weak derivative:
$t$
with the weak derivative:
Letting
![]() $\Psi = I$
in (3.29), we obtain
$\Psi = I$
in (3.29), we obtain
![]() $\partial _t Tr \mathsf {G}_t(\Omega ) = Tr \mathsf {R}^{\mathrm {sym}}_t(\Omega )$
a.e. by
$\partial _t Tr \mathsf {G}_t(\Omega ) = Tr \mathsf {R}^{\mathrm {sym}}_t(\Omega )$
a.e. by
![]() $\mathsf {D}^*(I) = 0$
, which implies that there exists a nonnegative function
$\mathsf {D}^*(I) = 0$
, which implies that there exists a nonnegative function
![]() $m(t) \in C([0,1],\mathbb {R})$
such that
$m(t) \in C([0,1],\mathbb {R})$
such that
![]() $Tr \mathsf {G}_t (\Omega ) = m(t)$
a.e. on
$Tr \mathsf {G}_t (\Omega ) = m(t)$
a.e. on
![]() $[0,1]$
and
$[0,1]$
and
By Lemma3.12, it follows from (3.30) that, from some
![]() $C \gt 0$
,
$C \gt 0$
,
We choose
![]() $t_0$
such that
$t_0$
such that
![]() $m(t_0) = \max _{t \in [0,1]} m(t)$
. Then (3.31) implies
$m(t_0) = \max _{t \in [0,1]} m(t)$
. Then (3.31) implies
which further gives, by an elementary calculation,
Then we have
With the above estimates, the existence of a weak* continuous representative of
![]() $\mathsf {G}_t$
and the formula (3.27) can be proved similarly to [Reference Ambrosio, Gigli and Savaré1, Lemma 8.1.2]. We sketch the argument for completeness. By (3.25) and (3.33), as well as (3.29), there exists a subset
$\mathsf {G}_t$
and the formula (3.27) can be proved similarly to [Reference Ambrosio, Gigli and Savaré1, Lemma 8.1.2]. We sketch the argument for completeness. By (3.25) and (3.33), as well as (3.29), there exists a subset
![]() $E \in [0,1]$
of Lebesgue measure zero such that
$E \in [0,1]$
of Lebesgue measure zero such that
![]() $Tr \mathsf {G}_t (\Omega ) = m(t)$
on
$Tr \mathsf {G}_t (\Omega ) = m(t)$
on
![]() $[0,1]\backslash E$
, and there holds, for any
$[0,1]\backslash E$
, and there holds, for any
![]() $t,s \in [0,1]\backslash E$
with
$t,s \in [0,1]\backslash E$
with
![]() $s \lt t$
and
$s \lt t$
and
![]() $\Psi \in C^1(\Omega, \mathbb {S}^n)$
,
$\Psi \in C^1(\Omega, \mathbb {S}^n)$
,
The estimate (3.34) allows us to uniquely extend
![]() $\{\mathsf {G}_t\}_{t \in [0,1]\backslash E}$
to a weak* continuous curve
$\{\mathsf {G}_t\}_{t \in [0,1]\backslash E}$
to a weak* continuous curve
![]() $\{\widetilde {\mathsf {G}}_t\}_{t \in [0,1]}$
in
$\{\widetilde {\mathsf {G}}_t\}_{t \in [0,1]}$
in
![]() $C^1(\Omega, \mathbb {S}^n)^*$
. Then, by the density of
$C^1(\Omega, \mathbb {S}^n)^*$
. Then, by the density of
![]() $C^1(\Omega, \mathbb {S}^n)$
in
$C^1(\Omega, \mathbb {S}^n)$
in
![]() $C(\Omega, \mathbb {S}^n)$
and the boundedness (3.33) of
$C(\Omega, \mathbb {S}^n)$
and the boundedness (3.33) of
![]() $\{Tr \widetilde {\mathsf {G}}_t (\Omega )\}_{t \in [0,1]}$
, the curve
$\{Tr \widetilde {\mathsf {G}}_t (\Omega )\}_{t \in [0,1]}$
, the curve
![]() $\{\widetilde {\mathsf {G}}_t\}_{t \in [0,1]}$
is also weak* continuous in
$\{\widetilde {\mathsf {G}}_t\}_{t \in [0,1]}$
is also weak* continuous in
![]() $\mathcal {M}(\Omega, \mathbb {S}^n)$
. The formula (3.27) follows from taking test functions
$\mathcal {M}(\Omega, \mathbb {S}^n)$
. The formula (3.27) follows from taking test functions
![]() $\Phi _\varepsilon (x,t) = \eta _\varepsilon (t)\Phi (t,x)$
in (3.13), where
$\Phi _\varepsilon (x,t) = \eta _\varepsilon (t)\Phi (t,x)$
in (3.13), where
![]() $\Phi \in C^1(Q,\mathbb {S}^n)$
and
$\Phi \in C^1(Q,\mathbb {S}^n)$
and
![]() $\eta _\varepsilon \in C_c^\infty ((t_0,t_1),\mathbb {R})$
with
$\eta _\varepsilon \in C_c^\infty ((t_0,t_1),\mathbb {R})$
with
![]() $0 \le \eta _\varepsilon \le 1$
,
$0 \le \eta _\varepsilon \le 1$
,
![]() $\lim _{\varepsilon \to 0}\eta _\varepsilon (t) = \chi _{(t_0,t_1)}(t)$
pointwisely and
$\lim _{\varepsilon \to 0}\eta _\varepsilon (t) = \chi _{(t_0,t_1)}(t)$
pointwisely and
![]() $\lim _{\varepsilon \to 0}\eta^{\prime}_\varepsilon = \delta _{t_0} - \delta _{t_1}$
in the distributional sense. Recalling
$\lim _{\varepsilon \to 0}\eta^{\prime}_\varepsilon = \delta _{t_0} - \delta _{t_1}$
in the distributional sense. Recalling
![]() $Tr \mathsf {G}_t (\Omega ) = m(t)$
a.e., by the weak* continuity of
$Tr \mathsf {G}_t (\Omega ) = m(t)$
a.e., by the weak* continuity of
![]() $\widetilde {\mathsf {G}}_t$
, we have
$\widetilde {\mathsf {G}}_t$
, we have
![]() $Tr \widetilde {\mathsf {G}}_t = m(t)$
. Then, the estimate (3.28) follows from (3.33).
$Tr \widetilde {\mathsf {G}}_t = m(t)$
. Then, the estimate (3.28) follows from (3.33).
3.5. Time and space scaling
By writing
![]() $\mathcal {J}_{\Lambda, Q}(\mu ) = \int _0^1\mathcal {J}_{\Lambda, \Omega }(\mu _t)\, \mathrm {d} t$
for
$\mathcal {J}_{\Lambda, Q}(\mu ) = \int _0^1\mathcal {J}_{\Lambda, \Omega }(\mu _t)\, \mathrm {d} t$
for
![]() $\mu \in \mathcal {CE}_\infty ([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
, the following Lemma is a simple consequence of the change of variable.
$\mu \in \mathcal {CE}_\infty ([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
, the following Lemma is a simple consequence of the change of variable.
Lemma 3.15.
Let
![]() $\mu \in \mathcal {CE}_\infty ([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
. It holds that
$\mu \in \mathcal {CE}_\infty ([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
. It holds that
-
1. Let
 $\mathsf {s}(t)\,:\,[0,1] \to [a,b]$
be a strictly increasing absolutely continuous map with an absolutely continuous inverse:
$\mathsf {s}(t)\,:\,[0,1] \to [a,b]$
be a strictly increasing absolutely continuous map with an absolutely continuous inverse:
 $\mathsf {t} = \mathsf {s}^{-1}$
. Then
$\mathsf {t} = \mathsf {s}^{-1}$
. Then
 $\widetilde {\mu } \,:\!=\, \int _a^b \delta _s \otimes (\mathsf {G}_{\mathsf {t}(s)}, \mathsf {t}^{\prime}(s) \mathsf {q}_{\mathsf {t}(s)}, \mathsf {t}^{\prime}(s) \mathsf {R}_{\mathsf {t}(s)})\, \mathrm {d} s \in \mathcal {CE}([a,b];\, \mathsf {G}_0,\mathsf {G}_1)$
. Moreover, we have
(3.35)
$\widetilde {\mu } \,:\!=\, \int _a^b \delta _s \otimes (\mathsf {G}_{\mathsf {t}(s)}, \mathsf {t}^{\prime}(s) \mathsf {q}_{\mathsf {t}(s)}, \mathsf {t}^{\prime}(s) \mathsf {R}_{\mathsf {t}(s)})\, \mathrm {d} s \in \mathcal {CE}([a,b];\, \mathsf {G}_0,\mathsf {G}_1)$
. Moreover, we have
(3.35) \begin{align} \int _0^1 \mathsf {t}^{\prime}(\mathsf {s}(t)) \mathcal {J}_{\Lambda, \Omega }(\mu _t)\, \mathrm {d} t = \int _a^b \mathcal {J}_{\Lambda, \Omega }(\widetilde {\mu }_s) \,\mathrm {d} s\,. \end{align}
\begin{align} \int _0^1 \mathsf {t}^{\prime}(\mathsf {s}(t)) \mathcal {J}_{\Lambda, \Omega }(\mu _t)\, \mathrm {d} t = \int _a^b \mathcal {J}_{\Lambda, \Omega }(\widetilde {\mu }_s) \,\mathrm {d} s\,. \end{align}
-
2. Let
 $T$
be a diffeomorphism on
$T$
be a diffeomorphism on
 $\mathbb {R}^d$
mapping from
$\mathbb {R}^d$
mapping from
 $\Omega$
to
$\Omega$
to
 $T(\Omega )$
and suppose that there exists
$T(\Omega )$
and suppose that there exists
 $\mathcal {T}_{\mathsf{D}^{*}}(x)\,:\, \Omega \to \mathcal {L}(\mathbb {R}^{n \times k})$
such that for
$\mathcal {T}_{\mathsf{D}^{*}}(x)\,:\, \Omega \to \mathcal {L}(\mathbb {R}^{n \times k})$
such that for
 $\Phi \in C_c^\infty (\mathbb {R}^d, \mathbb {S}^n)$
,(3.36)Then
$\Phi \in C_c^\infty (\mathbb {R}^d, \mathbb {S}^n)$
,(3.36)Then \begin{align} \mathcal {T}_{\mathsf{D}^{*}}[(\mathsf{D}^{*} \Phi )\circ T] \,:\!=\, \mathsf{D}^{*} (\Phi \circ T)\,. \end{align}
\begin{align} \mathcal {T}_{\mathsf{D}^{*}}[(\mathsf{D}^{*} \Phi )\circ T] \,:\!=\, \mathsf{D}^{*} (\Phi \circ T)\,. \end{align}
 $\widetilde {\mu } \,:\!=\, \int _0^1 \delta _t \otimes T_{\#} (\mathsf {G}_{t}, \mathcal {T}_{\mathsf {D}} \mathsf {q}_{t}, \mathsf {R}_{t})\, \mathrm {d} t \in \mathcal {CE}([0,1];\, T_{\#}\mathsf {G}_0, T_{\#}\mathsf {G}_1)$
on
$\widetilde {\mu } \,:\!=\, \int _0^1 \delta _t \otimes T_{\#} (\mathsf {G}_{t}, \mathcal {T}_{\mathsf {D}} \mathsf {q}_{t}, \mathsf {R}_{t})\, \mathrm {d} t \in \mathcal {CE}([0,1];\, T_{\#}\mathsf {G}_0, T_{\#}\mathsf {G}_1)$
on
 $T(\Omega )$
, where
$T(\Omega )$
, where
 $T_{\#}(\cdot )$
denotes the pushforward measure by
$T_{\#}(\cdot )$
denotes the pushforward measure by
 $T$
, and
$T$
, and
 $\mathcal {T}_{\mathsf {D}}$
is the transpose of
$\mathcal {T}_{\mathsf {D}}$
is the transpose of
 $\mathcal {T}_{\mathsf {D}^*}$
defined via
$\mathcal {T}_{\mathsf {D}^*}$
defined via
 $ (\mathcal {T}_{\mathsf {D}} q) \cdot p = q \cdot (\mathcal {T}_{\mathsf {D}^*} p)\,, \ \forall p,q \in \mathbb {R}^{n \times k}$
.
$ (\mathcal {T}_{\mathsf {D}} q) \cdot p = q \cdot (\mathcal {T}_{\mathsf {D}^*} p)\,, \ \forall p,q \in \mathbb {R}^{n \times k}$
.
Remark 3.16. The condition (3.36) is nontrivial and necessary for the second statement. Indeed, there holds
by Fourier transform, where
![]() $(\xi \cdot \nabla T(x))_j = \xi \cdot \partial _j T(x)$
. It follows that (3.36) is equivalent to a separation of variables:
$(\xi \cdot \nabla T(x))_j = \xi \cdot \partial _j T(x)$
. It follows that (3.36) is equivalent to a separation of variables:
![]() $\widehat {\mathsf {D}^*}(\xi \cdot \nabla T(x)) = \mathcal {T}_{\mathsf{D}^{*}}(x) \circ \widehat {\mathsf {D}^*}(\xi )$
. A sufficient condition for (3.36) is that
$\widehat {\mathsf {D}^*}(\xi \cdot \nabla T(x)) = \mathcal {T}_{\mathsf{D}^{*}}(x) \circ \widehat {\mathsf {D}^*}(\xi )$
. A sufficient condition for (3.36) is that
![]() $\widehat {\mathsf {D}^*}$
is homogeneous of degree
$\widehat {\mathsf {D}^*}$
is homogeneous of degree
![]() $0$
, or homogeneous of degree
$0$
, or homogeneous of degree
![]() $1$
with
$1$
with
![]() $T(x) = a x + b$
for
$T(x) = a x + b$
for
![]() $a \neq 0 \in \mathbb {R}$
and
$a \neq 0 \in \mathbb {R}$
and
![]() $b \in \mathbb {R}^d$
, which is enough for our purposes.
$b \in \mathbb {R}^d$
, which is enough for our purposes.
Remark 3.17. We connect the weight matrix
![]() $\Lambda _1$
and the space scaling. Let us consider
$\Lambda _1$
and the space scaling. Let us consider
![]() $\mu \in \mathcal {CE}_\infty ([0,1]; \mathsf {G}_0, \mathsf {G}_1)$
and
$\mu \in \mathcal {CE}_\infty ([0,1]; \mathsf {G}_0, \mathsf {G}_1)$
and
![]() $\mathsf {D}^*$
be homogeneous of degree one for simplicity. Define
$\mathsf {D}^*$
be homogeneous of degree one for simplicity. Define
![]() $T(x) = a x\,:\, \Omega \to a \Omega$
and
$T(x) = a x\,:\, \Omega \to a \Omega$
and
![]() $\mathcal {T}_{\mathsf {D}} = a I$
. By Lemma 3.15, we have
$\mathcal {T}_{\mathsf {D}} = a I$
. By Lemma 3.15, we have
![]() $\widetilde {\mu } \,:\!=\, \int _0^1 \delta _t \otimes T_{\#} (\mathsf {G}_{t}, a \mathsf {q}_{t}, \mathsf {R}_{t}) \, \mathrm {d} t \in \mathcal {CE}_\infty ([0,1];\, T_{\#}\mathsf {G}_0, T_{\#}\mathsf {G}_1)$
. Then, a direct computation gives
$\widetilde {\mu } \,:\!=\, \int _0^1 \delta _t \otimes T_{\#} (\mathsf {G}_{t}, a \mathsf {q}_{t}, \mathsf {R}_{t}) \, \mathrm {d} t \in \mathcal {CE}_\infty ([0,1];\, T_{\#}\mathsf {G}_0, T_{\#}\mathsf {G}_1)$
. Then, a direct computation gives
Using Lemma3.15 with
![]() $\mathsf {s}(t) = (b - a) t + a \,:\, [0,1] \to [a,b]$
,
$\mathsf {s}(t) = (b - a) t + a \,:\, [0,1] \to [a,b]$
,
![]() $b \gt a \gt 0$
, we see that for
$b \gt a \gt 0$
, we see that for
![]() $\mu \in \mathcal {CE}_\infty ([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
, there exists
$\mu \in \mathcal {CE}_\infty ([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
, there exists
![]() $\widetilde {\mu } \in \mathcal {CE}_\infty ([a,b];\mathsf {G}_0,\mathsf {G}_1)$
such that
$\widetilde {\mu } \in \mathcal {CE}_\infty ([a,b];\mathsf {G}_0,\mathsf {G}_1)$
such that
and vice versa, which gives the equivalent characterisation of
![]() $\mathrm {WB}_{\Lambda }$
:
$\mathrm {WB}_{\Lambda }$
:
3.6. Compactness
We end the discussion of basic properties of
![]() $\mathcal {CE}_\infty ([0,1];\, \mathsf {G}_0, \mathsf {G}_1)$
with a compactness result.
$\mathcal {CE}_\infty ([0,1];\, \mathsf {G}_0, \mathsf {G}_1)$
with a compactness result.
Proposition 3.18.
Let
![]() $\mu ^n = (\mathsf {G}^n,\mathsf {q}^n,\mathsf {R}^n) \in \mathcal {CE}_\infty ([0,1];\, \mathsf {G}^n_0, \mathsf {G}^n_1)$
,
$\mu ^n = (\mathsf {G}^n,\mathsf {q}^n,\mathsf {R}^n) \in \mathcal {CE}_\infty ([0,1];\, \mathsf {G}^n_0, \mathsf {G}^n_1)$
,
![]() $n \ge 1$
, be a sequence of measures satisfying
$n \ge 1$
, be a sequence of measures satisfying
Then there exists a subsequence, still denoted by
![]() $\mu ^n$
, and a measure
$\mu ^n$
, and a measure
![]() $\mu = (\mathsf {G},\mathsf {q},\mathsf {R}) \in \mathcal {CE}_\infty ([0,1]; \mathsf {G}_0, \mathsf {G}_1)$
such that for every
$\mu = (\mathsf {G},\mathsf {q},\mathsf {R}) \in \mathcal {CE}_\infty ([0,1]; \mathsf {G}_0, \mathsf {G}_1)$
such that for every
![]() $t\in [0,1]$
,
$t\in [0,1]$
,
![]() $\mathsf {G}^n_t$
weak* converges to
$\mathsf {G}^n_t$
weak* converges to
![]() $\mathsf {G}_t$
in
$\mathsf {G}_t$
in
![]() $\mathcal {M}(\Omega, \mathbb {S}^{n})$
, and
$\mathcal {M}(\Omega, \mathbb {S}^{n})$
, and
![]() $ (\mathsf{q}^{\mathsf{n}}, \mathsf{R}^{\mathsf{n}})$
weak* converges to
$ (\mathsf{q}^{\mathsf{n}}, \mathsf{R}^{\mathsf{n}})$
weak* converges to
![]() $\mathsf {(q,R)}$
in
$\mathsf {(q,R)}$
in
![]() $\mathcal {M}(Q,\mathbb {R}^{n \times k} \times \mathbb {M}^n)$
. Moreover, it holds that, for
$\mathcal {M}(Q,\mathbb {R}^{n \times k} \times \mathbb {M}^n)$
. Moreover, it holds that, for
![]() $0\le a \lt b \le 1$
,
$0\le a \lt b \le 1$
,
Proof. By (3.37), up to a subsequence, we can let
![]() $\mathsf {G}^n_0$
weak* converge to some
$\mathsf {G}^n_0$
weak* converge to some
![]() $\mathsf {G}_0 \in \mathcal {M}(\Omega, \mathbb {S}^n_+)$
. It is also clear from a priori estimates (3.25) and (3.28), as well as the assumption (3.37), that
$\mathsf {G}_0 \in \mathcal {M}(\Omega, \mathbb {S}^n_+)$
. It is also clear from a priori estimates (3.25) and (3.28), as well as the assumption (3.37), that
![]() $\{\mu ^n\}_{n \in \mathbb {N}}$
is bounded in
$\{\mu ^n\}_{n \in \mathbb {N}}$
is bounded in
![]() $\mathcal {M}(Q,\mathbb {X})$
. Hence, there exists a subsequence of
$\mathcal {M}(Q,\mathbb {X})$
. Hence, there exists a subsequence of
![]() $\{\mu ^n\}_{n \in \mathbb {N}}$
, still indexed by
$\{\mu ^n\}_{n \in \mathbb {N}}$
, still indexed by
![]() $n$
, weak* converging to some
$n$
, weak* converging to some
![]() $\mu \in \mathcal {M}(Q,\mathbb {X})$
. We next prove that the restriction of
$\mu \in \mathcal {M}(Q,\mathbb {X})$
. We next prove that the restriction of
![]() $\mu ^n$
on
$\mu ^n$
on
![]() $Q_a^b$
, i.e.,
$Q_a^b$
, i.e.,
![]() $\mu ^n|_{Q_a^b}$
, weak* converges to
$\mu ^n|_{Q_a^b}$
, weak* converges to
![]() $\mu |_{Q_a^b}$
in
$\mu |_{Q_a^b}$
in
![]() $\mathcal {M}(Q_a^b,\mathbb {X})$
for any
$\mathcal {M}(Q_a^b,\mathbb {X})$
for any
![]() $ 0 \le a \le b \le 1$
. For this, again by (3.25) and (3.28), we have, for some
$ 0 \le a \le b \le 1$
. For this, again by (3.25) and (3.28), we have, for some
![]() $C \gt 0$
,
$C \gt 0$
,
which also holds for
![]() $\mu$
. Let
$\mu$
. Let
![]() $\eta (t)$
be a smooth function, compactly supported in
$\eta (t)$
be a smooth function, compactly supported in
![]() $[a,b]$
, with
$[a,b]$
, with
![]() $|\eta (t)| \le 1$
and
$|\eta (t)| \le 1$
and
![]() $\eta = 1$
on
$\eta = 1$
on
![]() $[a+\varepsilon, b - \varepsilon ]$
for some small
$[a+\varepsilon, b - \varepsilon ]$
for some small
![]() $\varepsilon$
. Then, for any
$\varepsilon$
. Then, for any
![]() $\Xi \in C(Q_a^b,\mathbb {X})$
, we define
$\Xi \in C(Q_a^b,\mathbb {X})$
, we define
![]() $\widetilde {\Xi }(t,x) = \eta (t) \Xi (t,x) \in C(Q,\mathbb {X})$
. The following estimate readily follows from the properties of
$\widetilde {\Xi }(t,x) = \eta (t) \Xi (t,x) \in C(Q,\mathbb {X})$
. The following estimate readily follows from the properties of
![]() $\eta$
and the estimate (3.39):
$\eta$
and the estimate (3.39):
Since
![]() $\mu ^n$
weak* converges to
$\mu ^n$
weak* converges to
![]() $\mu$
in
$\mu$
in
![]() $\mathcal {M}(Q,\mathbb {X})$
and
$\mathcal {M}(Q,\mathbb {X})$
and
![]() $\varepsilon$
is arbitrary, we have
$\varepsilon$
is arbitrary, we have
![]() $\big |\langle \mu ^n, \Xi \rangle _{Q_a^b} - \langle \mu, \Xi \rangle _{Q_a^b}\big | \to 0$
as
$\big |\langle \mu ^n, \Xi \rangle _{Q_a^b} - \langle \mu, \Xi \rangle _{Q_a^b}\big | \to 0$
as
![]() $n \to \infty$
for
$n \to \infty$
for
![]() $\Xi \in C(Q_a^b,\mathbb {X})$
. Then, (3.38) follows from the lower semicontinuity of
$\Xi \in C(Q_a^b,\mathbb {X})$
. Then, (3.38) follows from the lower semicontinuity of
![]() $\mathcal {J}_{\Lambda, Q_a^b}(\mu )$
. We now show the weak* convergence of
$\mathcal {J}_{\Lambda, Q_a^b}(\mu )$
. We now show the weak* convergence of
![]() $\mathsf {G}^n_t$
for every
$\mathsf {G}^n_t$
for every
![]() $t\in [0,1]$
. We note, by taking
$t\in [0,1]$
. We note, by taking
![]() $\Phi (s,x) = \chi _{[0,t]}(s) \Psi (x)$
in (3.27) with
$\Phi (s,x) = \chi _{[0,t]}(s) \Psi (x)$
in (3.27) with
![]() $\Psi (x)\in C^1(\Omega, \mathbb {S}^n)$
,
$\Psi (x)\in C^1(\Omega, \mathbb {S}^n)$
,
Then, using the weak* convergences of
![]() $\mathsf {G}^n_0$
in
$\mathsf {G}^n_0$
in
![]() $\mathcal {M}(\Omega, \mathbb {S}^n)$
and
$\mathcal {M}(\Omega, \mathbb {S}^n)$
and
![]() $(\mathsf {q}^n,\mathsf {R}^n)|_{Q_0^t}$
in
$(\mathsf {q}^n,\mathsf {R}^n)|_{Q_0^t}$
in
![]() $\mathcal {M}(Q_0^t,\mathbb {R}^{n \times k}\times \mathbb {M}^n)$
, we get the convergence of
$\mathcal {M}(Q_0^t,\mathbb {R}^{n \times k}\times \mathbb {M}^n)$
, we get the convergence of
![]() $ \langle \mathsf {G}^n_{t}, \Psi \rangle _{\Omega }$
as
$ \langle \mathsf {G}^n_{t}, \Psi \rangle _{\Omega }$
as
![]() $n \to \infty$
. The proof is completed by the density of
$n \to \infty$
. The proof is completed by the density of
![]() $C^1(\Omega, \mathbb {S}^n)$
in
$C^1(\Omega, \mathbb {S}^n)$
in
![]() $C(\Omega, \mathbb {S}^n)$
and the uniform boundedness of
$C(\Omega, \mathbb {S}^n)$
and the uniform boundedness of
![]() $Tr \mathsf {G}^n_t (\Omega )$
with respect to
$Tr \mathsf {G}^n_t (\Omega )$
with respect to
![]() $n$
from (3.28).
$n$
from (3.28).
4. Properties of weighted Wasserstein–Bures metrics
This section is devoted to the investigation of the convex optimisation problem (𝒫). We shall first show the existence of the minimiser and derive the corresponding optimality condition. We then explore its primal-dual formulations in more detail, which will lead to a Riemannian interpretation of
![]() $\mathrm {WB}_{\Lambda }$
in Section 5. Finally, we consider the dependence of
$\mathrm {WB}_{\Lambda }$
in Section 5. Finally, we consider the dependence of
![]() $\mathrm {WB}_{\Lambda }$
on the weight matrix
$\mathrm {WB}_{\Lambda }$
on the weight matrix
![]() $\Lambda$
.
$\Lambda$
.
4.1. Existence of minimiser and optimality condition
For our purpose, let us first define the Lagrangian of (𝒫) with the multiplier
![]() $\Phi \in C^1(Q, \mathbb {S}^n)$
:
$\Phi \in C^1(Q, \mathbb {S}^n)$
:
which allows us to write
By changing the order of
![]() $\sup$
and
$\sup$
and
![]() $\inf$
, a formal calculation via integration by parts gives the dual problem:
$\inf$
, a formal calculation via integration by parts gives the dual problem:
 \begin{align} \mathrm {WB}_{\Lambda }^2(\mathsf {G}_0,\mathsf {G}_1) & \ge \sup _\Phi \inf _\mu \mathcal {L}(\mu, \Phi ) \notag \\ & = \sup _{\Phi } \Big \{ \langle \mathsf {G}_1, \Phi _1 \rangle _\Omega - \langle \mathsf {G}_0, \Phi _0 \rangle _\Omega \,; \ \partial _t \Phi + \frac {1}{2} (\mathsf {D}^* \Phi ) \Lambda _1^2 (\mathsf {D}^* \Phi )^{\mathrm {T}} + \frac {1}{2} \Phi \Lambda _2^2 \Phi \preceq 0 \Big \}\,. \end{align}
\begin{align} \mathrm {WB}_{\Lambda }^2(\mathsf {G}_0,\mathsf {G}_1) & \ge \sup _\Phi \inf _\mu \mathcal {L}(\mu, \Phi ) \notag \\ & = \sup _{\Phi } \Big \{ \langle \mathsf {G}_1, \Phi _1 \rangle _\Omega - \langle \mathsf {G}_0, \Phi _0 \rangle _\Omega \,; \ \partial _t \Phi + \frac {1}{2} (\mathsf {D}^* \Phi ) \Lambda _1^2 (\mathsf {D}^* \Phi )^{\mathrm {T}} + \frac {1}{2} \Phi \Lambda _2^2 \Phi \preceq 0 \Big \}\,. \end{align}
We next use the Fenchel-Rockafellar theorem (Lemma2.5) to show that the duality gap is zero, which will also give the existence of the minimiser to (𝒫) and the optimality conditions. For this, we define
with
![]() $\mathcal {O}_\Lambda$
given in (3.1), which is a closed convex subset of
$\mathcal {O}_\Lambda$
given in (3.1), which is a closed convex subset of
![]() $C(Q,\mathbb {X})$
. We then define lower semicontinuous convex functions:
$C(Q,\mathbb {X})$
. We then define lower semicontinuous convex functions:
![]() $f(\Phi ) = \langle \mathsf {G}_1, \Phi _1 \rangle _\Omega - \langle \mathsf {G}_0, \Phi _0 \rangle _\Omega$
for
$f(\Phi ) = \langle \mathsf {G}_1, \Phi _1 \rangle _\Omega - \langle \mathsf {G}_0, \Phi _0 \rangle _\Omega$
for
![]() $\Phi \in C^1(Q,\mathbb {S}^n)$
and
$\Phi \in C^1(Q,\mathbb {S}^n)$
and
![]() $g(\Xi ) = \iota _{C(Q,\mathcal {O}_\Lambda )}(\Xi )$
for
$g(\Xi ) = \iota _{C(Q,\mathcal {O}_\Lambda )}(\Xi )$
for
![]() $\Xi \in C(Q,\mathbb {X})$
. We also introduce the bounded linear operator:
$\Xi \in C(Q,\mathbb {X})$
. We also introduce the bounded linear operator:
![]() $L\,:\, \Phi \in C^1(Q, \mathbb {S}^n) \to (\partial _t \Phi, \mathsf {D}^* \Phi, \Phi ) \in C(Q,\mathbb {X})$
with the dual operator
$L\,:\, \Phi \in C^1(Q, \mathbb {S}^n) \to (\partial _t \Phi, \mathsf {D}^* \Phi, \Phi ) \in C(Q,\mathbb {X})$
with the dual operator
![]() $L^*$
. These notions help us to write (4.1) as
$L^*$
. These notions help us to write (4.1) as
![]() $ \sup \{f(\Phi ) - g(L \Phi )\,;\ \Phi \in C^1(Q,\mathbb {S}^n)\}\,.$
$ \sup \{f(\Phi ) - g(L \Phi )\,;\ \Phi \in C^1(Q,\mathbb {S}^n)\}\,.$
We now verify the condition in Lemma2.5. We consider
![]() $\Phi = -\varepsilon t I + \frac {\varepsilon }{2} I \in C^1(Q,\mathbb {S}^n)$
. It is clear that
$\Phi = -\varepsilon t I + \frac {\varepsilon }{2} I \in C^1(Q,\mathbb {S}^n)$
. It is clear that
![]() $f(\Phi )$
is finite and
$f(\Phi )$
is finite and
![]() $L \Phi = ({-} \varepsilon I, 0, -\varepsilon t I + \frac {\varepsilon }{2} I)$
by
$L \Phi = ({-} \varepsilon I, 0, -\varepsilon t I + \frac {\varepsilon }{2} I)$
by
![]() $\mathsf {D}^*(I) = 0$
. By a simple calculation, we have
$\mathsf {D}^*(I) = 0$
. By a simple calculation, we have
which implies that for small enough
![]() $\varepsilon$
and any
$\varepsilon$
and any
![]() $(t,x)\in Q$
,
$(t,x)\in Q$
,
![]() $(L \Phi )(t,x)$
is in the interior of
$(L \Phi )(t,x)$
is in the interior of
![]() $\mathcal {O}_\Lambda$
and hence
$\mathcal {O}_\Lambda$
and hence
![]() $g$
is continuous at
$g$
is continuous at
![]() $L \Phi$
. Then Lemma2.5 readily gives
$L \Phi$
. Then Lemma2.5 readily gives
where
![]() $f^*(L^*\mu ) = \sup \{\langle \mu, L\Phi \rangle _Q - f(\Phi )\,;\ \Phi \in C^1(Q,\mathbb {S}^n)\}$
can be easily computed as
$f^*(L^*\mu ) = \sup \{\langle \mu, L\Phi \rangle _Q - f(\Phi )\,;\ \Phi \in C^1(Q,\mathbb {S}^n)\}$
can be easily computed as
![]() $\iota _{\mathcal {CE}([0,1];\,\mathsf {G}_0,\mathsf {G}_1)}$
by linearity of
$\iota _{\mathcal {CE}([0,1];\,\mathsf {G}_0,\mathsf {G}_1)}$
by linearity of
![]() $f$
, while
$f$
, while
![]() $g^*(\mu )$
is nothing else than
$g^*(\mu )$
is nothing else than
![]() $\mathcal {J}_{\Lambda, Q}(\mu )$
by the following lemma, which is a direct application of general results [Reference Bouchitté and Valadier13, Reference Rockafellar83]. We sketch the proof in Appendix A for completeness.
$\mathcal {J}_{\Lambda, Q}(\mu )$
by the following lemma, which is a direct application of general results [Reference Bouchitté and Valadier13, Reference Rockafellar83]. We sketch the proof in Appendix A for completeness.
Lemma 4.1.
Let
![]() $\mathcal {X}$
be a compact separable metric space and
$\mathcal {X}$
be a compact separable metric space and
![]() $C(\mathcal {X},\mathcal {O}_\Lambda )$
be defined in (4.2). Then, we have
$C(\mathcal {X},\mathcal {O}_\Lambda )$
be defined in (4.2). Then, we have
which is proper convex and lower semicontinuous with respect to the weak* topology of
![]() $\mathcal {M}(\mathcal {X},\mathbb {X})$
. Moreover, the subgradient
$\mathcal {M}(\mathcal {X},\mathbb {X})$
. Moreover, the subgradient
![]() $\partial \mathcal {J}_{\Lambda, \mathcal {X}}(\mu )$
in
$\partial \mathcal {J}_{\Lambda, \mathcal {X}}(\mu )$
in
![]() $C(\mathcal {X},\mathbb {X})$
is given as follows:
$C(\mathcal {X},\mathbb {X})$
is given as follows:
which is independent of the choice of the reference measure
![]() $\lambda$
such that
$\lambda$
such that
![]() $|\mu | \ll \lambda$
.
$|\mu | \ll \lambda$
.
By the above arguments, we have shown the following result.
Theorem 4.2.
The optimisation problem (
𝒫
) always admits a minimiser
![]() $\mu \in \mathcal {CE}([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
and a dual formulation with zero duality gap:
$\mu \in \mathcal {CE}([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
and a dual formulation with zero duality gap:
where the
![]() $\sup$
is attained at
$\sup$
is attained at
![]() $\Phi \in C^1(Q,\mathbb {S}^n)$
if and only if there exists
$\Phi \in C^1(Q,\mathbb {S}^n)$
if and only if there exists
![]() $\mu = \mathsf {(G,q,R)} \in \mathcal {CE}([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
such that
$\mu = \mathsf {(G,q,R)} \in \mathcal {CE}([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
such that
and
for
![]() $\lambda$
-a.e.
$\lambda$
-a.e.
![]() $(t,x) \in Q$
. In this case,
$(t,x) \in Q$
. In this case,
![]() $\mu$
is also the minimiser to the problem (
$\mu$
is also the minimiser to the problem (
![]() $\mathcal {P}$
).
$\mathcal {P}$
).
As a consequence of Lemma4.1 and the dual formulation (4.6), we have the sublinearity and the weak* lower semicontinuity of
![]() $\mathrm {WB}^2_{\Lambda }(\cdot, \cdot )$
.
$\mathrm {WB}^2_{\Lambda }(\cdot, \cdot )$
.
Corollary 4.3.
![]() $\mathrm {WB}^2_{\Lambda }(\cdot, \cdot )$
is sublinear: for
$\mathrm {WB}^2_{\Lambda }(\cdot, \cdot )$
is sublinear: for
![]() $\alpha \gt 0$
,
$\alpha \gt 0$
,
![]() $\mathsf {G}_0,\mathsf {G}_1,\widetilde {\mathsf {G}}_0,\widetilde {\mathsf {G}}_1 \in \mathcal {M}(\Omega, \mathbb {S}^n_+)$
, there holds
$\mathsf {G}_0,\mathsf {G}_1,\widetilde {\mathsf {G}}_0,\widetilde {\mathsf {G}}_1 \in \mathcal {M}(\Omega, \mathbb {S}^n_+)$
, there holds
Moreover,
![]() $\mathrm {WB}_{\Lambda }$
is lower semicontinuous with respect to the weak* topology, that is, for any sequences
$\mathrm {WB}_{\Lambda }$
is lower semicontinuous with respect to the weak* topology, that is, for any sequences
![]() $\{\mathsf {G}^n_0\}_{n \in \mathbb {N}}$
and
$\{\mathsf {G}^n_0\}_{n \in \mathbb {N}}$
and
![]() $\{\mathsf {G}^n_1\}_{n \in \mathbb {N}}$
in
$\{\mathsf {G}^n_1\}_{n \in \mathbb {N}}$
in
![]() $\mathcal {M}(\Omega, \mathbb {S}_+^n)$
that weak* converge to measures
$\mathcal {M}(\Omega, \mathbb {S}_+^n)$
that weak* converge to measures
![]() $\mathsf {G}_0, \mathsf {G}_1 \in \mathcal {M}(\Omega, \mathbb {S}_+^n)$
, respectively, there holds
$\mathsf {G}_0, \mathsf {G}_1 \in \mathcal {M}(\Omega, \mathbb {S}_+^n)$
, respectively, there holds
Proof. Noting that
![]() $\mathcal {J}_{\Lambda, Q}(\mu )$
is positively homogeneous and convex, and hence sublinear, the sublinearity of
$\mathcal {J}_{\Lambda, Q}(\mu )$
is positively homogeneous and convex, and hence sublinear, the sublinearity of
![]() $\mathrm {WB}^2_{\Lambda }(\cdot, \cdot )$
follows from definition (
$\mathrm {WB}^2_{\Lambda }(\cdot, \cdot )$
follows from definition (
![]() $\mathcal {P}$
) and the linearity of the continuity equation. For the weak* lower semicontinuity, by (4.6), for any
$\mathcal {P}$
) and the linearity of the continuity equation. For the weak* lower semicontinuity, by (4.6), for any
![]() $\Phi \in C^1(Q,\mathbb {S}^n)$
with
$\Phi \in C^1(Q,\mathbb {S}^n)$
with
![]() $\iota _{C(Q,\mathcal {O}_\Lambda )}(\partial _t \Phi, \mathsf {D}^* \Phi, \Phi ) = 0$
, there holds
$\iota _{C(Q,\mathcal {O}_\Lambda )}(\partial _t \Phi, \mathsf {D}^* \Phi, \Phi ) = 0$
, there holds
by the weak* convergence of
![]() $\mathsf {G}_0^n$
and
$\mathsf {G}_0^n$
and
![]() $\mathsf {G}_1^n$
. Then (4.10) follows by taking the
$\mathsf {G}_1^n$
. Then (4.10) follows by taking the
![]() $\sup$
of (4.11) over admissible
$\sup$
of (4.11) over admissible
![]() $\Phi$
.
$\Phi$
.
In addition, we have the following explicit characterisation of the minimiser (i.e., geodesic; see Corollary5.7) to (
![]() $\mathcal {P}$
) for inflating measures from optimality conditions (4.7) and (4.8), which extends [Reference Brenier and Vorotnikov16, Theorem 5] with a much simpler argument. For
$\mathcal {P}$
) for inflating measures from optimality conditions (4.7) and (4.8), which extends [Reference Brenier and Vorotnikov16, Theorem 5] with a much simpler argument. For
![]() $\mathsf {G} \in \mathcal {M}(\Omega, \mathbb {S}^n_+)$
and
$\mathsf {G} \in \mathcal {M}(\Omega, \mathbb {S}^n_+)$
and
![]() $A \in \mathbb {S}_+^n$
, we denote by
$A \in \mathbb {S}_+^n$
, we denote by
![]() $\mathsf {G}^A$
the inflating measure
$\mathsf {G}^A$
the inflating measure
![]() $A \mathsf {G} A \in \mathcal {M}(\Omega, \mathbb {S}^n_+)$
.
$A \mathsf {G} A \in \mathcal {M}(\Omega, \mathbb {S}^n_+)$
.
Proposition 4.4.
For
![]() $\mathsf {G} \in \mathcal {M}(\Omega, \mathbb {S}^n_+)$
and matrices
$\mathsf {G} \in \mathcal {M}(\Omega, \mathbb {S}^n_+)$
and matrices
![]() $A_0, A_1 \in \mathbb {S}_+^n$
, we have
$A_0, A_1 \in \mathbb {S}_+^n$
, we have
with the minimiser
![]() $(\mathsf {G}_*,\mathsf {q}_*,\mathsf {R}_*) \,:\!=\, (\mathsf {G}^{A_t}, 0, 2 A_t \mathsf {G} (A_1 - A_0)) \in \mathcal {M}(Q, \mathbb {X})$
, where
$(\mathsf {G}_*,\mathsf {q}_*,\mathsf {R}_*) \,:\!=\, (\mathsf {G}^{A_t}, 0, 2 A_t \mathsf {G} (A_1 - A_0)) \in \mathcal {M}(Q, \mathbb {X})$
, where
![]() $A_t \,:\!=\, tA_1 + (1- t)A_0$
for
$A_t \,:\!=\, tA_1 + (1- t)A_0$
for
![]() $t \in [0,1]$
.
$t \in [0,1]$
.
Proof. Let us first assume that
![]() $A_0$
and
$A_0$
and
![]() $A_1$
are invertible. By a direct calculation, we have
$A_1$
are invertible. By a direct calculation, we have
We define
![]() $\Phi = 2 A_t^{-1} (A_1- A_0)\Lambda _2^{-2}$
and find
$\Phi = 2 A_t^{-1} (A_1- A_0)\Lambda _2^{-2}$
and find
![]() $\mathsf {R}_* = \mathsf {G}^{A_t} \Phi \Lambda _2^2$
. It is also easy to see that
$\mathsf {R}_* = \mathsf {G}^{A_t} \Phi \Lambda _2^2$
. It is also easy to see that
![]() $(\mathsf {G}_*,\mathsf {q}_*,\mathsf {R}_*)$
defined above is in the set
$(\mathsf {G}_*,\mathsf {q}_*,\mathsf {R}_*)$
defined above is in the set
![]() $\mathcal {CE}\big ([0,1]; \mathsf {G}^{A_0},\mathsf {G}^{A_1}\big )$
. Moreover, recalling
$\mathcal {CE}\big ([0,1]; \mathsf {G}^{A_0},\mathsf {G}^{A_1}\big )$
. Moreover, recalling
![]() $ ((A + \varepsilon H)^{-1} - A^{-1})/\varepsilon \to - A^{-1}H A^{-1}$
as
$ ((A + \varepsilon H)^{-1} - A^{-1})/\varepsilon \to - A^{-1}H A^{-1}$
as
![]() $\varepsilon \to 0$
for invertible
$\varepsilon \to 0$
for invertible
![]() $A$
and
$A$
and
![]() $H \in \mathbb {M}^n$
[Reference Bhatia9], we have
$H \in \mathbb {M}^n$
[Reference Bhatia9], we have
By the above computations, we have verified the optimality conditions (4.7) and (4.8), which means that the measure
![]() $(\mathsf {G}_*,\mathsf {q}_*,\mathsf {R}_*)$
is the desired minimiser. Then, we can further compute
$(\mathsf {G}_*,\mathsf {q}_*,\mathsf {R}_*)$
is the desired minimiser. Then, we can further compute
For general
![]() $A_0,A_1 \in \mathbb {S}_+^n$
, we first see that
$A_0,A_1 \in \mathbb {S}_+^n$
, we first see that
![]() $\mu _* \,:\!=\, (\mathsf {G}^{A_t}, 0, 2 A_t \mathsf {G} (A_1 - A_0))$
as above still satisfies the continuity equation and its associated action functional
$\mu _* \,:\!=\, (\mathsf {G}^{A_t}, 0, 2 A_t \mathsf {G} (A_1 - A_0))$
as above still satisfies the continuity equation and its associated action functional
![]() $\mathcal {J}_{\Lambda, Q}(\mu _*)$
gives the right-hand side of (4.12) by
$\mathcal {J}_{\Lambda, Q}(\mu _*)$
gives the right-hand side of (4.12) by
![]() $\mathrm {Ran}(A_1 - A_0) \subset \mathrm {Ran}(A_t)$
, which also means
$\mathrm {Ran}(A_1 - A_0) \subset \mathrm {Ran}(A_t)$
, which also means
![]() $ \mathrm {WB}_\Lambda ^2(\mathsf {G}^{A_0}, \mathsf {G}^{A_1}) \le \mathcal {J}_{\Lambda, Q}(\mu _*)$
. To finish the proof, it suffices to show that the equality holds. For this, we consider
$ \mathrm {WB}_\Lambda ^2(\mathsf {G}^{A_0}, \mathsf {G}^{A_1}) \le \mathcal {J}_{\Lambda, Q}(\mu _*)$
. To finish the proof, it suffices to show that the equality holds. For this, we consider
![]() $A_i^\varepsilon = A_i + \varepsilon I \in \mathbb {S}_{++}^n$
for
$A_i^\varepsilon = A_i + \varepsilon I \in \mathbb {S}_{++}^n$
for
![]() $i = 0,1$
. Then, by triangle inequality of
$i = 0,1$
. Then, by triangle inequality of
![]() $\mathrm {WB}_\Lambda$
(see Proposition5.2 below) and Lemma3.9, we have
$\mathrm {WB}_\Lambda$
(see Proposition5.2 below) and Lemma3.9, we have
![]() $\mathrm {WB}_\Lambda (\mathsf {G}^{A^\varepsilon _0}, \mathsf {G}^{A^\varepsilon _1}) \to \mathrm {WB}_\Lambda (\mathsf {G}^{A_0}, \mathsf {G}^{A_1})$
as
$\mathrm {WB}_\Lambda (\mathsf {G}^{A^\varepsilon _0}, \mathsf {G}^{A^\varepsilon _1}) \to \mathrm {WB}_\Lambda (\mathsf {G}^{A_0}, \mathsf {G}^{A_1})$
as
![]() $\varepsilon \to 0$
. The proof is completed by
$\varepsilon \to 0$
. The proof is completed by
4.2. Primal-dual formulations
We proceed to study in more depth the optimality conditions by viewing
![]() $\mathsf {G}$
as the main variable and
$\mathsf {G}$
as the main variable and
![]() $\mathsf {(q,R)}$
as the control variable, which will be useful in Section 5. We first observe
$\mathsf {(q,R)}$
as the control variable, which will be useful in Section 5. We first observe
by taking the inf in (
![]() $\mathcal {P}$
) over
$\mathcal {P}$
) over
![]() $\mathsf {G}$
and
$\mathsf {G}$
and
![]() $(\mathsf {q},\mathsf {R})$
separately. Recall the formulation (3.24) of
$(\mathsf {q},\mathsf {R})$
separately. Recall the formulation (3.24) of
![]() $\mathcal {J}_{\Lambda, Q}(\mu )$
, which motivates us to introduce a weighted semi-inner product:
$\mathcal {J}_{\Lambda, Q}(\mu )$
, which motivates us to introduce a weighted semi-inner product:
and the associated seminorm
![]() $\lVert \cdot \rVert _{L^2_{\mathsf {G},\Lambda }(Q)}$
on the space of measurable functions valued in
$\lVert \cdot \rVert _{L^2_{\mathsf {G},\Lambda }(Q)}$
on the space of measurable functions valued in
![]() $\mathbb {R}^{n \times k} \times \mathbb {M}^n$
. The corresponding Hilbert space, denoted by
$\mathbb {R}^{n \times k} \times \mathbb {M}^n$
. The corresponding Hilbert space, denoted by
![]() $L^2_{\mathsf {G},\Lambda }(Q,\mathbb {R}^{n \times k} \times \mathbb {M}^n)$
, is defined as the quotient space by the subspace
$L^2_{\mathsf {G},\Lambda }(Q,\mathbb {R}^{n \times k} \times \mathbb {M}^n)$
, is defined as the quotient space by the subspace
![]() $\mathrm {Ker}\big (\lVert \cdot \rVert _{L^2_{\mathsf {G},\Lambda }(Q)}\big )$
. Hence, we can rewrite (3.24) as
$\mathrm {Ker}\big (\lVert \cdot \rVert _{L^2_{\mathsf {G},\Lambda }(Q)}\big )$
. Hence, we can rewrite (3.24) as
![]() $\mathcal {J}_{\Lambda, Q}(\mu ) = \lVert (G^\dagger q,G^\dagger R) \rVert ^2_{L^2_{\mathsf {G},\Lambda }(Q)}/2$
. Moreover, we define the set
$\mathcal {J}_{\Lambda, Q}(\mu ) = \lVert (G^\dagger q,G^\dagger R) \rVert ^2_{L^2_{\mathsf {G},\Lambda }(Q)}/2$
. Moreover, we define the set
and the associated energy functional: for
![]() $\mathsf {G} \in \mathcal {AC}([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
,
$\mathsf {G} \in \mathcal {AC}([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
,
We will see in Remark5.6 that
![]() $\mathcal {AC}([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
is closely related to the set of absolutely continuous curves in the metric space
$\mathcal {AC}([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
is closely related to the set of absolutely continuous curves in the metric space
![]() $(\mathcal {M}(\Omega, \mathbb {S}^n_+), \mathrm {WB}_{\Lambda })$
. With the help of these notions, (4.13) can be reformulated in a compact form:
$(\mathcal {M}(\Omega, \mathbb {S}^n_+), \mathrm {WB}_{\Lambda })$
. With the help of these notions, (4.13) can be reformulated in a compact form:
Similarly to (3.24), by Lemma3.3, we also note that for
![]() $\mathsf {(G,q,R)} \in \mathcal {CE}_\infty ([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
, the weak formulation (3.13) can be written as
$\mathsf {(G,q,R)} \in \mathcal {CE}_\infty ([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
, the weak formulation (3.13) can be written as
where
![]() $l_{\mathsf {G}}(\cdot )$
for
$l_{\mathsf {G}}(\cdot )$
for
![]() $\mathsf {G} \in \mathcal {AC}([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
is a linear functional on
$\mathsf {G} \in \mathcal {AC}([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
is a linear functional on
![]() $C^1(Q,\mathbb {S}^n)$
defined by
$C^1(Q,\mathbb {S}^n)$
defined by
Define an injective map
![]() $\Pi \,:\, \Phi \to (\mathsf {D}^* \Phi \Lambda _1^2, \Phi \Lambda _2^2)$
for
$\Pi \,:\, \Phi \to (\mathsf {D}^* \Phi \Lambda _1^2, \Phi \Lambda _2^2)$
for
![]() $\Phi \in C^1(Q,\mathbb {S}^n)$
and denote
$\Phi \in C^1(Q,\mathbb {S}^n)$
and denote
![]() $\widetilde {l}_{\mathsf {G}}\,:\!=\, l_{\mathsf {G}} \circ \Pi ^{-1}$
on the image of
$\widetilde {l}_{\mathsf {G}}\,:\!=\, l_{\mathsf {G}} \circ \Pi ^{-1}$
on the image of
![]() $\Pi$
. In view of (4.18), the functional
$\Pi$
. In view of (4.18), the functional
![]() $\widetilde {l}_{\mathsf {G}}$
can be uniquely extended to the space
$\widetilde {l}_{\mathsf {G}}$
can be uniquely extended to the space
with the norm estimate
We emphasise that such an extension is independent of the choice of
![]() $\mathsf {(q,R)}$
that satisfies
$\mathsf {(q,R)}$
that satisfies
![]() $\mathsf {(G,q,R)} \in \mathcal {CE}_\infty ([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
.
$\mathsf {(G,q,R)} \in \mathcal {CE}_\infty ([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
.
Next, we show that (4.16) admits a unique minimiser
![]() $\mathsf {(q,R)}$
that satisfies the equality in (4.21). Note that
$\mathsf {(q,R)}$
that satisfies the equality in (4.21). Note that
![]() $(u,W)$
and
$(u,W)$
and
![]() $(u \mathbb {P}_{\Lambda _1}, W \mathbb {P}_{\Lambda _2})$
are equivalent in
$(u \mathbb {P}_{\Lambda _1}, W \mathbb {P}_{\Lambda _2})$
are equivalent in
![]() $L^2_{\mathsf {G},\Lambda }(Q,\mathbb {R}^{n \times k} \times \mathbb {M}^n)$
, where
$L^2_{\mathsf {G},\Lambda }(Q,\mathbb {R}^{n \times k} \times \mathbb {M}^n)$
, where
![]() $\mathbb {P}_{\Lambda _i}$
is the orthogonal projection to
$\mathbb {P}_{\Lambda _i}$
is the orthogonal projection to
![]() $\mathrm {Ran}(\Lambda _i)$
. Hence, for any
$\mathrm {Ran}(\Lambda _i)$
. Hence, for any
![]() $(u,W) \in L^2_{\mathsf {G},\Lambda }(Q,\mathbb {R}^{n \times k} \times \mathbb {M}^n)$
, we can assume
$(u,W) \in L^2_{\mathsf {G},\Lambda }(Q,\mathbb {R}^{n \times k} \times \mathbb {M}^n)$
, we can assume
![]() $\mathrm {Ran}(u^{\mathrm {T}}) \subset \mathrm {Ran} (\Lambda _1)$
and
$\mathrm {Ran}(u^{\mathrm {T}}) \subset \mathrm {Ran} (\Lambda _1)$
and
![]() $\mathrm {Ran}(W^{\mathrm {T}}) \subset \mathrm {Ran} (\Lambda _2)$
. Then, it holds that any
$\mathrm {Ran}(W^{\mathrm {T}}) \subset \mathrm {Ran} (\Lambda _2)$
. Then, it holds that any
![]() $L^2_{\mathsf {G},\Lambda }$
-field
$L^2_{\mathsf {G},\Lambda }$
-field
![]() $(u,W)$
satisfying
$(u,W)$
satisfying
![]() $ \langle (\mathsf {D}^* \Phi \Lambda _1^2, \Phi \Lambda _2^2), (u,W)\rangle _{L^2_{\mathsf {G},\Lambda }(Q)} = l_{\mathsf {G}}(\Phi )$
,
$ \langle (\mathsf {D}^* \Phi \Lambda _1^2, \Phi \Lambda _2^2), (u,W)\rangle _{L^2_{\mathsf {G},\Lambda }(Q)} = l_{\mathsf {G}}(\Phi )$
,
![]() $\forall \Phi \in C^1(Q,\mathbb {S}^n)$
, induces a measure
$\forall \Phi \in C^1(Q,\mathbb {S}^n)$
, induces a measure
![]() $\mathsf {(q,R)} \,:\!=\, (\mathsf {G} u,\mathsf {G}W)$
such that
$\mathsf {(q,R)} \,:\!=\, (\mathsf {G} u,\mathsf {G}W)$
such that
![]() $\mathsf {(G,q,R)} \in \mathcal {CE}_\infty ([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
. This observation implies that
$\mathsf {(G,q,R)} \in \mathcal {CE}_\infty ([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
. This observation implies that
![]() $\mathcal {J}^{\Lambda }_{\mathsf {G}_0,\mathsf {G}_1}(\mathsf {G})$
is actually a uniquely solvable minimum norm problem with an affine constraint:
$\mathcal {J}^{\Lambda }_{\mathsf {G}_0,\mathsf {G}_1}(\mathsf {G})$
is actually a uniquely solvable minimum norm problem with an affine constraint:
 \begin{align} \mathcal {J}^{\Lambda }_{\mathsf {G}_0,\mathsf {G}_1}(\mathsf {G}) &= \inf \Big \{\frac {1}{2} \lVert (u,W) \rVert ^2_{L^2_{\mathsf {G},\Lambda }(Q)}\,;\ (u,W) \in L^2_{\mathsf {G},\Lambda }(Q,\mathbb {R}^{n \times k} \times \mathbb {M}^n)\ \text {such that} \notag \\ \big \langle (\mathsf {D}^* \Phi \Lambda _1^2, \Phi \Lambda _2^2), (u,W) \big \rangle _{L^2_{\mathsf {G},\Lambda }(Q)} &= l_{\mathsf {G}}(\Phi )\,, \ \forall \Phi \in C^1(Q,\mathbb {S}^n) \Big \}\,. \end{align}
\begin{align} \mathcal {J}^{\Lambda }_{\mathsf {G}_0,\mathsf {G}_1}(\mathsf {G}) &= \inf \Big \{\frac {1}{2} \lVert (u,W) \rVert ^2_{L^2_{\mathsf {G},\Lambda }(Q)}\,;\ (u,W) \in L^2_{\mathsf {G},\Lambda }(Q,\mathbb {R}^{n \times k} \times \mathbb {M}^n)\ \text {such that} \notag \\ \big \langle (\mathsf {D}^* \Phi \Lambda _1^2, \Phi \Lambda _2^2), (u,W) \big \rangle _{L^2_{\mathsf {G},\Lambda }(Q)} &= l_{\mathsf {G}}(\Phi )\,, \ \forall \Phi \in C^1(Q,\mathbb {S}^n) \Big \}\,. \end{align}
The unique minimiser
![]() $(u_*,W_*)$
to (4.22) is given by the orthogonal projection of
$(u_*,W_*)$
to (4.22) is given by the orthogonal projection of
![]() $0$
on the constraint set, equivalently, the Riesz representation of the functional
$0$
on the constraint set, equivalently, the Riesz representation of the functional
![]() $\widetilde {l}_{\mathsf {G}}$
on the space
$\widetilde {l}_{\mathsf {G}}$
on the space
![]() $H_{\mathsf {G},\Lambda }(\mathsf {D}^*)$
. It then follows that
$H_{\mathsf {G},\Lambda }(\mathsf {D}^*)$
. It then follows that
![]() $(\mathsf {q}_*,\mathsf {R}_*) \,:\!=\, (\mathsf {G} u_*,\mathsf {G}W_*)$
is the desired minimiser to (4.16) and there holds
$(\mathsf {q}_*,\mathsf {R}_*) \,:\!=\, (\mathsf {G} u_*,\mathsf {G}W_*)$
is the desired minimiser to (4.16) and there holds
We summarise the above facts in the following useful result.
Theorem 4.5.
![]() $\mathrm {WB}^2_{\Lambda }(\mathsf {G}_0,\mathsf {G}_1)$
has the following representation:
$\mathrm {WB}^2_{\Lambda }(\mathsf {G}_0,\mathsf {G}_1)$
has the following representation:
where
![]() $(u_*, W_*)$
is the Riesz representation of
$(u_*, W_*)$
is the Riesz representation of
![]() $\widetilde {l}_{\mathsf {G}}$
in
$\widetilde {l}_{\mathsf {G}}$
in
![]() $H_{\mathsf {G},\Lambda }(\mathsf {D}^*)$
that uniquely solves the minimum norm problem (4.22).
$H_{\mathsf {G},\Lambda }(\mathsf {D}^*)$
that uniquely solves the minimum norm problem (4.22).
Moreover,
![]() $\mathcal {J}^{\Lambda }_{\mathsf {G}_0,\mathsf {G}_1}(\mathsf {G})$
admits the following dual formulation:
$\mathcal {J}^{\Lambda }_{\mathsf {G}_0,\mathsf {G}_1}(\mathsf {G})$
admits the following dual formulation:
Proof. It suffices to derive the dual formulation (4.24) of
![]() $\mathcal {J}^{\Lambda }_{\mathsf {G}_0,\mathsf {G}_1}$
. For this, we first note
$\mathcal {J}^{\Lambda }_{\mathsf {G}_0,\mathsf {G}_1}$
. For this, we first note
which further implies, by
![]() $(u_*, W_*) \in H_{\mathsf {G},\Lambda }(\mathsf {D}^*) \subset L^2_{\mathsf {G},\Lambda }(Q,\mathbb {R}^{n \times k} \times \mathbb {M}^n)$
, for any
$(u_*, W_*) \in H_{\mathsf {G},\Lambda }(\mathsf {D}^*) \subset L^2_{\mathsf {G},\Lambda }(Q,\mathbb {R}^{n \times k} \times \mathbb {M}^n)$
, for any
![]() $\Phi \in C^1(Q,\mathbb {S}^n)$
,
$\Phi \in C^1(Q,\mathbb {S}^n)$
,
 \begin{align} \mathcal {J}^{\Lambda }_{\mathsf {G}_0,\mathsf {G}_1}(\mathsf {G}) = \frac {1}{2}\lVert (u_*, W_*) \rVert _{L^2_{\mathsf {G},\Lambda }(Q)}^2 &\ge \langle (u_*, W_*), \big (\mathsf {D}^* \Phi \Lambda ^2_1, \Phi \Lambda _2^2 \big )\rangle _{L^2_{\mathsf {G},\Lambda }(Q)} - \frac {1}{2}\lVert ( \mathsf {D}^* \Phi \Lambda _1^2,\Phi \Lambda _2^2) \rVert ^2_{L^2_{\mathsf {G},\Lambda }(Q)}\notag \\ & = l_G(\Phi ) - \frac {1}{2}\lVert ( \mathsf {D}^* \Phi \Lambda _1^2,\Phi \Lambda _2^2) \rVert ^2_{L^2_{\mathsf {G},\Lambda }(Q)}\,. \end{align}
\begin{align} \mathcal {J}^{\Lambda }_{\mathsf {G}_0,\mathsf {G}_1}(\mathsf {G}) = \frac {1}{2}\lVert (u_*, W_*) \rVert _{L^2_{\mathsf {G},\Lambda }(Q)}^2 &\ge \langle (u_*, W_*), \big (\mathsf {D}^* \Phi \Lambda ^2_1, \Phi \Lambda _2^2 \big )\rangle _{L^2_{\mathsf {G},\Lambda }(Q)} - \frac {1}{2}\lVert ( \mathsf {D}^* \Phi \Lambda _1^2,\Phi \Lambda _2^2) \rVert ^2_{L^2_{\mathsf {G},\Lambda }(Q)}\notag \\ & = l_G(\Phi ) - \frac {1}{2}\lVert ( \mathsf {D}^* \Phi \Lambda _1^2,\Phi \Lambda _2^2) \rVert ^2_{L^2_{\mathsf {G},\Lambda }(Q)}\,. \end{align}
Then, recalling (4.20) and choosing a sequence
![]() $\{(\mathsf {D}^* \Phi _n \Lambda _1^2, \Phi _n \Lambda _2^2)\}$
with
$\{(\mathsf {D}^* \Phi _n \Lambda _1^2, \Phi _n \Lambda _2^2)\}$
with
![]() $\Phi _n \in C^1(Q,\mathbb {S}^n)$
in (4.25) that approximates
$\Phi _n \in C^1(Q,\mathbb {S}^n)$
in (4.25) that approximates
![]() $(u_*, W_*)$
gives the desired (4.24).
$(u_*, W_*)$
gives the desired (4.24).
4.3. Varying weight matrices
We regard
![]() $\mathrm {WB}_{\Lambda }$
as a family of distances indexed by
$\mathrm {WB}_{\Lambda }$
as a family of distances indexed by
![]() $\Lambda$
and investigate the behaviours of
$\Lambda$
and investigate the behaviours of
![]() $\mathrm {WB}_{\Lambda }$
and its minimiser when
$\mathrm {WB}_{\Lambda }$
and its minimiser when
![]() $\Lambda$
varies, in particular, when
$\Lambda$
varies, in particular, when
![]() $|\Lambda _1|$
or
$|\Lambda _1|$
or
![]() $|\Lambda _2|$
tends to zero or infinity. We give a partial answer to this question in the following proposition. For ease of exposition, we introduce
$|\Lambda _2|$
tends to zero or infinity. We give a partial answer to this question in the following proposition. For ease of exposition, we introduce
Proposition 4.6.
Let
![]() $\mathsf {G}_0,\mathsf {G}_1 \in \mathcal {M}(\Omega, \mathbb {S}^n_+)$
and
$\mathsf {G}_0,\mathsf {G}_1 \in \mathcal {M}(\Omega, \mathbb {S}^n_+)$
and
![]() $\mu _{*,\Lambda }$
denote the minimiser to
$\mu _{*,\Lambda }$
denote the minimiser to
![]() $\mathrm {WB}^2_\Lambda (\mathsf {G}_0,\mathsf {G}_1)$
(
$\mathrm {WB}^2_\Lambda (\mathsf {G}_0,\mathsf {G}_1)$
(
![]() $\mathcal {P}$
). It holds that
$\mathcal {P}$
). It holds that
![]() $\mathrm {WB}^2_{(\Lambda _1,\Lambda _2)}(\mathsf {G}_0,\mathsf {G}_1) \to \mathrm {WB}^2_{(0,\Lambda _2)}(\mathsf {G}_0,\mathsf {G}_1)$
as
$\mathrm {WB}^2_{(\Lambda _1,\Lambda _2)}(\mathsf {G}_0,\mathsf {G}_1) \to \mathrm {WB}^2_{(0,\Lambda _2)}(\mathsf {G}_0,\mathsf {G}_1)$
as
![]() $\lVert \Lambda _1 \rVert _{\mathrm {F}} \to 0$
, and for any sequence
$\lVert \Lambda _1 \rVert _{\mathrm {F}} \to 0$
, and for any sequence
![]() $\{ \Lambda _{1,j}\}_{j \in \mathbb {N}} \subset \mathbb {S}^k_+$
with
$\{ \Lambda _{1,j}\}_{j \in \mathbb {N}} \subset \mathbb {S}^k_+$
with
![]() $\lVert \Lambda _{1,j} \rVert _{\mathrm {F}} \to 0$
, the associated minimiser
$\lVert \Lambda _{1,j} \rVert _{\mathrm {F}} \to 0$
, the associated minimiser
![]() $\mu _{*,(\Lambda _{1,j},\Lambda _2)}$
, up to a subsequence, weak* converges to a minimiser
$\mu _{*,(\Lambda _{1,j},\Lambda _2)}$
, up to a subsequence, weak* converges to a minimiser
![]() $\mu _*$
to
$\mu _*$
to
![]() $\mathrm {WB}^2_{(0,\Lambda _2)}(\mathsf {G}_0,\mathsf {G}_1)$
.
$\mathrm {WB}^2_{(0,\Lambda _2)}(\mathsf {G}_0,\mathsf {G}_1)$
.
Proof. We first claim that
![]() $\lVert \Lambda _1 \rVert _{\mathrm {F}}^2\mathcal {J}^q_{\Lambda _1}(\mu _{*,\Lambda })$
and
$\lVert \Lambda _1 \rVert _{\mathrm {F}}^2\mathcal {J}^q_{\Lambda _1}(\mu _{*,\Lambda })$
and
![]() $\mathcal {J}^R_{\Lambda _2}(\mu _{*,\Lambda })$
are bounded when
$\mathcal {J}^R_{\Lambda _2}(\mu _{*,\Lambda })$
are bounded when
![]() $\lVert \Lambda _1 \rVert _{\mathrm {F}} \to 0$
, which, by estimates (3.25) and (3.28), implies that
$\lVert \Lambda _1 \rVert _{\mathrm {F}} \to 0$
, which, by estimates (3.25) and (3.28), implies that
![]() $\mu _{*,\Lambda }$
is bounded in
$\mu _{*,\Lambda }$
is bounded in
![]() $\mathcal {M}(Q,\mathbb {X})$
. For this, we consider the set
$\mathcal {M}(Q,\mathbb {X})$
. For this, we consider the set
Similarly to the proof of Lemma3.9, we have that
![]() $\mathcal {CE}_{\Lambda _1, q}$
is nonempty and contains at least one element with
$\mathcal {CE}_{\Lambda _1, q}$
is nonempty and contains at least one element with
![]() $\mathsf {q} = 0$
and
$\mathsf {q} = 0$
and
![]() $\min \{\mathcal {J}^q_{\Lambda _1}(\mu )\,; \ \mu \in \mathcal {CE}([0,1];\,\mathsf {G}_0,\mathsf {G}_1)\} = 0$
. Since
$\min \{\mathcal {J}^q_{\Lambda _1}(\mu )\,; \ \mu \in \mathcal {CE}([0,1];\,\mathsf {G}_0,\mathsf {G}_1)\} = 0$
. Since
![]() $\mu _{*,\Lambda }$
minimises
$\mu _{*,\Lambda }$
minimises
![]() $\mathcal {J}_{\Lambda, Q}(\cdot )$
, it follows that
$\mathcal {J}_{\Lambda, Q}(\cdot )$
, it follows that
Noting
![]() $\{\mathsf {(G,0,R)}\in \mathcal {CE}_{\Lambda _1, q}\} = \{\mathsf {(G,0,R)} \in \mathcal {CE}([0,1];\,\mathsf {G}_0,\mathsf {G}_1)\}$
, (4.28) yields that
$\{\mathsf {(G,0,R)}\in \mathcal {CE}_{\Lambda _1, q}\} = \{\mathsf {(G,0,R)} \in \mathcal {CE}([0,1];\,\mathsf {G}_0,\mathsf {G}_1)\}$
, (4.28) yields that
![]() $\mathcal {J}^R_{\Lambda _2}(\mu _{*,\Lambda })$
is bounded by a constant independent of
$\mathcal {J}^R_{\Lambda _2}(\mu _{*,\Lambda })$
is bounded by a constant independent of
![]() $\Lambda _1$
. Moreover, multiplying
$\Lambda _1$
. Moreover, multiplying
![]() $\lVert \Lambda _1 \rVert _{\mathrm {F}}^2$
on both sides of (4.28) and then letting
$\lVert \Lambda _1 \rVert _{\mathrm {F}}^2$
on both sides of (4.28) and then letting
![]() $\lVert \Lambda _1 \rVert _{\mathrm {F}} \to 0$
, we obtain
$\lVert \Lambda _1 \rVert _{\mathrm {F}} \to 0$
, we obtain
Then the boundedness of
![]() $\lVert \Lambda _1 \rVert _{\mathrm {F}}^2\mathcal {J}^q_{\Lambda _1}(\mu _{*,\Lambda })$
for small enough
$\lVert \Lambda _1 \rVert _{\mathrm {F}}^2\mathcal {J}^q_{\Lambda _1}(\mu _{*,\Lambda })$
for small enough
![]() $\lVert \Lambda _1 \rVert _{\mathrm {F}}$
follows. We complete the proof of the claim.
$\lVert \Lambda _1 \rVert _{\mathrm {F}}$
follows. We complete the proof of the claim.
By the boundedness of
![]() $\lVert \mu _{*,\Lambda } \rVert _{\mathrm {TV}}$
as
$\lVert \mu _{*,\Lambda } \rVert _{\mathrm {TV}}$
as
![]() $\lVert \Lambda _1 \rVert _{\mathrm {F}} \to 0$
, we are allowed to take a subsequence
$\lVert \Lambda _1 \rVert _{\mathrm {F}} \to 0$
, we are allowed to take a subsequence
![]() $\{\Lambda _{1,j}\}_{j \in \mathbb {N}}$
in
$\{\Lambda _{1,j}\}_{j \in \mathbb {N}}$
in
![]() $\mathbb {S}_+^n$
such that the minimiser
$\mathbb {S}_+^n$
such that the minimiser
![]() $\mu _{*,\widetilde {\Lambda }_j}$
with
$\mu _{*,\widetilde {\Lambda }_j}$
with
![]() $\widetilde {\Lambda }_j = (\Lambda _{1,j},\Lambda _2)$
weak* converges to a measure
$\widetilde {\Lambda }_j = (\Lambda _{1,j},\Lambda _2)$
weak* converges to a measure
![]() $\mu _* \in \mathcal {M}(Q,\mathbb {X})$
when
$\mu _* \in \mathcal {M}(Q,\mathbb {X})$
when
![]() $n \to \infty$
, which clearly satisfies
$n \to \infty$
, which clearly satisfies
![]() $\mu _* \in \mathcal {CE}([0,1];\, \mathsf {G}_0,\mathsf {G}_1)$
. Then, by the weak* lower semicontinuity of
$\mu _* \in \mathcal {CE}([0,1];\, \mathsf {G}_0,\mathsf {G}_1)$
. Then, by the weak* lower semicontinuity of
![]() $\mathcal {J}^R_{\Lambda _2}$
and (4.28), we have
$\mathcal {J}^R_{\Lambda _2}$
and (4.28), we have
The right-hand side of (4.30) is recognised as
![]() $\mathrm {WB}_{(0,\Lambda _2)}(\mathsf {G}_0,\mathsf {G}_1)$
and the inf is attained; see Remark3.11 and Theorem4.2. Also, by (3.25) and (4.29), it holds that the limit measure
$\mathrm {WB}_{(0,\Lambda _2)}(\mathsf {G}_0,\mathsf {G}_1)$
and the inf is attained; see Remark3.11 and Theorem4.2. Also, by (3.25) and (4.29), it holds that the limit measure
![]() $\mu _* \in \mathcal {CE}([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
is of the form
$\mu _* \in \mathcal {CE}([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
is of the form
![]() $\mu _* = (\mathsf{G}_{*}, \mathsf{0}, \mathsf{R}_{*})$
. The proof is completed by (4.30).
$\mu _* = (\mathsf{G}_{*}, \mathsf{0}, \mathsf{R}_{*})$
. The proof is completed by (4.30).
Proposition4.6 above tells us that the measure
![]() $\mathsf {q}$
is forced to be nearly zero, if the transportation part is given too much weight (i.e.,
$\mathsf {q}$
is forced to be nearly zero, if the transportation part is given too much weight (i.e.,
![]() $\lVert \Lambda _1 \rVert _{\mathrm {F}}$
is small, cf. (3.24)), equivalently, if the problem is on a large scale (cf. Remark3.17). It is also possible and interesting to consider other limiting regimes, e.g.,
$\lVert \Lambda _1 \rVert _{\mathrm {F}}$
is small, cf. (3.24)), equivalently, if the problem is on a large scale (cf. Remark3.17). It is also possible and interesting to consider other limiting regimes, e.g.,
![]() $\lVert \Lambda _1 \rVert _{\mathrm {F}} \to \infty$
,
$\lVert \Lambda _1 \rVert _{\mathrm {F}} \to \infty$
,
![]() $\lVert \Lambda _2 \rVert _{\mathrm {F}} \to 0$
, or only let part of eigenvalues of
$\lVert \Lambda _2 \rVert _{\mathrm {F}} \to 0$
, or only let part of eigenvalues of
![]() $\Lambda _i$
vanish, which, however, is beyond the scope of this work.
$\Lambda _i$
vanish, which, however, is beyond the scope of this work.
5. Geometric properties and Riemannian interpretation
In this section, we shall study the space
![]() $\mathcal {M}(\Omega, \mathbb {S}^n_+)$
equipped with the distance
$\mathcal {M}(\Omega, \mathbb {S}^n_+)$
equipped with the distance
![]() $\mathrm {WB}_{\Lambda }(\cdot, \cdot )$
from the metric point of view. In particular, we will prove that
$\mathrm {WB}_{\Lambda }(\cdot, \cdot )$
from the metric point of view. In particular, we will prove that
![]() $(\mathcal {M}(\Omega, \mathbb {S}^n_+),\mathrm {WB}_{\Lambda })$
is a complete geodesic space with a Riemannian interpretation. We first show that
$(\mathcal {M}(\Omega, \mathbb {S}^n_+),\mathrm {WB}_{\Lambda })$
is a complete geodesic space with a Riemannian interpretation. We first show that
![]() $\mathrm {WB}_{\Lambda }(\cdot, \cdot )$
is indeed a metric on
$\mathrm {WB}_{\Lambda }(\cdot, \cdot )$
is indeed a metric on
![]() $\mathcal {M}(\Omega, \mathbb {S}^n_+)$
, which is a simple corollary of the following characterisation of
$\mathcal {M}(\Omega, \mathbb {S}^n_+)$
, which is a simple corollary of the following characterisation of
![]() $\mathrm {WB}_{\Lambda }(\cdot, \cdot )$
by standard reparameterisation techniques (cf. [Reference Ambrosio, Gigli and Savaré1, Lemma 1.1.4] or [Reference Dolbeault, Nazaret and Savaré34, Theorem 5.4]). We denote by
$\mathrm {WB}_{\Lambda }(\cdot, \cdot )$
by standard reparameterisation techniques (cf. [Reference Ambrosio, Gigli and Savaré1, Lemma 1.1.4] or [Reference Dolbeault, Nazaret and Savaré34, Theorem 5.4]). We denote by
![]() $\widetilde {\mathcal {CE}}([a,b];\mathsf {G}_0,\mathsf {G}_1)$
the set of measures
$\widetilde {\mathcal {CE}}([a,b];\mathsf {G}_0,\mathsf {G}_1)$
the set of measures
![]() $\mu \in \mathcal {CE}([a,b];\mathsf {G}_0,\mathsf {G}_1)$
that can be disintegrated as
$\mu \in \mathcal {CE}([a,b];\mathsf {G}_0,\mathsf {G}_1)$
that can be disintegrated as
![]() $\mu = \int _a^b \delta _t \otimes \mu _t\, \mathrm {d} t$
. It is clear that
$\mu = \int _a^b \delta _t \otimes \mu _t\, \mathrm {d} t$
. It is clear that
![]() $\mathcal {CE}_\infty \subset \widetilde {\mathcal {CE}} \subset \mathcal {CE}$
.
$\mathcal {CE}_\infty \subset \widetilde {\mathcal {CE}} \subset \mathcal {CE}$
.
Lemma 5.1.
For
![]() $\mathsf {G}_0,\mathsf {G}_1 \in \mathcal {M}(\Omega, \mathbb {S}_+^n)$
and
$\mathsf {G}_0,\mathsf {G}_1 \in \mathcal {M}(\Omega, \mathbb {S}_+^n)$
and
![]() $b \gt a \gt 0$
, there holds
$b \gt a \gt 0$
, there holds
Moreover, the minimiser to the problem (
![]() $\mathcal {P}^{\prime}$
) gives a constant-speed minimiser
$\mathcal {P}^{\prime}$
) gives a constant-speed minimiser
![]() $\mu$
to (5.1), which satisfies
$\mu$
to (5.1), which satisfies
The proof is provided in Appendix A for completeness. The above lemma is an analogue of a well-known geometric fact that minimising the energy of a parametric curve is the same as minimising its length with constant-speed constraint [Reference Flaherty and do Carmo40]. The following result summarises some fundamental properties of
![]() $(\mathcal {M}(\Omega, \mathbb {S}^n_+), \mathrm {WB}_{\Lambda })$
.
$(\mathcal {M}(\Omega, \mathbb {S}^n_+), \mathrm {WB}_{\Lambda })$
.
Proposition 5.2.
![]() $(\mathcal {M}(\Omega, \mathbb {S}^n_+), \mathrm {WB}_{\Lambda })$
is a complete metric space. Moreover, the topology induced by the metric
$(\mathcal {M}(\Omega, \mathbb {S}^n_+), \mathrm {WB}_{\Lambda })$
is a complete metric space. Moreover, the topology induced by the metric
![]() $\mathrm {WB}_{\Lambda }$
is stronger than the weak* one, i.e.,
$\mathrm {WB}_{\Lambda }$
is stronger than the weak* one, i.e.,
![]() $\lim _{n \to \infty }\mathrm {WB}_{\Lambda }(\mathsf {G}^n,\mathsf {G}) = 0$
implies the weak* convergence of
$\lim _{n \to \infty }\mathrm {WB}_{\Lambda }(\mathsf {G}^n,\mathsf {G}) = 0$
implies the weak* convergence of
![]() $\mathsf {G}^n$
to
$\mathsf {G}^n$
to
![]() $\mathsf {G}$
.
$\mathsf {G}$
.
Remark 5.3. We should emphasise that stronger in Proposition 5.2 above means at least as strong as. In the special case of WFR distance (
![]() $\mathcal {P}_{\mathrm {WFR}}$
), one can show [Reference Liero, Mielke and Savaré65, Theorem 7.15] that
$\mathcal {P}_{\mathrm {WFR}}$
), one can show [Reference Liero, Mielke and Savaré65, Theorem 7.15] that
![]() $\mathrm {WFR}(\cdot, \cdot )$
metrizes the weak* topology on
$\mathrm {WFR}(\cdot, \cdot )$
metrizes the weak* topology on
![]() $\mathcal {M}(\Omega, \mathbb {R}_+)$
. However, the exact characterisation of the topology induced by a general metric
$\mathcal {M}(\Omega, \mathbb {R}_+)$
. However, the exact characterisation of the topology induced by a general metric
![]() $\mathrm {WB}_{\Lambda }(\cdot, \cdot )$
is still open. In addition, given the multi-component nature of our matrix-valued transport problem, one can expect that there may be some interesting connections between our model
$\mathrm {WB}_{\Lambda }(\cdot, \cdot )$
is still open. In addition, given the multi-component nature of our matrix-valued transport problem, one can expect that there may be some interesting connections between our model
![]() $(\mathcal {M}(\Omega, \mathbb {S}^n_+), \mathrm {WB}_{\Lambda })$
and the multimaterial transport problem [11, 70], which deals with the simultaneous transportation of vector-valued measures along a network or graph and can exhibit the branching behaviour. The detailed investigation of these problems is beyond the scope of this work and left for future work.
$(\mathcal {M}(\Omega, \mathbb {S}^n_+), \mathrm {WB}_{\Lambda })$
and the multimaterial transport problem [11, 70], which deals with the simultaneous transportation of vector-valued measures along a network or graph and can exhibit the branching behaviour. The detailed investigation of these problems is beyond the scope of this work and left for future work.
The proof of Proposition5.2 needs a priori estimates (3.25) and (3.28), and the following lemma, which is a direct consequence of Lemma3.9.
Lemma 5.4.
A subset of
![]() $\mathcal {M}(\Omega, \mathbb {S}^n_+)$
is bounded with respect to the distance
$\mathcal {M}(\Omega, \mathbb {S}^n_+)$
is bounded with respect to the distance
![]() $\mathrm {WB}_\Lambda$
if and only if it is bounded with respect to the total variation norm. Hence, a bounded set in
$\mathrm {WB}_\Lambda$
if and only if it is bounded with respect to the total variation norm. Hence, a bounded set in
![]() $(\mathcal {M}(\Omega, \mathbb {S}^n_+), \mathrm {WB}_\Lambda )$
is weak* relatively compact.
$(\mathcal {M}(\Omega, \mathbb {S}^n_+), \mathrm {WB}_\Lambda )$
is weak* relatively compact.
Proof of Proposition 5.2. First, note that
![]() $\mathrm {WB}_{\Lambda }$
is a function from
$\mathrm {WB}_{\Lambda }$
is a function from
![]() $\mathcal {M}(\Omega, \mathbb {S}^n_+) \times \mathcal {M}(\Omega, \mathbb {S}^n_+)$
to
$\mathcal {M}(\Omega, \mathbb {S}^n_+) \times \mathcal {M}(\Omega, \mathbb {S}^n_+)$
to
![]() $[0,+\infty )$
. It is also easy to check
$[0,+\infty )$
. It is also easy to check
![]() $\mathrm {WB}_{\Lambda }(\mathsf {G}_0,\mathsf {G}_1) = 0$
for
$\mathrm {WB}_{\Lambda }(\mathsf {G}_0,\mathsf {G}_1) = 0$
for
![]() $\mathsf {G}_0 = \mathsf {G}_1$
by considering the constant curve
$\mathsf {G}_0 = \mathsf {G}_1$
by considering the constant curve
![]() $\mathsf {G}_t = \mathsf {G}_0$
with
$\mathsf {G}_t = \mathsf {G}_0$
with
![]() $\mathsf {q} = \mathsf {R} = 0$
, the symmetry
$\mathsf {q} = \mathsf {R} = 0$
, the symmetry
![]() $\mathrm {WB}_{\Lambda }(\mathsf {G}_0,\mathsf {G}_1) = \mathrm {WB}_{\Lambda }(\mathsf {G}_1,\mathsf {G}_0)$
by Lemma3.15 and the triangle inequality by (5.1). Then, to show that
$\mathrm {WB}_{\Lambda }(\mathsf {G}_0,\mathsf {G}_1) = \mathrm {WB}_{\Lambda }(\mathsf {G}_1,\mathsf {G}_0)$
by Lemma3.15 and the triangle inequality by (5.1). Then, to show that
![]() $\mathrm {WB}_{\Lambda }$
is a metric, it suffices to prove that
$\mathrm {WB}_{\Lambda }$
is a metric, it suffices to prove that
![]() $\mathrm {WB}_{\Lambda }(\mathsf {G}_0,\mathsf {G}_1) = 0$
implies
$\mathrm {WB}_{\Lambda }(\mathsf {G}_0,\mathsf {G}_1) = 0$
implies
![]() $\mathsf {G}_0 = \mathsf {G}_1$
.
$\mathsf {G}_0 = \mathsf {G}_1$
.
For this, suppose that
![]() $\mu = \mathsf {(G,q,R)}$
is a minimiser to (
$\mu = \mathsf {(G,q,R)}$
is a minimiser to (
![]() $\mathcal {P}$
) with
$\mathcal {P}$
) with
![]() $\mathcal {J}_{\Lambda, Q}(\mu ) = 0$
. Recalling the formula (3.24), we have
$\mathcal {J}_{\Lambda, Q}(\mu ) = 0$
. Recalling the formula (3.24), we have
![]() $\mathsf {(q,R)} = 0$
. Then, taking test functions
$\mathsf {(q,R)} = 0$
. Then, taking test functions
![]() $\Phi (t,x) = \Psi (x)$
with
$\Phi (t,x) = \Psi (x)$
with
![]() $\Psi (x) \in C^1(\Omega, \mathbb {S}^n)$
in (3.13), we find
$\Psi (x) \in C^1(\Omega, \mathbb {S}^n)$
in (3.13), we find
![]() $\langle \mathsf {G}_1 - \mathsf {G}_0, \Psi \rangle _{\Omega } = 0$
,
$\langle \mathsf {G}_1 - \mathsf {G}_0, \Psi \rangle _{\Omega } = 0$
,
![]() $\forall \Psi \in C^1(\Omega, \mathbb {S}^n)$
, which implies
$\forall \Psi \in C^1(\Omega, \mathbb {S}^n)$
, which implies
![]() $\mathsf {G}_0 = \mathsf {G}_1$
. Next, we show that the metric space
$\mathsf {G}_0 = \mathsf {G}_1$
. Next, we show that the metric space
![]() $(\mathcal {M}(\Omega, \mathbb {S}^n_+), \mathrm {WB}_{\Lambda })$
is complete. Let
$(\mathcal {M}(\Omega, \mathbb {S}^n_+), \mathrm {WB}_{\Lambda })$
is complete. Let
![]() $\{\mathsf {G}^n\}_{n \in \mathbb {N}}$
be a Cauchy sequence in
$\{\mathsf {G}^n\}_{n \in \mathbb {N}}$
be a Cauchy sequence in
![]() $(\mathcal {M}(\Omega, \mathbb {S}^n_+), \mathrm {WB}_{\Lambda })$
, and hence also bounded in
$(\mathcal {M}(\Omega, \mathbb {S}^n_+), \mathrm {WB}_{\Lambda })$
, and hence also bounded in
![]() $\mathrm {WB}_{\Lambda }$
. By Lemma5.4, we have that
$\mathrm {WB}_{\Lambda }$
. By Lemma5.4, we have that
![]() $\mathsf {G}^n$
, up to a subsequence, weak* converges to a measure
$\mathsf {G}^n$
, up to a subsequence, weak* converges to a measure
![]() $\mathsf {G} \in \mathcal {M}(\Omega, \mathbb {S}_+^n)$
. Then, by Corollary4.3 and the fact that
$\mathsf {G} \in \mathcal {M}(\Omega, \mathbb {S}_+^n)$
. Then, by Corollary4.3 and the fact that
![]() $\{\mathsf {G}^n\}$
is a Cauchy sequence, for small
$\{\mathsf {G}^n\}$
is a Cauchy sequence, for small
![]() $\varepsilon \gt 0$
and large enough
$\varepsilon \gt 0$
and large enough
![]() $m$
, there holds
$m$
, there holds
which immediately gives
![]() $\mathrm {WB}_{\Lambda }(\mathsf {G},\mathsf {G}^m) \to 0$
as
$\mathrm {WB}_{\Lambda }(\mathsf {G},\mathsf {G}^m) \to 0$
as
![]() $m \to \infty$
. To finish, we show that
$m \to \infty$
. To finish, we show that
![]() $\mathsf {G}^n$
weak* converges to
$\mathsf {G}^n$
weak* converges to
![]() $\mathsf {G}$
if
$\mathsf {G}$
if
![]() $\mathsf {G}^n$
converges to
$\mathsf {G}^n$
converges to
![]() $\mathsf {G}$
in
$\mathsf {G}$
in
![]() $(\mathcal {M}(\Omega, \mathbb {S}^n_+), \mathrm {WB}_{\Lambda })$
. To do so, it suffices to note that by a similar argument as above, every subsequence of
$(\mathcal {M}(\Omega, \mathbb {S}^n_+), \mathrm {WB}_{\Lambda })$
. To do so, it suffices to note that by a similar argument as above, every subsequence of
![]() $\mathsf {G}^n$
has a weak* convergent sub-subsequence to
$\mathsf {G}^n$
has a weak* convergent sub-subsequence to
![]() $\mathsf {G}$
, which readily gives the weak* convergence of
$\mathsf {G}$
, which readily gives the weak* convergence of
![]() $\mathsf {G}^n$
to
$\mathsf {G}^n$
to
![]() $\mathsf {G}$
.
$\mathsf {G}$
.
The main aim of this section is to show that
![]() $(\mathcal {M}(\Omega, \mathbb {S}^n),\mathrm {WB}_{\Lambda })$
is a geodesic space and then equip it with some differential structure that is consistent with the metric structure, in the spirit of [Reference Ambrosio, Gigli and Savaré1, Reference Dolbeault, Nazaret and Savaré34].
$(\mathcal {M}(\Omega, \mathbb {S}^n),\mathrm {WB}_{\Lambda })$
is a geodesic space and then equip it with some differential structure that is consistent with the metric structure, in the spirit of [Reference Ambrosio, Gigli and Savaré1, Reference Dolbeault, Nazaret and Savaré34].
For the reader’s convenience, we recall some basic concepts for the analysis in metric spaces [Reference Ambrosio and Tilli2]. Let
![]() $(X,d)$
be a metric space and
$(X,d)$
be a metric space and
![]() $\{\omega _t\}_{t \in [a, b]}$
be a curve in
$\{\omega _t\}_{t \in [a, b]}$
be a curve in
![]() $(X,d)$
(i.e., a continuous map from
$(X,d)$
(i.e., a continuous map from
![]() $[a,b]$
to
$[a,b]$
to
![]() $X$
). We say that it is absolutely continuous if there exists a
$X$
). We say that it is absolutely continuous if there exists a
![]() $L^1$
-function
$L^1$
-function
![]() $g$
such that
$g$
such that
![]() $d(\omega _t,\omega _s) \le \int _s^t g(r) \,\mathrm {d} r$
for any
$d(\omega _t,\omega _s) \le \int _s^t g(r) \,\mathrm {d} r$
for any
![]() $a \le s \le t \le b$
. Moreover, the curve is said to have finite
$a \le s \le t \le b$
. Moreover, the curve is said to have finite
![]() $p$
-energy if
$p$
-energy if
![]() $g \in L^p([a,b],\mathbb {R})$
.
$g \in L^p([a,b],\mathbb {R})$
.
The metric derivative
![]() $|\omega _t^{\prime}|$
of
$|\omega _t^{\prime}|$
of
![]() $\{\omega _t\}_{t \in [a, b]}$
at the time point
$\{\omega _t\}_{t \in [a, b]}$
at the time point
![]() $t$
is defined by
$t$
is defined by
![]() $|\omega^{\prime}_t| \,:\!=\, \lim _{\delta \to 0}|\delta |^{-1} d(\omega _{t + \delta },\omega _t)$
, if the limit exists. It can be shown [Reference Ambrosio, Gigli and Savaré1, Theorem 1.1.2] that for an absolutely continuous curve
$|\omega^{\prime}_t| \,:\!=\, \lim _{\delta \to 0}|\delta |^{-1} d(\omega _{t + \delta },\omega _t)$
, if the limit exists. It can be shown [Reference Ambrosio, Gigli and Savaré1, Theorem 1.1.2] that for an absolutely continuous curve
![]() $\omega _t$
, the metric derivative
$\omega _t$
, the metric derivative
![]() $|\omega^{\prime}_t|$
is well-defined for a.e.
$|\omega^{\prime}_t|$
is well-defined for a.e.
![]() $t \in [a,b]$
and satisfies
$t \in [a,b]$
and satisfies
![]() $|\omega^{\prime}_t| \le g(t)$
.
$|\omega^{\prime}_t| \le g(t)$
.
The length
![]() $\mathrm {L}(\omega _t)$
of an absolutely continuous curve
$\mathrm {L}(\omega _t)$
of an absolutely continuous curve
![]() $\{\omega _t\}_{t \in [a,b]}$
is defined as
$\{\omega _t\}_{t \in [a,b]}$
is defined as
![]() $\mathrm { L}(\omega _t) = \int _a^b |\omega^{\prime}_t| \,\mathrm {d} t$
, which is invariant with respect to the reparameterisation. Then,
$\mathrm { L}(\omega _t) = \int _a^b |\omega^{\prime}_t| \,\mathrm {d} t$
, which is invariant with respect to the reparameterisation. Then,
![]() $(X,d)$
is a geodesic space if for any
$(X,d)$
is a geodesic space if for any
![]() $x,y \in X$
, there holds
$x,y \in X$
, there holds
where the minimiser exists and is called the (minimizing) geodesic between
![]() $x$
and
$x$
and
![]() $y$
. Recall [Reference Ambrosio, Gigli and Savaré1, Lemma 1.1.4] that any absolutely continuous curve can be reparameterised as a Lipschitz one with constant metric derivative
$y$
. Recall [Reference Ambrosio, Gigli and Savaré1, Lemma 1.1.4] that any absolutely continuous curve can be reparameterised as a Lipschitz one with constant metric derivative
![]() $|\omega^{\prime}_t| = \mathrm {L}(\omega _t)$
a.e.. Hence, we can always assume that the geodesic is constant-speed (i.e.,
$|\omega^{\prime}_t| = \mathrm {L}(\omega _t)$
a.e.. Hence, we can always assume that the geodesic is constant-speed (i.e.,
![]() $|\omega _t^{\prime}|$
is constant a.e.). Then, it is clear from definition (5.3) that a curve
$|\omega _t^{\prime}|$
is constant a.e.). Then, it is clear from definition (5.3) that a curve
![]() $\{\omega _t\}_{t \in [0,1]}$
is a constant-speed geodesic if and only if it satisfies
$\{\omega _t\}_{t \in [0,1]}$
is a constant-speed geodesic if and only if it satisfies
![]() $d(\omega _s,\omega _t) = |t -s |d (\omega _0,\omega _1)$
for any
$d(\omega _s,\omega _t) = |t -s |d (\omega _0,\omega _1)$
for any
![]() $0 \lt s \lt t \lt 1$
.
$0 \lt s \lt t \lt 1$
.
From the above concepts, we see that for our purpose, a key step is to characterise the absolutely continuous curves in the metric space
![]() $(\mathcal {M}(\Omega, \mathbb {S}^n_+),\mathrm {WB}_{\Lambda })$
, which is given by the following theorem extended from [Reference Dolbeault, Nazaret and Savaré34, Theorem 5.17].
$(\mathcal {M}(\Omega, \mathbb {S}^n_+),\mathrm {WB}_{\Lambda })$
, which is given by the following theorem extended from [Reference Dolbeault, Nazaret and Savaré34, Theorem 5.17].
Theorem 5.5.
A curve
![]() $\{\mathsf {G}_t\}_{t \in [a,b]}$
,
$\{\mathsf {G}_t\}_{t \in [a,b]}$
,
![]() $b \gt a \gt 0$
, is absolutely continuous with respect to the metric
$b \gt a \gt 0$
, is absolutely continuous with respect to the metric
![]() $\mathrm {WB}_{\Lambda }$
if and only if there exists
$\mathrm {WB}_{\Lambda }$
if and only if there exists
![]() $(\mathsf {q},\mathsf {R}) \in \mathcal {M}(Q,\mathbb {R}^{n \times k} \times \mathbb {M}^n)$
such that
$(\mathsf {q},\mathsf {R}) \in \mathcal {M}(Q,\mathbb {R}^{n \times k} \times \mathbb {M}^n)$
such that
![]() $\mu = (\mathsf {G},\mathsf {q},\mathsf {R}) \in \widetilde {\mathcal {CE}}([a,b];\mathsf {G}_0,\mathsf {G}_1)$
and
$\mu = (\mathsf {G},\mathsf {q},\mathsf {R}) \in \widetilde {\mathcal {CE}}([a,b];\mathsf {G}_0,\mathsf {G}_1)$
and
In this case, the metric derivative
![]() $|\mathsf {G}_t^{\prime}|$
satisfies
$|\mathsf {G}_t^{\prime}|$
satisfies
and there exists unique
![]() $(\mathsf {q}_{*}, \mathsf {R}_{*})$
such that the equality in (
5.5
) holds a.e., where the uniqueness is in the sense of equivalence class:
$(\mathsf {q}_{*}, \mathsf {R}_{*})$
such that the equality in (
5.5
) holds a.e., where the uniqueness is in the sense of equivalence class:
![]() $\mathsf {(q,R)} \sim (\mathsf {q}^{\prime},\mathsf {R}^{\prime})$
if and only if
$\mathsf {(q,R)} \sim (\mathsf {q}^{\prime},\mathsf {R}^{\prime})$
if and only if
![]() $\mathcal {J}_{\Lambda, Q_a^b}((\mathsf {G}, \mathsf {q-q}^{\prime},\mathsf {R-R}^{\prime})) = 0$
. If
$\mathcal {J}_{\Lambda, Q_a^b}((\mathsf {G}, \mathsf {q-q}^{\prime},\mathsf {R-R}^{\prime})) = 0$
. If
![]() $\mathsf {G}_t$
has finite
$\mathsf {G}_t$
has finite
![]() $2$
-energy, then
$2$
-energy, then
![]() $(\mathsf {q}_{*}, \mathsf {R}_{*}) = (\mathsf {G}u_*, \mathsf {G}W_*)$
with the
$(\mathsf {q}_{*}, \mathsf {R}_{*}) = (\mathsf {G}u_*, \mathsf {G}W_*)$
with the
![]() $L^2_{\mathsf {G},\Lambda }$
-field
$L^2_{\mathsf {G},\Lambda }$
-field
![]() $(u_*,W_*)$
given in Theorem 4.5
.
$(u_*,W_*)$
given in Theorem 4.5
.
Remark 5.6. As a corollary of Theorem 5.5, we have that
![]() $\mathcal {AC}([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
in (4.15) is nothing else than the set of absolutely continuous curves with finite
$\mathcal {AC}([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
in (4.15) is nothing else than the set of absolutely continuous curves with finite
![]() $2$
-energy.
$2$
-energy.
Proof. It suffices to consider the case
![]() $[a,b] = [0,1]$
. We first consider the trivial if part. For
$[a,b] = [0,1]$
. We first consider the trivial if part. For
![]() $\mu \in \widetilde {\mathcal {CE}}([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
with the property (5.4), it follows from (5.1) that
$\mu \in \widetilde {\mathcal {CE}}([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
with the property (5.4), it follows from (5.1) that
which, by definition, readily implies that
![]() $\{\mathsf {G}_t\}_{t \in [0,1]}$
is absolutely continuous and (5.5) holds. We now consider the only if part. Let
$\{\mathsf {G}_t\}_{t \in [0,1]}$
is absolutely continuous and (5.5) holds. We now consider the only if part. Let
![]() $\{\mathsf {G}_t\}_{t \in [0,1]}$
be an absolutely continuous curve, which, by reparameterisation, can be further assumed to be Lipschitz with the Lipschitz constant denoted by
$\{\mathsf {G}_t\}_{t \in [0,1]}$
be an absolutely continuous curve, which, by reparameterisation, can be further assumed to be Lipschitz with the Lipschitz constant denoted by
![]() $\mathrm {Lip}(\mathsf {G}_t)$
. We will approximate it by piecewise constant-speed curves. We fix an integer
$\mathrm {Lip}(\mathsf {G}_t)$
. We will approximate it by piecewise constant-speed curves. We fix an integer
![]() $N \in \mathbb {N}$
with the step size
$N \in \mathbb {N}$
with the step size
![]() $\tau = 2^{-N}$
. Let
$\tau = 2^{-N}$
. Let
![]() $\{\mu _t^{k,N}\}_{t \in [(k-1)\tau, k \tau ]}$
be a minimiser to (
$\{\mu _t^{k,N}\}_{t \in [(k-1)\tau, k \tau ]}$
be a minimiser to (
![]() $\mathcal {P}^{\prime}$
) with
$\mathcal {P}^{\prime}$
) with
![]() $[a,b] = [(k - 1)\tau, k \tau ]$
, which satisfies
$[a,b] = [(k - 1)\tau, k \tau ]$
, which satisfies
by Lemma5.1 and the absolute continuity of
![]() $\mathsf {G}_t$
. We glue the curves
$\mathsf {G}_t$
. We glue the curves
![]() $\big \{\mu ^{k,N}_t\big \}_{t \in [(k-1)\tau, k\tau ]}$
with
$\big \{\mu ^{k,N}_t\big \}_{t \in [(k-1)\tau, k\tau ]}$
with
![]() $k = 1,\ldots, 2^N$
and obtain a new one
$k = 1,\ldots, 2^N$
and obtain a new one
![]() $\{\mu ^N_t = (\mathsf {G}_t^N,\mathsf {q}_t^N,\mathsf {R}_t^N)\}_{t \in [0,1]} \in \mathcal {CE}_\infty ([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
.
$\{\mu ^N_t = (\mathsf {G}_t^N,\mathsf {q}_t^N,\mathsf {R}_t^N)\}_{t \in [0,1]} \in \mathcal {CE}_\infty ([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
.
Next, note that for any
![]() $(a,b) \subset [0,1]$
, there exists
$(a,b) \subset [0,1]$
, there exists
![]() $k_1^N, k_2^N \in \mathbb {N}$
with
$k_1^N, k_2^N \in \mathbb {N}$
with
![]() $N$
large enough such that
$N$
large enough such that
![]() $[(k^N_1 + 1)\tau, (k_2^N - 1) \tau ] \subset (a,b) \subset [k^N_1 \tau, k_2^N \tau ]$
. By squaring (5.6) and summing it from
$[(k^N_1 + 1)\tau, (k_2^N - 1) \tau ] \subset (a,b) \subset [k^N_1 \tau, k_2^N \tau ]$
. By squaring (5.6) and summing it from
![]() $k = k_1^N + 1$
to
$k = k_1^N + 1$
to
![]() $ k = k_2^N$
, there holds
$ k = k_2^N$
, there holds
 \begin{align} \int _a^b \mathcal {J}_{\Lambda, \Omega }(\mu _t^N)\, \mathrm {d} t \le \sum _{k = k^N_1 + 1}^{k^N_2} \int _{(k-1)\tau }^{k\tau } \mathcal {J}_{\Lambda, \Omega }(\mu ^{k, N}_t)\, \mathrm {d} t\le \int _{a}^{b} |\mathsf {G}_t^{\prime}|^2\, \mathrm {d} t + 2 \tau \mathrm {Lip}(\mathsf {G}_t)^2\,. \end{align}
\begin{align} \int _a^b \mathcal {J}_{\Lambda, \Omega }(\mu _t^N)\, \mathrm {d} t \le \sum _{k = k^N_1 + 1}^{k^N_2} \int _{(k-1)\tau }^{k\tau } \mathcal {J}_{\Lambda, \Omega }(\mu ^{k, N}_t)\, \mathrm {d} t\le \int _{a}^{b} |\mathsf {G}_t^{\prime}|^2\, \mathrm {d} t + 2 \tau \mathrm {Lip}(\mathsf {G}_t)^2\,. \end{align}
By taking
![]() $a = 0$
,
$a = 0$
,
![]() $b = 1$
in (5.7), we observe that
$b = 1$
in (5.7), we observe that
![]() $\int _0^1 \mathcal {J}_{\Lambda, \Omega }(\mu _t^N) \,\mathrm {d} t$
is uniformly bounded in
$\int _0^1 \mathcal {J}_{\Lambda, \Omega }(\mu _t^N) \,\mathrm {d} t$
is uniformly bounded in
![]() $N$
. By Proposition3.18, up to a subsequence,
$N$
. By Proposition3.18, up to a subsequence,
![]() $\{\mu ^N_t\}_{t \in [0,1]}$
weak* converges to a measure
$\{\mu ^N_t\}_{t \in [0,1]}$
weak* converges to a measure
![]() $\widetilde {\mu } = (\widetilde {\mathsf {G}},\widetilde {\mathsf {q}},\widetilde {\mathsf {R}}) \in \mathcal {CE}_\infty ([0,1],\mathsf {G}_0,\mathsf {G}_1)$
. Moreover, it follows from (3.38) and (5.7) that, for
$\widetilde {\mu } = (\widetilde {\mathsf {G}},\widetilde {\mathsf {q}},\widetilde {\mathsf {R}}) \in \mathcal {CE}_\infty ([0,1],\mathsf {G}_0,\mathsf {G}_1)$
. Moreover, it follows from (3.38) and (5.7) that, for
![]() $[a,b] \subset [0,1]$
,
$[a,b] \subset [0,1]$
,
We now show
![]() $\widetilde {\mathsf {G}}_t = \mathsf {G}_t$
for
$\widetilde {\mathsf {G}}_t = \mathsf {G}_t$
for
![]() $0 \le t \le 1$
. Note that for any
$0 \le t \le 1$
. Note that for any
![]() $t \in [0,1]$
, there exists a sequence of integers
$t \in [0,1]$
, there exists a sequence of integers
![]() $k_N$
such that
$k_N$
such that
![]() $s_N = k_N 2^{-N} \to t$
as
$s_N = k_N 2^{-N} \to t$
as
![]() $N \to \infty$
, which implies that
$N \to \infty$
, which implies that
![]() $\mathsf {G}^N_{s_N} = \mathsf {G}_{s_N}$
weak* converges to
$\mathsf {G}^N_{s_N} = \mathsf {G}_{s_N}$
weak* converges to
![]() $\widetilde {\mathsf {G}}_t$
by Proposition3.18. Meanwhile,
$\widetilde {\mathsf {G}}_t$
by Proposition3.18. Meanwhile,
![]() $\mathsf {G}_{s_N}$
weak* converges to
$\mathsf {G}_{s_N}$
weak* converges to
![]() $\mathsf {G}_t$
by the continuity of
$\mathsf {G}_t$
by the continuity of
![]() $\mathsf {G}_t$
. We hence have
$\mathsf {G}_t$
. We hence have
![]() $\widetilde {\mathsf {G}}_t = \mathsf {G}_t$
. Then, it follows from (5.8) that
$\widetilde {\mathsf {G}}_t = \mathsf {G}_t$
. Then, it follows from (5.8) that
by Lebesgue differentiation theorem. The proof of the only if direction is completed by noting that (5.4) and (5.5) are invariant with respect to the parameterisation. The uniqueness of
![]() $(\mathsf {q}_*, \mathsf {R}_*)$
follows from the linearity of the continuity equation in the variable
$(\mathsf {q}_*, \mathsf {R}_*)$
follows from the linearity of the continuity equation in the variable
![]() $(\mathsf {q},\mathsf {R})$
and the strict convexity of the
$(\mathsf {q},\mathsf {R})$
and the strict convexity of the
![]() $L^2_{\mathsf {G}}$
-norm.
$L^2_{\mathsf {G}}$
-norm.
We finally show that when
![]() $\mathsf {G}_t$
is absolutely continuous with finite
$\mathsf {G}_t$
is absolutely continuous with finite
![]() $2$
-energy,
$2$
-energy,
![]() $\mu \,:\!=\, (\mathsf {G}, \mathsf {G}u_{*}, \mathsf {G}W_{*}) \in \mathcal{CE}_{\infty} ([0,1];\,\mathsf{G}_0,\mathsf{G}_1)$
satisfies
$\mu \,:\!=\, (\mathsf {G}, \mathsf {G}u_{*}, \mathsf {G}W_{*}) \in \mathcal{CE}_{\infty} ([0,1];\,\mathsf{G}_0,\mathsf{G}_1)$
satisfies
![]() $\mathcal {J}_{\Lambda, \Omega }(\mu _t)^{1/2} \le |\mathsf {G}_t^{\prime}|$
for a.e.
$\mathcal {J}_{\Lambda, \Omega }(\mu _t)^{1/2} \le |\mathsf {G}_t^{\prime}|$
for a.e.
![]() $t \in [0,1]$
, where
$t \in [0,1]$
, where
![]() $(u_*,W_*)$
is given in Theorem4.5 (i.e., the Riesz representation of
$(u_*,W_*)$
is given in Theorem4.5 (i.e., the Riesz representation of
![]() $\widetilde {l}_{\mathsf {G}}$
in
$\widetilde {l}_{\mathsf {G}}$
in
![]() $H_{\mathsf {G},\Lambda }(\mathsf {D}^*)$
). Let
$H_{\mathsf {G},\Lambda }(\mathsf {D}^*)$
). Let
![]() $(a,b) \subset [0,1]$
, and
$(a,b) \subset [0,1]$
, and
![]() $\eta \in C_c^\infty ((a,b))$
with
$\eta \in C_c^\infty ((a,b))$
with
![]() $0 \le \eta \le 1$
, and
$0 \le \eta \le 1$
, and
![]() $\{(\mathsf {D}^* \Phi _n \Lambda _1^2, \Phi _n \Lambda _2^2)\}$
with
$\{(\mathsf {D}^* \Phi _n \Lambda _1^2, \Phi _n \Lambda _2^2)\}$
with
![]() $\Phi _n \in C^1(Q,\mathbb {S}^n)$
be a sequence approximating
$\Phi _n \in C^1(Q,\mathbb {S}^n)$
be a sequence approximating
![]() $(u_*, W_*)$
. Then, by using (4.18) and noting
$(u_*, W_*)$
. Then, by using (4.18) and noting
![]() $\mathsf {D}^* (\eta ^2 \Phi ) = \eta ^2 \mathsf {D}^* (\Phi )$
, we have
$\mathsf {D}^* (\eta ^2 \Phi ) = \eta ^2 \mathsf {D}^* (\Phi )$
, we have
By only if part proved above, there exists some
![]() $\mathsf {(q,R)}$
such that
$\mathsf {(q,R)}$
such that
 \begin{align} \left |l_{\mathsf {G}}(\eta ^2 \Phi _n)\right | &\le \left \lVert (G^\dagger q, G^\dagger R) \right \rVert _{L^2_{\mathsf {G},\Lambda }(Q_a^b)} \left \lVert (\mathsf {D}^* \eta ^2 \Phi _n, \eta ^2 \Phi _n) \right \rVert _{L^2_{\mathsf {G},\Lambda }(Q_a^b)}\notag \\ & \le \Big (\int _a^b |\mathsf {G}_t^{\prime}|^2 \, \mathrm {d} t \Big )^{1/2} \left \lVert ( \mathsf {D}^* \Phi _n, \Phi _n) \right \rVert _{L^2_{\mathsf {G},\Lambda }(Q_a^b)}\,. \end{align}
\begin{align} \left |l_{\mathsf {G}}(\eta ^2 \Phi _n)\right | &\le \left \lVert (G^\dagger q, G^\dagger R) \right \rVert _{L^2_{\mathsf {G},\Lambda }(Q_a^b)} \left \lVert (\mathsf {D}^* \eta ^2 \Phi _n, \eta ^2 \Phi _n) \right \rVert _{L^2_{\mathsf {G},\Lambda }(Q_a^b)}\notag \\ & \le \Big (\int _a^b |\mathsf {G}_t^{\prime}|^2 \, \mathrm {d} t \Big )^{1/2} \left \lVert ( \mathsf {D}^* \Phi _n, \Phi _n) \right \rVert _{L^2_{\mathsf {G},\Lambda }(Q_a^b)}\,. \end{align}
Combining (5.9) with (5.10) and letting
![]() $\eta$
approximate
$\eta$
approximate
![]() $\chi _{[a,b]}$
, we obtain
$\chi _{[a,b]}$
, we obtain
Then, by Lebesgue differentiation theorem again, the inequality (5.11) gives the desired
![]() $\mathcal {J}_{\Lambda, \Omega }(\mu _t)^{1/2} \le |\mathsf {G}_t^{\prime}|$
for the measure
$\mathcal {J}_{\Lambda, \Omega }(\mu _t)^{1/2} \le |\mathsf {G}_t^{\prime}|$
for the measure
![]() $\mu = (\mathsf {G}, \mathsf {G}u_*, \mathsf {G}W_*)$
. The proof is complete.
$\mu = (\mathsf {G}, \mathsf {G}u_*, \mathsf {G}W_*)$
. The proof is complete.
From Lemma5.1 and Theorem5.5, we have
 \begin{align} \mathrm {WB}_\Lambda (\mathsf {G}_0,\mathsf {G}_1) & = \inf _{\mathsf {G}} \inf _{\mathsf {(q,R)}} \Big \{\int _0^1 \mathcal {J}_{\Lambda, \Omega }(\mu _t)^{1/2} \,\mathrm {d} t\,;\ \mu = \mathsf {(G,q,R)} \in \widetilde {\mathcal {CE}}([0,1];\,\mathsf {G}_0,\mathsf {G}_1) \Big \}\notag \\ & = \inf _{\mathsf {G}} \Big \{ \int _0^1 |\mathsf {G}_t^{\prime}| \, \mathrm {d} t\,; \ \{\mathsf {G}\}_{t \in [0,1]} \ \text {is absolutely continuous with}\ \mathsf {G}_t|_{t = 0} = \mathsf {G}_0\,, \mathsf {G}_t|_{t = 1} = \mathsf {G}_1 \Big \}\,. \end{align}
\begin{align} \mathrm {WB}_\Lambda (\mathsf {G}_0,\mathsf {G}_1) & = \inf _{\mathsf {G}} \inf _{\mathsf {(q,R)}} \Big \{\int _0^1 \mathcal {J}_{\Lambda, \Omega }(\mu _t)^{1/2} \,\mathrm {d} t\,;\ \mu = \mathsf {(G,q,R)} \in \widetilde {\mathcal {CE}}([0,1];\,\mathsf {G}_0,\mathsf {G}_1) \Big \}\notag \\ & = \inf _{\mathsf {G}} \Big \{ \int _0^1 |\mathsf {G}_t^{\prime}| \, \mathrm {d} t\,; \ \{\mathsf {G}\}_{t \in [0,1]} \ \text {is absolutely continuous with}\ \mathsf {G}_t|_{t = 0} = \mathsf {G}_0\,, \mathsf {G}_t|_{t = 1} = \mathsf {G}_1 \Big \}\,. \end{align}
Note that if
![]() $\{\mu _t\}_{t \in [0,1]} \in \mathcal {CE}_\infty ([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
minimises (
$\{\mu _t\}_{t \in [0,1]} \in \mathcal {CE}_\infty ([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
minimises (
![]() $\mathcal {P}$
), then for any
$\mathcal {P}$
), then for any
![]() $0 \le a \lt b \le 1$
,
$0 \le a \lt b \le 1$
,
![]() $\{\mu _t\}_{t \in [a,b]}$
is a minimiser to (
$\{\mu _t\}_{t \in [a,b]}$
is a minimiser to (
![]() $\mathcal {P}^{\prime}$
) with
$\mathcal {P}^{\prime}$
) with
![]() $\mathsf {G}_0 = \mathsf {G}_t|_{t = a}$
and
$\mathsf {G}_0 = \mathsf {G}_t|_{t = a}$
and
![]() $\mathsf {G}_1 = \mathsf {G}_t|_{t = b}$
. Recalling the constant-speed property (5.2) of the minimiser
$\mathsf {G}_1 = \mathsf {G}_t|_{t = b}$
. Recalling the constant-speed property (5.2) of the minimiser
![]() $\mu = \mathsf {(G,q,R)}$
, we readily see that the associated
$\mu = \mathsf {(G,q,R)}$
, we readily see that the associated
![]() $\{\mathsf {G}_t\}_{t \in [0,1]}$
is the desired constant-speed geodesic:
$\{\mathsf {G}_t\}_{t \in [0,1]}$
is the desired constant-speed geodesic:
It allows us to conclude that the
![]() $\inf$
in (5.12) is attained, and the main result follows.
$\inf$
in (5.12) is attained, and the main result follows.
Corollary 5.7.
![]() $(\mathcal {M}(\Omega, \mathbb {S}^n_+), \mathrm {WB}_{\Lambda })$
is a geodesic space. The constant-speed geodesic connecting
$(\mathcal {M}(\Omega, \mathbb {S}^n_+), \mathrm {WB}_{\Lambda })$
is a geodesic space. The constant-speed geodesic connecting
![]() $\mathsf {G}_0, \mathsf {G}_1 \in \mathcal {M}(\Omega, \mathbb {S}^n_+)$
is given by the minimiser to (
$\mathsf {G}_0, \mathsf {G}_1 \in \mathcal {M}(\Omega, \mathbb {S}^n_+)$
is given by the minimiser to (
![]() $\mathcal {P}$
).
$\mathcal {P}$
).
Another important application of Theorem5.5 is that we can view the set of
![]() $\mathbb {S}^n_+$
-valued measures as a pseudo-Riemannian manifold, following [Reference Ambrosio, Gigli and Savaré1, Proposition 8.4.5]. We define the tangent space at each
$\mathbb {S}^n_+$
-valued measures as a pseudo-Riemannian manifold, following [Reference Ambrosio, Gigli and Savaré1, Proposition 8.4.5]. We define the tangent space at each
![]() $\mathsf {G} \in \mathcal {M}(\Omega, \mathbb {S}_+^n)$
by
$\mathsf {G} \in \mathcal {M}(\Omega, \mathbb {S}_+^n)$
by
From Theorem5.5, we have that among all the measures
![]() $\mathsf {(q,R)}$
generating
$\mathsf {(q,R)}$
generating
![]() $\{\mathsf {G}_t\}_{t \in [0,1]}$
by the continuity equation, there is a unique one
$\{\mathsf {G}_t\}_{t \in [0,1]}$
by the continuity equation, there is a unique one
![]() $(\mathsf {q}_*, \mathsf {R}_*)$
with minimal
$(\mathsf {q}_*, \mathsf {R}_*)$
with minimal
![]() $\mathcal {J}_{\Lambda, \Omega }(\mu _t)$
given by
$\mathcal {J}_{\Lambda, \Omega }(\mu _t)$
given by
![]() $|\mathsf {G}_t^{\prime}|$
for a.e.
$|\mathsf {G}_t^{\prime}|$
for a.e.
![]() $t \in [0,1]$
, that is,
$t \in [0,1]$
, that is,
![]() $(\mathsf {q}_{*,t},\mathsf {R}_{*,t}) \in Tan(\mathsf {G}_t)$
a.e. by (5.14). We also introduce the space
$(\mathsf {q}_{*,t},\mathsf {R}_{*,t}) \in Tan(\mathsf {G}_t)$
a.e. by (5.14). We also introduce the space
![]() $Tan_{field}(\mathsf {G})$
similar to
$Tan_{field}(\mathsf {G})$
similar to
![]() $H_{\mathsf {G},\Lambda }(\mathsf {D}^*)$
(4.20):
$H_{\mathsf {G},\Lambda }(\mathsf {D}^*)$
(4.20):
Then, similarly to the argument for Theorem4.5, the tangent space
![]() $Tan(\mathsf {G})$
can be characterised as follows:
$Tan(\mathsf {G})$
can be characterised as follows:
We summarise the above discussions in the following corollary, which provides a Riemannian interpretation of the transport distance
![]() $\mathrm {WB}_\Lambda (\cdot, \cdot )$
.
$\mathrm {WB}_\Lambda (\cdot, \cdot )$
.
Corollary 5.8.
Let
![]() $\{\mathsf {G}_t\}_{t \in [0,1]}$
be an absolutely continuous curve in
$\{\mathsf {G}_t\}_{t \in [0,1]}$
be an absolutely continuous curve in
![]() $(\mathcal {M}(\Omega, \mathbb {S}_+^n),\mathrm {WB}_\Lambda )$
and
$(\mathcal {M}(\Omega, \mathbb {S}_+^n),\mathrm {WB}_\Lambda )$
and
![]() $\{(\mathsf {q}_t,\mathsf {R}_t)\}_{t \in [0,1]}$
be the family of measures in
$\{(\mathsf {q}_t,\mathsf {R}_t)\}_{t \in [0,1]}$
be the family of measures in
![]() $\mathcal {M}(\Omega, \mathbb {R}^{n \times k} \times \mathbb {M}^n)$
such that
$\mathcal {M}(\Omega, \mathbb {R}^{n \times k} \times \mathbb {M}^n)$
such that
![]() $\mu = (\mathsf {G},\mathsf {q},\mathsf {R}) \in \mathcal {CE} ([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
and
$\mu = (\mathsf {G},\mathsf {q},\mathsf {R}) \in \mathcal {CE} ([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
and
![]() $ \mathcal {J}_{\Lambda, \Omega }(\mu _t)$
is finite a.e.. Then
$ \mathcal {J}_{\Lambda, \Omega }(\mu _t)$
is finite a.e.. Then
![]() $|\mathsf {G}_t^{\prime}| = \mathcal {J}_{\Lambda, \Omega }(\mu _t)$
holds for a.e.
$|\mathsf {G}_t^{\prime}| = \mathcal {J}_{\Lambda, \Omega }(\mu _t)$
holds for a.e.
![]() $t \in [0,1]$
if and only if
$t \in [0,1]$
if and only if
![]() $(\mathsf {q}_t, \mathsf {R}_t) \in Tan(\mathsf {G}_t)$
a.e., where
$(\mathsf {q}_t, \mathsf {R}_t) \in Tan(\mathsf {G}_t)$
a.e., where
![]() $Tan(\mathsf {G})$
is defined in (5.14) and characterised by (5.15). Moreover, for absolutely continuous
$Tan(\mathsf {G})$
is defined in (5.14) and characterised by (5.15). Moreover, for absolutely continuous
![]() $\mathsf {G}_t$
with finite 2-energy (i.e.,
$\mathsf {G}_t$
with finite 2-energy (i.e.,
![]() $\mathsf {G} \in \mathcal {AC}([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
), let
$\mathsf {G} \in \mathcal {AC}([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
), let
![]() $(u_*,W_*)$
be the unique minimiser to (4.22). Then, there holds
$(u_*,W_*)$
be the unique minimiser to (4.22). Then, there holds
![]() $(u_{*,t},W_{*,t}) \in Tan_{field}(\mathsf {G}_t)$
a.e..
$(u_{*,t},W_{*,t}) \in Tan_{field}(\mathsf {G}_t)$
a.e..
6. Cone space and spherical distance
In this section, we discuss the conic structure of our weighted transport distance
![]() $\mathrm {WB}_\Lambda$
, which extends the results in [Reference Brenier and Vorotnikov16, Section 4] and [Reference Monsaingeon and Vorotnikov73, Section 5]. The starting point is a spherical distance associated with
$\mathrm {WB}_\Lambda$
, which extends the results in [Reference Brenier and Vorotnikov16, Section 4] and [Reference Monsaingeon and Vorotnikov73, Section 5]. The starting point is a spherical distance associated with
![]() $\mathrm {WB}_\Lambda$
:
$\mathrm {WB}_\Lambda$
:
where
![]() $Tr_\Lambda (X) \,:\!=\, Tr\big (\widetilde {\Lambda }_2^{-1}X\widetilde {\Lambda }_2^{-1}\big )$
with
$Tr_\Lambda (X) \,:\!=\, Tr\big (\widetilde {\Lambda }_2^{-1}X\widetilde {\Lambda }_2^{-1}\big )$
with
![]() $\widetilde {\Lambda }_2 = n \Lambda _2/Tr(\Lambda _2)$
is the scaled trace and
$\widetilde {\Lambda }_2 = n \Lambda _2/Tr(\Lambda _2)$
is the scaled trace and
We will prove that
![]() $(\mathcal {M}_1, \mathrm {SWB}_{\Lambda })$
is a complete geodesic space and
$(\mathcal {M}_1, \mathrm {SWB}_{\Lambda })$
is a complete geodesic space and
![]() $(\mathcal {M}(\Omega, \mathbb {S}_+^n),\mathrm {WB}_\Lambda )$
can be viewed as its metric cone. Let us first recall some basic concepts [Reference Burago, Burago and Ivanov19, Reference Laschos and Mielke60]. We consider a metric space
$(\mathcal {M}(\Omega, \mathbb {S}_+^n),\mathrm {WB}_\Lambda )$
can be viewed as its metric cone. Let us first recall some basic concepts [Reference Burago, Burago and Ivanov19, Reference Laschos and Mielke60]. We consider a metric space
![]() $(X,d_X)$
with diameter
$(X,d_X)$
with diameter
![]() $\mathrm {diam}(X) = \sup _{x,y\in X}d_X(x,y) \le \pi$
. The associated cone is defined by
$\mathrm {diam}(X) = \sup _{x,y\in X}d_X(x,y) \le \pi$
. The associated cone is defined by
![]() $\mathfrak {C}(X) \,:\!=\, X \times [0,\infty ) \backslash X \times \{0\}$
with the metric
$\mathfrak {C}(X) \,:\!=\, X \times [0,\infty ) \backslash X \times \{0\}$
with the metric
where a point in
![]() $\mathfrak {C}(X)$
is of the form
$\mathfrak {C}(X)$
is of the form
![]() $[x,r]$
with
$[x,r]$
with
![]() $x \in X$
and
$x \in X$
and
![]() $r \ge 0$
and satisfies the equivalence relation
$r \ge 0$
and satisfies the equivalence relation
![]() $[x_0,0] \sim [x_1,0]$
. It can be proved that for
$[x_0,0] \sim [x_1,0]$
. It can be proved that for
![]() $x_0, x_1 \in X$
with
$x_0, x_1 \in X$
with
![]() $0 \lt d_X(x_0, x_1) \lt \pi$
and
$0 \lt d_X(x_0, x_1) \lt \pi$
and
![]() $r_0,r_1 \gt 0$
, there is one-to-one correspondence between the geodesics for
$r_0,r_1 \gt 0$
, there is one-to-one correspondence between the geodesics for
![]() $d_{\mathfrak {C}(X)}([x_0,r_0],[x_1,r_1])$
and for
$d_{\mathfrak {C}(X)}([x_0,r_0],[x_1,r_1])$
and for
![]() $d_{X}(x_0,x_1)$
; see [Reference Laschos and Mielke60, Theorem 2.6]. In particular, we have the following useful lemmas from [Reference Brenier and Vorotnikov16, Lemma 4.4] and [Reference Laschos and Mielke60, Theorem 2.2], respectively.
$d_{X}(x_0,x_1)$
; see [Reference Laschos and Mielke60, Theorem 2.6]. In particular, we have the following useful lemmas from [Reference Brenier and Vorotnikov16, Lemma 4.4] and [Reference Laschos and Mielke60, Theorem 2.2], respectively.
Lemma 6.1.
If
![]() $X$
is a length space, then the distance
$X$
is a length space, then the distance
![]() $d_X(x_0,x_1)$
can be characterised by
$d_X(x_0,x_1)$
can be characterised by
where
![]() $|[x_t,1]^{\prime}|_{\mathfrak {C}(X)}$
is the metric derivative in the space
$|[x_t,1]^{\prime}|_{\mathfrak {C}(X)}$
is the metric derivative in the space
![]() $(\mathfrak {C}(X),d_{\mathfrak {C}(X)})$
.
$(\mathfrak {C}(X),d_{\mathfrak {C}(X)})$
.
Lemma 6.2.
Let
![]() $\mathfrak {C}(X)$
be the cone as above and
$\mathfrak {C}(X)$
be the cone as above and
![]() $(\mathfrak {C}(X), d)$
be a metric space for some metric
$(\mathfrak {C}(X), d)$
be a metric space for some metric
![]() $d$
. If there holds
$d$
. If there holds
and
![]() $0 \lt d^2([x_0,1],[x_1,1]) \le 4$
for
$0 \lt d^2([x_0,1],[x_1,1]) \le 4$
for
![]() $x_0 \neq x_1$
, then
$x_0 \neq x_1$
, then
![]() $d_X(x_0,x_1)\,:\!=\, \arccos (1 - d^2([x_0,1], [x_1, 1])/2)$
is a metric on
$d_X(x_0,x_1)\,:\!=\, \arccos (1 - d^2([x_0,1], [x_1, 1])/2)$
is a metric on
![]() $X$
such that
(6.3)
holds, equivalently,
$X$
such that
(6.3)
holds, equivalently,
![]() $(\mathfrak {C}(X), d)$
is a metric cone over
$(\mathfrak {C}(X), d)$
is a metric cone over
![]() $(X,d_X)$
.
$(X,d_X)$
.
We are now ready to consider the conic properties of
![]() $(\mathcal {M}(\Omega, \mathbb {S}^n_+), \mathrm {WB}_{\Lambda })$
. For this, we set
$(\mathcal {M}(\Omega, \mathbb {S}^n_+), \mathrm {WB}_{\Lambda })$
. For this, we set
![]() $r \,:\!=\, \sqrt {Tr_\Lambda (\mathsf {G}(\Omega ))} \ge 0$
for a measure
$r \,:\!=\, \sqrt {Tr_\Lambda (\mathsf {G}(\Omega ))} \ge 0$
for a measure
![]() $\mathsf {G} \in \mathcal {M}(\Omega, \mathbb {S}_+^n)$
and identify
$\mathsf {G} \in \mathcal {M}(\Omega, \mathbb {S}_+^n)$
and identify
![]() $\mathsf {G}$
with
$\mathsf {G}$
with
![]() $[\mathsf {G}/r^2,r] \in \mathfrak {C}(\mathcal {M}_1)$
.
$[\mathsf {G}/r^2,r] \in \mathfrak {C}(\mathcal {M}_1)$
.
Theorem 6.3.
Suppose that there holds
![]() $\mathsf {D}^*(\Lambda _2^{-2}) = 0$
and let
$\mathsf {D}^*(\Lambda _2^{-2}) = 0$
and let
![]() $c \,:\!=\, \sqrt {2}n/Tr(\Lambda _2)$
. Then,
$c \,:\!=\, \sqrt {2}n/Tr(\Lambda _2)$
. Then,
![]() $(\mathcal {M}(\Omega, \mathbb {S}_+^n),\mathrm {WB}_\Lambda /c)$
is a metric cone over
$(\mathcal {M}(\Omega, \mathbb {S}_+^n),\mathrm {WB}_\Lambda /c)$
is a metric cone over
![]() $(\mathcal {M}_1, \mathrm {SWB}_\Lambda /c)$
, namely, for
$(\mathcal {M}_1, \mathrm {SWB}_\Lambda /c)$
, namely, for
![]() $\mathsf {G}_0, \mathsf {G}_1 \in \mathcal {M}_1$
and
$\mathsf {G}_0, \mathsf {G}_1 \in \mathcal {M}_1$
and
![]() $r_0,r_1 \ge 0$
,
$r_0,r_1 \ge 0$
,
and
![]() $(\mathcal {M}_1, \mathrm {SWB}_\Lambda /c)$
is a complete geodesic space with
$(\mathcal {M}_1, \mathrm {SWB}_\Lambda /c)$
is a complete geodesic space with
![]() $\mathrm {diam}(\mathcal {M}_1) \le \pi$
.
$\mathrm {diam}(\mathcal {M}_1) \le \pi$
.
Proof. We first prove that
![]() $(\mathcal {M}(\Omega, \mathbb {S}_+^n),\mathrm {WB}_\Lambda /c)$
is a metric cone over
$(\mathcal {M}(\Omega, \mathbb {S}_+^n),\mathrm {WB}_\Lambda /c)$
is a metric cone over
![]() $(\mathcal {M}_1, d)$
for some metric
$(\mathcal {M}_1, d)$
for some metric
![]() $d$
. For this, we note from (3.18) in the proof of Lemma3.9 that
$d$
. For this, we note from (3.18) in the proof of Lemma3.9 that
which yields
![]() $\mathrm {WB}_{\Lambda }^2(\mathsf {G}_0,\mathsf {G}_1) \le 4 c^2$
for
$\mathrm {WB}_{\Lambda }^2(\mathsf {G}_0,\mathsf {G}_1) \le 4 c^2$
for
![]() $\mathsf {G}_0,\mathsf {G}_1 \in \mathcal {M}_1$
. By Lemma6.2, it suffices to check the scaling property (6.4):
$\mathsf {G}_0,\mathsf {G}_1 \in \mathcal {M}_1$
. By Lemma6.2, it suffices to check the scaling property (6.4):
for
![]() $\mathsf {G}_0, \mathsf {G}_1 \in \mathcal {M}_1$
and
$\mathsf {G}_0, \mathsf {G}_1 \in \mathcal {M}_1$
and
![]() $r_0,r_1 \ge 0$
to show that
$r_0,r_1 \ge 0$
to show that
![]() $(\mathcal {M}(\Omega, \mathbb {S}_+^n),\mathrm {WB}_\Lambda /c)$
is a metric cone. Note that (6.6) for the case of
$(\mathcal {M}(\Omega, \mathbb {S}_+^n),\mathrm {WB}_\Lambda /c)$
is a metric cone. Note that (6.6) for the case of
![]() $r_0 = 0$
or
$r_0 = 0$
or
![]() $r_1 = 0$
follows from Proposition4.4. Thus, we can assume
$r_1 = 0$
follows from Proposition4.4. Thus, we can assume
![]() $r_0, r_1 \gt 0$
. Let
$r_0, r_1 \gt 0$
. Let
![]() $\{\mu _t = (\mathsf {G}_t,\mathsf {q}_t,\mathsf {R}_t)\}_{t \in [0,1]} \in \widetilde {\mathcal {CE}}([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
be an admissible curve. We define scalar functions
$\{\mu _t = (\mathsf {G}_t,\mathsf {q}_t,\mathsf {R}_t)\}_{t \in [0,1]} \in \widetilde {\mathcal {CE}}([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
be an admissible curve. We define scalar functions
![]() $b(t) = r_0 + (r_1 - r_0)t$
and
$b(t) = r_0 + (r_1 - r_0)t$
and
![]() $a(t) \,:\!=\, t r_1 /b(t)$
. It is clear that
$a(t) \,:\!=\, t r_1 /b(t)$
. It is clear that
![]() $a(t)$
is strictly increasing with inverse denoted by
$a(t)$
is strictly increasing with inverse denoted by
![]() $t(a)$
. We then define
$t(a)$
. We then define
![]() $\widetilde {\mathsf {G}}_t = b(t)^2\mathsf {G}_{a(t)}$
with
$\widetilde {\mathsf {G}}_t = b(t)^2\mathsf {G}_{a(t)}$
with
which satisfies the continuity equation with end points
![]() $r_0^2 \mathsf {G}_0$
and
$r_0^2 \mathsf {G}_0$
and
![]() $r_1^2 \mathsf {G}_1$
. We now compute
$r_1^2 \mathsf {G}_1$
. We now compute
 \begin{align} \mathcal {J}_{\Lambda, Q}\big (\widetilde {\mathsf {G}},\widetilde {\mathsf {q}},\widetilde {\mathsf {R}}\big ) = & \int _0^1 a^{\prime}(t(a))\, b(t(a))^2 \mathcal {J}_{\Lambda, \Omega }(\mathsf {G}_a, \mathsf {q}_a, \mathsf {R}_a) \, \mathrm {d} a + c^2 (r_1 - r_0)^2 \int _0^1 Tr_\Lambda \mathsf {G}_{a(t)}(\Omega )\, \mathrm {d} t \\ & + c^2 \int _0^1 b(t(a))\, (r_1 - r_0) Tr_\Lambda \mathsf {R}_{a}(\Omega )\, \mathrm {d} a\,. \notag \end{align}
\begin{align} \mathcal {J}_{\Lambda, Q}\big (\widetilde {\mathsf {G}},\widetilde {\mathsf {q}},\widetilde {\mathsf {R}}\big ) = & \int _0^1 a^{\prime}(t(a))\, b(t(a))^2 \mathcal {J}_{\Lambda, \Omega }(\mathsf {G}_a, \mathsf {q}_a, \mathsf {R}_a) \, \mathrm {d} a + c^2 (r_1 - r_0)^2 \int _0^1 Tr_\Lambda \mathsf {G}_{a(t)}(\Omega )\, \mathrm {d} t \\ & + c^2 \int _0^1 b(t(a))\, (r_1 - r_0) Tr_\Lambda \mathsf {R}_{a}(\Omega )\, \mathrm {d} a\,. \notag \end{align}
The last two terms in (6.7) can be simplified by (3.13) on
![]() $[0,1]$
with test function
$[0,1]$
with test function
![]() $\Phi _s = b(t(s)) \,\Lambda _2^{-2}$
:
$\Phi _s = b(t(s)) \,\Lambda _2^{-2}$
:
which implies, thanks to
![]() $Tr_\Lambda \mathsf {G}_0(\Omega ) = Tr_\Lambda \mathsf {G}_1(\Omega ) = 1$
,
$Tr_\Lambda \mathsf {G}_0(\Omega ) = Tr_\Lambda \mathsf {G}_1(\Omega ) = 1$
,
Therefore, by noting
![]() $a^{\prime}(t) b(t)^2 = r_0 r_1$
and using (6.8), it follows that
$a^{\prime}(t) b(t)^2 = r_0 r_1$
and using (6.8), it follows that
which readily gives
![]() $\mathrm {WB}_{\Lambda }^2(r_0^2 \mathsf {G}_0, r_1^2 \mathsf {G}_1)/c^2 \le r_0 r_1 \mathrm {WB}_{\Lambda }^2(\mathsf {G}_0, \mathsf {G}_1)/c^2 + (r_0 - r_1)^2$
. The other direction can be proved similarly. We have proved the existence of
$\mathrm {WB}_{\Lambda }^2(r_0^2 \mathsf {G}_0, r_1^2 \mathsf {G}_1)/c^2 \le r_0 r_1 \mathrm {WB}_{\Lambda }^2(\mathsf {G}_0, \mathsf {G}_1)/c^2 + (r_0 - r_1)^2$
. The other direction can be proved similarly. We have proved the existence of
![]() $(\mathcal {M}_1, d)$
such that
$(\mathcal {M}_1, d)$
such that
![]() $(\mathcal {M}(\Omega, \mathbb {S}_+^n),\mathrm {WB}_\Lambda /c)$
is the associated metric cone.
$(\mathcal {M}(\Omega, \mathbb {S}_+^n),\mathrm {WB}_\Lambda /c)$
is the associated metric cone.
We now show that the metric
![]() $d$
on
$d$
on
![]() $\mathcal {M}_1$
is given by
$\mathcal {M}_1$
is given by
![]() $\mathrm {SWB}_\Lambda /c$
.
$\mathrm {SWB}_\Lambda /c$
.
By Corollary5.7 and [Reference Bridson and Haefliger18, Corollary 5.11], we have that
![]() $(\mathcal {M}_1,d)$
is a geodesic space, which, by Lemma6.1, gives, for
$(\mathcal {M}_1,d)$
is a geodesic space, which, by Lemma6.1, gives, for
![]() $\mathsf {G}_0,\mathsf {G}_1 \in \mathcal {M}_1$
,
$\mathsf {G}_0,\mathsf {G}_1 \in \mathcal {M}_1$
,
It then follows from Theorem5.5 and definition (6.1) that
![]() $d(\mathsf {G}_0,\mathsf {G}_1) = \mathrm {SWB}_{\Lambda }(\mathsf {G}_0,\mathsf {G}_1)/c$
and hence (6.5) holds. Recalling
$d(\mathsf {G}_0,\mathsf {G}_1) = \mathrm {SWB}_{\Lambda }(\mathsf {G}_0,\mathsf {G}_1)/c$
and hence (6.5) holds. Recalling
![]() $\mathrm {WB}_{\Lambda }^2(\mathsf {G}_0,\mathsf {G}_1)/c^2 \le 4$
for
$\mathrm {WB}_{\Lambda }^2(\mathsf {G}_0,\mathsf {G}_1)/c^2 \le 4$
for
![]() $\mathsf {G}_0,\mathsf {G}_1 \in \mathcal {M}_1$
, (6.5) gives
$\mathsf {G}_0,\mathsf {G}_1 \in \mathcal {M}_1$
, (6.5) gives
![]() $0 \le \mathrm {SWB}_\Lambda (\mathsf {G}_0, \mathsf {G}_1)/c \le \pi$
. Finally, for the completeness of
$0 \le \mathrm {SWB}_\Lambda (\mathsf {G}_0, \mathsf {G}_1)/c \le \pi$
. Finally, for the completeness of
![]() $(\mathcal {M}_1, \mathrm {SWB}_\Lambda /c)$
, it suffices to note that
$(\mathcal {M}_1, \mathrm {SWB}_\Lambda /c)$
, it suffices to note that
![]() $\mathrm {SWB}_\Lambda$
and
$\mathrm {SWB}_\Lambda$
and
![]() $\mathrm {WB}_\Lambda$
are topologically equivalent on
$\mathrm {WB}_\Lambda$
are topologically equivalent on
![]() $\mathcal {M}_1$
, again by (6.5), and
$\mathcal {M}_1$
, again by (6.5), and
![]() $\mathcal {M}_1$
is a closed set in
$\mathcal {M}_1$
is a closed set in
![]() $(\mathcal {M}(\Omega, \mathbb {S}_+^n),\mathrm {WB}_\Lambda )$
by Proposition5.2.
$(\mathcal {M}(\Omega, \mathbb {S}_+^n),\mathrm {WB}_\Lambda )$
by Proposition5.2.
7. Example and discussion
In this section, we detail the connections between our model (
![]() $\mathcal {P}$
) and the existing ones.
$\mathcal {P}$
) and the existing ones.
Example 7.1.
(Kantorovich–Bures metric [16]). We set the dimension parameters
![]() $n = m =d$
and
$n = m =d$
and
![]() $k = 1$
and the weight matrices
$k = 1$
and the weight matrices
![]() $\Lambda _i = I$
for
$\Lambda _i = I$
for
![]() $i = 1, 2$
in (3.1) and consider the differential operator
$i = 1, 2$
in (3.1) and consider the differential operator
![]() $\mathsf {D} = \nabla _s$
for the continuity equation (3.13), where
$\mathsf {D} = \nabla _s$
for the continuity equation (3.13), where
![]() $ \nabla _s$
is the symmetric gradient defined by
$ \nabla _s$
is the symmetric gradient defined by
![]() $\nabla _s(q) = \frac {1}{2}(\nabla q + (\nabla q)^{\mathrm {T}})$
for a smooth vector field
$\nabla _s(q) = \frac {1}{2}(\nabla q + (\nabla q)^{\mathrm {T}})$
for a smooth vector field
![]() $q \in C_c^\infty (\mathbb {R}^d,\mathbb {R}^d)$
. Then, (
$q \in C_c^\infty (\mathbb {R}^d,\mathbb {R}^d)$
. Then, (
![]() $\mathcal {P}$
) gives the convex formulation of the Kantorovich–Bures metric
$\mathcal {P}$
) gives the convex formulation of the Kantorovich–Bures metric
![]() $d_{KB}$
on
$d_{KB}$
on
![]() $\mathcal {M}(\Omega, \mathbb {S}_+^d)$
[16, Definition 2.1]:
$\mathcal {M}(\Omega, \mathbb {S}_+^d)$
[16, Definition 2.1]:
 \begin{align} \mathrm {WB}^2_{(I,I)}(\mathsf {G}_0,\mathsf {G}_1)&= \frac {1}{2}d^2_{KB}(\mathsf {G}_0,\mathsf {G}_1) = \inf \big \{\mathcal {J}_{\Lambda, Q}(\mu ) \,;\ \mu = \mathsf {(G,q,R)} \in \mathcal {M}(Q,\mathbb {X})\ \text {satisfies} \notag \\ \partial _t \mathsf {G} &= \{ - \nabla \mathsf {q}_t + \mathsf {R}_t\}^{\mathrm {sym}} \ \text {with}\ \mathsf {G}_t|_{t = 0} = \mathsf {G}_0\,,\ \mathsf {G}_t|_{t = 1} = \mathsf {G}_1 \big \}\,, \end{align}
\begin{align} \mathrm {WB}^2_{(I,I)}(\mathsf {G}_0,\mathsf {G}_1)&= \frac {1}{2}d^2_{KB}(\mathsf {G}_0,\mathsf {G}_1) = \inf \big \{\mathcal {J}_{\Lambda, Q}(\mu ) \,;\ \mu = \mathsf {(G,q,R)} \in \mathcal {M}(Q,\mathbb {X})\ \text {satisfies} \notag \\ \partial _t \mathsf {G} &= \{ - \nabla \mathsf {q}_t + \mathsf {R}_t\}^{\mathrm {sym}} \ \text {with}\ \mathsf {G}_t|_{t = 0} = \mathsf {G}_0\,,\ \mathsf {G}_t|_{t = 1} = \mathsf {G}_1 \big \}\,, \end{align}
for
![]() $\mathsf {G}_0, \mathsf {G}_1 \in \mathcal {M}(\Omega, \mathbb {S}^d_+)$
, where
$\mathsf {G}_0, \mathsf {G}_1 \in \mathcal {M}(\Omega, \mathbb {S}^d_+)$
, where
![]() $\mathcal {J}_{\Lambda, Q}(\mu )$
with
$\mathcal {J}_{\Lambda, Q}(\mu )$
with
![]() $\Lambda = (I,I)$
is given by (3.24):
$\Lambda = (I,I)$
is given by (3.24):
Example 7.2.
(Wasserstein–Fisher–Rao metric [27, 56, 64]). If we set
![]() $n = m = 1$
,
$n = m = 1$
,
![]() $k = d$
and
$k = d$
and
![]() $\Lambda _1 = \sqrt {\alpha } I$
,
$\Lambda _1 = \sqrt {\alpha } I$
,
![]() $\Lambda _2 = \sqrt {\beta }I$
with
$\Lambda _2 = \sqrt {\beta }I$
with
![]() $\alpha, \beta \gt 0$
, and consider the differential operator
$\alpha, \beta \gt 0$
, and consider the differential operator
![]() $\mathsf {D} = \mathrm {div}$
, then (
$\mathsf {D} = \mathrm {div}$
, then (
![]() $\mathcal {P}$
) gives the Wasserstein–Fisher–Rao metric [64, (3.1)]: for given distributions
$\mathcal {P}$
) gives the Wasserstein–Fisher–Rao metric [64, (3.1)]: for given distributions
![]() $\rho _0, \rho _1 \in \mathcal {M}(\Omega, \mathbb {R}_+)$
,
$\rho _0, \rho _1 \in \mathcal {M}(\Omega, \mathbb {R}_+)$
,
Example 7.3.
(Matricial interpolation distance [25]). Let
![]() $N$
be a positive integer and
$N$
be a positive integer and
![]() $(\mathbb {M}^n)^N$
denote the space of block-row vectors
$(\mathbb {M}^n)^N$
denote the space of block-row vectors
![]() $(A_1,\ldots, A_N)$
with
$(A_1,\ldots, A_N)$
with
![]() $A_i \in \mathbb {M}^n$
. The spaces
$A_i \in \mathbb {M}^n$
. The spaces
![]() $(\mathbb {S}^n)^N$
and
$(\mathbb {S}^n)^N$
and
![]() $(\mathbb {A}^n)^N$
are defined similarly. For
$(\mathbb {A}^n)^N$
are defined similarly. For
![]() $M \in (\mathbb {M}^n)^N$
, we define its component transpose by
$M \in (\mathbb {M}^n)^N$
, we define its component transpose by
![]() $M^t \,:\!=\, (M_1^{\mathrm {T}},\ldots, M_N^{\mathrm {T}})$
. We fix a sequence of symmetric matrices
$M^t \,:\!=\, (M_1^{\mathrm {T}},\ldots, M_N^{\mathrm {T}})$
. We fix a sequence of symmetric matrices
![]() $\{L_k\}_{k=1}^N \subset \mathbb {S}^n$
and define the linear operator
$\{L_k\}_{k=1}^N \subset \mathbb {S}^n$
and define the linear operator
![]() $\nabla _L : \mathbb {S}^n \to (\mathbb {A}^n)^N$
by
$\nabla _L : \mathbb {S}^n \to (\mathbb {A}^n)^N$
by
![]() $(\nabla _L X)_k = L_k X - XL_k$
. We denote by
$(\nabla _L X)_k = L_k X - XL_k$
. We denote by
![]() $\nabla _L^*$
its dual operator with respect to the Frobenius inner product. We now let
$\nabla _L^*$
its dual operator with respect to the Frobenius inner product. We now let
![]() $k = n (d + N)$
and write
$k = n (d + N)$
and write
![]() $\mathsf {q} \in \mathcal {M}(Q, \mathbb {R}^{n \times k})$
for
$\mathsf {q} \in \mathcal {M}(Q, \mathbb {R}^{n \times k})$
for
![]() $[\mathsf {q}_0, \mathsf {q}_1]$
with
$[\mathsf {q}_0, \mathsf {q}_1]$
with
![]() $\mathsf {q}_0 \in \mathcal {M}(Q, (\mathbb {M}^n)^d)$
and
$\mathsf {q}_0 \in \mathcal {M}(Q, (\mathbb {M}^n)^d)$
and
![]() $\mathsf {q}_1 \in \mathcal {M}(Q,(\mathbb {M}^n)^N)$
. With the above notions, we define
$\mathsf {q}_1 \in \mathcal {M}(Q,(\mathbb {M}^n)^N)$
. With the above notions, we define
Then, it is clear that (
![]() $\mathcal {P}$
) with weight matrices
$\mathcal {P}$
) with weight matrices
![]() $\Lambda _i = I$
for
$\Lambda _i = I$
for
![]() $i = 1,2$
gives the model in [25, (5.7a)–(5.7c)]:
$i = 1,2$
gives the model in [25, (5.7a)–(5.7c)]:
 \begin{align} \mathrm {W}_{2,\mathrm {FR}}(\mathsf {G}_0, \mathsf {G}_1)^2 &= \frac {1}{2} \inf \big \{ \lVert G^\dagger q_0 \rVert ^2_{L^2_{\mathsf {G}(Q)}} + \lVert G^\dagger q_1 \rVert ^2_{L^2_{\mathsf {G}(Q)}} + \lVert G^\dagger R \rVert ^2_{L^2_{\mathsf {G}(Q)}}\,; \nonumber \\ \partial _t \mathsf {G} &= - \frac {1}{2}\mathrm {div} (\mathsf {q}_0 + \mathsf {q}_0^t) + \frac {1}{2}\nabla _L^* (\mathsf {q}_1 - \mathsf {q}_1^t) + \mathsf {R}^{\mathrm {sym}}\ \text {with}\ \mathsf {G}_t|_{t = 0} = \mathsf {G}_0\,,\ \mathsf {G}_t|_{t = 1} = \mathsf {G}_1 \big \}\,. \end{align}
\begin{align} \mathrm {W}_{2,\mathrm {FR}}(\mathsf {G}_0, \mathsf {G}_1)^2 &= \frac {1}{2} \inf \big \{ \lVert G^\dagger q_0 \rVert ^2_{L^2_{\mathsf {G}(Q)}} + \lVert G^\dagger q_1 \rVert ^2_{L^2_{\mathsf {G}(Q)}} + \lVert G^\dagger R \rVert ^2_{L^2_{\mathsf {G}(Q)}}\,; \nonumber \\ \partial _t \mathsf {G} &= - \frac {1}{2}\mathrm {div} (\mathsf {q}_0 + \mathsf {q}_0^t) + \frac {1}{2}\nabla _L^* (\mathsf {q}_1 - \mathsf {q}_1^t) + \mathsf {R}^{\mathrm {sym}}\ \text {with}\ \mathsf {G}_t|_{t = 0} = \mathsf {G}_0\,,\ \mathsf {G}_t|_{t = 1} = \mathsf {G}_1 \big \}\,. \end{align}
We next relate our model (
![]() $\mathcal {P}$
) to the matrix-valued optimal ballistic transport problems in refs. [Reference Brenier15, Reference Vorotnikov91]. As reviewed in the introduction, Brenier [Reference Brenier15] recently attempted to find the weak solution of the incompressible Euler equation on the domain
$\mathcal {P}$
) to the matrix-valued optimal ballistic transport problems in refs. [Reference Brenier15, Reference Vorotnikov91]. As reviewed in the introduction, Brenier [Reference Brenier15] recently attempted to find the weak solution of the incompressible Euler equation on the domain
![]() $[0,T] \times \Omega \subset \mathbb {R}^{1 + d}$
(we omit the initial and boundary conditions for simplicity):
$[0,T] \times \Omega \subset \mathbb {R}^{1 + d}$
(we omit the initial and boundary conditions for simplicity):
by minimising the kinetic energy
![]() $\int _0^T\int _\Omega |v(t,x)|^2 \, \mathrm {d} x\, \mathrm {d} t$
, where
$\int _0^T\int _\Omega |v(t,x)|^2 \, \mathrm {d} x\, \mathrm {d} t$
, where
![]() $v$
is a
$v$
is a
![]() $\mathbb {R}^n$
-valued vector field and
$\mathbb {R}^n$
-valued vector field and
![]() $p$
is a scalar function. It turns out that this problem admits a concave maximisation dual problem, to which the relaxed solution always exists under very light assumptions. Such an approach was extended by Vorotnikov [Reference Vorotnikov91] in an abstract functional analytic framework that includes a broad class of PDEs with quadratic nonlinearity as examples, such as the Hamilton–Jacobi equation, the template matching equation, and the multidimensional Camassa–Holm equation. More precisely, [Reference Vorotnikov91] considered the following abstract Euler equation on
$p$
is a scalar function. It turns out that this problem admits a concave maximisation dual problem, to which the relaxed solution always exists under very light assumptions. Such an approach was extended by Vorotnikov [Reference Vorotnikov91] in an abstract functional analytic framework that includes a broad class of PDEs with quadratic nonlinearity as examples, such as the Hamilton–Jacobi equation, the template matching equation, and the multidimensional Camassa–Holm equation. More precisely, [Reference Vorotnikov91] considered the following abstract Euler equation on
![]() $[0,T] \times \Omega$
:
$[0,T] \times \Omega$
:
where
![]() $\mathsf {P}$
is an orthogonal projection and
$\mathsf {P}$
is an orthogonal projection and
![]() $\mathsf {L}: L^2(\Omega, \mathbb {S}^n) \to L^2(\Omega, \mathbb {R}^n)$
is a (closed densely defined) linear operator. One can see that for
$\mathsf {L}: L^2(\Omega, \mathbb {S}^n) \to L^2(\Omega, \mathbb {R}^n)$
is a (closed densely defined) linear operator. One can see that for
![]() $\mathsf {L} = - \mathrm {div}$
and
$\mathsf {L} = - \mathrm {div}$
and
![]() $\mathsf {P}$
being the Leray projection, the problem (7.2) reduces to (7.1). The dual problem associated with the weak solution of (7.2) with minimal kinetic energy reads as follows:
$\mathsf {P}$
being the Leray projection, the problem (7.2) reduces to (7.1). The dual problem associated with the weak solution of (7.2) with minimal kinetic energy reads as follows:
where
![]() $G$
and
$G$
and
![]() $q$
are
$q$
are
![]() $\mathbb {S}^n_{+}$
-valued and
$\mathbb {S}^n_{+}$
-valued and
![]() $\mathbb {R}^n$
-valued vector fields, respectively. Note that the Hamilton–Jacobi equation
$\mathbb {R}^n$
-valued vector fields, respectively. Note that the Hamilton–Jacobi equation
![]() $\partial _t \psi + \frac {1}{2} |\nabla \psi |^2 = 0$
can be reformulated as
$\partial _t \psi + \frac {1}{2} |\nabla \psi |^2 = 0$
can be reformulated as
![]() $\partial _t v + \frac {1}{2} \nabla Tr(v \otimes v) = 0$
by letting
$\partial _t v + \frac {1}{2} \nabla Tr(v \otimes v) = 0$
by letting
![]() $v = \nabla \psi$
, which is a special case of (7.2) with
$v = \nabla \psi$
, which is a special case of (7.2) with
![]() $\mathsf {P} = I$
and
$\mathsf {P} = I$
and
![]() $\mathsf {L} = - \frac {1}{2} \nabla Tr$
. The corresponding dual maximisation problem is given by
$\mathsf {L} = - \frac {1}{2} \nabla Tr$
. The corresponding dual maximisation problem is given by
which closely relates to the ballistic transport problem [Reference Barton and Ghoussoub5]. In view of (7.3) and (7.4), one may regard
as a matricial continuity equation, and our model (3.14) can be hence viewed as an unbalanced variant of (7.5). Then, the conservativity condition
![]() $\mathsf {D}^*(I) = 0$
for (7.5) is simply
$\mathsf {D}^*(I) = 0$
for (7.5) is simply
![]() $\mathsf {P} \circ \mathsf {L}(I) = 0$
, which has been used to guarantee the existence of a measure-valued solution to (7.3); see [Reference Vorotnikov91, Theorem 4.6]. Thanks to the above observations, one may expect that each meaningful choice of
$\mathsf {P} \circ \mathsf {L}(I) = 0$
, which has been used to guarantee the existence of a measure-valued solution to (7.3); see [Reference Vorotnikov91, Theorem 4.6]. Thanks to the above observations, one may expect that each meaningful choice of
![]() $\mathsf {L}$
and
$\mathsf {L}$
and
![]() $\mathsf {P}$
in [Reference Vorotnikov91, Section 6] can generate a reasonable distance (
$\mathsf {P}$
in [Reference Vorotnikov91, Section 6] can generate a reasonable distance (
![]() $\mathcal {P}$
) with
$\mathcal {P}$
) with
![]() $\mathsf {D} = 2 (\mathsf {L}^* \circ \mathsf {P})$
. For instance, setting
$\mathsf {D} = 2 (\mathsf {L}^* \circ \mathsf {P})$
. For instance, setting
![]() $n = d$
,
$n = d$
,
![]() $\mathsf {P} = I$
and
$\mathsf {P} = I$
and
![]() $\mathsf {L} = - \mathrm {div} - \frac {1}{2} \nabla Tr$
in (7.2) gives the template matching equation
$\mathsf {L} = - \mathrm {div} - \frac {1}{2} \nabla Tr$
in (7.2) gives the template matching equation
![]() $\partial _t v + \mathrm {div}\, (v \otimes v) + \frac {1}{2} \nabla |v|^2 = 0$
and a distance (
$\partial _t v + \mathrm {div}\, (v \otimes v) + \frac {1}{2} \nabla |v|^2 = 0$
and a distance (
![]() $\mathcal {P}$
) with
$\mathcal {P}$
) with
![]() $\mathsf {D} = 2 (\mathsf {L}^* \circ \mathsf {P})$
:
$\mathsf {D} = 2 (\mathsf {L}^* \circ \mathsf {P})$
:
Remark 7.1.
An important question is how to compare these matrix-valued OT models (
![]() $\mathcal {P}_{\mathrm {WB}}$
), (
$\mathcal {P}_{\mathrm {WB}}$
), (
![]() $\mathcal {P}_{2,\mathrm {FR}}$
), and
(7.6)
(as well as others in the literature), which requires a deeper theoretical analysis and is completely open, to the best of our knowledge.
$\mathcal {P}_{2,\mathrm {FR}}$
), and
(7.6)
(as well as others in the literature), which requires a deeper theoretical analysis and is completely open, to the best of our knowledge.
8. Concluding remarks
We have proposed a general class of unbalanced matrix-valued OT distances
![]() $\mathrm {WB}_{\Lambda }(\cdot, \cdot )$
over the space
$\mathrm {WB}_{\Lambda }(\cdot, \cdot )$
over the space
![]() $\mathcal {M}(\Omega, \mathbb {S}^n_+)$
, called the weighted Wasserstein–Bures metric. The definition relies on a dynamic formulation and convex analysis. We have shown that
$\mathcal {M}(\Omega, \mathbb {S}^n_+)$
, called the weighted Wasserstein–Bures metric. The definition relies on a dynamic formulation and convex analysis. We have shown that
![]() $\mathcal {M}(\Omega, \mathbb {S}^n_+)$
equipped with the metric
$\mathcal {M}(\Omega, \mathbb {S}^n_+)$
equipped with the metric
![]() $\mathrm {WB}_{\Lambda }(\cdot, \cdot )$
is a complete geodesic space, and it can be viewed as a metric cone. In the follow-up work [Reference Li and Zou63], we have considered the convergence of the discrete approximation of the transport model (
$\mathrm {WB}_{\Lambda }(\cdot, \cdot )$
is a complete geodesic space, and it can be viewed as a metric cone. In the follow-up work [Reference Li and Zou63], we have considered the convergence of the discrete approximation of the transport model (
![]() $\mathcal {P}$
). Our results provide a unified framework for unbalanced transport distances on matrix-valued measures and directly apply to various existing models such as the Kantorovich–Bures distance (
$\mathcal {P}$
). Our results provide a unified framework for unbalanced transport distances on matrix-valued measures and directly apply to various existing models such as the Kantorovich–Bures distance (
![]() $\mathcal {P}_{\mathrm {WB}}$
), the matricial interpolation distance (
$\mathcal {P}_{\mathrm {WB}}$
), the matricial interpolation distance (
![]() $\mathcal {P}_{2,\mathrm {FR}}$
) and the WFR one (
$\mathcal {P}_{2,\mathrm {FR}}$
) and the WFR one (
![]() $\mathcal {P}_{\mathrm {WFR}}$
). Meanwhile, it paves the way for practical applications, in particular, diffusion tensor imaging as in refs. [Reference Chen, Haber, Yamamoto, Georgiou and Tannenbaum26, Reference Peyré, Chizat, Vialard and Solomon77, Reference Ryu, Chen, Li and Osher86].
$\mathcal {P}_{\mathrm {WFR}}$
). Meanwhile, it paves the way for practical applications, in particular, diffusion tensor imaging as in refs. [Reference Chen, Haber, Yamamoto, Georgiou and Tannenbaum26, Reference Peyré, Chizat, Vialard and Solomon77, Reference Ryu, Chen, Li and Osher86].
Acknowledgements
The authors would like to thank the anonymous referees and editors for their careful reading and constructive comments and suggestions, which have helped us improve this work.
Financial Support
The work of Bowen Li is supported in part by National Key R&D Program of China (project 2024YFA1016000). Jun Zou was substantially supported by Hong Kong RGC General Research Fund (projects 14308322 and 14306921) and NSFC/Hong Kong RGC Joint Research Scheme 2022/23 (project N_CUHK465/22).
Competing interests
The authors declare none.
Appendix A: Auxiliary proofs
Proof of Lemma
4.1. For
![]() $\mu \in \mathcal {M}(\mathcal {X},\mathbb {X})$
, by definition, we have
$\mu \in \mathcal {M}(\mathcal {X},\mathbb {X})$
, by definition, we have
![]() $ \iota _{C(\mathcal {X},\mathcal {O}_\Lambda )}^*(\mu ) = \sup \{\langle \mu, \Xi \rangle _{\mathcal {X}}\,;\, \Xi \in C(\mathcal {X},\mathcal {O}_\Lambda ) \}\,.$
To show that the admissible set
$ \iota _{C(\mathcal {X},\mathcal {O}_\Lambda )}^*(\mu ) = \sup \{\langle \mu, \Xi \rangle _{\mathcal {X}}\,;\, \Xi \in C(\mathcal {X},\mathcal {O}_\Lambda ) \}\,.$
To show that the admissible set
![]() $C(\mathcal {X},\mathcal {O}_\Lambda )$
can be relaxed to
$C(\mathcal {X},\mathcal {O}_\Lambda )$
can be relaxed to
![]() $L^\infty _{|\mu |} (\mathcal {X},\mathcal {O}_\Lambda )$
, it suffices to prove
$L^\infty _{|\mu |} (\mathcal {X},\mathcal {O}_\Lambda )$
, it suffices to prove
For this, we consider an essentially bounded measurable field
![]() $\Xi \in L_{|\mu |}^\infty (\mathcal {X},\mathcal {O}_\Lambda )$
. Without loss of generality, we assume that it is bounded by
$\Xi \in L_{|\mu |}^\infty (\mathcal {X},\mathcal {O}_\Lambda )$
. Without loss of generality, we assume that it is bounded by
![]() $\lVert \Xi \rVert _\infty$
everywhere. By Lusin’s theorem, for any
$\lVert \Xi \rVert _\infty$
everywhere. By Lusin’s theorem, for any
![]() $\varepsilon \gt 0$
, there exists a continuous field with compact support
$\varepsilon \gt 0$
, there exists a continuous field with compact support
![]() $\widetilde {\Xi }$
such that
$\widetilde {\Xi }$
such that
Define
![]() $\mathbb {P}_{\mathcal {O}_\Lambda }$
as the
$\mathbb {P}_{\mathcal {O}_\Lambda }$
as the
![]() $L^2$
-projection from
$L^2$
-projection from
![]() $\mathbb {X}$
to the closed convex set
$\mathbb {X}$
to the closed convex set
![]() $\mathcal {O}_\Lambda$
. By abuse of notation, we still denote by
$\mathcal {O}_\Lambda$
. By abuse of notation, we still denote by
![]() $\widetilde {\Xi }$
the composite function
$\widetilde {\Xi }$
the composite function
![]() $\mathbb {P}_{\mathcal {O}_\Lambda } \circ \widetilde {\Xi } \in C(\mathcal {X},\mathcal {O}_\Lambda )$
. It is clear that
$\mathbb {P}_{\mathcal {O}_\Lambda } \circ \widetilde {\Xi } \in C(\mathcal {X},\mathcal {O}_\Lambda )$
. It is clear that
![]() $\lVert \widetilde {\Xi } \rVert _\infty \le \lVert \Xi \rVert _\infty$
, and (A.2) still holds. Then it follows that
$\lVert \widetilde {\Xi } \rVert _\infty \le \lVert \Xi \rVert _\infty$
, and (A.2) still holds. Then it follows that
![]() $ | \langle \mu, \Xi \rangle _{\mathcal {X}} - \langle \mu, \widetilde {\Xi } \rangle _{\mathcal {X}}| \le 2 \varepsilon \lVert \Xi \rVert _\infty \,,$
which further implies
$ | \langle \mu, \Xi \rangle _{\mathcal {X}} - \langle \mu, \widetilde {\Xi } \rangle _{\mathcal {X}}| \le 2 \varepsilon \lVert \Xi \rVert _\infty \,,$
which further implies
Since
![]() $\varepsilon$
is arbitrary, we have proved the claim (A.1). Thus, we can take the pointwise
$\varepsilon$
is arbitrary, we have proved the claim (A.1). Thus, we can take the pointwise
![]() $\sup$
in (4.4) and obtain the desired
$\sup$
in (4.4) and obtain the desired
![]() $\iota _{C(\mathcal {X},\mathcal {O}_\Lambda )}^*(\mu ) = \mathcal {J}_{\Lambda, \mathcal {X}}(\mu )$
by Proposition3.1. Next, we characterise the subgradient
$\iota _{C(\mathcal {X},\mathcal {O}_\Lambda )}^*(\mu ) = \mathcal {J}_{\Lambda, \mathcal {X}}(\mu )$
by Proposition3.1. Next, we characterise the subgradient
![]() $\partial \mathcal {J}_{\Lambda, \mathcal {X}}(\mu )$
. By Lemma2.4, we have
$\partial \mathcal {J}_{\Lambda, \mathcal {X}}(\mu )$
. By Lemma2.4, we have
![]() $\Xi \in \partial \mathcal {J}_{\Lambda, \mathcal {X}}(\mu ) \bigcap C(\mathcal {X},\mathbb {X})$
if and only if
$\Xi \in \partial \mathcal {J}_{\Lambda, \mathcal {X}}(\mu ) \bigcap C(\mathcal {X},\mathbb {X})$
if and only if
![]() $ \langle \mu, \Xi \rangle _{\mathcal {X}} = \iota _{C(\mathcal {X},\mathcal {O}_\Lambda )}(\Xi ) + \mathcal {J}_{\Lambda, \mathcal {X}}(\mu ) \,,$
which yields
$ \langle \mu, \Xi \rangle _{\mathcal {X}} = \iota _{C(\mathcal {X},\mathcal {O}_\Lambda )}(\Xi ) + \mathcal {J}_{\Lambda, \mathcal {X}}(\mu ) \,,$
which yields
![]() $\Xi \in C(\mathcal {X},\mathcal {O}_\Lambda )$
and
$\Xi \in C(\mathcal {X},\mathcal {O}_\Lambda )$
and
where
![]() $\lambda$
is a reference measure such that
$\lambda$
is a reference measure such that
![]() $|\mu | \ll \lambda$
and
$|\mu | \ll \lambda$
and
![]() $\mu _\lambda$
is the density of
$\mu _\lambda$
is the density of
![]() $\mu$
. We note from
$\mu$
. We note from
![]() $J_\Lambda = \iota ^*_{\mathcal {O}_\Lambda }$
and
$J_\Lambda = \iota ^*_{\mathcal {O}_\Lambda }$
and
![]() $\Xi (x) \in \mathcal {O}_\Lambda$
that
$\Xi (x) \in \mathcal {O}_\Lambda$
that
![]() $ \mu _\lambda \cdot \Xi - J_\Lambda (\mu _\lambda ) \le 0$
,
$ \mu _\lambda \cdot \Xi - J_\Lambda (\mu _\lambda ) \le 0$
,
![]() $\lambda$
-a.e., where by (A.3), the equality actually holds
$\lambda$
-a.e., where by (A.3), the equality actually holds
![]() $\lambda$
-a.e.. Then (4.5) follows.
$\lambda$
-a.e.. Then (4.5) follows.
Proof of Lemma
5.1. It suffices to consider
![]() $[a,b] = [0,1]$
. We denote by
$[a,b] = [0,1]$
. We denote by
![]() $\widetilde {\mathrm {WB}}_\Lambda$
the right-hand side of (5.1). By Hölder’s inequality and recalling (
$\widetilde {\mathrm {WB}}_\Lambda$
the right-hand side of (5.1). By Hölder’s inequality and recalling (
![]() $\mathcal {P}$
) with the admissible set
$\mathcal {P}$
) with the admissible set
![]() $\widetilde {\mathcal {CE}}([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
, we have
$\widetilde {\mathcal {CE}}([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
, we have
![]() $\widetilde {\mathrm {WB}}_\Lambda \le \mathrm {WB}_\Lambda$
. For the other direction, we consider
$\widetilde {\mathrm {WB}}_\Lambda \le \mathrm {WB}_\Lambda$
. For the other direction, we consider
![]() $\{\mu _t\}_{t \in [0,1]} \in \widetilde {\mathcal {CE}}([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
and reparameterize it by the
$\{\mu _t\}_{t \in [0,1]} \in \widetilde {\mathcal {CE}}([0,1];\,\mathsf {G}_0,\mathsf {G}_1)$
and reparameterize it by the
![]() $\varepsilon$
-arc length function
$\varepsilon$
-arc length function
![]() $s = \mathsf {s}_\varepsilon (t)$
:
$s = \mathsf {s}_\varepsilon (t)$
:
where
![]() $L(\mu _t)\,:\!=\, \int _0^1 \mathcal {J}_{\Lambda, \Omega }(\mu _\tau )^{1/2}\, \mathrm {d} \tau$
. It is clear that
$L(\mu _t)\,:\!=\, \int _0^1 \mathcal {J}_{\Lambda, \Omega }(\mu _\tau )^{1/2}\, \mathrm {d} \tau$
. It is clear that
![]() $\mathsf {s}_\varepsilon (t)$
is strictly increasing and absolutely continuous and has an absolutely continuous inverse. Then, by Lemma3.15 and writing
$\mathsf {s}_\varepsilon (t)$
is strictly increasing and absolutely continuous and has an absolutely continuous inverse. Then, by Lemma3.15 and writing
![]() $\widetilde {\mu }^\varepsilon _s = \mu _{\mathsf {s}_\varepsilon ^{-1}(s)}$
for short, we have
$\widetilde {\mu }^\varepsilon _s = \mu _{\mathsf {s}_\varepsilon ^{-1}(s)}$
for short, we have
where the first inequality is by (
![]() $\mathcal {P}^{\prime}$
) with
$\mathcal {P}^{\prime}$
) with
![]() $[a,b] = [0, L(\mu _t) + \varepsilon ]$
. Letting
$[a,b] = [0, L(\mu _t) + \varepsilon ]$
. Letting
![]() $\varepsilon \to 0$
in (A.4), we can find
$\varepsilon \to 0$
in (A.4), we can find
![]() $\mathrm {WB}_{\Lambda } \le \widetilde {\mathrm {WB}}_\Lambda$
. If we assume that
$\mathrm {WB}_{\Lambda } \le \widetilde {\mathrm {WB}}_\Lambda$
. If we assume that
![]() $\mu$
minimises (
$\mu$
minimises (
![]() $\mathcal {P}$
), we have
$\mathcal {P}$
), we have
which implies that
![]() $\mathcal {J}_{\Lambda, \Omega }(\mu _t)$
is constant a.e.. Then (5.2) immediately follows.
$\mathcal {J}_{\Lambda, \Omega }(\mu _t)$
is constant a.e.. Then (5.2) immediately follows.