Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-23T05:01:41.209Z Has data issue: false hasContentIssue false
  • English
  • Français

Rigorous results in existence and selection of Saffman–Taylor fingers by kinetic undercooling

Published online by Cambridge University Press:  10 January 2018

XUMING XIE
XUMING XIE*
Affiliation:
Department of Mathematics, Morgan State University, Baltimore, MD 21251, USA email: xuming.xie@morgan.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

The selection of Saffman–Taylor fingers by surface tension has been extensively investigated. In this paper, we are concerned with the existence and selection of steadily translating symmetric finger solutions in a Hele–Shaw cell by small but non-zero kinetic undercooling (ε2). We rigorously conclude that for relative finger width λ near one half, symmetric finger solutions exist in the asymptotic limit of undercooling ε2 → 0 if the Stokes multiplier for a relatively simple non-linear differential equation is zero. This Stokes multiplier S depends on the parameter 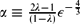$\alpha \equiv \frac{2 \lambda -1}{(1-\lambda)}\epsilon^{-\frac{4}{3}}$ and earlier calculations have shown this to be zero for a discrete set of values of α. While this result is similar to that obtained previously for Saffman–Taylor fingers by surface tension, the analysis for the problem with kinetic undercooling exhibits a number of subtleties as pointed out by Chapman and King (2003, The selection of Saffman–Taylor fingers by kinetic undercooling, Journal of Engineering Mathematics, 46, 1–32). The main subtlety is the behaviour of the Stokes lines at the finger tip, where the analysis is complicated by non-analyticity of coefficients in the governing equation.

Keywords

finger selectionHele–Shawkinetic undercoolingexistenceanalytic solution
Type
Papers
Information
European Journal of Applied Mathematics , Volume 30 , Issue 1 , February 2019 , pp. 63 - 116
Copyright
Copyright © Cambridge University Press 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Anjos, P. H. A., Dias, E. O. & Miranda, J. A. (2015) Kinetic undercooling in Hele–Shaw flows. Phys. Rev. E 92 (2), 043019.Google Scholar
[2] Back, J. M., McCue, S. W., Hsieh, M. N. & Moroney, T. J. (2014) The effect of surface tension and kinetic undercooling on a radially-symmetric melting problem. Appl. Math. Comp. 229, 41–52.Google Scholar
[3] Carrier, G. F., Krook, M. & Pearson, C. E. (1966) Functions of a Complex Variable, McGraw-Hill, New York.Google Scholar
[4] Chapman, S. J. (1999) On the role of Stokes lines in the selection of Saffman–Taylor fingers with small surface tension. Eur. J. Appl Math. 10, 513–534.Google Scholar
[5] Chapman, S. J. & King, J. R. (2003) The selection of Saffman–Taylor fingers by kinetic undercooling. J. Eng. Math. 46, 1–32.Google Scholar
[6] Combescot, R., Hakim, V., Dombre, T., Pomeau, Y. & Pumir, A. (1986) Shape selection for Saffman–Taylor fingers. Phys. Rev. Lett. 56 (19), 2036–2039.Google Scholar
[7] Cohen, D. S. & Erneux, T. (1988) Free boundary problems in controlled release pharmaceuticals I: Diffusion in glassy polymers. SIAM, J. Appl. Math. 48, 1451–1465.Google Scholar
[8] Combescot, R., Hakim, V., Dombre, T., Pomeau, Y. & Pumir, A. (1988) Analytic theory of Saffman–Taylor fingers. Phys. Rev. A 37 (4), 1270–1283.Google Scholar
[9] Combescot, R. & Dombre, T. (1988) Selection in the Saffman–Taylor bubble and asymmetrical finger problem. Phys. Rev. A 38, 2573–2581.Google Scholar
[10] Costin, O. (1995) Exponential asymptotics, transseries, and generalized borel summation for analytic, nonlinear, rank-one systems of ordinary differential equations. IMRN 8, 377–417.Google Scholar
[11] Costin, O. (1998) On borel summation and stokes phenomena for rank-one systems of ordinary differential equations. Duke Math. J. 93 (2), 289–343.Google Scholar
[12] Dallaston, M. C. & McCue, S. W. (2014) Corner and finger formation in Hele–Shaw flow with kinetic undercooling regularization. Eur. J. Appl. Math. 25 (6), 707–727.Google Scholar
[13] Ebert, U., Meulenbroek, B. & Schafer, L. (2007) Convective stabilization of a Laplacian moving boundary problem with kinetic undercooling. SIAM J. Appl. Math. 68 (1), 292–310.Google Scholar
[14] Evans, J. D. & King, J. R. (2000) Asymptotic results for the Stefan problem with kinetic undercooling. Q. J. Mech. Appl. Math. 53, 449–473.Google Scholar
[15] Gardiner, B. P. J., McCue, S. W., Dallaston, M. C. & Moroney, T. J. (2015) Saffman–Taylor fingers with kinetic undercooling. Phys. Rev. E 91 (2), 023016.Google Scholar
[16] Hille, E. (1976) Ordinary Differential Equations in the Complex Domain, Wiley-Interscience, Mineola, New York.Google Scholar
[17] Hong, D. C. & Langer, J. S. (1986) Analytic theory for the selection of Saffman–Taylor fingers. Phys. Rev. Lett. 56, 2032–2035.Google Scholar
[18] Kessler, D. & Levine, H. (1986) The theory of Saffman–Taylor finger. Phys. Rev. A 33, 2634–2639.Google Scholar
[19] King, J. R. & Evans, J. D. (2005) Regularization by kinetic undercooling of blow-up in the ill-posed Stefan problem. SIAM J. Appl. Math. 65, 1677–1707.Google Scholar
[20] McCue, S. W., Hsieh, M., Moroney, T. J. & Nelson, M. I. (2011) Asymptotic and numerical results for a model of solvent-dependent drug diffusion through polymeric spheres. SIAM J. Appl. Math. 71, 2287–2311.Google Scholar
[21] Mclean, J. W. & Saffman, P. G. (1981) The effect of surface tension on the shape of fingers in a Hele–Shaw cell. J. Fluid Mech. 102, 455–469.Google Scholar
[22] Muskhelishvili, N. I. (1977) Singular Integral Equations, Noordhoff International Publishing, Gronigen, Netherlands.Google Scholar
[23] Olver, F. W. J. (1974) Asymtotics and Special Functions, Academic Press, New York.Google Scholar
[24] Pleshchinskii, N. B. & Reissig, M. (2002) Hele–Shaw flows with nonlinear kinetic undercooling regularization. Nonlinear Anal. 50, 191–203.Google Scholar
[25] Reissig, M., Rogosin, D. V. & Hubner, F. (1999) Analytical and numerical treatment of a complex model for Hele–Shaw moving boundary value problems with kinetic undercooling regularization. Eur. J. Appl. Math. 10, 561–579.Google Scholar
[26] Romero, L. A. (1981) The fingering problem in a Hele–Shaw cell, Ph.D thesis, California Institute of Technology.Google Scholar
[27] Saffman, P. G. (1986) Viscous fingering in Hele–shaw cells. J. Fluid Mech. 173, 73–94.Google Scholar
[28] Saffman, P. G. & Taylor, G. I. (1958) The penetration of a fluid into a porous medium of Hele–Shaw cell containing a more viscous fluid. Proc. R. Soc. London Ser. A. 245, 312–329.Google Scholar
[29] Saffman, P. G. (1959) Exact solutions for the growth of fingers from a flat interface between two fluids in a porous medium or Hele–Shaw cell. Q. J. Mech. Appl. Math. 12, 146–150.Google Scholar
[30] Shraiman, B. I. (1986) On velocity selection and the Saffman–Taylor problem. Phys. Rev. Lett. 56, 2028–2031.Google Scholar
[31] Tanveer, S. (1986) The effect of surface tension on the shape of a Hele–Shaw cell bubble. Phys. Fluids 29, 3537–3548.Google Scholar
[32] Tanveer, S. (1987) Analytic theory for the selection of symmetric Saffman–Taylor finger. Phys. Fluids 30, 1589–1605.Google Scholar
[33] Tanveer, S. (1991) Viscous Displacement in a Hele–Shaw cell. In: Segur, H., Tanveer, S. & Levine, H. (editors), Asymptotics Beyond all orders, Plenum, New York, pp. 131–153.Google Scholar
[34] Tanveer, S. (2000) Surprises in Viscous fingering. J. Fluid Mech. 409, 273–308.Google Scholar
[35] Tanveer, S. & Xie, X. (2003) Analyticity and nonexistence of classical steady Hele-Shaw fingers. Commun. Pure Appl. Math. 56, 353–402.Google Scholar
[36] Taylor, G. I. & Saffman, P. G. (1959) A note on the motion of bubbles in a Hele–Shaw cell and Porous medium. Q. J. Mech. Appl. Math. 17, 265–279.Google Scholar
[37] Vanden-Broeck, J. M. (1983) Fingers in a Hele–Shaw cell with surface tension. Phys. Fluids 26, 2033–2034.Google Scholar
[38] Xie, X. & Tanveer, S. (2003) Rigorous results in steady finger selection in viscous fingering. Arch. Rational Mech. Anal. 166, 219–286.Google Scholar
[39] Xie, X. (2016) Nonexistence of Steady Saffman–Taylor fingers by kinetic undercooling. Int. J. Evol. Equ. 10, 75–99.Google Scholar
[40] Zhuravlev, P. A. (1956) Zap. Leninger. Com. Inst. 33, 54–61 (in Russian).Google Scholar