Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-22T10:20:32.929Z Has data issue: false hasContentIssue false
  • English
  • Français

An orthogonality relation for 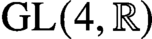$\mathrm {GL}(4, \mathbb R) $ (with an appendix by Bingrong Huang)

Part of: Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  07 June 2021

Dorian Goldfeld ,
Eric Stade  and
Michael Woodbury
Dorian Goldfeld
Affiliation:
Department of Mathematics, Columbia University, New York, NY10027, USA; E-mail: goldfeld@columbia.edu.
Eric Stade
Affiliation:
Department of Mathematics, University of Colorado, Bolder, CO80309, USA; E-mail: stade@colorado.edu.
Michael Woodbury
Affiliation:
Department of Mathematics, Brown University, Providence, RI02912, USA; E-mail: michael_woodbury@brown.edu.

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Orthogonality is a fundamental theme in representation theory and Fourier analysis. An orthogonality relation for characters of finite abelian groups (now recognized as an orthogonality relation on 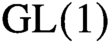$\mathrm {GL}(1)$) was used by Dirichlet to prove infinitely many primes in arithmetic progressions. Orthogonality relations for 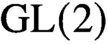$\mathrm {GL}(2)$ and 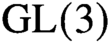$\mathrm {GL}(3)$ have been worked on by many researchers with a broad range of applications to number theory. We present here, for the first time, very explicit orthogonality relations for the real group 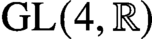$\mathrm {GL}(4, \mathbb R)$ with a power savings error term. The proof requires novel techniques in the computation of the geometric side of the Kuznetsov trace formula.

MSC classification

Primary: 11F55: Other groups and their modular and automorphic forms (several variables)
Secondary: 11F72: Spectral theory; Selberg trace formula
Type
Number Theory
Information
Forum of Mathematics, Sigma , Volume 9 , 2021 , e47
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BYCreative Common License - NCCreative Common License - ND
This is an Open Access article, distributed under the terms of the Creative Commons Attribution-NonCommercial-NoDerivatives licence (http://creativecommons.org/licenses/by-nc-nd/4.0/), which permits non-commercial re-use, distribution, and reproduction in any medium, provided the original work is unaltered and is properly cited. The written permission of Cambridge University Press must be obtained for commercial re-use or in order to create a derivative work.
Copyright
© The Author(s), 2021. Published by Cambridge University Press

References

Arthur, James, Eisenstein series and the trace formula, Automorphic forms, representations and $L$-functions (Proc. Sympos. Pure Math., Oregon State Univ., Corvallis, Ore. 1977), Part 1, Proc. Sympos. Pure Math., XXXIII, Amer. Math. Soc., Providence, R.I., 1979, pp. 253–274. MR 546601 (81b:10020)Google Scholar
Blomer, Valentin, Buttcane, Jack, and Raulf, Nicole, A Sato-Tate law for $\mathrm{GL}(3)$, Comment. Math. Helv. 89 (2014), no. 4, 895–919. MR 3284298CrossRefGoogle Scholar
Bump, Daniel, Friedberg, Solomon, and Goldfeld, Dorian, Poincaré series and Kloosterman sums for $\mathrm{SL}\left(3,Z\right)$, Acta Arith. 50 (1988), no. 1, 31–89. MR 945275 (89j:11047)CrossRefGoogle Scholar
Blomer, Valentin, Applications of the Kuznetsov formula on $\mathrm{GL}(3)$, Invent. Math. 194 (2013), no. 3, 673–729. MR 3127065CrossRefGoogle ScholarPubMed
Bruggeman, R. W., Fourier coefficients of cusp forms, Invent. Math. 45 (1978), no. 1, 1–18. MR 0472701CrossRefGoogle Scholar
Buttcane, Jack and Zhou, Fan, Plancherel Distribution of Satake Parameters of Maass Cusp Forms on GL3, Int. Math. Res. Not. IMRN (2020), no. 5, 1417–1444. MR 4073945CrossRefGoogle Scholar
Conrey, J. B., Duke, W., and Farmer, D. W., The distribution of the eigenvalues of Hecke operators, Acta Arith. 78 (1997), no. 4, 405–409. MR 1438595CrossRefGoogle Scholar
Deligne, P., Dualité, Cohomologie étale, Lecture Notes in Math., vol. 569, Springer, Berlin, 1977, pp. 154–167. MR 3727437Google Scholar
Dabrowski, Romuald and Fisher, Benji, A stationary phase formula for exponential sums over $\mathbf{Z}/{p}^m\mathbf{Z}$and applications to $\mathrm{GL}(3)$-Kloosterman sums, Acta Arith. 80 (1997), no. 1, 1–48. MR 1450415CrossRefGoogle Scholar
Dabrowski, Romuald and Reeder, Mark, Kloosterman sets in reductive groups, J. Number Theory 73 (1998), no. 2, 228–255. MR 1658031CrossRefGoogle Scholar
Friedberg, Solomon and Goldfeld, Dorian, Mellin transforms of Whittaker functions, Bull. Soc. Math. France 121 (1993), no. 1, 91–107. MR 1207245CrossRefGoogle Scholar
Finis, Tobias and Matz, Jasmin, On the asymptotics of hecke operators for reductive groups, 2019, arXiv:1905.09078.Google Scholar
Friedberg, Solomon, Poincaré series for $\mathrm{GL}(n)$: Fourier expansion, Kloosterman sums, and algebreo-geometric estimates, Math. Z. 196 (1987), no. 2, 165–188. MR 910824CrossRefGoogle Scholar
Goldfeld, Dorian and Hundley, Joseph, Automorphic representations and $L$-functions for the general linear group. Volume I, Cambridge Studies in Advanced Mathematics, vol. 129, Cambridge University Press, Cambridge, 2011, With exercises and a preface by Faber, Xander. MR 2807433Google Scholar
Goldfeld, Dorian and Kontorovich, Alex, On the determination of the Plancherel measure for Lebedev-Whittaker transforms on $\mathrm{GL}(n)$, Acta Arith. 155 (2012), no. 1, 15–26. MR 2982424CrossRefGoogle Scholar
Goldfeld, Dorian and Kontorovich, Alex, On the $\mathrm{GL}(3)$Kuznetsov formula with applications to symmetry types of families of $L$-functions, Automorphic representations and $L$-functions, Tata Inst. Fundam. Res. Stud. Math., vol. 22, Tata Inst. Fund. Res., Mumbai, 2013, pp. 263–310. MR 3156855Google Scholar
Goldfeld, Dorian and Li, Xiaoqing, A standard zero free region for Rankin-Selberg $L$-functions, Int. Math. Res. Not. IMRN (2018), no. 22, 7067–7136. MR 3878594CrossRefGoogle Scholar
Gelbart, Stephen S., Lapid, Erez M., and Sarnak, Peter, A new method for lower bounds of $L$-functions, C. R. Math. Acad. Sci. Paris 339 (2004), no. 2, 91–94. MR 2078295CrossRefGoogle Scholar
Goldfeld, Dorian, Miller, Stephen M., and Woodbury, Michael, A template method for fourier coefficients of langlands Eisenstein series. Rivista Di Matematica Della Universita Di Parma, Proceedings of the Second Symposium on Analytic Number Theory, Cetraro (Italy), 8-12 July 2019.Google Scholar
Goldfeld, Dorian, Notes on trace formulae for $\mathrm{SL}\left(2,R\right)$, http://www.math.columbia.edu/~goldfeld/TraceFormulae-4-12-2020.pdf.Google Scholar
Goldfeld, Dorian, Automorphic forms and $L$-functions for the group $\mathrm{GL}\left(n,\mathbf{R}\right)$, Cambridge Studies in Advanced Mathematics, vol. 99, Cambridge University Press, Cambridge, 2006, With an appendix by Broughan, Kevin A.. MR 2254662 (2008d:11046)Google Scholar
Goldfeld, Dorian, Automorphic forms and L-functions for the group $\mathrm{GL}\left(n,R\right)$, Cambridge Studies in Advanced Mathematics, vol. 99, Cambridge University Press, Cambridge, 2015, With an appendix by Broughan, Kevin A., Paperback edition of the 2006 original. MR 3468028Google Scholar
Guerreiro, João, An orthogonality relation for a thin family of $\mathrm{GL}(3)$Maass forms, Int. J. Number Theory 11 (2015), no. 8, 2277–2294. MR 3420744CrossRefGoogle Scholar
Humphries, Peter and Brumley, Farrell, Standard zero-free regions for Rankin-Selberg $L$-functions via sieve theory, Math. Z. 292 (2019), no. 3-4, 1105–1122. MR 3980284CrossRefGoogle Scholar
Hoffstein, Jeffrey and Lockhart, Paul, Coefficients of Maass forms and the Siegel zero, Ann. of Math. (2) 140 (1994), no. 1, 161–181, With an appendix by Dorian Goldfeld, Hoffstein and Daniel Lieman. MR 1289494CrossRefGoogle Scholar
Hoffstein, Jeffrey and Ramakrishnan, Dinakar, Siegel zeros and cusp forms, Internat. Math. Res. Notices (1995), no. 6, 279–308. MR 1344349Google Scholar
Jacquet, Hervé, Fonctions de Whittaker associées aux groupes de Chevalley, Bull. Soc. Math. France 95 (1967), 243–309. MR 0271275CrossRefGoogle Scholar
Jana, Subhajit, Applications of analytic newvectors for gl( $r$), 2020, arXiv:2001.09640v2.Google Scholar
Kim, Henry H., The residual spectrum of ${G}_2$, Canad. J. Math. 48 (1996), no. 6, 1245–1272. MR 1426903CrossRefGoogle Scholar
Langlands, Robert P., On the functional equations satisfied by Eisenstein series, Lecture Notes in Mathematics, Vol. 544, Springer-Verlag, Berlin-New York, 1976. MR 0579181CrossRefGoogle Scholar
Lapid, Erez M. and Mao, Zhengyu, Local Rankin-Selberg integrals for representations, 2018, arXiv:1806.10528.Google Scholar
Luo, Wenzhi, Rudnick, Zeév, and Sarnak, Peter, On the generalized Ramanujan conjecture for $\mathrm{GL}(n)$, Automorphic forms, automorphic representations, and arithmetic (Fort Worth, TX, 1996), Proc. Sympos. Pure Math., vol. 66, Amer. Math. Soc., Providence, RI, 1999, pp. 301–310. MR 1703764CrossRefGoogle Scholar
Miller, Stephen D., The highest lowest zero and other applications of positivity, Duke Math. J. 112 (2002), no. 1, 83–116. MR 1890648CrossRefGoogle Scholar
Moreno, Carlos J., Analytic proof of the strong multiplicity one theorem, Amer. J. Math. 107 (1985), no. 1, 163–206. MR 778093CrossRefGoogle Scholar
Matz, Jasmin and Templier, Nicolas, Sato-tate equidistribution for families of hecke-maass forms on sl(n,r)/so(n), 2015, arXiv:1505.07285.Google Scholar
Mœglin, C. and Waldspurger, J.-L., Spectral decomposition and Eisenstein series, Cambridge Tracts in Mathematics, vol. 113, Cambridge University Press, Cambridge, 1995, Une paraphrase de l’Écriture [A paraphrase of Scripture]. MR 1361168CrossRefGoogle Scholar
Sarnak, Peter, Statistical properties of eigenvalues of the Hecke operators, Analytic number theory and Diophantine problems (Stillwater, OK, 1984), Progr. Math., vol. 70, Birkhäuser Boston, Boston, MA, 1987, pp. 321–331. MR 1018385Google Scholar
Sarnak, Peter, Nonvanishing of $L$-functions on $\mathfrak{R}(s)=1$, Contributions to automorphic forms, geometry, and number theory, Johns Hopkins Univ. Press, Baltimore, MD, 2004, pp. 719–732. MR 2058625Google Scholar
Serre, Jean-Pierre, Répartition asymptotique des valeurs propres de l’opérateur de Hecke ${T}_p$, J. Amer. Math. Soc. 10 (1997), no. 1, 75–102. MR 1396897CrossRefGoogle Scholar
Shahidi, Freydoon, Eisenstein series and automorphic $L$-functions, American Mathematical Society Colloquium Publications, vol. 58, American Mathematical Society, Providence, RI, 2010. MR 2683009CrossRefGoogle Scholar
Shin, Sug Woo and Templier, Nicolas, Sato-Tate theorem for families and low-lying zeros of automorphic $L$-functions, Invent. Math. 203 (2016), no. 1, 1–177, Appendix A by Kottwitz, Robert, and Appendix B by Cluckers, Raf, Gordon, Julia and Halupczok, Immanuel. MR 3437869CrossRefGoogle Scholar
Stade, Eric and Trinh, Tien D., Recurrence relations for Mellin transforms of $\mathrm{GL}\left(n,\mathbb{R}\right)$Whittaker functions, J. Funct. Anal. 280 (2021).CrossRefGoogle Scholar
Stade, Eric, Mellin transforms of Whittaker functions on $\mathrm{GL}\left(4,R\right)$and $\mathrm{GL}\left(4,C\right)$, Manuscripta Math. 87 (1995), no. 4, 511–526. MR 1344605CrossRefGoogle Scholar
Stade, Eric, Mellin transforms of $\mathrm{GL}\left(n,\mathbb{R}\right)$Whittaker functions, Amer. J. Math. 123 (2001), no. 1, 121–161. MR 1827280CrossRefGoogle Scholar
Stade, Eric, Archimedean $L$-factors on $\mathrm{GL}(n)\times \mathrm{GL}(n)$and generalized Barnes integrals, Israel J. Math. 127 (2002), 201–219. MR 1900699CrossRefGoogle Scholar
Stevens, Glenn, Poincaré series on $\mathrm{GL}(r)$and Kloostermann sums, Math. Ann. 277 (1987), no. 1, 25–51. MR 884644CrossRefGoogle Scholar
Vinogradov, I. M., A new estimate of the function $\zeta \left(1+\mathrm{it}\right)$, Izv. Akad. Nauk SSSR. Ser. Mat. 22 (1958), 161–164. MR 0103861Google Scholar
Vogan, David A. Jr., Gel’ fand-Kirillov dimension for Harish-Chandra modules, Invent. Math. 48 (1978), no. 1, 75–98. MR 506503CrossRefGoogle Scholar
Weil, André, On some exponential sums, Proc. Nat. Acad. Sci. U. S. A. 34 (1948), 204–207. MR 0027006CrossRefGoogle ScholarPubMed
Zhou, Fan, Sato-Tate Problem for GL(3), ProQuest LLC, Ann Arbor, MI, 2013, PhD thesis, Columbia University. MR 3153224Google Scholar
Zhou, Fan, Weighted Sato-Tate vertical distribution of the Satake parameter of Maass forms on $\mathrm{PGL}(N)$, Ramanujan J. 35 (2014), no. 3, 405–425. MR 3274875CrossRefGoogle Scholar