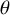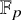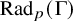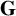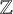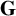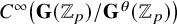1 Introduction
The main result of this paper is the following:
Theorem A see §10.1 below.
There is an increasing function
![]() $C^{\mathit{fin}}:\mathbb N\to \mathbb N$
such that, for any
$C^{\mathit{fin}}:\mathbb N\to \mathbb N$
such that, for any
-
• Odd prime p,
-
• Positive integer d,
-
• Finite group
 $\Gamma $
,
$\Gamma $
, -
• Normal p-subgroup
 $N\lhd \Gamma $
,
$N\lhd \Gamma $
, -
• Embedding
 $\Gamma /N \hookrightarrow GL_d(\mathbb {F}_p)$
,
$\Gamma /N \hookrightarrow GL_d(\mathbb {F}_p)$
, -
• Involution
 $\theta $
of
$\theta $
of
 $\Gamma $
,
$\Gamma $
, -
• Irreducible representation
 $\rho $
of
$\rho $
of
 $\Gamma $
,
$\Gamma $
,
the space
![]() $\rho ^{\Gamma ^ \theta }$
of
$\rho ^{\Gamma ^ \theta }$
of
![]() $\Gamma ^ \theta $
-invariant vectors of
$\Gamma ^ \theta $
-invariant vectors of
![]() $\rho $
has dimension at most
$\rho $
has dimension at most
![]() $C^{\mathit{fin}}(d)$
.
$C^{\mathit{fin}}(d)$
.
As a corollary, we deduce the following
Corollary B (see §10.1 below).
For every integer d, there is an integer
![]() $\Lambda $
such that, if
$\Lambda $
such that, if
-
• p is an odd prime,
-
• F is a purely ramified extension of
 $\mathbb {Q}_p$
,
$\mathbb {Q}_p$
, -
•
 $\mathbf {G}$
is a connected linear algebraic group over F whose reductive quotient has dimension at most d,
$\mathbf {G}$
is a connected linear algebraic group over F whose reductive quotient has dimension at most d, -
•
 $K \subset \mathbf {G}(F)$
is a compact subgroup,
$K \subset \mathbf {G}(F)$
is a compact subgroup, -
•
 $\theta $
is an involution of K,
$\theta $
is an involution of K, -
•
 $\rho $
is an irreducible representation of K,
$\rho $
is an irreducible representation of K,
then
Remark 1.0.1. An important special case of Theorem A is where
![]() $\Gamma =\mathbf {G}(\mathbb {Z} / p^n)$
, when
$\Gamma =\mathbf {G}(\mathbb {Z} / p^n)$
, when
![]() $\mathbf {G}$
is a semisimple group scheme and
$\mathbf {G}$
is a semisimple group scheme and
![]() $\theta $
is the restriction of an algebraic involution. The uniformity in the involution
$\theta $
is the restriction of an algebraic involution. The uniformity in the involution
![]() $\theta $
is not essential. The case
$\theta $
is not essential. The case
![]() $n=1$
(and p varies) was proved in [Reference Aizenbud and AvniAA19, Reference ShechterShe]. The case when p is fixed and n varies is much easier than the general result and can be directly deduced from Corollary 5.0.5.
$n=1$
(and p varies) was proved in [Reference Aizenbud and AvniAA19, Reference ShechterShe]. The case when p is fixed and n varies is much easier than the general result and can be directly deduced from Corollary 5.0.5.
1.1 Background and motivation
Let G be a group and let X be a transitive G-space. A basic problem of representation theory is to compute the multiplicities with which irreducible representations of G appear in the space of functions on X. This problem can be studied in several settings. In each setting, one considers a different kind of function space. For an example in the algebraic setting, if G is a connected reductive algebraic group over
![]() $\mathbb {C}$
and X is a spherical G-variety (this means that the Borel subgroup of G has an open orbit in X), then
$\mathbb {C}$
and X is a spherical G-variety (this means that the Borel subgroup of G has an open orbit in X), then
![]() $\mathbb {C}[X]$
is multiplicity-free as a G-representation.
$\mathbb {C}[X]$
is multiplicity-free as a G-representation.
Multiplicities for spherical G-varieties are of great interest in other settings. In non-algebraic settings, these multiplicities may be greater than one. One has the following conjecture:
Conjecture C. Let
![]() $\mathbf {G}$
be a reductive group scheme over
$\mathbf {G}$
be a reductive group scheme over
![]() $\mathbb {Z}$
and let
$\mathbb {Z}$
and let
![]() $\mathbf {X}$
be a
$\mathbf {X}$
be a
![]() $\mathbf {G}$
-scheme. Assume that
$\mathbf {G}$
-scheme. Assume that
![]() $\mathbf {X}(\mathbb {C})$
is a spherical
$\mathbf {X}(\mathbb {C})$
is a spherical
![]() $\mathbf {G}(\mathbb {C})$
-space. Then there is an integer C such that, if F is a local field of large enough characteristic and
$\mathbf {G}(\mathbb {C})$
-space. Then there is an integer C such that, if F is a local field of large enough characteristic and
![]() $\rho $
is a smooth, admissible and irreducible representation
$\rho $
is a smooth, admissible and irreducible representation
![]() $\mathbf {G}(F)$
, then
$\mathbf {G}(F)$
, then
One can study variants of this conjecture in various levels.
-
• The most basic level is when both F and
 $\rho $
are fixed. This case was mostly done. See [Reference van den BanvdB87, Reference DelormeDel10, Reference Sakellaridis and VenkateshSV17].
$\rho $
are fixed. This case was mostly done. See [Reference van den BanvdB87, Reference DelormeDel10, Reference Sakellaridis and VenkateshSV17]. -
• The next level is when F is fixed and C is required to be independent of
 $\rho $
. The main known results in this level are for the archimedian case. See [Reference van den BanvdB87, Reference Kobayashi and OshimaKO13, Reference Krötz and SchlichtkrullKS16, Reference Aizenbud, Gourevitch and MinchenkoAGM16].
$\rho $
. The main known results in this level are for the archimedian case. See [Reference van den BanvdB87, Reference Kobayashi and OshimaKO13, Reference Krötz and SchlichtkrullKS16, Reference Aizenbud, Gourevitch and MinchenkoAGM16]. -
• The last level is the full conjecture where both F and
 $\rho $
vary. Here, the only known cases are where the spherical spaces are multiplicity free (i.e., Gelfand pairs) and related situations. Although there are many known Gelfand pairs (see, for example, [Reference Gel’fand and KazhdanGK75, Reference ShalikaSha74, Reference van DijkvD86, Reference FlickerFli91, Reference Bosman and van DijkBvD94, Reference NienNie06, Reference YakimovaYak05, Reference Aizenbud, Gourevitch, Rallis and SchiffmannAGRS10, Reference Aizenbud, Gourevitch and SayagAGS08, Reference Offen and SayagOS08, Reference Aizenbud and GourevitchAG09b, Reference Aizenbud and GourevitchAG09a, Reference Aizenbud and GourevitchAG10, Reference Aizenbud, Avni and GourevitchAAG12, Reference ZhangZha10, Reference Jiang, Sun and ZhuJSZ10, Reference Jiang, Sun and ZhuJSZ11, Reference Aizenbud and SayagAS12, Reference Aizenbud, Gourevitch and JacquetAGJ09, Reference Aizenbud and GourevitchAG12, Reference Sun and ZhuSZ12, Reference AizenbudAiz13, Reference Chen and SunCS15, Reference CarmeliCar, Reference RubioRub], and the reference therein), general spherical spaces are not multiplicity free.
$\rho $
vary. Here, the only known cases are where the spherical spaces are multiplicity free (i.e., Gelfand pairs) and related situations. Although there are many known Gelfand pairs (see, for example, [Reference Gel’fand and KazhdanGK75, Reference ShalikaSha74, Reference van DijkvD86, Reference FlickerFli91, Reference Bosman and van DijkBvD94, Reference NienNie06, Reference YakimovaYak05, Reference Aizenbud, Gourevitch, Rallis and SchiffmannAGRS10, Reference Aizenbud, Gourevitch and SayagAGS08, Reference Offen and SayagOS08, Reference Aizenbud and GourevitchAG09b, Reference Aizenbud and GourevitchAG09a, Reference Aizenbud and GourevitchAG10, Reference Aizenbud, Avni and GourevitchAAG12, Reference ZhangZha10, Reference Jiang, Sun and ZhuJSZ10, Reference Jiang, Sun and ZhuJSZ11, Reference Aizenbud and SayagAS12, Reference Aizenbud, Gourevitch and JacquetAGJ09, Reference Aizenbud and GourevitchAG12, Reference Sun and ZhuSZ12, Reference AizenbudAiz13, Reference Chen and SunCS15, Reference CarmeliCar, Reference RubioRub], and the reference therein), general spherical spaces are not multiplicity free.
Our motivation for Corollary B is the following strategy for proving Conjecture C:
-
1. Prove a variant of Conjecture C when F ranges over the collection of finite fields.
-
2. Deduce from (1) a variant of Conjecture C when F ranges over the collection of rings of integers in local fields.
-
3. Deduce Conjecture C from (2).
Step (1) was done in [Reference Aizenbud and AvniAA19, Reference ShechterShe]. Corollary B implies Step (2) under certain conditions:
Corollary D (see §10.1 below).
Let
![]() $\mathbf {G}$
be a reductive group scheme over
$\mathbf {G}$
be a reductive group scheme over
![]() $\mathbb {Z}$
, let
$\mathbb {Z}$
, let
![]() $\theta $
be an involution of
$\theta $
be an involution of
![]() $\mathbf {G}$
and let
$\mathbf {G}$
and let
![]() $\mathbf {X}=\mathbf {G} / \mathbf {G} ^ \theta $
be the corresponding symmetric space. Then there is an integer C such that, for every odd prime p and every irreducible representation
$\mathbf {X}=\mathbf {G} / \mathbf {G} ^ \theta $
be the corresponding symmetric space. Then there is an integer C such that, for every odd prime p and every irreducible representation
![]() $\rho $
of
$\rho $
of
![]() $\mathbf {G}(\mathbb {Z}_p)$
,
$\mathbf {G}(\mathbb {Z}_p)$
,
1.2 The Larsen–Pink theorem
A central ingredient in the proof of Theorem A is a theorem of [Reference Larsen and PinkLP11] roughly stating that finite subgroups of
![]() $\operatorname {\mathrm {GL}}_d(\mathbb {F}_p)$
are close to groups of
$\operatorname {\mathrm {GL}}_d(\mathbb {F}_p)$
are close to groups of
![]() $\mathbb {F}_p$
-points of connected algebraic subgroups of
$\mathbb {F}_p$
-points of connected algebraic subgroups of
![]() $\operatorname {\mathrm {GL}}_d$
. We use the Larsen–Pink theorem in several ways:
$\operatorname {\mathrm {GL}}_d$
. We use the Larsen–Pink theorem in several ways:
-
• The Larsen–Pink theorem attaches an algebraic group of
 $\operatorname {\mathrm {GL}}_n$
to finite subgroups of
$\operatorname {\mathrm {GL}}_n$
to finite subgroups of
 $\operatorname {\mathrm {GL}}_n(\mathbb {F}_p)$
, and we prove Theorem A by induction on the dimension on this algebraic group. In particular, the Larsen–Pink theorem implies that the lengths of decreasing chains of perfect subgroups of
$\operatorname {\mathrm {GL}}_n(\mathbb {F}_p)$
, and we prove Theorem A by induction on the dimension on this algebraic group. In particular, the Larsen–Pink theorem implies that the lengths of decreasing chains of perfect subgroups of
 $\operatorname {\mathrm {GL}}_d(\mathbb {F}_p)$
are bounded when we vary p.
$\operatorname {\mathrm {GL}}_d(\mathbb {F}_p)$
are bounded when we vary p. -
• It allows us to reduce statements about finite groups with no normal p-subgroups to finite groups of Lie type. We use this to prove the main theorem for groups with trivial p-radical (see §8) and to get bounds on various cohomology groups in §6 and §7.
We discuss the Larsen–Pink theorem and its applications in §4.
1.3 Sketch of the proof of Theorem A
To prove Theorem A, we analyze the extreme cases
![]() $N=\Gamma $
and
$N=\Gamma $
and
![]() $N=1$
, and we use Clifford’s theory to deduce the general cases from them. The main difficulty is to control the multiplicities when describing a representation using Clifford’s theory.
$N=1$
, and we use Clifford’s theory to deduce the general cases from them. The main difficulty is to control the multiplicities when describing a representation using Clifford’s theory.
We now sketch the proof of Theorem A. We first analyze the case of groups with odd order. The analysis is based on the simple observation that every element in such a group has a unique square root. We prove a Gelfand property (i.e., multiplicity one property) for symmetric pairs of such groups. In addition, we prove a necessary condition (related to conjectures of Lapid and Prasad [Reference GlazerGla18, Reference PrasadPra]) for a representation of a group G of odd order to be distinguished with respect to a symmetric subgroup of G. Finally, we show that the first cohomology of
![]() $S_2$
with coefficients in groups of odd order vanishes. We treat this case in §5.
$S_2$
with coefficients in groups of odd order vanishes. We treat this case in §5.
Next, we analyze the case of a group with a trivial p-radical. Here, we prove a twisted version of the main theorem. Using the Larsen-Pink theorem, we reduce this case to the case of finite groups of Lie type, where we apply a similar reasoning as in [Reference Aizenbud and AvniAA19, Reference ShechterShe]. We treat this case in §8 and Appendix A.
For the general case, we introduce the following invariant of a group
![]() $\Gamma $
:
$\Gamma $
:
![]() $\overline {\mathrm {rd}}_p(\Gamma )$
is the smallest possible dimension of a connected reductive group
$\overline {\mathrm {rd}}_p(\Gamma )$
is the smallest possible dimension of a connected reductive group
![]() $\mathbf {G}$
such that
$\mathbf {G}$
such that
![]() $\Gamma / \operatorname {\mathrm {Rad}}_p(\Gamma ) \subseteq \mathbf {G}(\mathbb {F}_p)$
. Since, in the notations of Theorem A,
$\Gamma / \operatorname {\mathrm {Rad}}_p(\Gamma ) \subseteq \mathbf {G}(\mathbb {F}_p)$
. Since, in the notations of Theorem A,
![]() $\overline {\mathrm {rd}}_p(\Gamma ) \leq d^2$
, it is enough to bound
$\overline {\mathrm {rd}}_p(\Gamma ) \leq d^2$
, it is enough to bound
![]() ${\operatorname {dim}} \rho ^{\Gamma ^ \theta }$
in terms of
${\operatorname {dim}} \rho ^{\Gamma ^ \theta }$
in terms of
![]() $\overline {\mathrm {rd}}_p(\Gamma )$
. This is done by induction on
$\overline {\mathrm {rd}}_p(\Gamma )$
. This is done by induction on
![]() $\overline {\mathrm {rd}}_p(\Gamma )$
. In the rest of the section, we describe the induction step.
$\overline {\mathrm {rd}}_p(\Gamma )$
. In the rest of the section, we describe the induction step.
Clifford theory implies that there is a group
![]() $\Delta $
satisfying
$\Delta $
satisfying
![]() $\operatorname {\mathrm {Rad}}_p(\Gamma ) < \Delta <\Gamma $
and an irreducible representation
$\operatorname {\mathrm {Rad}}_p(\Gamma ) < \Delta <\Gamma $
and an irreducible representation
![]() $\sigma $
of
$\sigma $
of
![]() $\Delta $
such that
$\Delta $
such that
-
•
 $\rho =Ind_\Delta ^\Gamma (\sigma )$
.
$\rho =Ind_\Delta ^\Gamma (\sigma )$
. -
•
 $\sigma |_{\operatorname {\mathrm {Rad}}_p(\Gamma )} $
is isotypic.
$\sigma |_{\operatorname {\mathrm {Rad}}_p(\Gamma )} $
is isotypic.
By Mackey’s formula, the multiplicity
![]() ${\operatorname {dim}} \rho ^{\Gamma ^\theta }$
is a sum of multiplicities of
${\operatorname {dim}} \rho ^{\Gamma ^\theta }$
is a sum of multiplicities of
![]() $\sigma $
in various transitive
$\sigma $
in various transitive
![]() $\Delta $
-sets. A priori, the number of transitive
$\Delta $
-sets. A priori, the number of transitive
![]() $\Delta $
-sets that might contribute to
$\Delta $
-sets that might contribute to
![]() ${\operatorname {dim}} \rho ^{\Gamma ^\theta }$
is
${\operatorname {dim}} \rho ^{\Gamma ^\theta }$
is
![]() $|\Gamma ^\theta \backslash \Gamma /\Delta |$
, which is unbounded. We use the Lapid–Prasad criterion to bound the number of subgroups of
$|\Gamma ^\theta \backslash \Gamma /\Delta |$
, which is unbounded. We use the Lapid–Prasad criterion to bound the number of subgroups of
![]() $\Delta $
whose contribution is nonzero by
$\Delta $
whose contribution is nonzero by
![]() $|H^1(S_2,\Delta )|$
, which we can bound.
$|H^1(S_2,\Delta )|$
, which we can bound.
To bound the individual contribution of a transitive
![]() $\Delta $
-set, we analyze two possibilities:
$\Delta $
-set, we analyze two possibilities:
-
•
 $\operatorname {\mathrm {Rad}}_p(\Delta )=\operatorname {\mathrm {Rad}}_p(\Gamma )$
.
$\operatorname {\mathrm {Rad}}_p(\Delta )=\operatorname {\mathrm {Rad}}_p(\Gamma )$
.In this case, the bound on
 implies that, for large p, the representation
implies that, for large p, the representation
 $\sigma $
is a tensor product of a representation
$\sigma $
is a tensor product of a representation
 $\sigma _1$
that is trivial on
$\sigma _1$
that is trivial on
 $\operatorname {\mathrm {Rad}}_p(\Delta )$
and a representation
$\operatorname {\mathrm {Rad}}_p(\Delta )$
and a representation
 $\sigma _2$
that is irreducible when restricted to
$\sigma _2$
that is irreducible when restricted to
 $\operatorname {\mathrm {Rad}}_p(\Delta )$
. The multiplicity of
$\operatorname {\mathrm {Rad}}_p(\Delta )$
. The multiplicity of
 $\sigma _2$
is at most one since
$\sigma _2$
is at most one since
 $\operatorname {\mathrm {Rad}}_p(\Delta )$
has odd order. The bound on the multiplicity
$\operatorname {\mathrm {Rad}}_p(\Delta )$
has odd order. The bound on the multiplicity
 $\sigma _1$
follows from the analysis of the case with trivial p-radical mentioned above. At this point of the argument, we need to bound twisted multiplicities of representations of
$\sigma _1$
follows from the analysis of the case with trivial p-radical mentioned above. At this point of the argument, we need to bound twisted multiplicities of representations of
 $\Delta / \operatorname {\mathrm {Rad}}_p(\Delta )$
rather than usual multiplicities. The reason is that the one-dimensional multiplicity space obtained for
$\Delta / \operatorname {\mathrm {Rad}}_p(\Delta )$
rather than usual multiplicities. The reason is that the one-dimensional multiplicity space obtained for
 $\operatorname {\mathrm {Rad}}_p(\Delta )$
manifests itself as a twist here.
$\operatorname {\mathrm {Rad}}_p(\Delta )$
manifests itself as a twist here. -
•
 $\operatorname {\mathrm {Rad}}_p(\Delta )\neq \operatorname {\mathrm {Rad}}_p(\Gamma )$
.
$\operatorname {\mathrm {Rad}}_p(\Delta )\neq \operatorname {\mathrm {Rad}}_p(\Gamma )$
.In this case, the Larsen–Pink Theorem implies that there is subgroup of bounded index
 $\Delta ^\circ \lhd \Delta $
such that
$\Delta ^\circ \lhd \Delta $
such that
 $\overline {\mathrm {rd}}(\Delta ^\circ )<\overline {\mathrm {rd}}(\Gamma )$
. We deduce the required bound from the induction assumption.
$\overline {\mathrm {rd}}(\Delta ^\circ )<\overline {\mathrm {rd}}(\Gamma )$
. We deduce the required bound from the induction assumption.
1.4 Complication related to the action of
 ${S_2}$
${S_2}$
The sketch above overlooks one technical point. Namely, although the Larsen–Pink theorem was proved for groups, we need it for symmetric pairs or, equivalently, in the
![]() $S_2$
-equivariant setting. One way around this difficulty is to embed
$S_2$
-equivariant setting. One way around this difficulty is to embed
![]() $\Gamma $
into
$\Gamma $
into
![]() $\Gamma \times \Gamma $
using the graph of
$\Gamma \times \Gamma $
using the graph of
![]() $\theta $
. Under this embedding,
$\theta $
. Under this embedding,
![]() $\theta $
becomes the flip
$\theta $
becomes the flip
![]() $(x,y) \mapsto (y,x)$
, which clearly extends to the ambient algebraic group. This way is implemented in Lemma 2.2.3 below. The drawback of this method is that it doubles the dimension of the ambient algebraic group, so it is not suitable for induction. So, in some parts of the argument, we use a different method: We use an iterative procedure, based on the Larsen-Pink Theorem that allows us to replace (without increasing the value of
$(x,y) \mapsto (y,x)$
, which clearly extends to the ambient algebraic group. This way is implemented in Lemma 2.2.3 below. The drawback of this method is that it doubles the dimension of the ambient algebraic group, so it is not suitable for induction. So, in some parts of the argument, we use a different method: We use an iterative procedure, based on the Larsen-Pink Theorem that allows us to replace (without increasing the value of
![]() $\overline {\mathrm {rd}}_p$
) a subgroup of bounded index with a smaller
$\overline {\mathrm {rd}}_p$
) a subgroup of bounded index with a smaller
![]() $S_2$
-invariant subgroup, also of bounded index. We implement this procedure in Lemma 4.1.1 below. This procedure is very costly in terms of the bounds on the indexes, and it is one of the main reasons why our bound on the multiplicities is very large.
$S_2$
-invariant subgroup, also of bounded index. We implement this procedure in Lemma 4.1.1 below. This procedure is very costly in terms of the bounds on the indexes, and it is one of the main reasons why our bound on the multiplicities is very large.
1.5 Limitation of our result
-
• Our bounds on the multiplicities are given in terms of an embedding into a group of
 $\mathbb {F}_p$
-points rather than a group of
$\mathbb {F}_p$
-points rather than a group of
 $\overline {\mathbb {F}_p}$
-points. Therefore, we do not bound the multiplicity of symmetric pairs with
$\overline {\mathbb {F}_p}$
-points. Therefore, we do not bound the multiplicity of symmetric pairs with
 $G=\mathbf {G}(O_F)$
when F ranges over all extensions of a given local non-archimedean field (of course, if the degree
$G=\mathbf {G}(O_F)$
when F ranges over all extensions of a given local non-archimedean field (of course, if the degree
 $[O_F/\mathfrak {m}_F : \mathbb {F}_p]$
is fixed, we do get uniform bounds). The reason is that, unlike
$[O_F/\mathfrak {m}_F : \mathbb {F}_p]$
is fixed, we do get uniform bounds). The reason is that, unlike
 $\mathbf {G}(\mathbb {F}_p)$
, the group
$\mathbf {G}(\mathbb {F}_p)$
, the group
 $\mathbf {G}( \overline {\mathbb {F}_p})$
has decreasing chains of perfect subgroups of arbitrary length. For this reason, we do not conjecture that Theorem A holds if we replace
$\mathbf {G}( \overline {\mathbb {F}_p})$
has decreasing chains of perfect subgroups of arbitrary length. For this reason, we do not conjecture that Theorem A holds if we replace
 $\mathbb {F}_p$
with
$\mathbb {F}_p$
with
 $\overline {\mathbb {F}_p}$
.
$\overline {\mathbb {F}_p}$
. -
• The bounds on the multiplicities we obtain are extremely large. We did not try to optimize the bounds since our argument cannot prove any reasonable bounds.
-
• In the general case, we only bound usual multiplicities and not twisted ones. The reason is that our analysis of odd order groups does not work well in the twisted case. We do not expect any problems with the twisted Gelfand property, and we also think that it will be easy to obtain a criterion for twisted distinction. However, this criterion will be different from the untwisted, so the number of symmetric subgroups of
 $\Delta $
contributing to the multiplicity will not be the size of any homology but rather some other number that we do not know how to bound. It would be interesting to resolve the twisted case, especially since we use bounds on twisted multiplicities in the case of trivial p-radical in order to bound the usual multiplicities in the general case.
$\Delta $
contributing to the multiplicity will not be the size of any homology but rather some other number that we do not know how to bound. It would be interesting to resolve the twisted case, especially since we use bounds on twisted multiplicities in the case of trivial p-radical in order to bound the usual multiplicities in the general case.
1.6 Structure of the paper
In §2, we fix notations and formulate our main result. See Theorem 2.3.1. In particular, we introduce an invariant
![]() $\overline {\mathrm {rd}}_p$
to measure ‘dimension’ of a finite group. See Definition 2.2.1.
$\overline {\mathrm {rd}}_p$
to measure ‘dimension’ of a finite group. See Definition 2.2.1.
In §3, we recall some group theoretic facts.
In §4, we quote the Larsen–Pink Theorem and deduce two corollaries that we will use in the paper: Corollary 4.0.13 and Corollary 4.1.2.
In §5, we treat the case of groups of odd order. In this case, we prove a stronger form of the main result along with some other results for this special case. See Lemma 5.0.2 and Corollary 5.0.5.
In §6, we bound the size of the first cohomology group of
![]() $S_2$
with coefficients in a finite group
$S_2$
with coefficients in a finite group
![]() $\Gamma $
in terms of
$\Gamma $
in terms of
![]() $\overline {\mathrm {rd}}_p(\Gamma )$
. See Corollary 6.0.6.
$\overline {\mathrm {rd}}_p(\Gamma )$
. See Corollary 6.0.6.
In §7, we prove a vanishing result for
![]() $H^2(\Gamma ,\mathbb {Z} / p^n)$
, where
$H^2(\Gamma ,\mathbb {Z} / p^n)$
, where
![]() $\Gamma $
is a finite group, assuming p is large enough with respect to
$\Gamma $
is a finite group, assuming p is large enough with respect to
![]() $\overline {\mathrm {rd}}_p(\Gamma )$
. See Proposition 7.0.2.
$\overline {\mathrm {rd}}_p(\Gamma )$
. See Proposition 7.0.2.
In §8, we prove a twisted version of the main result for the case of groups with trivial p-radical. See Corollary 8.0.5.
In §9, we recall some basic results of Clifford theory which are needed in our proof.
In §10, we prove our main result, Theorem 2.3.1. In §§10.1, we deduce Theorem A and Corollary B from Theorem 2.3.1.
In Appendix A, we prove a twisted version of the main result for finite groups of Lie type. The argument is an adaptation (to the twisted case) of [Reference ShechterShe].
In Appendix B, we construct a family of symmetric pairs of reductive groups that includes all symmetric pairs of reductive groups of a given dimension over all finite fields; see Lemma 3.2.1. We use this construction in §4 in order to express the bounds given by the Larsen–Pink theorem in terms of
![]() $\overline {\mathrm {rd}}_p$
.
$\overline {\mathrm {rd}}_p$
.
2 Conventions, notations and reformulation of the main result
2.1 Conventions
-
• By a finite symmetric pair, we will mean a pair
 $(\Gamma ,\theta )$
, where
$(\Gamma ,\theta )$
, where
 $\Gamma $
is a finite group and
$\Gamma $
is a finite group and
 $\theta $
is a (possibly trivial) involution of
$\theta $
is a (possibly trivial) involution of
 $\Gamma $
. For a symmetric pair
$\Gamma $
. For a symmetric pair
 $(\Gamma ,\theta )$
, we get a symmetric subgroup
$(\Gamma ,\theta )$
, we get a symmetric subgroup
 $\Gamma ^\theta \subset \Gamma $
, a symmetric space
$\Gamma ^\theta \subset \Gamma $
, a symmetric space
 $\Gamma /\Gamma ^\theta $
and an action of
$\Gamma /\Gamma ^\theta $
and an action of
 $S_2$
on
$S_2$
on
 $\Gamma $
.
$\Gamma $
. -
• For a group G, we denote the derived subgroup of G by
 $G'$
and the center of G by
$G'$
and the center of G by
 $Z(G)$
. If
$Z(G)$
. If
 $\mathbf {G}$
is an algebraic group, we denote the connected component of identity in
$\mathbf {G}$
is an algebraic group, we denote the connected component of identity in
 $\mathbf {G}$
by
$\mathbf {G}$
by
 $\mathbf {G} ^\circ $
.
$\mathbf {G} ^\circ $
. -
• All schemes considered in this paper are assumed to be of finite type over Noetherian base schemes.
-
• By a simple algebraic group, we mean a connected algebraic group whose Lie algebra is simple.
-
• Throughout the paper, we will formulate and prove several lemmas that assert the existence of increasing functions
 $\mathbb N\to \mathbb N$
satisfying certain conditions. Each of those lemmas will give the corresponding function a distinct notation. It is implied that, after each such lemma, we fix such a function and use that notation to refer to it. The choices of such functions are not unique, but the only effect of a different choice is different bounds. Since we just claim the existence of bounds, this is irrelevant to us.
$\mathbb N\to \mathbb N$
satisfying certain conditions. Each of those lemmas will give the corresponding function a distinct notation. It is implied that, after each such lemma, we fix such a function and use that notation to refer to it. The choices of such functions are not unique, but the only effect of a different choice is different bounds. Since we just claim the existence of bounds, this is irrelevant to us. -
• We will usually use capital boldface letters to denote varieties, capital calligraphic letters to denote schemes, and capital gothic letters to denote sheaves.
2.2 Notations
We will use the following invariants of a finite group.
Definition 2.2.1. Let
![]() $\Gamma $
be a finite group and p be a prime.
$\Gamma $
be a finite group and p be a prime.
-
1. Define the p-reductivity dimension
 $\mathrm {rd}_p(\Gamma )$
of
$\mathrm {rd}_p(\Gamma )$
of
 $\Gamma $
to be the minimal n such that there exist a connected n-dimensional reductive algebraic group
$\Gamma $
to be the minimal n such that there exist a connected n-dimensional reductive algebraic group
 $\mathbf {G}$
and an embedding
$\mathbf {G}$
and an embedding
 $\Gamma \hookrightarrow \mathbf {G}(\mathbb {F}_p)$
.
$\Gamma \hookrightarrow \mathbf {G}(\mathbb {F}_p)$
. -
2. Define the reduced p-reductivity dimension
 $\overline {\mathrm {rd}}_p(\Gamma )$
by where
$\overline {\mathrm {rd}}_p(\Gamma )$
by where $$ \begin{align*}\overline{\mathrm{rd}}_p(\Gamma):=\mathrm{rd}_p(\Gamma/\operatorname{\mathrm{Rad}}_p(\Gamma)),\end{align*} $$
$$ \begin{align*}\overline{\mathrm{rd}}_p(\Gamma):=\mathrm{rd}_p(\Gamma/\operatorname{\mathrm{Rad}}_p(\Gamma)),\end{align*} $$
 $\operatorname {\mathrm {Rad}}_p(\Gamma )$
is the maximal normal p-subgroup of
$\operatorname {\mathrm {Rad}}_p(\Gamma )$
is the maximal normal p-subgroup of
 $\Gamma .$
$\Gamma .$
Definition 2.2.2. Let
![]() $(\Gamma ,\theta )$
be a finite symmetric pair and let p be a prime.
$(\Gamma ,\theta )$
be a finite symmetric pair and let p be a prime.
-
1. Define the p-reductivity dimension
 $\mathrm {rd}_p(\Gamma ,\theta )$
of
$\mathrm {rd}_p(\Gamma ,\theta )$
of
 $(\Gamma ,\theta )$
to be the minimal n such that there exist an n-dimensional reductive algebraic group
$(\Gamma ,\theta )$
to be the minimal n such that there exist an n-dimensional reductive algebraic group
 $\mathbf {G}$
, an involution t of
$\mathbf {G}$
, an involution t of
 $\mathbf {G}$
and an embedding
$\mathbf {G}$
and an embedding
 $i:\Gamma \to \mathbf {G}(\mathbb {F}_p)$
such that
$i:\Gamma \to \mathbf {G}(\mathbb {F}_p)$
such that
 $i(\theta (\gamma ))=t(i(\gamma ))$
for all
$i(\theta (\gamma ))=t(i(\gamma ))$
for all
 $\gamma \in \Gamma $
.
$\gamma \in \Gamma $
. -
2. Define the reduced p-reductivity dimension
 $\overline {\mathrm {rd}}_p(\Gamma ,\theta )$
by where
$\overline {\mathrm {rd}}_p(\Gamma ,\theta )$
by where $$ \begin{align*}\overline{\mathrm{rd}}_p(\Gamma,\theta):=\mathrm{rd}_p(\Gamma/\operatorname{\mathrm{Rad}}_p(\Gamma),\bar \theta),\end{align*} $$
$$ \begin{align*}\overline{\mathrm{rd}}_p(\Gamma,\theta):=\mathrm{rd}_p(\Gamma/\operatorname{\mathrm{Rad}}_p(\Gamma),\bar \theta),\end{align*} $$
 $\bar \theta $
is the involution of
$\bar \theta $
is the involution of
 $\Gamma /\operatorname {\mathrm {Rad}}_p(\Gamma )$
induced by
$\Gamma /\operatorname {\mathrm {Rad}}_p(\Gamma )$
induced by
 $\theta $
.
$\theta $
.
Lemma 2.2.3. For any symmetric pair
![]() $(\Gamma ,\theta )$
and every p,
$(\Gamma ,\theta )$
and every p,
![]() $\mathrm {rd}_p(\Gamma ,\theta )\leq 2 \mathrm {rd}_p(\Gamma )$
.
$\mathrm {rd}_p(\Gamma ,\theta )\leq 2 \mathrm {rd}_p(\Gamma )$
.
Proof. Let
![]() $i:\Gamma \hookrightarrow \mathbf {G}(\mathbb {F}_p)$
with
$i:\Gamma \hookrightarrow \mathbf {G}(\mathbb {F}_p)$
with
![]() $\mathbf {G}$
reductive and
$\mathbf {G}$
reductive and
![]() ${\operatorname {dim}} \, \mathbf {G}=\mathrm {rd}_p(\Gamma )$
. Let
${\operatorname {dim}} \, \mathbf {G}=\mathrm {rd}_p(\Gamma )$
. Let
![]() $\mathbf {H}=\mathbf {G} \times \mathbf {G}$
, let
$\mathbf {H}=\mathbf {G} \times \mathbf {G}$
, let
![]() $t:\mathbf {H} \rightarrow \mathbf {H}$
be the flip
$t:\mathbf {H} \rightarrow \mathbf {H}$
be the flip
![]() $\theta (x,y)=(y,x)$
and let
$\theta (x,y)=(y,x)$
and let
![]() $j:\Gamma \hookrightarrow \mathbf {H}(\mathbb {F}_p)$
be
$j:\Gamma \hookrightarrow \mathbf {H}(\mathbb {F}_p)$
be
![]() $j(\gamma ) =(i(\gamma ),i(\theta (\gamma )))$
. The triple
$j(\gamma ) =(i(\gamma ),i(\theta (\gamma )))$
. The triple
![]() $(\mathbf {H},t,j)$
gives an equivariant embedding as required.
$(\mathbf {H},t,j)$
gives an equivariant embedding as required.
Next, we introduce some notations relating to multiplicities.
Notation 2.2.4. Let
![]() $\Gamma $
be a finite group.
$\Gamma $
be a finite group.
-
• We denote the set of (isomorphism classes of) complex irreducible representations of
 $\Gamma $
by
$\Gamma $
by
 $\operatorname {Irr} (\Gamma )$
.
$\operatorname {Irr} (\Gamma )$
. -
• We denote the set of (one dimensional) characters of
 $\Gamma $
by
$\Gamma $
by
 $\widehat {\Gamma }$
.
$\widehat {\Gamma }$
. -
• Suppose that
 $\theta $
is an involution of
$\theta $
is an involution of
 $\Gamma $
. Denote
$\Gamma $
. Denote  $$ \begin{align*}\nu(\Gamma,\theta)=\max_{\rho\in \operatorname{Irr}(\Gamma)} {\operatorname{dim}} \rho^{\Gamma^\theta},\end{align*} $$
$$ \begin{align*}\nu(\Gamma,\theta)=\max_{\rho\in \operatorname{Irr}(\Gamma)} {\operatorname{dim}} \rho^{\Gamma^\theta},\end{align*} $$
 $$ \begin{align*}\nu(\Gamma)=\max_{\theta\ \text{involution of}\ \Gamma} \nu(\Gamma,\theta),\end{align*} $$
$$ \begin{align*}\nu(\Gamma)=\max_{\theta\ \text{involution of}\ \Gamma} \nu(\Gamma,\theta),\end{align*} $$
 $$ \begin{align*}\nu^{\prime}_p(\Gamma)=\max_{\theta\ \text{involution of}\ \Gamma}\max_{\substack{\rho\in \operatorname{Irr}(\Gamma) \text{ such that}\\ \rho|_{\operatorname{\mathrm{Rad}}_p(\Gamma)}\ \text{is isotypic}}} {\operatorname{dim}} \rho^{\Gamma^\theta},\end{align*} $$
and
$$ \begin{align*}\nu^{\prime}_p(\Gamma)=\max_{\theta\ \text{involution of}\ \Gamma}\max_{\substack{\rho\in \operatorname{Irr}(\Gamma) \text{ such that}\\ \rho|_{\operatorname{\mathrm{Rad}}_p(\Gamma)}\ \text{is isotypic}}} {\operatorname{dim}} \rho^{\Gamma^\theta},\end{align*} $$
and $$ \begin{align*}\mu(\Gamma,\theta)=\max_{\rho\in \operatorname{Irr}(\Gamma),\,\, \chi \in \widehat{\Gamma^\theta}} {\operatorname{dim}} \rho^{\Gamma^\theta,\chi},\end{align*} $$
$$ \begin{align*}\mu(\Gamma,\theta)=\max_{\rho\in \operatorname{Irr}(\Gamma),\,\, \chi \in \widehat{\Gamma^\theta}} {\operatorname{dim}} \rho^{\Gamma^\theta,\chi},\end{align*} $$
 $$ \begin{align*}\mu(\Gamma)=\max_{\theta\ \text{involution of}\ \Gamma} \mu(\Gamma,\theta).\end{align*} $$
$$ \begin{align*}\mu(\Gamma)=\max_{\theta\ \text{involution of}\ \Gamma} \mu(\Gamma,\theta).\end{align*} $$
2.3 Reformulation of the main theorem
Using the notations above, Theorem A has the following reformulation:
Theorem 2.3.1 (main).
There is an increasing function
![]() $C:\mathbb N\to \mathbb N$
such that, for every prime
$C:\mathbb N\to \mathbb N$
such that, for every prime
![]() $p>2$
and every finite group
$p>2$
and every finite group
![]() $\Gamma $
,
$\Gamma $
,
This theorem appears to be slightly weaker then Theorem A. We will deduce Theorem A from it in §10.1.
3 Preliminaries on finite groups and algebraic groups
In this section, we collect several properties of finite and algebraic groups.
3.1 Finite groups of Lie type
The following theorem is well known:
Theorem 3.1.1. For any finite field F which is not one of
![]() $\mathbb {F}_2,\mathbb {F}_3,\mathbb {F}_4,\mathbb {F}_8,\mathbb {F}_9$
and for any connected, simply-connected, semi-simple algebraic group
$\mathbb {F}_2,\mathbb {F}_3,\mathbb {F}_4,\mathbb {F}_8,\mathbb {F}_9$
and for any connected, simply-connected, semi-simple algebraic group
![]() $\mathbf {G}$
defined over F, the following hold:
$\mathbf {G}$
defined over F, the following hold:
-
1.
 $\mathbf {G}(F)$
is generated by its unipotents.
$\mathbf {G}(F)$
is generated by its unipotents. -
2.
 $H^2(\mathbf {G}( F),A)=1$
, for every trivial
$H^2(\mathbf {G}( F),A)=1$
, for every trivial
 $\mathbf {G}(F)$
-module A.
$\mathbf {G}(F)$
-module A. -
3.
 $\mathbf {G}(F)$
is perfect.
$\mathbf {G}(F)$
is perfect. -
4.
 $Z(\mathbf {G} (F))=Z(\mathbf {G})(F)$
.
$Z(\mathbf {G} (F))=Z(\mathbf {G})(F)$
. -
5.
 $|Z(\mathbf {G}( F))|\leq 2^{{\operatorname {dim}} \mathbf {G}}$
.
$|Z(\mathbf {G}( F))|\leq 2^{{\operatorname {dim}} \mathbf {G}}$
.
Remark 3.1.2. Claim (1) follows from [Reference SteinbergSte68, Theorem 12.4], so Claim (2) follows from [Reference SteinbergSte68, Remark 12.8(b)].
Claims (3) and (4) follow from Claim (1) and [Reference MargulisMar91, Theorem 1.5.6].
By Claim (4),
![]() $|Z(\mathbf {G}(F))| \leq |Z(\mathbf {G}(\overline {F}))|$
. Since both functions
$|Z(\mathbf {G}(F))| \leq |Z(\mathbf {G}(\overline {F}))|$
. Since both functions
![]() $\mathbf {G} \mapsto |Z(\mathbf {G}(\overline {F}))|$
and
$\mathbf {G} \mapsto |Z(\mathbf {G}(\overline {F}))|$
and
![]() $\mathbf {G} \mapsto 2^{{\operatorname {dim}} \mathbf {G}}$
are multiplicative, it is enough to prove Claim (5) in the case
$\mathbf {G} \mapsto 2^{{\operatorname {dim}} \mathbf {G}}$
are multiplicative, it is enough to prove Claim (5) in the case
![]() $\mathbf {G}$
is simple. For the classical groups, this is a simple inspection; for the exceptional groups, use the fact that the size of the center is equal to the determinant of the Cartan matrix of the Dynkin diagram of
$\mathbf {G}$
is simple. For the classical groups, this is a simple inspection; for the exceptional groups, use the fact that the size of the center is equal to the determinant of the Cartan matrix of the Dynkin diagram of
![]() $\mathbf {G}$
.
$\mathbf {G}$
.
Corollary 3.1.3. Let F be a finite field of characteristic greater than
![]() $3$
, let
$3$
, let
![]() $\mathbf {G}$
be a connected reductive group over F and let
$\mathbf {G}$
be a connected reductive group over F and let
![]() $\phi :\widetilde {\mathbf {G} '} \rightarrow \mathbf {G}'$
be the universal cover of the derived subgroup
$\phi :\widetilde {\mathbf {G} '} \rightarrow \mathbf {G}'$
be the universal cover of the derived subgroup
![]() $\mathbf {G}'$
. Then
$\mathbf {G}'$
. Then
![]() $\phi \left( \widetilde {\mathbf {G}'} (F)\right) = \mathbf {G}(F)'$
.
$\phi \left( \widetilde {\mathbf {G}'} (F)\right) = \mathbf {G}(F)'$
.
Proof. The inclusion
![]() $\phi \left( \widetilde {\mathbf {G}'} (F)\right) \subseteq \mathbf {G}(F)'$
follows from 3.1.1(3). For the other direction, it is enough to show that a commutator of two elements of
$\phi \left( \widetilde {\mathbf {G}'} (F)\right) \subseteq \mathbf {G}(F)'$
follows from 3.1.1(3). For the other direction, it is enough to show that a commutator of two elements of
![]() $\mathbf {G}(F)$
belongs to
$\mathbf {G}(F)$
belongs to
![]() $\phi \left( \widetilde {\mathbf {G}'} (F)\right)$
. Let
$\phi \left( \widetilde {\mathbf {G}'} (F)\right)$
. Let
![]() $g_1,g_2\in \mathbf {G}(F)$
. Choose
$g_1,g_2\in \mathbf {G}(F)$
. Choose
![]() $z_1,z_2\in Z\left( \mathbf {G}(\overline {F})\right)$
such that
$z_1,z_2\in Z\left( \mathbf {G}(\overline {F})\right)$
such that
![]() $g_1z_1,g_2z_2\in \mathbf {G}'(\overline {F})$
, and choose elements
$g_1z_1,g_2z_2\in \mathbf {G}'(\overline {F})$
, and choose elements
![]() $h_1,h_2\in \widetilde {\mathbf {G}'}(\overline {F})$
such that
$h_1,h_2\in \widetilde {\mathbf {G}'}(\overline {F})$
such that
![]() $\phi (h_1)=g_1z_1,\phi (h_2)=g_2z_2$
. Since
$\phi (h_1)=g_1z_1,\phi (h_2)=g_2z_2$
. Since
![]() $\phi ^{-1} (Z(\mathbf {G}'))=Z \left( \widetilde {\mathbf {G}'} \right)$
, the element
$\phi ^{-1} (Z(\mathbf {G}'))=Z \left( \widetilde {\mathbf {G}'} \right)$
, the element
![]() $[h_1,h_2]\in \widetilde {\mathbf {G}'}(\overline {F})$
is independent of the choices of
$[h_1,h_2]\in \widetilde {\mathbf {G}'}(\overline {F})$
is independent of the choices of
![]() $z_i$
and
$z_i$
and
![]() $h_i$
and hence is fixed by
$h_i$
and hence is fixed by
![]() $\operatorname {\mathrm {Gal}}(\overline {F}/F)$
. Therefore,
$\operatorname {\mathrm {Gal}}(\overline {F}/F)$
. Therefore,
![]() $[h_1,h_2]\in \widetilde {\mathbf {G}'}(F)$
. Hence,
$[h_1,h_2]\in \widetilde {\mathbf {G}'}(F)$
. Hence,
![]() $[g_1,g_2]=\phi ([h_1,h_2])\in \phi \left( \widetilde {\mathbf {G}'} (F)\right)$
.
$[g_1,g_2]=\phi ([h_1,h_2])\in \phi \left( \widetilde {\mathbf {G}'} (F)\right)$
.
Corollary 3.1.3 and Theorem 3.1.1(3) imply the following:
Corollary 3.1.4. Let F be a finite field of characteristic greater than
![]() $3$
and let
$3$
and let
![]() $\mathbf {G}$
be a connected reductive group over F. Then
$\mathbf {G}$
be a connected reductive group over F. Then
![]() $\mathbf {G}(F)'$
is perfect.
$\mathbf {G}(F)'$
is perfect.
Lemma 3.1.5. Let
![]() $\phi :\tilde {\mathbf {G}}\to \mathbf {G}$
be an isogeny of algebraic groups defined over a finite field
$\phi :\tilde {\mathbf {G}}\to \mathbf {G}$
be an isogeny of algebraic groups defined over a finite field
![]() $\mathbb {F}_q$
and let
$\mathbb {F}_q$
and let
![]() $\mathbf {K}$
be the kernel of
$\mathbf {K}$
be the kernel of
![]() $\phi $
. Then
$\phi $
. Then
Proof. From the long exact sequence of Galois cohomologies
we get
 $$ \begin{align*} \left[ \mathbf{G}(\mathbb{F}_q) : \phi \left( \widetilde{\mathbf{G}}(\mathbb{F}_q) \right) \right] &= |Ker(H^1(Gal(\overline {\mathbb{F}}_q/\mathbb{F}_q), K(\overline{\mathbb{F}}_q))\to H^1(Gal(\overline {\mathbb{F}}_q/\mathbb{F}_q), \widetilde{\mathbf{G}}(\mathbb{F}_q) ))| \\& \leq |H^1(Gal(\overline {\mathbb{F}}_q/\mathbb{F}_q), K(\overline{\mathbb{F}}_q))| \leq |K(\overline{\mathbb{F}}_q)|.\\[-37pt] \end{align*} $$
$$ \begin{align*} \left[ \mathbf{G}(\mathbb{F}_q) : \phi \left( \widetilde{\mathbf{G}}(\mathbb{F}_q) \right) \right] &= |Ker(H^1(Gal(\overline {\mathbb{F}}_q/\mathbb{F}_q), K(\overline{\mathbb{F}}_q))\to H^1(Gal(\overline {\mathbb{F}}_q/\mathbb{F}_q), \widetilde{\mathbf{G}}(\mathbb{F}_q) ))| \\& \leq |H^1(Gal(\overline {\mathbb{F}}_q/\mathbb{F}_q), K(\overline{\mathbb{F}}_q))| \leq |K(\overline{\mathbb{F}}_q)|.\\[-37pt] \end{align*} $$
Lemma 3.1.6. For every connected reductive group
![]() $\mathbf {G}$
defined over a finite field F of characteristic larger than 3, we have
$\mathbf {G}$
defined over a finite field F of characteristic larger than 3, we have
Proof. We can assume that
![]() $\mathbf {G}$
is semisimple. Let
$\mathbf {G}$
is semisimple. Let
![]() $\phi :\widetilde {\mathbf {G}} \rightarrow \mathbf {G}$
be the universal cover. By Theorem 3.1.1(5) and Lemma 3.1.5,
$\phi :\widetilde {\mathbf {G}} \rightarrow \mathbf {G}$
be the universal cover. By Theorem 3.1.1(5) and Lemma 3.1.5,
![]() $| coker \phi | \leq 2^{{\operatorname {dim}} \mathbf {G}}$
. The result follows from Corollary 3.1.3.
$| coker \phi | \leq 2^{{\operatorname {dim}} \mathbf {G}}$
. The result follows from Corollary 3.1.3.
Lemma 3.1.7. Let
![]() $\Gamma _i$
be simple nonabelian groups and let
$\Gamma _i$
be simple nonabelian groups and let
![]() $\Gamma :=\prod _{i=1}^n \Gamma _i$
. Any normal subgroup
$\Gamma :=\prod _{i=1}^n \Gamma _i$
. Any normal subgroup
![]() $\Delta $
of
$\Delta $
of
![]() $\Gamma $
is of the form
$\Gamma $
is of the form
![]() $\Delta =\prod _{i\in I} \Gamma _i$
for some index set
$\Delta =\prod _{i\in I} \Gamma _i$
for some index set
![]() $I\subset \{1,\dots ,n\}$
. The same holds when
$I\subset \{1,\dots ,n\}$
. The same holds when
![]() $ \Gamma _i$
are simple adjoint algebraic groups and
$ \Gamma _i$
are simple adjoint algebraic groups and
![]() $ \Delta $
is a normal algebraic subgroup of
$ \Delta $
is a normal algebraic subgroup of
![]() $ \Gamma $
.
$ \Gamma $
.
Proof. Assume that
![]() $ \Gamma _i$
are simple nonabelian groups and identify
$ \Gamma _i$
are simple nonabelian groups and identify
![]() $ \Gamma _i$
as a subgroup of
$ \Gamma _i$
as a subgroup of
![]() $ \Gamma $
. Let
$ \Gamma $
. Let
![]() $\pi _i: \Gamma \rightarrow \Gamma _i$
be the projection. If
$\pi _i: \Gamma \rightarrow \Gamma _i$
be the projection. If
![]() $ \pi _i( \Delta ) \neq 1$
, then
$ \pi _i( \Delta ) \neq 1$
, then
![]() $[\Delta , \Gamma _i]$
is a nontrivial normal subgroup of
$[\Delta , \Gamma _i]$
is a nontrivial normal subgroup of
![]() $ \Gamma _i$
, so
$ \Gamma _i$
, so
![]() $ \Gamma _i = [ \Delta , \Gamma _i] \subset \Delta $
. Thus, the lemma holds with
$ \Gamma _i = [ \Delta , \Gamma _i] \subset \Delta $
. Thus, the lemma holds with
![]() $I= \left\{ i \mid \pi _i( \Delta ) \neq 1 \right\}$
.
$I= \left\{ i \mid \pi _i( \Delta ) \neq 1 \right\}$
.
The proof in the case where
![]() $ \Gamma _i$
are algebraic is similar.
$ \Gamma _i$
are algebraic is similar.
Corollary 3.1.8. Let
![]() $\Gamma _i$
and
$\Gamma _i$
and
![]() $\Gamma $
be as in Lemma 3.1.7 and let
$\Gamma $
be as in Lemma 3.1.7 and let
![]() $\theta :\Gamma \to \Gamma $
be an automorphism. Then there is a permutation
$\theta :\Gamma \to \Gamma $
be an automorphism. Then there is a permutation
![]() $\sigma \in S_n$
such that
$\sigma \in S_n$
such that
![]() $\theta (\Gamma _i)=\Gamma _{\sigma (i)}$
.
$\theta (\Gamma _i)=\Gamma _{\sigma (i)}$
.
Corollary 3.1.9. If
![]() $p>3$
is a prime number and
$p>3$
is a prime number and
![]() $\mathbf {G}$
is a connected semisimple adjoint group defined over
$\mathbf {G}$
is a connected semisimple adjoint group defined over
![]() $\mathbb {F}_p$
, then any automorphism of
$\mathbb {F}_p$
, then any automorphism of
![]() $\mathbf {G}(\mathbb {F}_p)'$
extends to an algebraic automorphism of
$\mathbf {G}(\mathbb {F}_p)'$
extends to an algebraic automorphism of
![]() $\mathbf {G}$
.
$\mathbf {G}$
.
For the proof, we will need the following:
Theorem 3.1.10 (easy direction of the classification of finite simple groups; cf. [Reference Gorenstein, Lyons and SolomonGLS94, §1] and [Reference SteinbergSte60, 3.2]).
For any two finite fields
![]() $F_1,F_2$
of characteristic greater than 3 and any two absolutely simple and adjoint algebraic groups
$F_1,F_2$
of characteristic greater than 3 and any two absolutely simple and adjoint algebraic groups
![]() $\mathbf {G},\mathbf {H}$
defined over
$\mathbf {G},\mathbf {H}$
defined over
![]() $F_1,F_2$
respectively,
$F_1,F_2$
respectively,
-
1.
 $\mathbf {G}(F_1)'$
is simple.
$\mathbf {G}(F_1)'$
is simple. -
2. If
 $\mathbf {G}(F_1)'\simeq \mathbf {H}(F_2)'$
, then
$\mathbf {G}(F_1)'\simeq \mathbf {H}(F_2)'$
, then
 $F_1\simeq F_2$
and
$F_1\simeq F_2$
and
 $\mathbf {G}\simeq \mathbf {H}$
.
$\mathbf {G}\simeq \mathbf {H}$
. -
3. Any isomorphism
 $\mathbf {G}(F_1)'\to \mathbf {H}(F_2)'$
is the composition of
$\mathbf {G}(F_1)'\to \mathbf {H}(F_2)'$
is the composition of
 $\phi :\mathbf {G}(F_1)' \rightarrow \mathbf {G}^\phi (F_2)'$
and
$\phi :\mathbf {G}(F_1)' \rightarrow \mathbf {G}^\phi (F_2)'$
and
 $\psi : \mathbf {G}^\phi (F_2)' \rightarrow \mathbf {H}(F_2)$
, where
$\psi : \mathbf {G}^\phi (F_2)' \rightarrow \mathbf {H}(F_2)$
, where
 $\phi :F_1 \rightarrow F_2$
is a field isomorphism,
$\phi :F_1 \rightarrow F_2$
is a field isomorphism,
 $\mathbf {G}^\phi =\mathbf {G} \times _{\operatorname {\mathrm {Spec}}(F_1)} \operatorname {\mathrm {Spec}}(F_2)$
and
$\mathbf {G}^\phi =\mathbf {G} \times _{\operatorname {\mathrm {Spec}}(F_1)} \operatorname {\mathrm {Spec}}(F_2)$
and
 $\psi $
is the restriction of an isomorphism
$\psi $
is the restriction of an isomorphism
 $\mathbf {G}^\phi \rightarrow \mathbf {H}$
.
$\mathbf {G}^\phi \rightarrow \mathbf {H}$
.
Proof of Corollary 3.1.9.
Write
![]() $\mathbf {G}=\prod \mathbf {G}_i$
where
$\mathbf {G}=\prod \mathbf {G}_i$
where
![]() $\mathbf {G}_i$
are simple (not necessarily absolutely simple) adjoint groups defined over
$\mathbf {G}_i$
are simple (not necessarily absolutely simple) adjoint groups defined over
![]() $\mathbb {F}_p$
. For each i, there is a finite field
$\mathbb {F}_p$
. For each i, there is a finite field
![]() $\mathbb {F}_{q_i}$
and an absolutely simple adjoint group
$\mathbb {F}_{q_i}$
and an absolutely simple adjoint group
![]() $\mathbf {S}_i$
defined over
$\mathbf {S}_i$
defined over
![]() $\mathbb {F}_{q_i}$
such that
$\mathbb {F}_{q_i}$
such that
![]() $\mathbf {G}_i\cong (\mathbf {S}_i)_{\mathbb {F}_{q_i}/\mathbb {F}_p}$
. We have
$\mathbf {G}_i\cong (\mathbf {S}_i)_{\mathbb {F}_{q_i}/\mathbb {F}_p}$
. We have
![]() $\mathbf {G}(\mathbb {F}_q)'=\prod \mathbf {S}_i(\mathbb {F}_{q_i})'$
. By Theorem 3.1.10(1), the groups
$\mathbf {G}(\mathbb {F}_q)'=\prod \mathbf {S}_i(\mathbb {F}_{q_i})'$
. By Theorem 3.1.10(1), the groups
![]() $\mathbf {S}_i(\mathbb {F}_{q_i})'$
are simple. By Corollary 3.1.8, there is a permutation
$\mathbf {S}_i(\mathbb {F}_{q_i})'$
are simple. By Corollary 3.1.8, there is a permutation
![]() $\sigma $
such that
$\sigma $
such that
![]() $\theta (\mathbf {S}_i(\mathbb {F}_{q_i})')=\mathbf {S}_{\sigma (i)}(\mathbb {F}_{q_\sigma (i)})'$
. The assertion now follows from Theorem 3.1.10(3).
$\theta (\mathbf {S}_i(\mathbb {F}_{q_i})')=\mathbf {S}_{\sigma (i)}(\mathbb {F}_{q_\sigma (i)})'$
. The assertion now follows from Theorem 3.1.10(3).
3.2 A versal family of reductive groups
In order to prove uniform results for all reductive groups of a bounded dimension over an arbitrary finite field, we will use the following lemma.
Lemma 3.2.1. For any integer
![]() $n>0$
, there exist a scheme
$n>0$
, there exist a scheme
![]() ${\mathcal S}_n$
of finite type, a smooth group scheme
${\mathcal S}_n$
of finite type, a smooth group scheme
![]() $\Phi _n:{\mathcal R}_n\to {\mathcal S}_n$
and an involution
$\Phi _n:{\mathcal R}_n\to {\mathcal S}_n$
and an involution
![]() $\tau _n:{\mathcal R}_n\to {\mathcal R}_n$
over
$\tau _n:{\mathcal R}_n\to {\mathcal R}_n$
over
![]() ${\mathcal S}_n$
such that the following hold:
${\mathcal S}_n$
such that the following hold:
-
1. For every finite field F and every
 $s\in \mathcal {S}_n(F)$
, the group
$s\in \mathcal {S}_n(F)$
, the group
 $(\mathcal {R}_n)_s$
is connected and reductive.
$(\mathcal {R}_n)_s$
is connected and reductive. -
2. For every connected and reductive group
 $\mathbf {G}$
of dimension at most n over a finite field F and for any involution t of
$\mathbf {G}$
of dimension at most n over a finite field F and for any involution t of
 $\mathbf {G}$
, there is
$\mathbf {G}$
, there is
 $s \in \mathcal {S}_n(F)$
with
$s \in \mathcal {S}_n(F)$
with  $$ \begin{align*}(\mathbf{G},t)\simeq ((\mathcal{R}_n)_s,(\tau_n)_s).\end{align*} $$
$$ \begin{align*}(\mathbf{G},t)\simeq ((\mathcal{R}_n)_s,(\tau_n)_s).\end{align*} $$
-
3. For any root datum
 ${\mathfrak X}$
, there is a subscheme
${\mathfrak X}$
, there is a subscheme
 ${\mathcal S}^{\mathfrak X}\subset {\mathcal S}_n$
such that, for any geometric point x of
${\mathcal S}^{\mathfrak X}\subset {\mathcal S}_n$
such that, for any geometric point x of
 ${\mathcal S}_n$
, the (absolute) root datum of
${\mathcal S}_n$
, the (absolute) root datum of
 $({\mathcal R}_n)_x$
is
$({\mathcal R}_n)_x$
is
 ${\mathfrak X}$
if and only if x factors through
${\mathfrak X}$
if and only if x factors through
 ${\mathcal S}^{\mathfrak X}$
. Moreover,
${\mathcal S}^{\mathfrak X}$
. Moreover,
 $\mathcal {S} ^{\mathfrak {X}}$
is a union of connected components of
$\mathcal {S} ^{\mathfrak {X}}$
is a union of connected components of
 $\mathcal {S}_n$
.
$\mathcal {S}_n$
.
We prove this lemma in Appendix B. The proof does not work for infinite fields, but we do have the following:
Lemma 3.2.2. There is a function
![]() $C^{lin}:\mathbb {N} \rightarrow \mathbb {N}$
such that any reductive group
$C^{lin}:\mathbb {N} \rightarrow \mathbb {N}$
such that any reductive group
![]() $\mathbf {G}$
over an arbitrary field F has a faithful F-representation of dimension at most
$\mathbf {G}$
over an arbitrary field F has a faithful F-representation of dimension at most
![]() $C^{lin}({\operatorname {dim}}\, \mathbf {G})$
.
$C^{lin}({\operatorname {dim}}\, \mathbf {G})$
.
4 A theorem of Larsen–Pink and its applications
A theorem of Larsen and Pink is central to our proof. In this section, we quote the theorem and extract two corollaries (Corollaries 4.0.13 and 4.1.2) from it.
Definition 4.0.1. Let
![]() $\mathcal {S}$
be a scheme and let
$\mathcal {S}$
be a scheme and let
![]() $f:\mathcal {G} \rightarrow \mathcal {S}$
be a group scheme over
$f:\mathcal {G} \rightarrow \mathcal {S}$
be a group scheme over
![]() $\mathbf {S}$
.
$\mathbf {S}$
.
-
1. A family of subgroups is a pair consisting of a map
 $\pi :\mathcal {T} \rightarrow \mathcal {S}$
and a
$\pi :\mathcal {T} \rightarrow \mathcal {S}$
and a
 $\mathcal {T}$
-subgroup scheme
$\mathcal {T}$
-subgroup scheme
 $\mathcal {H} \subset \mathcal {G} \times _{\mathcal {S}} \mathcal {T}$
. In this case, we write
$\mathcal {H} \subset \mathcal {G} \times _{\mathcal {S}} \mathcal {T}$
. In this case, we write
 $\mathcal {H} \Subset _\pi \mathcal {G}$
.
$\mathcal {H} \Subset _\pi \mathcal {G}$
. -
2. Suppose that
 $\mathcal {H} \Subset _\pi \mathcal {G}$
, that k is a field, that
$\mathcal {H} \Subset _\pi \mathcal {G}$
, that k is a field, that
 $s\in \mathcal {S}(k)$
and that
$s\in \mathcal {S}(k)$
and that
 $\Gamma \subset \mathcal {G}_s(k)$
is a subgroup. We say that
$\Gamma \subset \mathcal {G}_s(k)$
is a subgroup. We say that
 $\Gamma \ k$
-evades
$\Gamma \ k$
-evades
 $\mathcal {H}$
if, for every
$\mathcal {H}$
if, for every
 $t\in \pi ^{-1} (s)(k)$
, we have
$t\in \pi ^{-1} (s)(k)$
, we have
 $\Gamma \not \subset \mathcal {H}_{t}(k)$
.
$\Gamma \not \subset \mathcal {H}_{t}(k)$
.
Definition 4.0.2. Suppose
![]() $\Gamma , \Delta $
are subgroups of some group. We say that
$\Gamma , \Delta $
are subgroups of some group. We say that
![]() $\Gamma $
is big in
$\Gamma $
is big in
![]() $\Delta $
if
$\Delta $
if
![]() $[\Delta ,\Delta ] \subset \Gamma \subset \Delta $
.
$[\Delta ,\Delta ] \subset \Gamma \subset \Delta $
.
The following is a restatement of [Reference Larsen and PinkLP11, Theorem 0.5]:
Theorem 4.0.3. Let
![]() $\mathcal {S}$
be a scheme and let
$\mathcal {S}$
be a scheme and let
![]() $\mathcal {G} \rightarrow \mathcal {S}$
be a group scheme over
$\mathcal {G} \rightarrow \mathcal {S}$
be a group scheme over
![]() $\mathcal {S}$
such that every geometric fiber is connected, simple and adjoint. There is a family of subgroups
$\mathcal {S}$
such that every geometric fiber is connected, simple and adjoint. There is a family of subgroups
![]() $\mathcal {H} \Subset _\pi \mathcal {G}$
such that, for every prime p, every
$\mathcal {H} \Subset _\pi \mathcal {G}$
such that, for every prime p, every
![]() $\overline {\mathbb {F}_p}$
-point
$\overline {\mathbb {F}_p}$
-point
![]() $s:\operatorname {\mathrm {Spec}}(\overline {\mathbb {F}_p}) \rightarrow \mathcal {S}$
, and every
$s:\operatorname {\mathrm {Spec}}(\overline {\mathbb {F}_p}) \rightarrow \mathcal {S}$
, and every
![]() $\Gamma \subset \mathcal {G}_s(\overline {\mathbb {F}_p})$
, if
$\Gamma \subset \mathcal {G}_s(\overline {\mathbb {F}_p})$
, if
![]() $\Gamma \ \overline {\mathbb {F}_p}$
-evades
$\Gamma \ \overline {\mathbb {F}_p}$
-evades
![]() $\mathcal {H}$
, then there is a Frobenius map
$\mathcal {H}$
, then there is a Frobenius map
![]() $\Phi : \mathcal {G}_s \rightarrow \mathcal {G}_s$
such that
$\Phi : \mathcal {G}_s \rightarrow \mathcal {G}_s$
such that
![]() $\Gamma $
is big in
$\Gamma $
is big in
![]() $\mathcal {G}_s(\overline {\mathbb {F}_p})^{\Phi }$
.
$\mathcal {G}_s(\overline {\mathbb {F}_p})^{\Phi }$
.
Recall that, for an algebraic group
![]() $\mathbf {G}$
defined over
$\mathbf {G}$
defined over
![]() $\overline {\mathbb {F}_p}$
, a Frobenius map of
$\overline {\mathbb {F}_p}$
, a Frobenius map of
![]() $\mathbf {G}$
is an automorphism
$\mathbf {G}$
is an automorphism
![]() $\Phi : \mathbf {G} \rightarrow \mathbf {G}$
for which some positive power
$\Phi : \mathbf {G} \rightarrow \mathbf {G}$
for which some positive power
![]() $\Phi ^n$
coincides with some a standard Frobenius.
$\Phi ^n$
coincides with some a standard Frobenius.
Corollary 4.0.4. Let
![]() $\mathcal {S}$
be a scheme and let
$\mathcal {S}$
be a scheme and let
![]() $\mathcal {G} \rightarrow \mathcal {S}$
be a group scheme whose geometric fibers are connected, simple and adjoint. There is a family of subgroups
$\mathcal {G} \rightarrow \mathcal {S}$
be a group scheme whose geometric fibers are connected, simple and adjoint. There is a family of subgroups
![]() $\mathcal {K} \Subset _\tau \mathcal {G}$
such that, for every prime power q, every
$\mathcal {K} \Subset _\tau \mathcal {G}$
such that, for every prime power q, every
![]() $s\in \mathcal {S}(\mathbb {F}_q)$
and every
$s\in \mathcal {S}(\mathbb {F}_q)$
and every
![]() $\Gamma \subset \mathcal {G}_s(\mathbb {F}_q)$
, if
$\Gamma \subset \mathcal {G}_s(\mathbb {F}_q)$
, if
![]() $\Gamma \ \mathbb {F}_q$
-evades
$\Gamma \ \mathbb {F}_q$
-evades
![]() $\mathcal {K}$
, then there is a Frobenius map
$\mathcal {K}$
, then there is a Frobenius map
![]() $\Phi :\mathcal {G}_s(\overline {\mathbb {F}_q}) \rightarrow \mathcal {G}_s(\overline {\mathbb {F}_q})$
such that
$\Phi :\mathcal {G}_s(\overline {\mathbb {F}_q}) \rightarrow \mathcal {G}_s(\overline {\mathbb {F}_q})$
such that
![]() $\Gamma $
is big in
$\Gamma $
is big in
![]() $\mathcal {G}_s(\overline {\mathbb {F}_q})^{\Phi }$
.
$\mathcal {G}_s(\overline {\mathbb {F}_q})^{\Phi }$
.
For the proof of corollary 4.0.4, we use the following preparations:
Definition 4.0.5. Let
![]() ${\mathcal S}$
be a scheme. Fix a closed embedding
${\mathcal S}$
be a scheme. Fix a closed embedding
![]() $(\operatorname {\mathrm {GL}}_n)_{\mathbf {S}} \hookrightarrow \mathbb {A}_{\mathcal {S}}^N$
.
$(\operatorname {\mathrm {GL}}_n)_{\mathbf {S}} \hookrightarrow \mathbb {A}_{\mathcal {S}}^N$
.
-
1. We say that a regular function
 $f: (\operatorname {\mathrm {GL}}_n)_{{\mathcal S}} \rightarrow \mathbb {A}^1$
has degree at most
$f: (\operatorname {\mathrm {GL}}_n)_{{\mathcal S}} \rightarrow \mathbb {A}^1$
has degree at most
 $\delta $
if it is the restriction of a polynomial of degree at most
$\delta $
if it is the restriction of a polynomial of degree at most
 $\delta $
on
$\delta $
on
 $\mathbb {A}^N_{{\mathcal S}}$
.
$\mathbb {A}^N_{{\mathcal S}}$
. -
2. We say that the degree of
 $f: (\operatorname {\mathrm {GL}}_n)_{{\mathcal S}} \rightarrow \mathbb {A}^1$
is
$f: (\operatorname {\mathrm {GL}}_n)_{{\mathcal S}} \rightarrow \mathbb {A}^1$
is
 $\delta $
if its degree is at most
$\delta $
if its degree is at most
 $\delta $
and not at most
$\delta $
and not at most
 $\delta -1$
.
$\delta -1$
. -
3. Define the complexity of an
 $\mathcal {S}$
-subgroup scheme
$\mathcal {S}$
-subgroup scheme
 $\mathcal {L} \subset (\operatorname {\mathrm {GL}}_n)_{{\mathcal S}}$
to be the minimal m such that the polynomials of degree at most m in the ideal
$\mathcal {L} \subset (\operatorname {\mathrm {GL}}_n)_{{\mathcal S}}$
to be the minimal m such that the polynomials of degree at most m in the ideal
 $I(\mathcal {L})$
generate
$I(\mathcal {L})$
generate
 $I(\mathcal {L})$
.
$I(\mathcal {L})$
.
Lemma 4.0.6. For any two integers n and A, there is an integer B such that, for any field F, if
![]() $\mathbf {L} \subset (\operatorname {\mathrm {GL}}_n)_{F}$
is an algebraic subgroup of complexity at most A, then
$\mathbf {L} \subset (\operatorname {\mathrm {GL}}_n)_{F}$
is an algebraic subgroup of complexity at most A, then
![]() $\mathbf {L}^\circ $
is of complexity at most B.
$\mathbf {L}^\circ $
is of complexity at most B.
Proof. For any integer B, the statement ‘the complexity of the connected component of an algebraic group
![]() $\mathbf {L}$
is at most B’ is a first-order statement on the coefficients of the polynomials defining
$\mathbf {L}$
is at most B’ is a first-order statement on the coefficients of the polynomials defining
![]() $\mathbf {L}\subset (GL_n)_{F}$
.
$\mathbf {L}\subset (GL_n)_{F}$
.
The result follows now by ultraproduct argument.
Lemma 4.0.7. Let
![]() ${\mathcal G}\to {\mathcal S}$
be a group scheme and let
${\mathcal G}\to {\mathcal S}$
be a group scheme and let
![]() $\mathcal {H} \Subset _\pi \mathcal {G}$
be a family of subgroups.
$\mathcal {H} \Subset _\pi \mathcal {G}$
be a family of subgroups.
-
1. For any integer
 $d\in \mathbb N$
, there exists a family of subgroups
$d\in \mathbb N$
, there exists a family of subgroups
 $\mathcal {K} \Subset _\tau \mathcal {G}$
such that, for any geometric point s of
$\mathcal {K} \Subset _\tau \mathcal {G}$
such that, for any geometric point s of
 $\mathcal {S}$
and any d geometric points
$\mathcal {S}$
and any d geometric points
 $s_1,\ldots ,s_d$
of
$s_1,\ldots ,s_d$
of
 $\pi ^{-1} (s)$
, the group
$\pi ^{-1} (s)$
, the group
 $\mathcal {H}_{s_1} \cap \cdots \cap \mathcal {H}_{s_d}$
is of the form
$\mathcal {H}_{s_1} \cap \cdots \cap \mathcal {H}_{s_d}$
is of the form
 $\mathcal {K}_t$
, where t is a point over s (i.e.,
$\mathcal {K}_t$
, where t is a point over s (i.e.,
 $\tau (t)=s$
).
$\tau (t)=s$
). -
2. There exists a family of subgroups
 $\mathcal {P} \Subset _\phi \mathcal {G}$
such that, for any geometric point s of
$\mathcal {P} \Subset _\phi \mathcal {G}$
such that, for any geometric point s of
 $\mathcal {S}$
, any open subgroup of
$\mathcal {S}$
, any open subgroup of
 $\mathcal {G}_{s}$
is of the form
$\mathcal {G}_{s}$
is of the form
 $\mathcal {P}_t$
, where t is a point over s.
$\mathcal {P}_t$
, where t is a point over s.
Proof.
-
1. Let
 ${\mathcal S}'$
be the domain of definition of
${\mathcal S}'$
be the domain of definition of
 $\pi $
and let
$\pi $
and let
 ${\mathcal G}_{{\mathcal S}'}:={\mathcal G}\times _{\mathcal S} {\mathcal S}'$
. Define and
${\mathcal G}_{{\mathcal S}'}:={\mathcal G}\times _{\mathcal S} {\mathcal S}'$
. Define and $$ \begin{align*}{\mathcal K}:={\mathcal H} \times_{{\mathcal G}_{{\mathcal S}'}} \cdots \times_{{\mathcal G}_{{\mathcal S}'}}{\mathcal H}\end{align*} $$
to be the d-fold fibered products. The natural maps
$$ \begin{align*}{\mathcal K}:={\mathcal H} \times_{{\mathcal G}_{{\mathcal S}'}} \cdots \times_{{\mathcal G}_{{\mathcal S}'}}{\mathcal H}\end{align*} $$
to be the d-fold fibered products. The natural maps $$ \begin{align*}{\mathcal S}":={\mathcal S}' \times_{{\mathcal S}} \cdots \times_{{\mathcal S}'} {\mathcal S}'\end{align*} $$
$$ \begin{align*}{\mathcal S}":={\mathcal S}' \times_{{\mathcal S}} \cdots \times_{{\mathcal S}'} {\mathcal S}'\end{align*} $$
 $\mathcal {S}" \rightarrow \mathcal {S}$
and
$\mathcal {S}" \rightarrow \mathcal {S}$
and
 ${\mathcal K}\to {\mathcal S}"$
give a subfamily as required.
${\mathcal K}\to {\mathcal S}"$
give a subfamily as required.
-
2. After passing to a stratification of
 $\mathcal {S}$
, we can assume that
$\mathcal {S}$
, we can assume that
 $\mathcal {G} \subset (\operatorname {\mathrm {GL}}_n)_{\mathcal {S}}$
is closed. Fix a closed embedding
$\mathcal {G} \subset (\operatorname {\mathrm {GL}}_n)_{\mathcal {S}}$
is closed. Fix a closed embedding
 $(\operatorname {\mathrm {GL}}_n)_{\mathcal {S}} \hookrightarrow \mathbb {A}_{\mathcal {S}}^N$
.
$(\operatorname {\mathrm {GL}}_n)_{\mathcal {S}} \hookrightarrow \mathbb {A}_{\mathcal {S}}^N$
.Since
 $\mathcal {G} \rightarrow \mathcal {S}$
is of finite type, there is a bound D on the complexity of all subgroups
$\mathcal {G} \rightarrow \mathcal {S}$
is of finite type, there is a bound D on the complexity of all subgroups
 $\mathcal {G}_{s}$
, where s ranges over all geometric points of
$\mathcal {G}_{s}$
, where s ranges over all geometric points of
 $\mathcal {S}$
. By Lemma 4.0.6, there is a bound E on the complexity of all subgroups
$\mathcal {S}$
. By Lemma 4.0.6, there is a bound E on the complexity of all subgroups
 $(\mathcal {G}_{s})^\circ $
, where s ranges over all geometric points of
$(\mathcal {G}_{s})^\circ $
, where s ranges over all geometric points of
 $\mathcal {S}$
. Since
$\mathcal {S}$
. Since
 $\mathcal {G} \rightarrow \mathcal {S}$
is of finite type, there is a constant C such that, for any geometric point s of
$\mathcal {G} \rightarrow \mathcal {S}$
is of finite type, there is a constant C such that, for any geometric point s of
 $\mathcal {S}$
, the group
$\mathcal {S}$
, the group
 $\mathcal {G}_{s}$
has at most C connected components. We get that there is a constant M such that for any geometric point
$\mathcal {G}_{s}$
has at most C connected components. We get that there is a constant M such that for any geometric point
 $s\in {\mathcal S}$
, any open subgroup of
$s\in {\mathcal S}$
, any open subgroup of
 $\mathcal {G}_s$
has complexity at most M.
$\mathcal {G}_s$
has complexity at most M.There is a morphism
 $\mathcal {T} \rightarrow \mathcal {S}$
and a family of subgroups
$\mathcal {T} \rightarrow \mathcal {S}$
and a family of subgroups
 $\mathcal {P} \subset \mathcal {G}_{\mathcal {T}} \rightarrow \mathcal {T}$
such that the following holds: for every prime power q, every
$\mathcal {P} \subset \mathcal {G}_{\mathcal {T}} \rightarrow \mathcal {T}$
such that the following holds: for every prime power q, every
 $s\in \mathcal {S}(\mathbb {F}_q)$
and every algebraic subgroup
$s\in \mathcal {S}(\mathbb {F}_q)$
and every algebraic subgroup
 $\mathcal {P} \subset \mathcal {G}_s$
which is defined over
$\mathcal {P} \subset \mathcal {G}_s$
which is defined over
 $\mathbb {F}_q$
and has complexity at most M, we have that
$\mathbb {F}_q$
and has complexity at most M, we have that
 $\mathcal {P}=\mathcal {P}_t$
, for some
$\mathcal {P}=\mathcal {P}_t$
, for some
 $t\in \mathcal {T}(\mathbb {F}_q)$
. By the arguments above, this family satisfies the requirements.
$t\in \mathcal {T}(\mathbb {F}_q)$
. By the arguments above, this family satisfies the requirements.
Proof of Corollary 4.0.4.
It is enough to construct
![]() $\mathcal {K}$
and prove that the claim holds for all but finitely many primes. Let
$\mathcal {K}$
and prove that the claim holds for all but finitely many primes. Let
![]() $\pi :\mathcal {S}'\rightarrow \mathcal {S}$
and
$\pi :\mathcal {S}'\rightarrow \mathcal {S}$
and
![]() $\mathcal {H} \rightarrow \mathcal {S}'$
be as in Theorem 4.0.3 and let
$\mathcal {H} \rightarrow \mathcal {S}'$
be as in Theorem 4.0.3 and let
![]() $d={\operatorname {dim}}_{\mathcal S}\, \mathcal {G}$
.
$d={\operatorname {dim}}_{\mathcal S}\, \mathcal {G}$
.
By Lemma 4.0.7, we have a family
![]() $\mathcal {K}\Subset _{\tau } \mathcal {G}$
, with
$\mathcal {K}\Subset _{\tau } \mathcal {G}$
, with
![]() $\tau :{\mathcal T}\to {\mathcal S}$
, such that, for any geometric point s of
$\tau :{\mathcal T}\to {\mathcal S}$
, such that, for any geometric point s of
![]() $\mathcal {S}$
and any d geometric points
$\mathcal {S}$
and any d geometric points
![]() $s_1,\ldots ,s_d$
of
$s_1,\ldots ,s_d$
of
![]() $\pi ^{-1} (s)$
, any open subgroup of
$\pi ^{-1} (s)$
, any open subgroup of
![]() $\mathcal {H}_{s_1} \cap \cdots \cap \mathcal {H}_{s_d}$
is of the form
$\mathcal {H}_{s_1} \cap \cdots \cap \mathcal {H}_{s_d}$
is of the form
![]() $\mathcal {K}_t$
, where t is a point over s (i.e.,
$\mathcal {K}_t$
, where t is a point over s (i.e.,
![]() $\tau (t)=s$
). We show that such a family
$\tau (t)=s$
). We show that such a family
![]() $\mathcal {K}$
satisfies the conclusion of the Corollary.
$\mathcal {K}$
satisfies the conclusion of the Corollary.
Let q be a prime power,
![]() $s\in \mathcal {S}(\mathbb {F}_q)$
, and
$s\in \mathcal {S}(\mathbb {F}_q)$
, and
![]() $\Gamma \subset \mathcal {G}_s(\mathbb {F}_q)$
that
$\Gamma \subset \mathcal {G}_s(\mathbb {F}_q)$
that
![]() $\mathbb {F}_q$
-evades
$\mathbb {F}_q$
-evades
![]() $\mathcal {K}$
. Let
$\mathcal {K}$
. Let
![]() $F: \pi ^{-1}(s)\to \pi ^{-1}(s)$
be the geometric Frobenius. We first show that
$F: \pi ^{-1}(s)\to \pi ^{-1}(s)$
be the geometric Frobenius. We first show that
![]() $\Gamma \ \overline {\mathbb {F}_q}$
-evades
$\Gamma \ \overline {\mathbb {F}_q}$
-evades
![]() $\mathcal {H}$
. Assuming the contrary, there is
$\mathcal {H}$
. Assuming the contrary, there is
![]() $s' \in \pi ^{-1} (s)(\overline {\mathbb {F}_q})$
such that
$s' \in \pi ^{-1} (s)(\overline {\mathbb {F}_q})$
such that
![]() $\Gamma \subset \mathcal {H}_{s'}(\overline {\mathbb {F}_q})$
. For every finite subset
$\Gamma \subset \mathcal {H}_{s'}(\overline {\mathbb {F}_q})$
. For every finite subset
![]() $I \subset \mathbb {Z}$
, denote
$I \subset \mathbb {Z}$
, denote
![]() $\mathbf {H}_I=\bigcap _{i \in I} \mathcal {H}_{F^is'}$
. There are
$\mathbf {H}_I=\bigcap _{i \in I} \mathcal {H}_{F^is'}$
. There are
![]() $i_1,\ldots ,i_d$
such that
$i_1,\ldots ,i_d$
such that
![]() ${\operatorname {dim}}\, \mathbf {H}_{\{i_1,\ldots ,i_d\}}=\min \left\{ {\operatorname {dim}}\, \mathbf {H}_I \mid I \subset \mathbb {Z} \text { finite}\right\}$
. The group
${\operatorname {dim}}\, \mathbf {H}_{\{i_1,\ldots ,i_d\}}=\min \left\{ {\operatorname {dim}}\, \mathbf {H}_I \mid I \subset \mathbb {Z} \text { finite}\right\}$
. The group
![]() $\mathbf {H}_{\{i_1,\ldots ,i_d\}}^\circ $
is invariant under the Frobenius, so it is defined over
$\mathbf {H}_{\{i_1,\ldots ,i_d\}}^\circ $
is invariant under the Frobenius, so it is defined over
![]() $\mathbb {F}_q$
. It follows that the group
$\mathbb {F}_q$
. It follows that the group
![]() $\Gamma \mathbf {H}^{\circ }_{\{i_1,\ldots ,i_d\}}$
is also defined over
$\Gamma \mathbf {H}^{\circ }_{\{i_1,\ldots ,i_d\}}$
is also defined over
![]() $\mathbb {F}_q$
. By the assumption on
$\mathbb {F}_q$
. By the assumption on
![]() $\mathcal {K}$
, we have
$\mathcal {K}$
, we have
![]() $\Gamma \mathbf {H}_{\{i_1,\ldots ,i_d\}}^\circ = \mathcal {K}_t$
, for some
$\Gamma \mathbf {H}_{\{i_1,\ldots ,i_d\}}^\circ = \mathcal {K}_t$
, for some
![]() $t\in \mathcal {T}(\mathbb {F}_q)$
. This contradicts the assumption that
$t\in \mathcal {T}(\mathbb {F}_q)$
. This contradicts the assumption that
![]() $\Gamma \ \mathbb {F}_q$
-evades
$\Gamma \ \mathbb {F}_q$
-evades
![]() $\mathcal {K}$
.
$\mathcal {K}$
.
The result now follows from Theorem 4.0.3.
Proposition 4.0.8. There is a function
![]() ${C_{LP0}}:\mathbb {N} \rightarrow \mathbb {N}$
such that, if p is a prime number,
${C_{LP0}}:\mathbb {N} \rightarrow \mathbb {N}$
such that, if p is a prime number,
![]() $\mathbf {G}$
is a connected algebraic group over
$\mathbf {G}$
is a connected algebraic group over
![]() $\mathbb {F}_p$
,
$\mathbb {F}_p$
,
![]() $t:\mathbf {G} \rightarrow \mathbf {G}$
is an involution, and
$t:\mathbf {G} \rightarrow \mathbf {G}$
is an involution, and
![]() $\Gamma \subset \mathbf {G}(\mathbb {F}_p)$
is t-invariant, then there is a normal t-invariant subgroup
$\Gamma \subset \mathbf {G}(\mathbb {F}_p)$
is t-invariant, then there is a normal t-invariant subgroup
![]() $\Delta \triangleleft \Gamma $
of index at most
$\Delta \triangleleft \Gamma $
of index at most
![]() ${C_{LP0}}({\operatorname {dim}}(\mathbf {G}))$
, a connected reductive group
${C_{LP0}}({\operatorname {dim}}(\mathbf {G}))$
, a connected reductive group
![]() $\mathbf {H}$
defined over
$\mathbf {H}$
defined over
![]() $\mathbb {F}_p$
, an involution s of
$\mathbb {F}_p$
, an involution s of
![]() $\mathbf {H}$
and an
$\mathbf {H}$
and an
![]() $S_2$
-equivariant homomorphism
$S_2$
-equivariant homomorphism
![]() $\rho : \Delta \rightarrow \mathbf {H}(\mathbb {F}_p)$
such that:
$\rho : \Delta \rightarrow \mathbf {H}(\mathbb {F}_p)$
such that:
-
1.
 ${\operatorname {dim}} \mathbf {H} \leq {\operatorname {dim}} \mathbf {G}$
.
${\operatorname {dim}} \mathbf {H} \leq {\operatorname {dim}} \mathbf {G}$
. -
2.
 $\ker \rho $
is a p-group.
$\ker \rho $
is a p-group. -
3. If
 ${\operatorname {dim}} \, \mathbf {H} = {\operatorname {dim}} \, \mathbf {G}$
, then
${\operatorname {dim}} \, \mathbf {H} = {\operatorname {dim}} \, \mathbf {G}$
, then
 $\ker \rho =1$
.
$\ker \rho =1$
. -
4.
 $\rho (\Delta )$
is big in
$\rho (\Delta )$
is big in
 $\mathbf {H}(\mathbb {F}_p)$
.
$\mathbf {H}(\mathbb {F}_p)$
.
For the proof, we will need some preparations:
Lemma 4.0.9. Let
![]() $p>3$
, let
$p>3$
, let
![]() $\mathbf {H}$
be a connected semi-simple group over
$\mathbf {H}$
be a connected semi-simple group over
![]() $\mathbb {F}_p$
and let
$\mathbb {F}_p$
and let
![]() $1\to C\to E\to \mathbf {H}(\mathbb {F}_p)' \rightarrow 1$
be a finite central extension. Then there is a finite central extension
$1\to C\to E\to \mathbf {H}(\mathbb {F}_p)' \rightarrow 1$
be a finite central extension. Then there is a finite central extension
![]() $\mathbf {E}$
of
$\mathbf {E}$
of
![]() $\mathbf {H}$
and an embedding
$\mathbf {H}$
and an embedding
![]() $E \hookrightarrow \mathbf {E}(\mathbb {F}_p)$
such that the diagram
$E \hookrightarrow \mathbf {E}(\mathbb {F}_p)$
such that the diagram

commutes. In addition,
-
1. If
 $\sigma $
is an automorphism of
$\sigma $
is an automorphism of
 $\mathbf {H}$
,
$\mathbf {H}$
,
 $\tau $
is an automorphism of E and the map
$\tau $
is an automorphism of E and the map
 $E \rightarrow \mathbf {H}(\mathbb {F}_p)'$
is equivariant, then there is an automorphism of
$E \rightarrow \mathbf {H}(\mathbb {F}_p)'$
is equivariant, then there is an automorphism of
 $\mathbf {E}$
such that the map
$\mathbf {E}$
such that the map
 $\mathbf {E} \rightarrow \mathbf {H}$
is equivariant.
$\mathbf {E} \rightarrow \mathbf {H}$
is equivariant. -
2. If
 $|C|$
is prime to p, then
$|C|$
is prime to p, then
 $E \cap \mathbf {E}^\circ $
is big in
$E \cap \mathbf {E}^\circ $
is big in
 $\mathbf {E}^\circ (\mathbb {F}_p)$
.
$\mathbf {E}^\circ (\mathbb {F}_p)$
.
Proof. Let
![]() $\widetilde {\mathbf {H}}$
be the universal cover of
$\widetilde {\mathbf {H}}$
be the universal cover of
![]() $\mathbf {H}$
. By Theorem 3.1.1, the universal central extension (or universal cover; cf. [Reference MooreMoo68, §1]) of
$\mathbf {H}$
. By Theorem 3.1.1, the universal central extension (or universal cover; cf. [Reference MooreMoo68, §1]) of
![]() $\mathbf {H}(\mathbb {F}_p)'$
is
$\mathbf {H}(\mathbb {F}_p)'$
is
![]() $\widetilde {\mathbf {H}}(\mathbb {F}_p)$
. Denote the kernel of
$\widetilde {\mathbf {H}}(\mathbb {F}_p)$
. Denote the kernel of
![]() $\widetilde {\mathbf {H}}(\mathbb {F}_p) \rightarrow \mathbf {H}(\mathbb {F}_p)' $
by A and note that
$\widetilde {\mathbf {H}}(\mathbb {F}_p) \rightarrow \mathbf {H}(\mathbb {F}_p)' $
by A and note that
The extension
![]() $1 \rightarrow C \rightarrow E \rightarrow \mathbf {H}(\mathbb {F}_p)' \rightarrow 1$
corresponds to a homomorphism
$1 \rightarrow C \rightarrow E \rightarrow \mathbf {H}(\mathbb {F}_p)' \rightarrow 1$
corresponds to a homomorphism
![]() $\alpha :A \rightarrow C$
. In particular,
$\alpha :A \rightarrow C$
. In particular,
![]() $E=\widetilde {\mathbf {H}}(\mathbb {F}_p) \times C / \delta (A)$
, where
$E=\widetilde {\mathbf {H}}(\mathbb {F}_p) \times C / \delta (A)$
, where
![]() $\delta (g)=(\alpha (g),g ^{-1})$
.
$\delta (g)=(\alpha (g),g ^{-1})$
.
Consider A and C as discrete algebraic groups. Let
![]() $\mathbf {C}$
be the zero-dimensional algebraic group
$\mathbf {C}$
be the zero-dimensional algebraic group
and let
The short exact sequence
![]() $1 \rightarrow \mathbf {C} \rightarrow \mathbf {E} \rightarrow \mathbf {H} \rightarrow 1$
is a central extension, the map
$1 \rightarrow \mathbf {C} \rightarrow \mathbf {E} \rightarrow \mathbf {H} \rightarrow 1$
is a central extension, the map
![]() $E = \left( C \times \widetilde {\mathbf {H}}(\mathbb {F}_p)\right) / \delta (A) \rightarrow \mathbf {E}(\mathbb {F}_p)$
is injective and the diagram (1) commutes.
$E = \left( C \times \widetilde {\mathbf {H}}(\mathbb {F}_p)\right) / \delta (A) \rightarrow \mathbf {E}(\mathbb {F}_p)$
is injective and the diagram (1) commutes.
It remains to prove the additional claims. Claim (1) follows from the construction. For Claim (2), assume that
![]() $|C|$
is prime to p. By the construction,
$|C|$
is prime to p. By the construction,
![]() $\mathbf {E}^\circ =\widetilde {\mathbf {H}}/\ker (\alpha )$
. It follows that
$\mathbf {E}^\circ =\widetilde {\mathbf {H}}/\ker (\alpha )$
. It follows that
![]() $E\cap \mathbf {E}^\circ \supset \widetilde {\mathbf {H}}(\mathbb {F}_p)/\ker (\alpha )$
, so the map
$E\cap \mathbf {E}^\circ \supset \widetilde {\mathbf {H}}(\mathbb {F}_p)/\ker (\alpha )$
, so the map
![]() $E \cap \mathbf {E}^\circ \rightarrow \mathbf {H}(\mathbb {F}_p)'$
is onto. Since the order of
$E \cap \mathbf {E}^\circ \rightarrow \mathbf {H}(\mathbb {F}_p)'$
is onto. Since the order of
![]() $Z(\widetilde {\mathbf {H}})(\overline {\mathbb {F}_p})$
is prime to p, the same is true for the size of
$Z(\widetilde {\mathbf {H}})(\overline {\mathbb {F}_p})$
is prime to p, the same is true for the size of
![]() $\mathbf {C}$
and the size of the kernel of
$\mathbf {C}$
and the size of the kernel of
![]() $E \cap \mathbf {E}^\circ \rightarrow \mathbf {H}(\mathbb {F}_p)'$
. Since the kernel of the surjection
$E \cap \mathbf {E}^\circ \rightarrow \mathbf {H}(\mathbb {F}_p)'$
. Since the kernel of the surjection
![]() $E \cap\ \mathbf {E}^\circ \rightarrow \mathbf {H}(\mathbb {F}_p)'$
is prime to p, we have that the number of p-elements of
$E \cap\ \mathbf {E}^\circ \rightarrow \mathbf {H}(\mathbb {F}_p)'$
is prime to p, we have that the number of p-elements of
![]() $E \cap \mathbf {E}^\circ $
is equal to the number of p-elements of
$E \cap \mathbf {E}^\circ $
is equal to the number of p-elements of
![]() $\mathbf {H}(\mathbb {F}_p)'$
. By the same reasoning applied to the surjection
$\mathbf {H}(\mathbb {F}_p)'$
. By the same reasoning applied to the surjection
![]() $\mathbf {E}^\circ (\mathbb {F}_p) \rightarrow \mathbf {H}(\mathbb {F}_p)'$
, this is also the number of p-elements of
$\mathbf {E}^\circ (\mathbb {F}_p) \rightarrow \mathbf {H}(\mathbb {F}_p)'$
, this is also the number of p-elements of
![]() $\mathbf {E}^\circ (\mathbb {F}_p)$
. Hence, all p-elements in
$\mathbf {E}^\circ (\mathbb {F}_p)$
. Hence, all p-elements in
![]() $\mathbf {E}^\circ (\mathbb {F}_p)$
are already in
$\mathbf {E}^\circ (\mathbb {F}_p)$
are already in
![]() $E\cap \mathbf {E}^\circ $
. By Theorem 3.1.1 and Corollary 3.1.3,
$E\cap \mathbf {E}^\circ $
. By Theorem 3.1.1 and Corollary 3.1.3,
![]() $\mathbf {E}^\circ (\mathbb {F}_p)'$
is generated by its p-elements, and the second claim follows.
$\mathbf {E}^\circ (\mathbb {F}_p)'$
is generated by its p-elements, and the second claim follows.
The next lemma follows from [Reference MargulisMar91, Proposition 1.5.5, Theorem 1.5.6 (i)] and Theorem 3.1.1(1).
Lemma 4.0.10. Let
![]() $p>3$
and let
$p>3$
and let
![]() $\mathbf {H}$
be a reductive group over
$\mathbf {H}$
be a reductive group over
![]() $\mathbb {F}_p$
. Then any
$\mathbb {F}_p$
. Then any
![]() $g\in \mathbf {H}(\mathbb {F}_p)$
that commutes with
$g\in \mathbf {H}(\mathbb {F}_p)$
that commutes with
![]() $\mathbf {H}(\mathbb {F}_p)'$
is central in
$\mathbf {H}(\mathbb {F}_p)'$
is central in
![]() $\mathbf {H}$
.
$\mathbf {H}$
.
Proof of Proposition 4.0.8.
For every n, let
![]() $(\mathcal {R}_n,\mathcal {S}_n,\tau _n)$
be the versal family of reductive groups with involutions from Lemma 3.2.1. By Lemma 3.2.1(3), there is a subscheme
$(\mathcal {R}_n,\mathcal {S}_n,\tau _n)$
be the versal family of reductive groups with involutions from Lemma 3.2.1. By Lemma 3.2.1(3), there is a subscheme
![]() $\mathcal {S}^s_n\subset \mathcal {S}_n$
such that, for any geometric point x of
$\mathcal {S}^s_n\subset \mathcal {S}_n$
such that, for any geometric point x of
![]() $\mathcal {S}_n$
, the group
$\mathcal {S}_n$
, the group
![]() $({\mathcal R}_n)_x$
is absolutely simple adjoint iff x factors through
$({\mathcal R}_n)_x$
is absolutely simple adjoint iff x factors through
![]() $\mathcal {S}^s_n$
. Let
$\mathcal {S}^s_n$
. Let
![]() $\mathcal {R}_n^s \subset \mathcal {R}_n$
be the preimage of
$\mathcal {R}_n^s \subset \mathcal {R}_n$
be the preimage of
![]() $\mathcal {S}^s_n$
.
$\mathcal {S}^s_n$
.
Applying Corollary 4.0.4 to
![]() $\mathcal {R}^{s}_n \rightarrow \mathcal {S}^{s}_n$
, we get a family of subgroups
$\mathcal {R}^{s}_n \rightarrow \mathcal {S}^{s}_n$
, we get a family of subgroups
![]() $\mathcal {K}_n \Subset \mathcal {R}^{s}_n$
parameterized by an
$\mathcal {K}_n \Subset \mathcal {R}^{s}_n$
parameterized by an
![]() $\mathcal {S}^{s}_n$
-scheme
$\mathcal {S}^{s}_n$
-scheme
![]() $f:\mathcal {S}_n' \rightarrow \mathcal {S}^{s}_n$
. Let
$f:\mathcal {S}_n' \rightarrow \mathcal {S}^{s}_n$
. Let
![]() $D(n)$
be the maximum of the number of connected components of a group of the form
$D(n)$
be the maximum of the number of connected components of a group of the form
![]() $(\mathcal {K}_n)_x \cap (\tau _n)_{f(x)}(\mathcal {K}_n)_x$
, or of the form
$(\mathcal {K}_n)_x \cap (\tau _n)_{f(x)}(\mathcal {K}_n)_x$
, or of the form
![]() $(\mathcal {K}_n)_x$
, where x is a geometric point of
$(\mathcal {K}_n)_x$
, where x is a geometric point of
![]() $\mathcal {S}_n'$
.
$\mathcal {S}_n'$
.
We define three functions
![]() ${C_{LP0}},{C_{LP0}^{ss}},{C_{LP0}^{adj}}:\mathbb {N} \rightarrow \mathbb {N}$
by recursion. Set
${C_{LP0}},{C_{LP0}^{ss}},{C_{LP0}^{adj}}:\mathbb {N} \rightarrow \mathbb {N}$
by recursion. Set
and, for
![]() $n \geq 2$
, set
$n \geq 2$
, set
Note that
![]() ${C_{LP0}^{adj}} \leq {C_{LP0}^{ss}} \leq {C_{LP0}}$
. We will show that the proposition holds with this choice of
${C_{LP0}^{adj}} \leq {C_{LP0}^{ss}} \leq {C_{LP0}}$
. We will show that the proposition holds with this choice of
![]() ${C_{LP0}}$
. The proof is by induction on
${C_{LP0}}$
. The proof is by induction on
![]() $n:={\operatorname {dim}}\,\mathbf {G}$
. The base of the induction,
$n:={\operatorname {dim}}\,\mathbf {G}$
. The base of the induction,
![]() $n=0$
, is trivial. The induction step is divided to the following steps:
$n=0$
, is trivial. The induction step is divided to the following steps:
-
Step 1: The claim holds if
 $p \leq 3^{n}+1$
with the bound
$p \leq 3^{n}+1$
with the bound
 ${C_{LP0}}$
replaced by
${C_{LP0}}$
replaced by
 ${C_{LP0}^{adj}}$
.
${C_{LP0}^{adj}}$
.In this case, we can take
 $\Delta =1$
, using the bound
$\Delta =1$
, using the bound
 $|\mathbf {G}(\mathbb {F}_p)| \leq (p+1)^{{\operatorname {dim}}\, \mathbf {G}}$
from [Reference NoriNor87, Lemma 3.5].
$|\mathbf {G}(\mathbb {F}_p)| \leq (p+1)^{{\operatorname {dim}}\, \mathbf {G}}$
from [Reference NoriNor87, Lemma 3.5]. -
Step 2: The claim holds if
 $\mathbf {G}$
is semisimple and adjoint, with the following improvements:
$\mathbf {G}$
is semisimple and adjoint, with the following improvements:-
(a) The bound
 ${C_{LP0}}$
is replaced by
${C_{LP0}}$
is replaced by
 ${C_{LP0}^{adj}}$
.
${C_{LP0}^{adj}}$
. -
(b) Either
 $\mathbf {H}$
is semisimple and
$\mathbf {H}$
is semisimple and
 $Ker(\rho )=1$
, or there is a proper connected t-invariant subgroup
$Ker(\rho )=1$
, or there is a proper connected t-invariant subgroup
 $\mathbf {N}<\mathbf {G}$
such that
$\mathbf {N}<\mathbf {G}$
such that
 $[\Gamma :\Gamma \cap \mathbf {N}(\mathbb {F}_p)]<D(n)$
.
$[\Gamma :\Gamma \cap \mathbf {N}(\mathbb {F}_p)]<D(n)$
.
By Step 1, we can assume
 $p>3^{n}+1$
. We have
$p>3^{n}+1$
. We have
 $\mathbf {G}=\mathbf {G}_1 \times \cdots \times \mathbf {G}_m$
, where
$\mathbf {G}=\mathbf {G}_1 \times \cdots \times \mathbf {G}_m$
, where
 $\mathbf {G}_i$
are simple and adjoint. We denote the projection
$\mathbf {G}_i$
are simple and adjoint. We denote the projection
 $\mathbf {G} \rightarrow \mathbf {G}_i$
by
$\mathbf {G} \rightarrow \mathbf {G}_i$
by
 $pr_i$
. Each
$pr_i$
. Each
 $\mathbf {G}_i$
is a restriction of scalars from an absolutely simple (and adjoint) group:
$\mathbf {G}_i$
is a restriction of scalars from an absolutely simple (and adjoint) group:
 $\mathbf {G}_i=\operatorname {\mathrm {Res}}_{\mathbb {F}_{q_i}/\mathbb {F}_p} \mathbf {S}_i$
.
$\mathbf {G}_i=\operatorname {\mathrm {Res}}_{\mathbb {F}_{q_i}/\mathbb {F}_p} \mathbf {S}_i$
.For any
 $i\in \{1,\dots , m\}$
, we will define a point
$i\in \{1,\dots , m\}$
, we will define a point
 $\sigma _i\in \mathcal {S}^s_n(\mathbb {F}_{q_i})$
. By Corollary 3.1.8, for any i, we have
$\sigma _i\in \mathcal {S}^s_n(\mathbb {F}_{q_i})$
. By Corollary 3.1.8, for any i, we have
 $t(\mathbf {G}_i)=\mathbf {G}_j$
, for some j. If
$t(\mathbf {G}_i)=\mathbf {G}_j$
, for some j. If
 $i\neq j$
, we take
$i\neq j$
, we take
 $\sigma _i\in \mathcal {S}^s_n(\mathbb {F}_{q_i})$
to be such that
$\sigma _i\in \mathcal {S}^s_n(\mathbb {F}_{q_i})$
to be such that
 $(\mathcal {R}_n)_{\sigma _i}\cong \mathbf {S}_i$
. This is possible since
$(\mathcal {R}_n)_{\sigma _i}\cong \mathbf {S}_i$
. This is possible since
 ${\operatorname {dim}}(\mathbf {S}_i)\leq {\operatorname {dim}}(\mathbf {G}_i)$
. If
${\operatorname {dim}}(\mathbf {S}_i)\leq {\operatorname {dim}}(\mathbf {G}_i)$
. If
 $i= j$
, we take
$i= j$
, we take
 $\sigma _i=\sigma _j\in \mathcal {S}^s_n(\mathbb {F}_{q_i})$
to be such that
$\sigma _i=\sigma _j\in \mathcal {S}^s_n(\mathbb {F}_{q_i})$
to be such that
 $(\mathcal {R}_n)_{\sigma _i}\cong \mathbf {S}_i$
in an
$(\mathcal {R}_n)_{\sigma _i}\cong \mathbf {S}_i$
in an
 $S_2$
-equivariant way.
$S_2$
-equivariant way.In both cases, we identify
 $\mathbf {G}_i(\mathbb {F}_p)$
,
$\mathbf {G}_i(\mathbb {F}_p)$
,
 $\mathbf {S}_i(\mathbb {F}_{q_i})$
, and
$\mathbf {S}_i(\mathbb {F}_{q_i})$
, and
 $(\mathcal {R}_n)_{\sigma _i}(\mathbb {F}_{q_i})$
. Given
$(\mathcal {R}_n)_{\sigma _i}(\mathbb {F}_{q_i})$
. Given
 $\Gamma \subset \mathbf {G}(\mathbb {F}_p)$
, there are two cases:
$\Gamma \subset \mathbf {G}(\mathbb {F}_p)$
, there are two cases:-
Case 1: For some i,
 $pr_i(\Gamma ) \subset \mathbf {G}_i(\mathbb {F}_p)$
does not
$pr_i(\Gamma ) \subset \mathbf {G}_i(\mathbb {F}_p)$
does not
 $\mathbb {F}_{q_i}$
-evade
$\mathbb {F}_{q_i}$
-evade
 $\mathcal {K}_n$
.
$\mathcal {K}_n$
.For simplicity, we assume that
 $t(\mathbf {G}_i)=\mathbf {G}_i$
; if
$t(\mathbf {G}_i)=\mathbf {G}_i$
; if
 $t(\mathbf {G}_i)=\mathbf {G}_j$
, the proof is similar (and simpler). In this case, there is a point
$t(\mathbf {G}_i)=\mathbf {G}_j$
, the proof is similar (and simpler). In this case, there is a point
 $x\in {\mathcal S}'(\mathbb {F}_{q_i})$
that lies over
$x\in {\mathcal S}'(\mathbb {F}_{q_i})$
that lies over
 $\sigma _i$
such that
$\sigma _i$
such that
 $pr_i(\Gamma ) \subset (\mathcal {K}_n)_x(\mathbb {F}_{q_i})$
. Denote
$pr_i(\Gamma ) \subset (\mathcal {K}_n)_x(\mathbb {F}_{q_i})$
. Denote
 $\mathbf K:= \mathcal {K}_x$
. By the definition of
$\mathbf K:= \mathcal {K}_x$
. By the definition of
 $D(n)$
, we have
$D(n)$
, we have
 $|\pi _0(\mathbf K \cap \mathbf t_{\sigma _i}(\mathbf {K}))|\leq D(n)$
. Let
$|\pi _0(\mathbf K \cap \mathbf t_{\sigma _i}(\mathbf {K}))|\leq D(n)$
. Let
 $\mathbf {M}=\operatorname {\mathrm {Res}}_{\mathbb {F}_{q_i}/\mathbb {F}_p}(\mathbf K \cap \mathbf t_{\sigma _i}(\mathbf {K}))$
. We have
$\mathbf {M}=\operatorname {\mathrm {Res}}_{\mathbb {F}_{q_i}/\mathbb {F}_p}(\mathbf K \cap \mathbf t_{\sigma _i}(\mathbf {K}))$
. We have
 $|\pi _0(\mathbf M)|\leq D(n)^n$
.
$|\pi _0(\mathbf M)|\leq D(n)^n$
.Using the identification
 $\mathbf {G}_i=\operatorname {\mathrm {Res}}_{\mathbb {F}_{q_i}/\mathbb {F}_p} \mathbf {S}_i$
, the group
$\mathbf {G}_i=\operatorname {\mathrm {Res}}_{\mathbb {F}_{q_i}/\mathbb {F}_p} \mathbf {S}_i$
, the group
 $\mathbf {M}$
is a subgroup of
$\mathbf {M}$
is a subgroup of
 $\mathbf {G}_i$
and is defined over
$\mathbf {G}_i$
and is defined over
 $\mathbb {F}_p$
. Note that
$\mathbb {F}_p$
. Note that
 $pr_i(\Gamma ) \subset \mathbf {M}(\mathbb {F}_p)$
. Since
$pr_i(\Gamma ) \subset \mathbf {M}(\mathbb {F}_p)$
. Since
 ${\operatorname {dim}}(pr_i ^{-1} (\mathbf {M}))<n$
, the result now follows from the induction step applied to
${\operatorname {dim}}(pr_i ^{-1} (\mathbf {M}))<n$
, the result now follows from the induction step applied to
 $pr_i ^{-1} (\mathbf {M})^\circ $
and
$pr_i ^{-1} (\mathbf {M})^\circ $
and
 $\Gamma \cap pr_i ^{-1} (\mathbf {M})^\circ (\mathbb {F}_p)$
.
$\Gamma \cap pr_i ^{-1} (\mathbf {M})^\circ (\mathbb {F}_p)$
. -
Case 2: For all i,
 $pr_i(\Gamma )\ \mathbb {F}_{q_i}$
-evades
$pr_i(\Gamma )\ \mathbb {F}_{q_i}$
-evades
 $\mathcal {K}_n$
.
$\mathcal {K}_n$
.In this case, there are Frobenius maps
 $\Phi _i: \mathbf {S}_i(\overline {\mathbb {F}_{q_i}}) \rightarrow \mathbf {S}_i(\overline {\mathbb {F}_{q_i}})$
such that
$\Phi _i: \mathbf {S}_i(\overline {\mathbb {F}_{q_i}}) \rightarrow \mathbf {S}_i(\overline {\mathbb {F}_{q_i}})$
such that
 $pr_i(\Gamma )$
is big in
$pr_i(\Gamma )$
is big in
 $\mathbf {S}_i(\overline {\mathbb {F}_{q_i}})^{\Phi _i}$
. Let
$\mathbf {S}_i(\overline {\mathbb {F}_{q_i}})^{\Phi _i}$
. Let
 $\Delta :=\Gamma \cap \prod _i \left( \mathbf {S}_i(\overline {\mathbb {F}_{q_i}})^{\Phi _i} \right) '$
. Since we get
$\Delta :=\Gamma \cap \prod _i \left( \mathbf {S}_i(\overline {\mathbb {F}_{q_i}})^{\Phi _i} \right) '$
. Since we get $$\begin{align*}\left[ \mathbf{S}_i(\overline{\mathbb{F}_{q_i}})^{\Phi_i} : \left( \mathbf{S}_i(\overline{\mathbb{F}_{q_i}})^{\Phi_i} \right) '\right] \leq 2^{{\operatorname{dim}}\, \mathbf{S}_i}, \end{align*}$$
$$\begin{align*}\left[ \mathbf{S}_i(\overline{\mathbb{F}_{q_i}})^{\Phi_i} : \left( \mathbf{S}_i(\overline{\mathbb{F}_{q_i}})^{\Phi_i} \right) '\right] \leq 2^{{\operatorname{dim}}\, \mathbf{S}_i}, \end{align*}$$
 $$\begin{align*}[ \Gamma : \Delta ] \leq 2^{\sum {\operatorname{dim}}\, \mathbf{S}_i} \leq 2^{{\operatorname{dim}}\, \mathbf{G}}\leq {C_{LP0}^{adj}}(n). \end{align*}$$
$$\begin{align*}[ \Gamma : \Delta ] \leq 2^{\sum {\operatorname{dim}}\, \mathbf{S}_i} \leq 2^{{\operatorname{dim}}\, \mathbf{G}}\leq {C_{LP0}^{adj}}(n). \end{align*}$$
Since
 $\Delta \supset \Gamma '$
, it follows that
$\Delta \supset \Gamma '$
, it follows that
 $pr_i(\Delta )=\left( \mathbf {S}_i(\overline {\mathbb {F}_{q_i}})^{\Phi _i} \right) '$
, for all i. Since
$pr_i(\Delta )=\left( \mathbf {S}_i(\overline {\mathbb {F}_{q_i}})^{\Phi _i} \right) '$
, for all i. Since
 $\left( \mathbf {S}_i(\overline {\mathbb {F}_{q_i}})^{\Phi _i}\right)'$
are simple groups, Goursat’s Lemma implies that there is a subset
$\left( \mathbf {S}_i(\overline {\mathbb {F}_{q_i}})^{\Phi _i}\right)'$
are simple groups, Goursat’s Lemma implies that there is a subset
 $I \subset [m]$
such that the projection
$I \subset [m]$
such that the projection
 $\Delta \rightarrow \prod _{i\in I} \left( \mathbf {S}_i(\overline {\mathbb {F}_{q_i}})^{\Phi _i} \right) '$
is an isomorphism. Since
$\Delta \rightarrow \prod _{i\in I} \left( \mathbf {S}_i(\overline {\mathbb {F}_{q_i}})^{\Phi _i} \right) '$
is an isomorphism. Since
 $\Delta $
is perfect and
$\Delta $
is perfect and
 $\Delta \subset \Gamma $
, it follows that
$\Delta \subset \Gamma $
, it follows that
 $\Delta =\Gamma '$
, and, in particular,
$\Delta =\Gamma '$
, and, in particular,
 $t(\Delta )=\Delta $
.
$t(\Delta )=\Delta $
.By [Reference SteinbergSte68, 11.6], there is a connected semisimple
 $\mathbb {F}_p$
group
$\mathbb {F}_p$
group
 $\mathbf {H}$
such that
$\mathbf {H}$
such that
 $\mathbf {H}(\mathbb {F}_p)\cong \prod _{i\in I} \mathbf {S}_i(\overline {\mathbb {F}_{q_i}})^{\Phi _i}$
.
$\mathbf {H}(\mathbb {F}_p)\cong \prod _{i\in I} \mathbf {S}_i(\overline {\mathbb {F}_{q_i}})^{\Phi _i}$
.By Corollary 3.1.9, the restriction of t to
 $\Delta $
extends to an involution s of
$\Delta $
extends to an involution s of
 $\mathbf {H}$
.
$\mathbf {H}$
.By [Reference NoriNor87, Lemma 3.5],
 $(p-1)^{{\operatorname {dim}}\, \mathbf {H}} \leq \left| \mathbf {H}(\mathbb {F}_p) \right|$
and
$(p-1)^{{\operatorname {dim}}\, \mathbf {H}} \leq \left| \mathbf {H}(\mathbb {F}_p) \right|$
and
 $\left| \mathbf {G}(\mathbb {F}_p) \right| \leq (p+1)^{{\operatorname {dim}}\, \mathbf {G}}$
, so Since
$\left| \mathbf {G}(\mathbb {F}_p) \right| \leq (p+1)^{{\operatorname {dim}}\, \mathbf {G}}$
, so Since $$\begin{align*}(p-1)^{{\operatorname{dim}}\, \mathbf{H}} \leq \left| \mathbf{H}(\mathbb{F}_p) \right| \leq | \Delta | 2^{{\operatorname{dim}}\,\mathbf{G}} \leq \left| \mathbf{G}(\mathbb{F}_p) \right|2^{{\operatorname{dim}}\, \mathbf{G}} \leq (2p\kern1.5pt{+}\kern1.5pt2)^{{\operatorname{dim}}\, \mathbf{G}} \leq (3p\kern1.5pt{-}\kern1.5pt3)^{{\operatorname{dim}}\, \mathbf{G}}. \end{align*}$$
$$\begin{align*}(p-1)^{{\operatorname{dim}}\, \mathbf{H}} \leq \left| \mathbf{H}(\mathbb{F}_p) \right| \leq | \Delta | 2^{{\operatorname{dim}}\,\mathbf{G}} \leq \left| \mathbf{G}(\mathbb{F}_p) \right|2^{{\operatorname{dim}}\, \mathbf{G}} \leq (2p\kern1.5pt{+}\kern1.5pt2)^{{\operatorname{dim}}\, \mathbf{G}} \leq (3p\kern1.5pt{-}\kern1.5pt3)^{{\operatorname{dim}}\, \mathbf{G}}. \end{align*}$$
 $p>3^{{\operatorname {dim}}\,\mathbf {G}}+1$
, we have so
$p>3^{{\operatorname {dim}}\,\mathbf {G}}+1$
, we have so $$\begin{align*}\frac{{\operatorname{dim}}\, \mathbf{H}}{{\operatorname{dim}}\,\mathbf{G}} \leq \frac{\log(3p-3)}{\log(p-1)} < 1+\frac{1}{{\operatorname{dim}}\,\mathbf{G}}, \end{align*}$$
$$\begin{align*}\frac{{\operatorname{dim}}\, \mathbf{H}}{{\operatorname{dim}}\,\mathbf{G}} \leq \frac{\log(3p-3)}{\log(p-1)} < 1+\frac{1}{{\operatorname{dim}}\,\mathbf{G}}, \end{align*}$$
 ${\operatorname {dim}}\,\mathbf {H} \leq {\operatorname {dim}}\,\mathbf {G}$
.
${\operatorname {dim}}\,\mathbf {H} \leq {\operatorname {dim}}\,\mathbf {G}$
.
-
-
Step 3: The claim holds if
 $\mathbf {G}$
is semisimple (but not necessarily adjoint), with the bound
$\mathbf {G}$
is semisimple (but not necessarily adjoint), with the bound
 ${C_{LP0}^{ss}}$
.
${C_{LP0}^{ss}}$
.Let
 $\overline {\mathbf {G}}=\mathbf {G}/\mathbf {Z}(\mathbf {G})$
, let
$\overline {\mathbf {G}}=\mathbf {G}/\mathbf {Z}(\mathbf {G})$
, let
 $\pi :\mathbf {G} \rightarrow \overline {\mathbf {G}}$
be the projection and let
$\pi :\mathbf {G} \rightarrow \overline {\mathbf {G}}$
be the projection and let
 $\overline {\Gamma }=\pi (\Gamma )$
. Applying the previous step to
$\overline {\Gamma }=\pi (\Gamma )$
. Applying the previous step to
 $\overline {\Gamma },\overline {\mathbf {G}}$
, there are two possible cases:
$\overline {\Gamma },\overline {\mathbf {G}}$
, there are two possible cases:-
Case 1: There is a proper connected t -invariant subgroup
 $\overline {\mathbf {N}}<\overline {\mathbf {G}}$
such that
$\overline {\mathbf {N}}<\overline {\mathbf {G}}$
such that
 $[\overline \Gamma :\overline \Gamma \cap \overline {\mathbf {N}}(\mathbb {F}_p)]<D(n)$
.
$[\overline \Gamma :\overline \Gamma \cap \overline {\mathbf {N}}(\mathbb {F}_p)]<D(n)$
. -
Case 2: There is a subgroup
 $\overline {\Delta } \subset \overline {\Gamma }$
, a semisimple group
$\overline {\Delta } \subset \overline {\Gamma }$
, a semisimple group
 $\overline {\mathbf {H}}$
with an action of
$\overline {\mathbf {H}}$
with an action of
 $S_2$
and an
$S_2$
and an
 $S_2$
-equivariant injective homomorphism
$S_2$
-equivariant injective homomorphism
 $\overline {\rho }:\overline {\Delta } \rightarrow \overline {\mathbf {H}}(\mathbb {F}_p)$
, such that
$\overline {\rho }:\overline {\Delta } \rightarrow \overline {\mathbf {H}}(\mathbb {F}_p)$
, such that
 $\overline {\rho }(\overline {\Delta })\subset \overline {\mathbf {H}}(\mathbb {F}_p)$
is big and
$\overline {\rho }(\overline {\Delta })\subset \overline {\mathbf {H}}(\mathbb {F}_p)$
is big and
 $[\overline \Gamma :\overline \Delta ]<{C_{LP0}^{adj}}(n)$
.
$[\overline \Gamma :\overline \Delta ]<{C_{LP0}^{adj}}(n)$
.
In the first case, we are done by the induction assumption. For the second case, note that
 $\rho \left( \overline \Delta ' \right)=\overline {\mathbf {H}}(\mathbb {F}_p)'$
and, by Lemma 3.1.6, we have
$\rho \left( \overline \Delta ' \right)=\overline {\mathbf {H}}(\mathbb {F}_p)'$
and, by Lemma 3.1.6, we have
 $[\overline \Delta :\overline \Delta ']\leq 2^n.$
Denote
$[\overline \Delta :\overline \Delta ']\leq 2^n.$
Denote
 $\Delta :=\pi ^{-1}(\overline \Delta ') \cap \Gamma $
. We get that where
$\Delta :=\pi ^{-1}(\overline \Delta ') \cap \Gamma $
. We get that where $$ \begin{align*}[\Gamma:\Delta]<{C_{LP0}^{adj}}(n)2^n={C_{LP0}^{ss}}(n), \end{align*} $$
$$ \begin{align*}[\Gamma:\Delta]<{C_{LP0}^{adj}}(n)2^n={C_{LP0}^{ss}}(n), \end{align*} $$
 $\Delta $
is a central extension of
$\Delta $
is a central extension of
 $\overline {\Delta }'=\overline {\mathbf {H}}(\mathbb {F}_p)'$
. By Lemma 4.0.9, this central extension can be extended to an
$\overline {\Delta }'=\overline {\mathbf {H}}(\mathbb {F}_p)'$
. By Lemma 4.0.9, this central extension can be extended to an
 $S_2$
-equivariant central extension
$S_2$
-equivariant central extension
 $\mathbf {H}$
of
$\mathbf {H}$
of
 $\overline {\mathbf {H}}$
in such a way that the embedding has big image, as required.
$\overline {\mathbf {H}}$
in such a way that the embedding has big image, as required. $$ \begin{align*}\Delta \to \mathbf{H}(\mathbb{F}_p)\end{align*} $$
$$ \begin{align*}\Delta \to \mathbf{H}(\mathbb{F}_p)\end{align*} $$
-
-
Step 4: The claim holds if
 $\mathbf {G}$
is a direct product of a semisimple group and a torus, with the bound
$\mathbf {G}$
is a direct product of a semisimple group and a torus, with the bound
 ${C_{LP0}^{ss}}$
.
${C_{LP0}^{ss}}$
.Write
 $\mathbf {G}=\mathbf {G}'\times \mathbf {T}$
. Let
$\mathbf {G}=\mathbf {G}'\times \mathbf {T}$
. Let
 $p:\mathbf {G}\to \mathbf {G}'$
be the projection and
$p:\mathbf {G}\to \mathbf {G}'$
be the projection and
 $\bar \Gamma :=p(\Gamma )$
. Applying the previous step to
$\bar \Gamma :=p(\Gamma )$
. Applying the previous step to
 $\bar \Gamma $
, we get groups
$\bar \Gamma $
, we get groups
 $\bar \Delta $
and
$\bar \Delta $
and
 $\bar {\mathbf {H}}$
. The claim holds for
$\bar {\mathbf {H}}$
. The claim holds for
 $\Delta :=\bar \Delta \times \mathbf {T}(\mathbb {F}_p)\cap \Gamma $
and
$\Delta :=\bar \Delta \times \mathbf {T}(\mathbb {F}_p)\cap \Gamma $
and
 ${\mathbf {H}}:=\bar {\mathbf {H}}\times \mathbf {T}$
.
${\mathbf {H}}:=\bar {\mathbf {H}}\times \mathbf {T}$
. -
Step 5: The claim holds if
 ${\mathbf {G}}$
is reductive.
${\mathbf {G}}$
is reductive.Let
 $\tilde {\mathbf {G}}:= {\mathbf {G}}' \times Z({\mathbf {G}})^\circ $
. We have an isogeny
$\tilde {\mathbf {G}}:= {\mathbf {G}}' \times Z({\mathbf {G}})^\circ $
. We have an isogeny
 $\pi :\tilde {\mathbf {G}}\to {\mathbf {G}}$
. By Lemma 3.1.5 and Theorem 3.1.1(5),
$\pi :\tilde {\mathbf {G}}\to {\mathbf {G}}$
. By Lemma 3.1.5 and Theorem 3.1.1(5),
 $[{\mathbf {G}}(\mathbb {F}_p), \pi (\tilde {\mathbf {G}}(\mathbb {F}_p))]\leq 2^n$
. Let
$[{\mathbf {G}}(\mathbb {F}_p), \pi (\tilde {\mathbf {G}}(\mathbb {F}_p))]\leq 2^n$
. Let
 $\tilde \Gamma :=\pi ^{-1}(\Gamma )$
. Applying the previous step to
$\tilde \Gamma :=\pi ^{-1}(\Gamma )$
. Applying the previous step to
 $\tilde \Gamma \subset \tilde {\mathbf {G}}(\mathbb {F}_p)$
, we get groups
$\tilde \Gamma \subset \tilde {\mathbf {G}}(\mathbb {F}_p)$
, we get groups
 $\tilde \Delta $
,
$\tilde \Delta $
,
 $\tilde {\mathbf {H}}$
and a map
$\tilde {\mathbf {H}}$
and a map
 $\tilde \rho :\tilde \Delta \to \tilde {\mathbf {H}}(\mathbb {F}_p)$
. Note that
$\tilde \rho :\tilde \Delta \to \tilde {\mathbf {H}}(\mathbb {F}_p)$
. Note that
 $Ker(\pi )\cap \tilde \Delta $
is central in
$Ker(\pi )\cap \tilde \Delta $
is central in
 $\tilde \Delta $
, and thus,
$\tilde \Delta $
, and thus,
 $\tilde \rho (Ker(\pi )\cap \tilde \Delta )$
is central in
$\tilde \rho (Ker(\pi )\cap \tilde \Delta )$
is central in
 $\tilde \rho (\tilde \Delta )$
. Since
$\tilde \rho (\tilde \Delta )$
. Since
 $\rho (\tilde \Delta )$
is big in
$\rho (\tilde \Delta )$
is big in
 $ \tilde {\mathbf {H}}(\mathbb {F}_p)$
, we get (by Lemma 4.0.10) that
$ \tilde {\mathbf {H}}(\mathbb {F}_p)$
, we get (by Lemma 4.0.10) that
 $\tilde \rho (Ker(\pi )\cap \tilde \Delta )$
is central in
$\tilde \rho (Ker(\pi )\cap \tilde \Delta )$
is central in
 $\tilde {\mathbf {H}}$
. Define
$\tilde {\mathbf {H}}$
. Define
 ${\mathbf {H}}=\tilde {\mathbf {H}}/\tilde \rho (Ker(\pi )\cap \tilde \Delta )$
and
${\mathbf {H}}=\tilde {\mathbf {H}}/\tilde \rho (Ker(\pi )\cap \tilde \Delta )$
and
 $\Delta :=\pi (\tilde \Delta )\cong \tilde \Delta /(Ker(\pi )\cap \tilde \Delta )$
. Note that
$\Delta :=\pi (\tilde \Delta )\cong \tilde \Delta /(Ker(\pi )\cap \tilde \Delta )$
. Note that
 $[\Gamma :\Delta ]\leq {C_{LP0}}(n)$
. The map
$[\Gamma :\Delta ]\leq {C_{LP0}}(n)$
. The map
 $\tilde \rho $
desends to a map
$\tilde \rho $
desends to a map
 $\rho :\Delta \to {\mathbf {H}}(\mathbb {F}_p)$
, and we are done.
$\rho :\Delta \to {\mathbf {H}}(\mathbb {F}_p)$
, and we are done. -
Step 6: The claim holds for all connected groups
 ${\mathbf {G}}$
.
${\mathbf {G}}$
.Denoting the unipotent radical of
 ${\mathbf {G}}$
by
${\mathbf {G}}$
by
 $\mathbf {U}$
, t induces an involution on
$\mathbf {U}$
, t induces an involution on
 ${\mathbf {G}} / \mathbf {U}$
, and the projection
${\mathbf {G}} / \mathbf {U}$
, and the projection
 $\pi :{\mathbf {G}} \rightarrow {\mathbf {G}}/\mathbf {U}$
is equivariant. By the previous step, we can assume that
$\pi :{\mathbf {G}} \rightarrow {\mathbf {G}}/\mathbf {U}$
is equivariant. By the previous step, we can assume that
 $\mathbf {U}$
is positive dimensional. Given
$\mathbf {U}$
is positive dimensional. Given
 $\Gamma $
, let
$\Gamma $
, let
 $\bar \Gamma =\pi (\Gamma )$
. By induction, there is a subgroup
$\bar \Gamma =\pi (\Gamma )$
. By induction, there is a subgroup
 $\bar \Delta \subset \bar \Gamma $
, an algebraic group
$\bar \Delta \subset \bar \Gamma $
, an algebraic group
 $\bar {\mathbf {H}}$
and a homomorphism
$\bar {\mathbf {H}}$
and a homomorphism
 $\bar \rho : \bar \Delta \rightarrow {\mathbf {H}} (\mathbb {F}_p)$
. It is easy to see that
$\bar \rho : \bar \Delta \rightarrow {\mathbf {H}} (\mathbb {F}_p)$
. It is easy to see that
 $\Delta := \pi ^{-1} (\bar \Delta )$
,
$\Delta := \pi ^{-1} (\bar \Delta )$
,
 ${\mathbf {H}}:=\bar {\mathbf {H}}$
and
${\mathbf {H}}:=\bar {\mathbf {H}}$
and
 $\rho := \bar \rho \circ \pi $
satisfy the requirements of the proposition.
$\rho := \bar \rho \circ \pi $
satisfy the requirements of the proposition.
Corollary 4.0.11. There is an increasing function
![]() $C_{mon}: \mathbb {N} \rightarrow \mathbb {N}$
for which the following holds. If p is a prime and
$C_{mon}: \mathbb {N} \rightarrow \mathbb {N}$
for which the following holds. If p is a prime and
![]() $\Delta \subset \Gamma $
are finite groups such that
$\Delta \subset \Gamma $
are finite groups such that
![]() $\operatorname {\mathrm {Rad}}_p(\Delta )\neq \Delta \cap \operatorname {\mathrm {Rad}}_p(\Gamma )$
, then there is a normal subgroup
$\operatorname {\mathrm {Rad}}_p(\Delta )\neq \Delta \cap \operatorname {\mathrm {Rad}}_p(\Gamma )$
, then there is a normal subgroup
![]() $\Delta ^\circ \lhd \Delta $
of index at most
$\Delta ^\circ \lhd \Delta $
of index at most
![]() $C_{mon0}(\overline {\mathrm {rd}}_p( \Gamma ))$
satisfying
$C_{mon0}(\overline {\mathrm {rd}}_p( \Gamma ))$
satisfying
![]() $\overline {\mathrm {rd}}_p(\Delta ^\circ ) < \overline {\mathrm {rd}}_p (\Gamma )$
.
$\overline {\mathrm {rd}}_p(\Delta ^\circ ) < \overline {\mathrm {rd}}_p (\Gamma )$
.
For the proof, we will need the following:
Lemma 4.0.12. Let
![]() $p> 3$
be a prime and let
$p> 3$
be a prime and let
![]() ${\mathbf {H}}$
be a reductive group over
${\mathbf {H}}$
be a reductive group over
![]() $\mathbb {F}_p$
. Let
$\mathbb {F}_p$
. Let
![]() $\Gamma <{\mathbf {H}}(\mathbb {F}_p)$
be a big subgroup. Then
$\Gamma <{\mathbf {H}}(\mathbb {F}_p)$
be a big subgroup. Then
![]() $\Gamma $
does not have a nontrivial normal p-subgroup.
$\Gamma $
does not have a nontrivial normal p-subgroup.
Proof. Suppose that P is a nontrivial normal p-subgroup of
![]() $\Gamma $
. Since the index of
$\Gamma $
. Since the index of
![]() ${\mathbf {H}}(\mathbb {F}_p)'$
in
${\mathbf {H}}(\mathbb {F}_p)'$
in
![]() ${\mathbf {H}}(\mathbb {F}_p)$
is prime to p, we have
${\mathbf {H}}(\mathbb {F}_p)$
is prime to p, we have
![]() $P\subset {\mathbf {H}}(\mathbb {F}_p)'$
. For similar reasons,
$P\subset {\mathbf {H}}(\mathbb {F}_p)'$
. For similar reasons,
![]() $P\cap Z({\mathbf {H}}(\mathbb {F}_p)')=1$
. This gives an embedding of P into
$P\cap Z({\mathbf {H}}(\mathbb {F}_p)')=1$
. This gives an embedding of P into
![]() ${\mathbf {H}}(\mathbb {F}_p)'/Z({\mathbf {H}}(\mathbb {F}_p)')$
, which is a product of nonabelian simple groups, a contradiction.
${\mathbf {H}}(\mathbb {F}_p)'/Z({\mathbf {H}}(\mathbb {F}_p)')$
, which is a product of nonabelian simple groups, a contradiction.
Proof of Corollary 4.0.11.
Set
![]() $C_{mon0}(n):=\max (4^n,({C_{LP0}}(n)+1)^n)$
. Suppose that
$C_{mon0}(n):=\max (4^n,({C_{LP0}}(n)+1)^n)$
. Suppose that
![]() $\Delta \subset \Gamma $
are as in the statement of the corollary. Without loss of generality, we can assume that
$\Delta \subset \Gamma $
are as in the statement of the corollary. Without loss of generality, we can assume that
![]() $\operatorname {\mathrm {Rad}}_p(\Gamma )$
is trivial. Let
$\operatorname {\mathrm {Rad}}_p(\Gamma )$
is trivial. Let
![]() $n:=\overline {\mathrm {rd}}_p(\Gamma )$
. Using the bound
$n:=\overline {\mathrm {rd}}_p(\Gamma )$
. Using the bound
![]() $|{\mathbf {G}}(\mathbb {F}_p)| \leq (p+1)^{{\operatorname {dim}}\, {\mathbf {G}}}$
from [Reference NoriNor87, Lemma 3.5], we may also assume that
$|{\mathbf {G}}(\mathbb {F}_p)| \leq (p+1)^{{\operatorname {dim}}\, {\mathbf {G}}}$
from [Reference NoriNor87, Lemma 3.5], we may also assume that
![]() $p>3$
and
$p>3$
and
![]() $p>{C_{LP0}}(n)$
(otherwise, the claim holds with
$p>{C_{LP0}}(n)$
(otherwise, the claim holds with
![]() $\Delta ^\circ =1$
). Embed
$\Delta ^\circ =1$
). Embed
![]() $\Gamma \hookrightarrow {\mathbf {G}}(\mathbb {F}_p)$
with
$\Gamma \hookrightarrow {\mathbf {G}}(\mathbb {F}_p)$
with
![]() ${\mathbf {G}}$
connected reductive of dimension n. Applying Proposition 4.0.8 to
${\mathbf {G}}$
connected reductive of dimension n. Applying Proposition 4.0.8 to
![]() $\Delta \subset {\mathbf {G}}(\mathbb {F}_p)$
, there is a normal subgroup
$\Delta \subset {\mathbf {G}}(\mathbb {F}_p)$
, there is a normal subgroup
![]() $\Delta ^\circ \triangleleft \Delta $
, a connected reductive group
$\Delta ^\circ \triangleleft \Delta $
, a connected reductive group
![]() ${\mathbf {H}}$
defined over
${\mathbf {H}}$
defined over
![]() $\mathbb {F}_p$
, and a homomorphism
$\mathbb {F}_p$
, and a homomorphism
![]() $\rho : \Delta ^\circ \rightarrow {\mathbf {H}}(\mathbb {F}_p)$
such that
$\rho : \Delta ^\circ \rightarrow {\mathbf {H}}(\mathbb {F}_p)$
such that
-
1.
 $[\Delta : \Delta ^\circ ] \leq {C_{LP0}}(n)$
.
$[\Delta : \Delta ^\circ ] \leq {C_{LP0}}(n)$
. -
2.
 $\ker \rho $
is a p-group.
$\ker \rho $
is a p-group. -
3.
 $\rho (\Delta ^\circ )$
is big in
$\rho (\Delta ^\circ )$
is big in
 ${\mathbf {H}}(\mathbb {F}_p)$
.
${\mathbf {H}}(\mathbb {F}_p)$
. -
4.
 ${\operatorname {dim}}\,{\mathbf {H}} \leq n$
.
${\operatorname {dim}}\,{\mathbf {H}} \leq n$
. -
5. If
 ${\operatorname {dim}}\,{\mathbf {H}} = n$
, then
${\operatorname {dim}}\,{\mathbf {H}} = n$
, then
 $\ker \rho =1$
.
$\ker \rho =1$
.
By Lemma 4.0.12,
![]() $\ker \rho = \operatorname {\mathrm {Rad}}_p(\Delta ^\circ )$
. In particular,
$\ker \rho = \operatorname {\mathrm {Rad}}_p(\Delta ^\circ )$
. In particular,
![]() $\overline {\mathrm {rd}}_p(\Delta ^\circ ) \leq {\operatorname {dim}}\,{\mathbf {H}}$
.
$\overline {\mathrm {rd}}_p(\Delta ^\circ ) \leq {\operatorname {dim}}\,{\mathbf {H}}$
.
If
![]() ${\operatorname {dim}}\,{\mathbf {H}} < n$
, we are done. Otherwise, since
${\operatorname {dim}}\,{\mathbf {H}} < n$
, we are done. Otherwise, since
![]() $[\Delta : \Delta ^\circ ] < {C_{LP0}}(n) < p$
, we get that
$[\Delta : \Delta ^\circ ] < {C_{LP0}}(n) < p$
, we get that
contradicting the condition that
![]() $\operatorname {\mathrm {Rad}}_p(\Delta )\neq \Delta \cap \operatorname {\mathrm {Rad}}_p(\Gamma )$
.
$\operatorname {\mathrm {Rad}}_p(\Delta )\neq \Delta \cap \operatorname {\mathrm {Rad}}_p(\Gamma )$
.
Corollary 4.0.13. There is an increasing function
![]() ${C_{LP}}: \mathbb {N} \rightarrow \mathbb {N}$
for which the following holds. If p is a prime,
${C_{LP}}: \mathbb {N} \rightarrow \mathbb {N}$
for which the following holds. If p is a prime,
![]() $(\Gamma ,\theta )$
is a finite symmetric pair and
$(\Gamma ,\theta )$
is a finite symmetric pair and
![]() $\operatorname {\mathrm {Rad}}_p(\Gamma )=1$
, then there is a
$\operatorname {\mathrm {Rad}}_p(\Gamma )=1$
, then there is a
![]() $\theta $
-invariant normal subgroup
$\theta $
-invariant normal subgroup
![]() $\Delta \triangleleft \Gamma $
satisfying
$\Delta \triangleleft \Gamma $
satisfying
![]() $[\Gamma : \Delta ]<{C_{LP}}(\mathrm {rd}_p(\Gamma ))$
, a connected reductive algebraic group
$[\Gamma : \Delta ]<{C_{LP}}(\mathrm {rd}_p(\Gamma ))$
, a connected reductive algebraic group
![]() ${\mathbf {H}}$
satisfying
${\mathbf {H}}$
satisfying
![]() ${\operatorname {dim}}\, {\mathbf {H}} \leq 2\mathrm {rd}_p(\Gamma )$
, an involution t of
${\operatorname {dim}}\, {\mathbf {H}} \leq 2\mathrm {rd}_p(\Gamma )$
, an involution t of
![]() ${\mathbf {H}}$
and an
${\mathbf {H}}$
and an
![]() $S_2$
-equivariant embedding
$S_2$
-equivariant embedding
![]() $\Delta \subset {\mathbf {H}}(\mathbb {F}_p)$
such that
$\Delta \subset {\mathbf {H}}(\mathbb {F}_p)$
such that
![]() ${\mathbf {H}}(\mathbb {F}_p)' \subset \Delta \subset {\mathbf {H}}(\mathbb {F}_p)$
.
${\mathbf {H}}(\mathbb {F}_p)' \subset \Delta \subset {\mathbf {H}}(\mathbb {F}_p)$
.
Proof. Set
![]() ${C_{LP}}(n)={C_{LP0}}(2n).$
Embed
${C_{LP}}(n)={C_{LP0}}(2n).$
Embed
![]() $\Gamma \hookrightarrow {\mathbf {G}}$
and apply Proposition 4.0.8 to
$\Gamma \hookrightarrow {\mathbf {G}}$
and apply Proposition 4.0.8 to
![]() ${\mathbf {G}} \times {\mathbf {G}}$
, the involution
${\mathbf {G}} \times {\mathbf {G}}$
, the involution
![]() $t(x,y)=(y,x)$
and the subgroup
$t(x,y)=(y,x)$
and the subgroup
![]() $\left\{ (x,\theta (x)) \mid x\in \Gamma \right\}\cong \Gamma $
.
$\left\{ (x,\theta (x)) \mid x\in \Gamma \right\}\cong \Gamma $
.
4.1
 $\theta $
-invariant subgroups of bounded index
$\theta $
-invariant subgroups of bounded index
In this subsection, we prove Corollary 4.1.2, which is a
![]() $S_2$
-equivariant version of the monotonicity of
$S_2$
-equivariant version of the monotonicity of
![]() $\overline {\mathrm {rd}}$
, Corollary 4.0.11.
$\overline {\mathrm {rd}}$
, Corollary 4.0.11.
Lemma 4.1.1. There is a function
![]() $C_{inv}:\mathbb N \times \mathbb N \to \mathbb N$
which is increasing in both variables such that, for any
$C_{inv}:\mathbb N \times \mathbb N \to \mathbb N$
which is increasing in both variables such that, for any
-
• pair of finite groups
 $\Delta <\Gamma $
and
$\Delta <\Gamma $
and -
• a prime p,
there exists a subgroup
![]() $\Delta ^\circ \lhd \Delta $
which is normal in
$\Delta ^\circ \lhd \Delta $
which is normal in
![]() $ \Gamma $
and satisfies
$ \Gamma $
and satisfies
and
Proof. Define recursively
and
We will prove the lemma by induction on
![]() $\overline {\mathrm {rd}}_p(\Delta )$
. For
$\overline {\mathrm {rd}}_p(\Delta )$
. For
![]() $\overline {\mathrm {rd}}_p(\Delta )=0$
, the claim is clear. For the induction step, let
$\overline {\mathrm {rd}}_p(\Delta )=0$
, the claim is clear. For the induction step, let
![]() $n>0$
be an integer and assume the lemma holds if
$n>0$
be an integer and assume the lemma holds if
![]() $\overline {\mathrm {rd}}_p(\Delta )<n$
. We prove the lemma for
$\overline {\mathrm {rd}}_p(\Delta )<n$
. We prove the lemma for
![]() $\overline {\mathrm {rd}}_p(\Delta )=n$
. Let
$\overline {\mathrm {rd}}_p(\Delta )=n$
. Let
 $$ \begin{align*}\Delta_1:=\bigcap_{\gamma\in \Gamma}\gamma \Delta \gamma^{-1}.\end{align*} $$
$$ \begin{align*}\Delta_1:=\bigcap_{\gamma\in \Gamma}\gamma \Delta \gamma^{-1}.\end{align*} $$
We consider the following cases:
-
Case 1.
 $\operatorname {\mathrm {Rad}}_p(\Delta _1)= \operatorname {\mathrm {Rad}}_p(\Delta )\cap \Delta _1$
.
$\operatorname {\mathrm {Rad}}_p(\Delta _1)= \operatorname {\mathrm {Rad}}_p(\Delta )\cap \Delta _1$
.In this case,
 $\overline {\mathrm {rd}}_p(\Delta _1)\leq \overline {\mathrm {rd}}_p(\Delta )=n$
, so we can take
$\overline {\mathrm {rd}}_p(\Delta _1)\leq \overline {\mathrm {rd}}_p(\Delta )=n$
, so we can take
 $\Delta ^\circ := \Delta _1$
, and we are done.
$\Delta ^\circ := \Delta _1$
, and we are done. -
Case 2.
 $\operatorname {\mathrm {Rad}}_p(\Delta _1)\neq \operatorname {\mathrm {Rad}}_p(\Delta )\cap \Delta _1$
.
$\operatorname {\mathrm {Rad}}_p(\Delta _1)\neq \operatorname {\mathrm {Rad}}_p(\Delta )\cap \Delta _1$
.In this case, Corollary 4.0.11 implies that we can find
 $\Delta _2$
such that and
$\Delta _2$
such that and $$ \begin{align*}\overline{\mathrm{rd}}_p(\Delta_2)<\overline{\mathrm{rd}}_p(\Delta)=n\end{align*} $$
By the induction hypothesis, there exists
$$ \begin{align*}\overline{\mathrm{rd}}_p(\Delta_2)<\overline{\mathrm{rd}}_p(\Delta)=n\end{align*} $$
By the induction hypothesis, there exists $$ \begin{align*}[\Delta_1:\Delta_2]\leq C_{mon0}(n).\end{align*} $$
$$ \begin{align*}[\Delta_1:\Delta_2]\leq C_{mon0}(n).\end{align*} $$
 $\Delta ^\circ \lhd \Delta _2$
which is normal in
$\Delta ^\circ \lhd \Delta _2$
which is normal in
 $\Gamma $
and satisfies and
$\Gamma $
and satisfies and $$ \begin{align*}[\Delta_2:\Delta^\circ] \leq C_{inv}(n-1,[\Gamma:\Delta_2])\end{align*} $$
We get
$$ \begin{align*}[\Delta_2:\Delta^\circ] \leq C_{inv}(n-1,[\Gamma:\Delta_2])\end{align*} $$
We get $$ \begin{align*}\overline{\mathrm{rd}}_p(\Delta^\circ)\leq \overline{\mathrm{rd}}_p(\Delta_2)<n.\end{align*} $$
$$ \begin{align*}\overline{\mathrm{rd}}_p(\Delta^\circ)\leq \overline{\mathrm{rd}}_p(\Delta_2)<n.\end{align*} $$
 $$ \begin{align*} [\Gamma:\Delta^\circ] &\leq [\Gamma:\Delta_1]\cdot [\Delta_1:\Delta_2]\cdot [\Delta_2:\Delta^\circ] \\&\leq [\Gamma:\Delta]! C_{mon0}(n) C_{inv}(n-1,[\Gamma:\Delta_2]) \\&\leq [\Gamma:\Delta]! C_{mon0}(n) C_{inv}(n-1,[\Gamma:\Delta_1]\cdot [\Delta_1:\Delta_2]) \\&\leq [\Gamma:\Delta]! C_{mon0}(n) C_{inv}(n-1,[\Gamma:\Delta]! C_{LP}(n))=C_{inv}(n,[\Gamma:\Delta]).\\[-39pt] \end{align*} $$
$$ \begin{align*} [\Gamma:\Delta^\circ] &\leq [\Gamma:\Delta_1]\cdot [\Delta_1:\Delta_2]\cdot [\Delta_2:\Delta^\circ] \\&\leq [\Gamma:\Delta]! C_{mon0}(n) C_{inv}(n-1,[\Gamma:\Delta_2]) \\&\leq [\Gamma:\Delta]! C_{mon0}(n) C_{inv}(n-1,[\Gamma:\Delta_1]\cdot [\Delta_1:\Delta_2]) \\&\leq [\Gamma:\Delta]! C_{mon0}(n) C_{inv}(n-1,[\Gamma:\Delta]! C_{LP}(n))=C_{inv}(n,[\Gamma:\Delta]).\\[-39pt] \end{align*} $$
The last lemma and Corollary 4.0.11 imply the following:
Corollary 4.1.2. There is a function
![]() $C_{mon}:\mathbb N \to \mathbb N$
such that, for any odd prime p, any finite group
$C_{mon}:\mathbb N \to \mathbb N$
such that, for any odd prime p, any finite group
![]() $\Gamma $
, any subgroup
$\Gamma $
, any subgroup
![]() $\Delta < \Gamma $
satisfying
$\Delta < \Gamma $
satisfying
![]() $\operatorname {\mathrm {Rad}}_p(\Delta )\neq \Delta \cap \operatorname {\mathrm {Rad}}_p(\Gamma )$
, and any involution
$\operatorname {\mathrm {Rad}}_p(\Delta )\neq \Delta \cap \operatorname {\mathrm {Rad}}_p(\Gamma )$
, and any involution
![]() $\theta $
of
$\theta $
of
![]() $\Delta $
, there is a normal
$\Delta $
, there is a normal
![]() $\theta $
-invariant subgroup
$\theta $
-invariant subgroup
![]() $\Delta ^\circ \lhd \Delta $
such that
$\Delta ^\circ \lhd \Delta $
such that
-
•
 $\overline {\mathrm {rd}}_p(\Delta ^\circ ) < \overline {\mathrm {rd}}_p (\Gamma ).$
$\overline {\mathrm {rd}}_p(\Delta ^\circ ) < \overline {\mathrm {rd}}_p (\Gamma ).$
-
•
 $[\Delta :\Delta ^\circ ]\leq C_{mon}(\overline {\mathrm {rd}}_p(\Gamma )).$
$[\Delta :\Delta ^\circ ]\leq C_{mon}(\overline {\mathrm {rd}}_p(\Gamma )).$
Proof. Set
By the monotonicity of the
![]() $\overline {\mathrm {rd}}_p$
(Corollary 4.0.11), we can find
$\overline {\mathrm {rd}}_p$
(Corollary 4.0.11), we can find
![]() $\Delta _1\lhd \Delta $
satisfying
$\Delta _1\lhd \Delta $
satisfying
and
Let
![]() $\tilde \Delta :=\langle \theta \rangle \ltimes \Delta $
. By Lemma 4.1.1, there is a normal subgroup
$\tilde \Delta :=\langle \theta \rangle \ltimes \Delta $
. By Lemma 4.1.1, there is a normal subgroup
![]() $\Delta ^\circ \lhd \Delta _1$
which is also normal in
$\Delta ^\circ \lhd \Delta _1$
which is also normal in
![]() $\tilde \Delta $
and satisfies
$\tilde \Delta $
and satisfies
and
The fact that
![]() $\Delta ^\circ $
is normal in
$\Delta ^\circ $
is normal in
![]() $\tilde \Delta $
implies that
$\tilde \Delta $
implies that
![]() $\Delta ^\circ $
is
$\Delta ^\circ $
is
![]() $\theta $
-invariant. We also have
$\theta $
-invariant. We also have
 $$ \begin{align*} [\Delta:\Delta^\circ]&\leq [\tilde \Delta:\Delta^\circ] \leq C_{inv}(\overline{\mathrm{rd}}_p(\Delta_1),[\tilde \Delta:\Delta_1]) \\&\leq C_{inv}(\overline{\mathrm{rd}}_p(\Gamma),[\tilde \Delta:\Delta_1]) = C_{inv}(\overline{\mathrm{rd}}_p(\Gamma),2[\Delta:\Delta_1]) \\&\leq C_{inv}(\overline{\mathrm{rd}}_p(\Gamma),2C_{mon0}(\overline{\mathrm{rd}}_p(\Gamma)))= C_{mon}(\overline{\mathrm{rd}}_p(\Gamma)).\\[-41pt] \end{align*} $$
$$ \begin{align*} [\Delta:\Delta^\circ]&\leq [\tilde \Delta:\Delta^\circ] \leq C_{inv}(\overline{\mathrm{rd}}_p(\Delta_1),[\tilde \Delta:\Delta_1]) \\&\leq C_{inv}(\overline{\mathrm{rd}}_p(\Gamma),[\tilde \Delta:\Delta_1]) = C_{inv}(\overline{\mathrm{rd}}_p(\Gamma),2[\Delta:\Delta_1]) \\&\leq C_{inv}(\overline{\mathrm{rd}}_p(\Gamma),2C_{mon0}(\overline{\mathrm{rd}}_p(\Gamma)))= C_{mon}(\overline{\mathrm{rd}}_p(\Gamma)).\\[-41pt] \end{align*} $$
5 Groups of odd order
In this section, we analyze symmetric pairs of groups of odd order and prove several statements about them that will be used in the proof of the main theorem. In particular, we prove a strong version of the main theorem for symmetric pairs of groups of odd order. Namely, we prove that they are all Gelfand pairs (Corollary 5.0.5(1)).
We also prove some other results for symmetric pairs of groups of odd order; see Lemma 5.0.2 and Corollary 5.0.5(2).
Remark 5.0.1.
-
1. Even though the results in this section are valid for arbitrary groups of odd order, we will only use them for p-groups for odd p.
-
2. All the proofs in this section are based on the fact that, for a group of odd order n, the map
 $x\mapsto x^{\frac {n+1}{2}}$
is a square root.
$x\mapsto x^{\frac {n+1}{2}}$
is a square root.
The following is a special case of the Schur–Zassenhaus theorem:
Lemma 5.0.2. If
![]() $\Omega $
is a finite group of odd order and
$\Omega $
is a finite group of odd order and
![]() $\theta $
is its involution, then
$\theta $
is its involution, then
![]() $H^1(S_2,\Omega )=1$
.
$H^1(S_2,\Omega )=1$
.
Proof. We need to show that, for every element
![]() $s\in \Omega $
that satisfies
$s\in \Omega $
that satisfies
![]() $s=\theta (s^{-1})$
, there exists an element
$s=\theta (s^{-1})$
, there exists an element
![]() $g\in \Omega $
such that
$g\in \Omega $
such that
![]() $s=\theta (g^{-1})g$
.
$s=\theta (g^{-1})g$
.
Let
![]() $g=s^{\frac {|\Omega |+1}{2}}.$
Then
$g=s^{\frac {|\Omega |+1}{2}}.$
Then
Lemma 5.0.3 (Gelfand-Kazhdan property for symmetric pairs of odd order).
If
![]() $\Omega $
is a finite group of odd order and
$\Omega $
is a finite group of odd order and
![]() $\theta : \Omega \rightarrow \Omega $
is an involution, then, for any
$\theta : \Omega \rightarrow \Omega $
is an involution, then, for any
![]() $g\in \Omega $
, there are
$g\in \Omega $
, there are
![]() $h_1,h_2\in \Omega ^\theta $
such that
$h_1,h_2\in \Omega ^\theta $
such that
![]() $h_1 g h_2=\theta (g^{-1})$
.
$h_1 g h_2=\theta (g^{-1})$
.
Lemma 5.0.3 follows immediately from the following:
Lemma 5.0.4 (polar decomposition for symmetric pairs of odd order.)
If
![]() $\Omega $
is a finite group of odd order and
$\Omega $
is a finite group of odd order and
![]() $\theta : \Omega \rightarrow \Omega $
is an involution, then
$\theta : \Omega \rightarrow \Omega $
is an involution, then
where
![]() $\Omega ^{\theta \circ inv}:=\{g\in \Omega |\theta (g)=g^{-1}\}$
.
$\Omega ^{\theta \circ inv}:=\{g\in \Omega |\theta (g)=g^{-1}\}$
.
Proof. Let
![]() $g\in \Omega $
. Define
$g\in \Omega $
. Define
![]() $s=(\theta (g^{-1})g)^{\frac {|\Omega |+1}{2}}$
and
$s=(\theta (g^{-1})g)^{\frac {|\Omega |+1}{2}}$
and
![]() $o=gs^{-1}$
. Then,
$o=gs^{-1}$
. Then,
 $$ \begin{align*} \theta(s)&=\theta((\theta(g^{-1})g)^{\frac{|\Omega|+1}{2}})\\&= (\theta(\theta(g^{-1})g))^{\frac{|\Omega|+1}{2}}\\&=(g^{-1})\theta(g))^{\frac{|\Omega|+1}{2}}\\&=((\theta(g^{-1}) g)^{-1})^{\frac{|\Omega|+1}{2}}\\&=((\theta(g^{-1}) g)^{\frac{|\Omega|+1}{2}})^{-1})=s^{-1},\\\theta(o)&=\theta(gs^{-1})=\theta(g)s\\&=\theta(g)(\theta(g^{-1})g)^{\frac{|\Omega|+1}{2}}\\&=\theta(g)\theta(g^{-1})g(\theta(g^{-1})g)^{\frac{|\Omega|+1}{2}-1}\\&=g(\theta(g^{-1})g)^{\frac{|\Omega|+1}{2}-1}\\&=g(\theta(g^{-1})g)^{\frac{|\Omega|-1}{2}}\\&=g(\theta(g^{-1})g)^{|\Omega|-\frac{|\Omega|+1}{2}}\\&=g(\theta(g^{-1})g)^{-\frac{|\Omega|+1}{2}}=gs^{-1}=o \end{align*} $$
$$ \begin{align*} \theta(s)&=\theta((\theta(g^{-1})g)^{\frac{|\Omega|+1}{2}})\\&= (\theta(\theta(g^{-1})g))^{\frac{|\Omega|+1}{2}}\\&=(g^{-1})\theta(g))^{\frac{|\Omega|+1}{2}}\\&=((\theta(g^{-1}) g)^{-1})^{\frac{|\Omega|+1}{2}}\\&=((\theta(g^{-1}) g)^{\frac{|\Omega|+1}{2}})^{-1})=s^{-1},\\\theta(o)&=\theta(gs^{-1})=\theta(g)s\\&=\theta(g)(\theta(g^{-1})g)^{\frac{|\Omega|+1}{2}}\\&=\theta(g)\theta(g^{-1})g(\theta(g^{-1})g)^{\frac{|\Omega|+1}{2}-1}\\&=g(\theta(g^{-1})g)^{\frac{|\Omega|+1}{2}-1}\\&=g(\theta(g^{-1})g)^{\frac{|\Omega|-1}{2}}\\&=g(\theta(g^{-1})g)^{|\Omega|-\frac{|\Omega|+1}{2}}\\&=g(\theta(g^{-1})g)^{-\frac{|\Omega|+1}{2}}=gs^{-1}=o \end{align*} $$
and, thus,
Lemma 5.0.3 gives the following:
Corollary 5.0.5. If
![]() $\Gamma $
is a finite group of odd order and
$\Gamma $
is a finite group of odd order and
![]() $\theta $
is an involution of
$\theta $
is an involution of
![]() $\Omega $
, then
$\Omega $
, then
-
1. (Gelfand property for symmetric pairs of odd order:)
 $(\Omega ,\Omega ^ \theta )$
is a Gelfand pair – that is, for any
$(\Omega ,\Omega ^ \theta )$
is a Gelfand pair – that is, for any
 $\rho \in \operatorname {Irr}(\Omega )$
,
$\rho \in \operatorname {Irr}(\Omega )$
,  $$ \begin{align*}{\operatorname{dim}}\rho^{\Omega^\theta}\leq 1.\end{align*} $$
$$ \begin{align*}{\operatorname{dim}}\rho^{\Omega^\theta}\leq 1.\end{align*} $$
-
2. (Lapid-Prasad property for symmetric pairs of odd order:) Any representation
 $\rho $
of G which is
$\rho $
of G which is
 $\Omega ^ \theta $
distinguished (i.e., satisfies
$\Omega ^ \theta $
distinguished (i.e., satisfies
 ${\operatorname {dim}}\rho ^{\Omega ^\theta }>0$
) also satisfies
${\operatorname {dim}}\rho ^{\Omega ^\theta }>0$
) also satisfies  $$ \begin{align*}\rho^*\simeq\rho\circ \theta.\end{align*} $$
$$ \begin{align*}\rho^*\simeq\rho\circ \theta.\end{align*} $$
Proof. The claims follow from Lemma 5.0.3 and [Reference AizenbudAiz, Theorem 2] (which is an adaptation of results from [Reference Gel’fand and KazhdanGK75] and [Reference Jacquet and RallisJR96]).
6 Bounds on
 $H^1(S_2,\Gamma )$
$H^1(S_2,\Gamma )$
In this section, we prove Corollary 6.0.6, which gives bounds on the cohomology group
![]() $H^1(S_2,\Delta )$
for a finite symmetric pair
$H^1(S_2,\Delta )$
for a finite symmetric pair
![]() $(\Delta ,\theta )$
.
$(\Delta ,\theta )$
.
Lemma 6.0.1. There is an increasing function
![]() $C_{H1R0}:\mathbb N\to \mathbb N$
such that, for any finite field F of odd characteristic, any connected reductive group
$C_{H1R0}:\mathbb N\to \mathbb N$
such that, for any finite field F of odd characteristic, any connected reductive group
![]() ${\mathbf {G}}$
and any involution t of
${\mathbf {G}}$
and any involution t of
![]() ${\mathbf {G}}$
, both defined over F,
${\mathbf {G}}$
, both defined over F,
Proof. Let n be an integer. Let
![]() $\Phi _n:{\mathcal R}_n\to {\mathcal S}_n$
and
$\Phi _n:{\mathcal R}_n\to {\mathcal S}_n$
and
![]() $\tau _n$
be as in Lemma 3.2.1. Let
$\tau _n$
be as in Lemma 3.2.1. Let
![]() $s_n$
be the anti-automorphism
$s_n$
be the anti-automorphism
![]() $s_n(g):=\tau _n(g^{-1})$
. Let
$s_n(g):=\tau _n(g^{-1})$
. Let
![]() $C_{H1R0}(n)$
be such that, for any geometric point x of
$C_{H1R0}(n)$
be such that, for any geometric point x of
![]() ${\mathcal S}_n$
,
${\mathcal S}_n$
,
Fix
![]() $x\in {\mathcal S}_n(F)$
and let
$x\in {\mathcal S}_n(F)$
and let
![]() ${\mathbf {G}}:=\Phi _n^{-1}(x)$
. We need to show that
${\mathbf {G}}:=\Phi _n^{-1}(x)$
. We need to show that
By definition, we have
![]() $H^1(S_2,{\mathbf {G}}(F))={\mathbf {G}}(F)^{s_n}/{\mathbf {G}}(F)$
, where the action of
$H^1(S_2,{\mathbf {G}}(F))={\mathbf {G}}(F)^{s_n}/{\mathbf {G}}(F)$
, where the action of
![]() ${\mathbf {G}}$
on
${\mathbf {G}}$
on
![]() ${\mathbf {G}}^{s_n}$
is given by
${\mathbf {G}}^{s_n}$
is given by
![]() $g \cdot x:=gx s_n(g).$
Since
$g \cdot x:=gx s_n(g).$
Since
![]() ${\mathbf {G}}$
is connected, Lang’s theorem implies that the map
${\mathbf {G}}$
is connected, Lang’s theorem implies that the map
![]() ${\mathbf {G}}(F)^{s_n}/{\mathbf {G}}(F)\to ({\mathbf {G}}^{s_n}/{\mathbf {G}})(F)$
is an embedding. By analyzing the action of the Lie algebra, it is easy to see that the orbits of the action of
${\mathbf {G}}(F)^{s_n}/{\mathbf {G}}(F)\to ({\mathbf {G}}^{s_n}/{\mathbf {G}})(F)$
is an embedding. By analyzing the action of the Lie algebra, it is easy to see that the orbits of the action of
![]() ${\mathbf {G}}$
on
${\mathbf {G}}$
on
![]() ${\mathbf {G}}^{s_n}$
are open. Thus,
${\mathbf {G}}^{s_n}$
are open. Thus,
The following lemmas are straightforward:
Lemma 6.0.2. Let A be a finite abelian group with an action of
![]() $S_2$
. Denote
$S_2$
. Denote
![]() $A[2]=\left\{ x\in A \mid x^2=0 \right\}$
. Then
$A[2]=\left\{ x\in A \mid x^2=0 \right\}$
. Then
![]() $|H^1(S_2,A)|\leq |A[2]|^2$
.
$|H^1(S_2,A)|\leq |A[2]|^2$
.
Proof. Let
![]() $\theta \in \operatorname {\mathrm {Aut}}(A)$
be the nontrivial element of
$\theta \in \operatorname {\mathrm {Aut}}(A)$
be the nontrivial element of
![]() $S_2$
. Denote
$S_2$
. Denote
![]() $C=\left\{ x\in A \mid x \theta (x)=1 \right\}$
,
$C=\left\{ x\in A \mid x \theta (x)=1 \right\}$
,
![]() $B=\left\{ x ^{-1} \theta (x) \mid x\in A \right\}$
and
$B=\left\{ x ^{-1} \theta (x) \mid x\in A \right\}$
and
![]() $S=\left\{ x^2 \mid x\in A \right\}$
. We need to show that
$S=\left\{ x^2 \mid x\in A \right\}$
. We need to show that
![]() $|C/B| \leq |A[2]|^2$
. Since
$|C/B| \leq |A[2]|^2$
. Since
![]() $|C/B| = |C/C\cap S| \cdot |C \cap S / B\cap S| \leq |A[2]|\cdot |C \cap S / B\cap S|$
, it in enough to show that
$|C/B| = |C/C\cap S| \cdot |C \cap S / B\cap S| \leq |A[2]|\cdot |C \cap S / B\cap S|$
, it in enough to show that
![]() $|C \cap S / B\cap S| \leq |A[2]|$
.
$|C \cap S / B\cap S| \leq |A[2]|$
.
Let
![]() $x\in C\cap S$
and let
$x\in C\cap S$
and let
![]() $z\in A$
be such that
$z\in A$
be such that
![]() $z^2=x$
. Then
$z^2=x$
. Then
![]() $z \theta (z)\in A[2]$
and
$z \theta (z)\in A[2]$
and
![]() $x \left( z ^{-1} \theta (z) \right) = z \theta (z)\in A[2]$
. Hence,
$x \left( z ^{-1} \theta (z) \right) = z \theta (z)\in A[2]$
. Hence,
![]() $C\cap S \subseteq A[2] \cdot B$
, so
$C\cap S \subseteq A[2] \cdot B$
, so
![]() $|C \cap S / B\cap S| \leq |A[2] \cdot B / B| \leq |A[2]|$
.
$|C \cap S / B\cap S| \leq |A[2] \cdot B / B| \leq |A[2]|$
.
Lemma 6.0.3. Let
![]() $\Gamma $
be a finite group, let
$\Gamma $
be a finite group, let
![]() $\theta $
be an involution of
$\theta $
be an involution of
![]() $\Gamma $
and let
$\Gamma $
and let
![]() $N\triangleleft \Gamma $
be a normal
$N\triangleleft \Gamma $
be a normal
![]() $\theta $
-invariant subgroup. Then
$\theta $
-invariant subgroup. Then
-
1.
 $|H^1(S_2, N)| \leq |H^1(S_2,\Gamma )| \cdot [\Gamma : N]$
.
$|H^1(S_2, N)| \leq |H^1(S_2,\Gamma )| \cdot [\Gamma : N]$
. -
2.
where $$\begin{align*}|H^1(S_2,\Gamma)| \leq |H^1(S_2,\Gamma/N)| \cdot \max_{\tau}|H_\tau^1(S_2,N)|, \end{align*}$$
$$\begin{align*}|H^1(S_2,\Gamma)| \leq |H^1(S_2,\Gamma/N)| \cdot \max_{\tau}|H_\tau^1(S_2,N)|, \end{align*}$$
 $\tau $
ranges over all involutions of N (including
$\tau $
ranges over all involutions of N (including
 $\tau =1$
) and
$\tau =1$
) and
 $H_\tau ^1(S_2,N)$
is the cohomology of the
$H_\tau ^1(S_2,N)$
is the cohomology of the
 $S_2$
-module N given by the involution
$S_2$
-module N given by the involution
 $\tau $
.
$\tau $
.
Proof. In the proof, if G is a group with involution
![]() $\sigma $
, we identify
$\sigma $
, we identify
![]() $H^1(S_2,G)$
with the quotient of
$H^1(S_2,G)$
with the quotient of
![]() $C_{G,\sigma }:=\left\{ x\in G \mid x \sigma (x)=1 \right\}$
by the action of G given by
$C_{G,\sigma }:=\left\{ x\in G \mid x \sigma (x)=1 \right\}$
by the action of G given by
![]() $g \cdot x= \sigma (g)x g ^{-1}$
.
$g \cdot x= \sigma (g)x g ^{-1}$
.
-
1. We have have a map
 $\alpha :C_{N,\theta } / N \rightarrow C_{\Gamma ,\theta } / \Gamma $
taking
$\alpha :C_{N,\theta } / N \rightarrow C_{\Gamma ,\theta } / \Gamma $
taking
 $N \cdot x$
to
$N \cdot x$
to
 $\Gamma \cdot x$
. Given
$\Gamma \cdot x$
. Given
 $x\in C_{N,\theta }$
, the fiber
$x\in C_{N,\theta }$
, the fiber
 $\alpha ^{-1} (\alpha (N \cdot x))=\alpha ^{-1} (\Gamma \cdot x)$
is equal to
$\alpha ^{-1} (\alpha (N \cdot x))=\alpha ^{-1} (\Gamma \cdot x)$
is equal to
 $(\Gamma \cdot x) / N$
, so its size is at most
$(\Gamma \cdot x) / N$
, so its size is at most
 $[\Gamma : N]$
. Hence,
$[\Gamma : N]$
. Hence,
 $|C_{N,\theta } / N| \leq |C_{\Gamma ,\theta } / \Gamma | \cdot [\Gamma : N]$
.
$|C_{N,\theta } / N| \leq |C_{\Gamma ,\theta } / \Gamma | \cdot [\Gamma : N]$
. -
2. We have a map
 $\beta :C_{\Gamma ,\theta }/\Gamma \rightarrow C_{\Gamma /N,\theta }/ (\Gamma /N) $
sending
$\beta :C_{\Gamma ,\theta }/\Gamma \rightarrow C_{\Gamma /N,\theta }/ (\Gamma /N) $
sending
 $\Gamma \cdot x$
to
$\Gamma \cdot x$
to
 $(\Gamma / N) \cdot (xN)$
. It is enough to show that the sizes of the fibers of
$(\Gamma / N) \cdot (xN)$
. It is enough to show that the sizes of the fibers of
 $\beta $
are bounded by
$\beta $
are bounded by
 $\max _{\tau }|H_\tau ^1(S_2,N)|$
.
$\max _{\tau }|H_\tau ^1(S_2,N)|$
.For
 $x\in C_{\Gamma ,\theta }$
, let
$x\in C_{\Gamma ,\theta }$
, let
 $\tau _x:N \rightarrow N$
be the automorphism
$\tau _x:N \rightarrow N$
be the automorphism
 $\tau _x(n)=x ^{-1} \theta (n) x$
. Since
$\tau _x(n)=x ^{-1} \theta (n) x$
. Since
 $\tau _x^2(n)=x ^{-1} \theta (x ^{-1}) n \theta (x)x=n$
, the automorphism
$\tau _x^2(n)=x ^{-1} \theta (x ^{-1}) n \theta (x)x=n$
, the automorphism
 $\tau _x$
is an involution.
$\tau _x$
is an involution.Suppose that
 $y\in C_{\Gamma ,\theta }$
and
$y\in C_{\Gamma ,\theta }$
and
 $\beta (\Gamma \cdot x)=\beta (\Gamma \cdot y)$
. Then there is
$\beta (\Gamma \cdot x)=\beta (\Gamma \cdot y)$
. Then there is
 $y'\in \Gamma \cdot y$
such that
$y'\in \Gamma \cdot y$
such that
 $y'=x n$
, for some
$y'=x n$
, for some
 $n\in N$
. Since
$n\in N$
. Since  $$ \begin{align*}1=\theta(y')y'=\theta(x)\theta(n)x n=\theta(x) x x ^{-1} \theta(n) x n= \tau_x(n)n,\end{align*} $$
$$ \begin{align*}1=\theta(y')y'=\theta(x)\theta(n)x n=\theta(x) x x ^{-1} \theta(n) x n= \tau_x(n)n,\end{align*} $$
we get that
 $n\in C_{N,\tau _x}$
. Hence,
$n\in C_{N,\tau _x}$
. Hence,
 $\beta ^{-1} (\beta (\Gamma \cdot x) )$
can be identified with
$\beta ^{-1} (\beta (\Gamma \cdot x) )$
can be identified with
 $xC_{N,\tau _x}/ \Gamma $
. For any
$xC_{N,\tau _x}/ \Gamma $
. For any
 $m\in N$
,
$m\in N$
,  $$\begin{align*}m \cdot y'=\theta(m) x n m ^{-1} = x \tau_x(m) n m ^{-1}, \end{align*}$$
$$\begin{align*}m \cdot y'=\theta(m) x n m ^{-1} = x \tau_x(m) n m ^{-1}, \end{align*}$$
so
 $|\beta ^{-1} (\beta (\Gamma \cdot x) )| \leq |xC_{N,\tau _x} / N |=|H^1_{\tau _x}(S_2,N)|$
.
$|\beta ^{-1} (\beta (\Gamma \cdot x) )| \leq |xC_{N,\tau _x} / N |=|H^1_{\tau _x}(S_2,N)|$
.
Now Lemma 6.0.1 implies the following:
Corollary 6.0.4. There is an increasing function
![]() $C_{H1R}:\mathbb N\to \mathbb N$
such that, for any prime p, any connected semi-simple group
$C_{H1R}:\mathbb N\to \mathbb N$
such that, for any prime p, any connected semi-simple group
![]() ${\mathbf {G}}$
, defined over
${\mathbf {G}}$
, defined over
![]() $\mathbb {F}_p$
, any involution
$\mathbb {F}_p$
, any involution
![]() $\theta $
of
$\theta $
of
![]() ${\mathbf {G}}(\mathbb {F}_p)'$
, we have
${\mathbf {G}}(\mathbb {F}_p)'$
, we have
Proof. Take
![]() $C_{H1R}(n)=C_{H1R0}({\operatorname {dim}} {\mathbf {G}})4^{{\operatorname {dim}} G}$
, where
$C_{H1R}(n)=C_{H1R0}({\operatorname {dim}} {\mathbf {G}})4^{{\operatorname {dim}} G}$
, where
![]() $C_{H1R0}$
is the function given by Lemma 6.0.1.
$C_{H1R0}$
is the function given by Lemma 6.0.1.
Using the bound
![]() $|{\mathbf {G}}(\mathbb {F}_p)| \leq (p+1)^{{\operatorname {dim}}\, {\mathbf {G}}}$
from [Reference NoriNor87, Lemma 3.5], we can assume that
$|{\mathbf {G}}(\mathbb {F}_p)| \leq (p+1)^{{\operatorname {dim}}\, {\mathbf {G}}}$
from [Reference NoriNor87, Lemma 3.5], we can assume that
![]() $p>3$
.
$p>3$
.
Let
![]() $\bar {\mathbf {G}}:={\mathbf {G}}/Z({\mathbf {G}})$
. By Corollary 3.1.3, the induced map
$\bar {\mathbf {G}}:={\mathbf {G}}/Z({\mathbf {G}})$
. By Corollary 3.1.3, the induced map
![]() ${\mathbf {G}}(\mathbb {F}_p)'\to \bar {\mathbf {G}}(\mathbb {F}_p)'$
is onto, and its kernel is
${\mathbf {G}}(\mathbb {F}_p)'\to \bar {\mathbf {G}}(\mathbb {F}_p)'$
is onto, and its kernel is
![]() $Z({\mathbf {G}}(\mathbb {F}_p)')$
. Let
$Z({\mathbf {G}}(\mathbb {F}_p)')$
. Let
![]() $\bar \theta $
be the involution induced by
$\bar \theta $
be the involution induced by
![]() $\theta $
on
$\theta $
on
![]() $\bar {\mathbf {G}}(\mathbb {F}_p)'$
. By Theorem 3.1.10, we can lift
$\bar {\mathbf {G}}(\mathbb {F}_p)'$
. By Theorem 3.1.10, we can lift
![]() $\bar \theta $
to an involution t of
$\bar \theta $
to an involution t of
![]() $\bar {\mathbf {G}}$
. By Lemmas 6.0.3, 6.0.1, 3.1.6 and Theorem 3.1.1, we have
$\bar {\mathbf {G}}$
. By Lemmas 6.0.3, 6.0.1, 3.1.6 and Theorem 3.1.1, we have
 $$ \begin{align*} |H^1(S_2,{\mathbf{G}}(\mathbb{F}_p)')|& \overset{{6.0.3}}{\leq} |H^1(S_2,\bar {\mathbf{G}}(\mathbb{F}_p)')| \max_\tau |H^1_\tau(S_2,Z({\mathbf{G}}(\mathbb{F}_p)'))| {\leq} |H^1(S_2,\bar {\mathbf{G}}(\mathbb{F}_p)')| \cdot |Z({\mathbf{G}}(\mathbb{F}_p)')|\\& \overset{{3.1.1}}{\leq} |H^1(S_2,\bar {\mathbf{G}}(\mathbb{F}_p)')| 2^{{\operatorname{dim}} G} \overset{{6.0.3}}{\leq} |H^1_t(S_2,\bar {\mathbf{G}}(\mathbb{F}_p))|\cdot [\bar {\mathbf{G}}(\mathbb{F}_p):\bar {\mathbf{G}}(\mathbb{F}_p)'] 2^{{\operatorname{dim}} G}\\& \overset{{3.1.6}}{\leq} |H^1_t(S_2,\bar {\mathbf{G}}(\mathbb{F}_p))|\cdot 4^{{\operatorname{dim}} G} \overset{{6.0.1}}{<} C_{H1R0}({\operatorname{dim}} {\mathbf{G}})4^{{\operatorname{dim}} G}=C_{H1R}({\operatorname{dim}} {\mathbf{G}}).\\[-42pt] \end{align*} $$
$$ \begin{align*} |H^1(S_2,{\mathbf{G}}(\mathbb{F}_p)')|& \overset{{6.0.3}}{\leq} |H^1(S_2,\bar {\mathbf{G}}(\mathbb{F}_p)')| \max_\tau |H^1_\tau(S_2,Z({\mathbf{G}}(\mathbb{F}_p)'))| {\leq} |H^1(S_2,\bar {\mathbf{G}}(\mathbb{F}_p)')| \cdot |Z({\mathbf{G}}(\mathbb{F}_p)')|\\& \overset{{3.1.1}}{\leq} |H^1(S_2,\bar {\mathbf{G}}(\mathbb{F}_p)')| 2^{{\operatorname{dim}} G} \overset{{6.0.3}}{\leq} |H^1_t(S_2,\bar {\mathbf{G}}(\mathbb{F}_p))|\cdot [\bar {\mathbf{G}}(\mathbb{F}_p):\bar {\mathbf{G}}(\mathbb{F}_p)'] 2^{{\operatorname{dim}} G}\\& \overset{{3.1.6}}{\leq} |H^1_t(S_2,\bar {\mathbf{G}}(\mathbb{F}_p))|\cdot 4^{{\operatorname{dim}} G} \overset{{6.0.1}}{<} C_{H1R0}({\operatorname{dim}} {\mathbf{G}})4^{{\operatorname{dim}} G}=C_{H1R}({\operatorname{dim}} {\mathbf{G}}).\\[-42pt] \end{align*} $$
Now we can derive our bound on the first cohomology:
Proposition 6.0.5. There is a function
![]() $C_{H1}:\mathbb N\to \mathbb N$
such that for any finite group
$C_{H1}:\mathbb N\to \mathbb N$
such that for any finite group
![]() $\Gamma $
, any involution
$\Gamma $
, any involution
![]() $\theta $
of
$\theta $
of
![]() $\Gamma $
and any prime
$\Gamma $
and any prime
![]() $p>2$
, we have
$p>2$
, we have
Proof. We take
where
![]() $C_{H1R}$
is the function given by Corollary 6.0.4 and
$C_{H1R}$
is the function given by Corollary 6.0.4 and
![]() ${C_{LP}}$
is the function given by Corollary 4.0.13.
${C_{LP}}$
is the function given by Corollary 4.0.13.
Using the bound
![]() $|{\mathbf {G}}(\mathbb {F}_p)| \leq (p+1)^{{\operatorname {dim}}\, {\mathbf {G}}}$
from [Reference NoriNor87, Lemma 3.5] and Lemmas 5.0.2, 6.0.3, we may assume that
$|{\mathbf {G}}(\mathbb {F}_p)| \leq (p+1)^{{\operatorname {dim}}\, {\mathbf {G}}}$
from [Reference NoriNor87, Lemma 3.5] and Lemmas 5.0.2, 6.0.3, we may assume that
![]() $p>3.$
$p>3.$
Let
![]() $\bar \theta $
be the involution of
$\bar \theta $
be the involution of
![]() $\Gamma /\operatorname {\mathrm {Rad}}_p(\Gamma )$
induced by
$\Gamma /\operatorname {\mathrm {Rad}}_p(\Gamma )$
induced by
![]() $\theta $
. By Corollary 4.0.13, there is a
$\theta $
. By Corollary 4.0.13, there is a
![]() $\bar \theta $
-invariant normal subgroup
$\bar \theta $
-invariant normal subgroup
![]() $\Delta $
of
$\Delta $
of
![]() $\Gamma /\operatorname {\mathrm {Rad}}_p(\Gamma )$
, a connected reductive group
$\Gamma /\operatorname {\mathrm {Rad}}_p(\Gamma )$
, a connected reductive group
![]() ${\mathbf {H}}$
defined over
${\mathbf {H}}$
defined over
![]() $\mathbb {F}_p$
and an involution t of
$\mathbb {F}_p$
and an involution t of
![]() ${\mathbf {H}}$
such that
${\mathbf {H}}$
such that
-
•
 $[\Gamma /\operatorname {\mathrm {Rad}}_p(\Gamma ):\Delta ]\leq C_{LP}(\overline {\mathrm {rd}}(\Gamma ))$
,
$[\Gamma /\operatorname {\mathrm {Rad}}_p(\Gamma ):\Delta ]\leq C_{LP}(\overline {\mathrm {rd}}(\Gamma ))$
, -
•
 ${\operatorname {dim}}\, {\mathbf {H}}\leq 2\overline {\mathrm {rd}}(\Gamma )$
,
${\operatorname {dim}}\, {\mathbf {H}}\leq 2\overline {\mathrm {rd}}(\Gamma )$
, -
• There is an equivariant embedding
 $(\Delta ,\bar \theta |_\Delta )\hookrightarrow ({\mathbf {H}}(\mathbb {F}_p),t)$
,
$(\Delta ,\bar \theta |_\Delta )\hookrightarrow ({\mathbf {H}}(\mathbb {F}_p),t)$
, -
•
 ${\mathbf {H}}(\mathbb {F}_p)'<\Delta < {\mathbf {H}}(\mathbb {F}_p)$
.
${\mathbf {H}}(\mathbb {F}_p)'<\Delta < {\mathbf {H}}(\mathbb {F}_p)$
.
By Corollary 3.1.4, we have
![]() $\Delta '={\mathbf {H}}(\mathbb {F}_p)'$
.
$\Delta '={\mathbf {H}}(\mathbb {F}_p)'$
.
Applying Theorem 3.1.1, Corollary 6.0.4 and Lemmas 5.0.2, 6.0.2, 6.0.3, we get
 $$ \begin{align*} |H^1(S_2,\Gamma)| &\overset{{6.0.3}}{\leq} |H^1(S_2,\Gamma/\operatorname{\mathrm{Rad}}_p(\Gamma))| \cdot \max_{\tau} |H^1_\tau(S_2,\operatorname{\mathrm{Rad}}_p(\Gamma))|\overset{{5.0.2} }{=} |H^1(S_2,\Gamma/\operatorname{\mathrm{Rad}}_p(\Gamma))| \\&\overset{{6.0.3}}{\leq} \max_{\tau}|H^1_\tau(S_2,\Delta)| \cdot |H^1(S_2,(\Gamma/(\operatorname{\mathrm{Rad}}_p(\Gamma))/\Delta))| \\&\overset{{6.0.3}}{\leq} \max_{\tau} |H^1_{\tau}(S_2,\Delta)| \cdot [\Gamma/\operatorname{\mathrm{Rad}}_p(\Gamma):\Delta] \\&\overset{\quad\,\,\,\,\,}{\leq} \max_{\tau}|H^1_\tau(S_2,\Delta)| C_{LP}(\overline{\mathrm{rd}}(\Gamma)) \\& \overset{{6.0.3}}{\leq} \max_{\sigma} |H^1_\sigma(S_2,\Delta')| \cdot \max_{\tau} |H^1_\tau(S_2,\Delta / \Delta')| \cdot C_{LP}(\overline{\mathrm{rd}}(\Gamma)) \\& \overset{{6.0.2}}{\leq} \max_{\sigma} |H^1_\sigma(S_2,{\mathbf{H}}(\mathbb{F}_p)')| \cdot | \left( \Delta / \Delta' \right)[2]|^2 \cdot C_{LP}(\overline{\mathrm{rd}}(\Gamma)) \\& \overset{{6.0.4}}{\leq} C_{H1R}(2\overline{\mathrm{rd}}(\Gamma)) \cdot | \left( \Delta / \Delta' \right)[2]|^2 \cdot C_{LP}(\overline{\mathrm{rd}}(\Gamma)) \\&\overset{\quad\,\,\,\,\,}{\leq} C_{H1R}(2\overline{\mathrm{rd}}(\Gamma)) \cdot | \left( {\mathbf{H}}(\mathbb{F}_p) / {\mathbf{H}}(\mathbb{F}_p)' \right)[2]|^2 \cdot C_{LP}(\overline{\mathrm{rd}}(\Gamma)) \\&\overset{\quad\,\,\,\,\,}{\leq} C_{H1R}(2\overline{\mathrm{rd}}(\Gamma)) \cdot | \left( {\mathbf{H}}(\mathbb{F}_p) / {\mathbf{H}}'(\mathbb{F}_p) \right)[2]|^2 \cdot [ {\mathbf{H}}'(\mathbb{F}_p) : {\mathbf{H}}(\mathbb{F}_p)' ]^2\cdot C_{LP}(\overline{\mathrm{rd}}(\Gamma)) \\&\overset{{3.1.6}}{\leq} C_{H1R}(2\overline{\mathrm{rd}}(\Gamma)) \cdot | \left( ({\mathbf{H}}/{\mathbf{H}}')(\mathbb{F}_p)\right)[2]|^2 \cdot 2^{4\overline{\mathrm{rd}}(\Gamma)}\cdot C_{LP}(\overline{\mathrm{rd}}(\Gamma)) \\&\overset{\quad\,\,\,\,\,}{\leq} C_{H1R}(2\overline{\mathrm{rd}}(\Gamma)) \cdot 2^{8\overline{\mathrm{rd}}(\Gamma)}\cdot C_{LP}(\overline{\mathrm{rd}}(\Gamma))=C_{H1}(\overline{\mathrm{rd}}(\Gamma)). \\[-39pt]\end{align*} $$
$$ \begin{align*} |H^1(S_2,\Gamma)| &\overset{{6.0.3}}{\leq} |H^1(S_2,\Gamma/\operatorname{\mathrm{Rad}}_p(\Gamma))| \cdot \max_{\tau} |H^1_\tau(S_2,\operatorname{\mathrm{Rad}}_p(\Gamma))|\overset{{5.0.2} }{=} |H^1(S_2,\Gamma/\operatorname{\mathrm{Rad}}_p(\Gamma))| \\&\overset{{6.0.3}}{\leq} \max_{\tau}|H^1_\tau(S_2,\Delta)| \cdot |H^1(S_2,(\Gamma/(\operatorname{\mathrm{Rad}}_p(\Gamma))/\Delta))| \\&\overset{{6.0.3}}{\leq} \max_{\tau} |H^1_{\tau}(S_2,\Delta)| \cdot [\Gamma/\operatorname{\mathrm{Rad}}_p(\Gamma):\Delta] \\&\overset{\quad\,\,\,\,\,}{\leq} \max_{\tau}|H^1_\tau(S_2,\Delta)| C_{LP}(\overline{\mathrm{rd}}(\Gamma)) \\& \overset{{6.0.3}}{\leq} \max_{\sigma} |H^1_\sigma(S_2,\Delta')| \cdot \max_{\tau} |H^1_\tau(S_2,\Delta / \Delta')| \cdot C_{LP}(\overline{\mathrm{rd}}(\Gamma)) \\& \overset{{6.0.2}}{\leq} \max_{\sigma} |H^1_\sigma(S_2,{\mathbf{H}}(\mathbb{F}_p)')| \cdot | \left( \Delta / \Delta' \right)[2]|^2 \cdot C_{LP}(\overline{\mathrm{rd}}(\Gamma)) \\& \overset{{6.0.4}}{\leq} C_{H1R}(2\overline{\mathrm{rd}}(\Gamma)) \cdot | \left( \Delta / \Delta' \right)[2]|^2 \cdot C_{LP}(\overline{\mathrm{rd}}(\Gamma)) \\&\overset{\quad\,\,\,\,\,}{\leq} C_{H1R}(2\overline{\mathrm{rd}}(\Gamma)) \cdot | \left( {\mathbf{H}}(\mathbb{F}_p) / {\mathbf{H}}(\mathbb{F}_p)' \right)[2]|^2 \cdot C_{LP}(\overline{\mathrm{rd}}(\Gamma)) \\&\overset{\quad\,\,\,\,\,}{\leq} C_{H1R}(2\overline{\mathrm{rd}}(\Gamma)) \cdot | \left( {\mathbf{H}}(\mathbb{F}_p) / {\mathbf{H}}'(\mathbb{F}_p) \right)[2]|^2 \cdot [ {\mathbf{H}}'(\mathbb{F}_p) : {\mathbf{H}}(\mathbb{F}_p)' ]^2\cdot C_{LP}(\overline{\mathrm{rd}}(\Gamma)) \\&\overset{{3.1.6}}{\leq} C_{H1R}(2\overline{\mathrm{rd}}(\Gamma)) \cdot | \left( ({\mathbf{H}}/{\mathbf{H}}')(\mathbb{F}_p)\right)[2]|^2 \cdot 2^{4\overline{\mathrm{rd}}(\Gamma)}\cdot C_{LP}(\overline{\mathrm{rd}}(\Gamma)) \\&\overset{\quad\,\,\,\,\,}{\leq} C_{H1R}(2\overline{\mathrm{rd}}(\Gamma)) \cdot 2^{8\overline{\mathrm{rd}}(\Gamma)}\cdot C_{LP}(\overline{\mathrm{rd}}(\Gamma))=C_{H1}(\overline{\mathrm{rd}}(\Gamma)). \\[-39pt]\end{align*} $$
Corollary 6.0.6. There is an increasing function
![]() $ C^{her}_{H1}:\mathbb N\to \mathbb N$
such that, for any pair of finite groups
$ C^{her}_{H1}:\mathbb N\to \mathbb N$
such that, for any pair of finite groups
![]() $\Delta \subset \Gamma $
, any involution
$\Delta \subset \Gamma $
, any involution
![]() $\theta $
of
$\theta $
of
![]() $\Delta $
and any prime
$\Delta $
and any prime
![]() $p>2$
,
$p>2$
,
Proof. Define
By Corollary 4.1.2, there is a
![]() $\theta $
-invariant normal subgroup
$\theta $
-invariant normal subgroup
![]() $\Delta ^\circ \lhd \Delta $
such that
$\Delta ^\circ \lhd \Delta $
such that
![]() $\overline {\mathrm {rd}}_p(\Delta ^\circ )\leq \overline {\mathrm {rd}}_p(\Gamma )$
and
$\overline {\mathrm {rd}}_p(\Delta ^\circ )\leq \overline {\mathrm {rd}}_p(\Gamma )$
and
![]() $[\Delta :\Delta ^\circ ]\leq C_{mon}(\overline {\mathrm {rd}}_p(\Gamma ))$
. The previous proposition (Proposition 6.0.5) implies that
$[\Delta :\Delta ^\circ ]\leq C_{mon}(\overline {\mathrm {rd}}_p(\Gamma ))$
. The previous proposition (Proposition 6.0.5) implies that
![]() $|H^1(S_2,\Delta ^\circ )|< C_{H1}(\overline {\mathrm {rd}}_p(\Gamma )).$
From the exact sequence
$|H^1(S_2,\Delta ^\circ )|< C_{H1}(\overline {\mathrm {rd}}_p(\Gamma )).$
From the exact sequence
we get
 $$ \begin{align*} |H^1(S_2,\Delta)| &\leq |H^1(S_2,\Delta^\circ)|\cdot |H^1(S_2,\Delta/\Delta^\circ)| \\&\leq C_{H1}(\overline{\mathrm{rd}}_p(\Gamma)) [\Delta:\Delta^\circ] \\&\leq C_{H1}(\overline{\mathrm{rd}}_p(\Gamma)) C_{mon}(\overline{\mathrm{rd}}_p(\Gamma)) \\&= C^{her}_{H1}(\overline{\mathrm{rd}}_p(\Gamma)).\\[-39pt] \end{align*} $$
$$ \begin{align*} |H^1(S_2,\Delta)| &\leq |H^1(S_2,\Delta^\circ)|\cdot |H^1(S_2,\Delta/\Delta^\circ)| \\&\leq C_{H1}(\overline{\mathrm{rd}}_p(\Gamma)) [\Delta:\Delta^\circ] \\&\leq C_{H1}(\overline{\mathrm{rd}}_p(\Gamma)) C_{mon}(\overline{\mathrm{rd}}_p(\Gamma)) \\&= C^{her}_{H1}(\overline{\mathrm{rd}}_p(\Gamma)).\\[-39pt] \end{align*} $$
7 Bounds on
 $H^2(\Gamma ,\mu _{p^\infty })$
$H^2(\Gamma ,\mu _{p^\infty })$
Let ![]() denote the group of roots of unity of order which is a power of p. In this section, we prove that
denote the group of roots of unity of order which is a power of p. In this section, we prove that ![]() is trivial whenever
is trivial whenever
![]() $\operatorname {\mathrm {Rad}}_p(\Gamma )=1$
and p is large with respect to
$\operatorname {\mathrm {Rad}}_p(\Gamma )=1$
and p is large with respect to
![]() $\mathrm {rd}_p(\Gamma )$
. See Proposition 7.0.2 below.
$\mathrm {rd}_p(\Gamma )$
. See Proposition 7.0.2 below.
We will need the following:
Lemma 7.0.1. For any short exact sequence of finite groups
we have
-
1. If
 $p \nmid | \Gamma _1 |$
, then
$p \nmid | \Gamma _1 |$
, then
 $H^i(\Gamma _2,\mathbb {F}_p)\cong H^i(\Gamma _3,\mathbb {F}_p)$
, for all i.
$H^i(\Gamma _2,\mathbb {F}_p)\cong H^i(\Gamma _3,\mathbb {F}_p)$
, for all i. -
2. If
 $p \nmid | \Gamma _3 |$
, then
$p \nmid | \Gamma _3 |$
, then
 $H^i(\Gamma _2,\mathbb {F}_p)\cong H^i(\Gamma _1,\mathbb {F}_p)^{\Gamma _3}$
, for all i.
$H^i(\Gamma _2,\mathbb {F}_p)\cong H^i(\Gamma _1,\mathbb {F}_p)^{\Gamma _3}$
, for all i.
Proof. For a pair finite group
![]() $\Gamma \lhd \Gamma '$
, let
$\Gamma \lhd \Gamma '$
, let
![]() $I^{\Gamma '}_{\Gamma }:{\mathcal M}_{\mathbb {F}_p}(\Gamma ') \to {\mathcal M}(\Gamma '/\Gamma )$
be the functor of
$I^{\Gamma '}_{\Gamma }:{\mathcal M}_{\mathbb {F}_p}(\Gamma ') \to {\mathcal M}(\Gamma '/\Gamma )$
be the functor of
![]() $\Gamma $
-invariants from the category of
$\Gamma $
-invariants from the category of
![]() $\mathbb {F}_p$
-representations of
$\mathbb {F}_p$
-representations of
![]() $\Gamma '$
to the category of
$\Gamma '$
to the category of
![]() $\mathbb {F}_p$
-representations of
$\mathbb {F}_p$
-representations of
![]() $\Gamma '/\Gamma $
. Note that, if
$\Gamma '/\Gamma $
. Note that, if
![]() $p \nmid |\Gamma |$
, then
$p \nmid |\Gamma |$
, then
![]() $I^{\Gamma '}_{\Gamma }$
is exact. Also denote
$I^{\Gamma '}_{\Gamma }$
is exact. Also denote
Now
-
1. If
 $p \nmid | \Gamma _1 |$
, then
$p \nmid | \Gamma _1 |$
, then  $$ \begin{align*} H^i(\Gamma_2,\mathbb{F}_p) & \cong R^i(I_{\Gamma_2})(\mathbb{F}_p) \cong R^i(I^{}_{\Gamma_3} \circ I^{\Gamma_2}_{\Gamma_1})(F_p) \cong R^i(I^{}_{\Gamma_3}) \circ I^{\Gamma_2}_{\Gamma_1} (\mathbb{F}_p) \cong \\&\cong R^i(I^{}_{\Gamma_3}) (\mathbb{F}_p) \cong H^i(\Gamma_3,\mathbb{F}_p). \end{align*} $$
$$ \begin{align*} H^i(\Gamma_2,\mathbb{F}_p) & \cong R^i(I_{\Gamma_2})(\mathbb{F}_p) \cong R^i(I^{}_{\Gamma_3} \circ I^{\Gamma_2}_{\Gamma_1})(F_p) \cong R^i(I^{}_{\Gamma_3}) \circ I^{\Gamma_2}_{\Gamma_1} (\mathbb{F}_p) \cong \\&\cong R^i(I^{}_{\Gamma_3}) (\mathbb{F}_p) \cong H^i(\Gamma_3,\mathbb{F}_p). \end{align*} $$
-
2. If
 $p\nmid | \Gamma _3 |$
, then
$p\nmid | \Gamma _3 |$
, then  $$ \begin{align*}H^i(\Gamma_2,\mathbb{F}_p)&\cong R^i(I_{\Gamma_2})(\mathbb{F}_p)\cong R^i(I^{}_{\Gamma_3} \circ I^{\Gamma_2}_{\Gamma_1})(F_p)\\&\cong I^{}_{\Gamma_3} \circ R^i I^{\Gamma_2}_{\Gamma_1} (\mathbb{F}_p) \cong I^{}_{\Gamma_3} (H^i(\Gamma_1,\mathbb{F}_p)) \cong H^i(\Gamma_1,\mathbb{F}_p)^{\Gamma_3}.\\[-38pt] \end{align*} $$
$$ \begin{align*}H^i(\Gamma_2,\mathbb{F}_p)&\cong R^i(I_{\Gamma_2})(\mathbb{F}_p)\cong R^i(I^{}_{\Gamma_3} \circ I^{\Gamma_2}_{\Gamma_1})(F_p)\\&\cong I^{}_{\Gamma_3} \circ R^i I^{\Gamma_2}_{\Gamma_1} (\mathbb{F}_p) \cong I^{}_{\Gamma_3} (H^i(\Gamma_1,\mathbb{F}_p)) \cong H^i(\Gamma_1,\mathbb{F}_p)^{\Gamma_3}.\\[-38pt] \end{align*} $$
Now we can prove the main result of this section:
Proposition 7.0.2 (vanishing of
 $H^2$
for large p).
$H^2$
for large p).
There is an increasing function
![]() $C_{H2}:\mathbb N\to \mathbb N$
such that for any
$C_{H2}:\mathbb N\to \mathbb N$
such that for any
-
1. integer n,
-
2. prime
 $p>C_{H2}(n)$
,
$p>C_{H2}(n)$
, -
3. finite group
 $\Gamma $
such that
$\Gamma $
such that
 $\operatorname {\mathrm {Rad}}_p(\Gamma )=1$
and
$\operatorname {\mathrm {Rad}}_p(\Gamma )=1$
and
 $\mathrm {rd}_p(\Gamma )\leq n$
,
$\mathrm {rd}_p(\Gamma )\leq n$
,
the group ![]() is trivial.
is trivial.
Proof. It is enough to show the claim after replacing ![]() by
by
![]() $\mathbb {F}_p$
. Define
$\mathbb {F}_p$
. Define
Fix n. Let
![]() $p>C_{H2}(n)$
be a prime and
$p>C_{H2}(n)$
be a prime and
![]() $\Gamma $
be a finite group such that
$\Gamma $
be a finite group such that
![]() $\operatorname {\mathrm {Rad}}_p(\Gamma )=1$
, and
$\operatorname {\mathrm {Rad}}_p(\Gamma )=1$
, and
![]() $\mathrm {rd}_p(\Gamma )\leq n$
. We have to show that
$\mathrm {rd}_p(\Gamma )\leq n$
. We have to show that
By Corollary 4.0.13 applied with trivial involution,Footnote
1
there are a normal subgroup
![]() $\Delta \lhd \Gamma $
, a connected reductive algebraic group
$\Delta \lhd \Gamma $
, a connected reductive algebraic group
![]() ${\mathbf {H}}$
defined over
${\mathbf {H}}$
defined over
![]() $\mathbb {F}_p$
and an injective homomorphism
$\mathbb {F}_p$
and an injective homomorphism
![]() $\rho : \Delta \rightarrow {\mathbf {H}}(\mathbb {F}_p)$
such that
$\rho : \Delta \rightarrow {\mathbf {H}}(\mathbb {F}_p)$
such that
-
1.
 $[\Gamma :\Delta ] \leq {C_{LP}}(n)$
.
$[\Gamma :\Delta ] \leq {C_{LP}}(n)$
. -
2.
 ${\mathbf {H}}(\mathbb {F}_p)'< \rho (\Delta ) < {\mathbf {H}}(\mathbb {F}_p)$
.
${\mathbf {H}}(\mathbb {F}_p)'< \rho (\Delta ) < {\mathbf {H}}(\mathbb {F}_p)$
. -
3.
 ${\operatorname {dim}} {\mathbf {H}}\leq 2n$
.
${\operatorname {dim}} {\mathbf {H}}\leq 2n$
.
Applying 7.0.1(2) to the embedding
![]() $\Delta \subset \Gamma $
, it is enough to prove that
$\Delta \subset \Gamma $
, it is enough to prove that
![]() $H^2(\Delta ,\mathbb {F}_p)=0$
. We will identify
$H^2(\Delta ,\mathbb {F}_p)=0$
. We will identify
![]() $\rho (\Delta )$
with
$\rho (\Delta )$
with
![]() $\Delta $
.
$\Delta $
.
Let
![]() $\Delta _0=\Delta \cap {\mathbf {H}}'(\mathbb {F}_p)$
. We have an embedding of
$\Delta _0=\Delta \cap {\mathbf {H}}'(\mathbb {F}_p)$
. We have an embedding of
![]() $\Delta /\Delta _0$
into
$\Delta /\Delta _0$
into
![]() $({\mathbf {H}}/{\mathbf {H}}')(\mathbb {F}_p)$
. Thus,
$({\mathbf {H}}/{\mathbf {H}}')(\mathbb {F}_p)$
. Thus,
![]() $p \nmid [\Delta ,\Delta _0]$
. By descent of
$p \nmid [\Delta ,\Delta _0]$
. By descent of
![]() $H^2$
to a subgroup (Lemma 7.0.1(2)), this implies that it is enough to show that
$H^2$
to a subgroup (Lemma 7.0.1(2)), this implies that it is enough to show that
By Lemma 3.1.6,
![]() $[\Delta _0:{\mathbf {H}}'(\mathbb {F}_p)'] \leq 4^n$
. By Lemma 7.0.1(2), it is enough to show that
$[\Delta _0:{\mathbf {H}}'(\mathbb {F}_p)'] \leq 4^n$
. By Lemma 7.0.1(2), it is enough to show that
![]() $H^2({\mathbf {H}}'(\mathbb {F}_p)',\mathbb {F}_p)=0$
.
$H^2({\mathbf {H}}'(\mathbb {F}_p)',\mathbb {F}_p)=0$
.
Let
![]() $\pi : \widetilde {{\mathbf {H}}'} \to {\mathbf {H}}'$
the universal cover. By Corollary 3.1.3,
$\pi : \widetilde {{\mathbf {H}}'} \to {\mathbf {H}}'$
the universal cover. By Corollary 3.1.3,
and the latter group vanishes by combining descent of
![]() $H^2$
to a quotient (Lemma 7.0.1(1)) and vanishing of
$H^2$
to a quotient (Lemma 7.0.1(1)) and vanishing of
![]() $H^2$
for simply connected groups (Theorem 3.1.1(2)).
$H^2$
for simply connected groups (Theorem 3.1.1(2)).
8 The case of trivial p-radical
In this section, we prove a twisted version of the main result of the paper for the special case when
![]() $\Gamma $
has a trivial p-radical (see Corollary 8.0.5 below).
$\Gamma $
has a trivial p-radical (see Corollary 8.0.5 below).
We start with the case that
![]() $\Gamma $
is a finite group of Lie type. This case, in the larger generality of spherical pairs but without a twist, was proved in [Reference ShechterShe]. A variation of the argument of [Reference ShechterShe] proves the twisted case. We include this variation in Appendix A. In particular, the following is a special case of Theorem 1.0.1:
$\Gamma $
is a finite group of Lie type. This case, in the larger generality of spherical pairs but without a twist, was proved in [Reference ShechterShe]. A variation of the argument of [Reference ShechterShe] proves the twisted case. We include this variation in Appendix A. In particular, the following is a special case of Theorem 1.0.1:
Theorem 8.0.1. There is an increasing function
![]() $C_{rd}:\mathbb N\to \mathbb N$
such that, for every finite field F of characteristic
$C_{rd}:\mathbb N\to \mathbb N$
such that, for every finite field F of characteristic
![]() $>3$
, every connected reductive group
$>3$
, every connected reductive group
![]() ${\mathbf {G}}$
and every involution t of
${\mathbf {G}}$
and every involution t of
![]() ${\mathbf {G}}$
, we have
${\mathbf {G}}$
, we have
In order to apply this theorem to arbitrary groups with trivial p-radical, we will need the following:
Lemma 8.0.2 (cf. [Reference Aizenbud and AvniAA19, Lemma 3.2.1]).
Let
![]() $\phi :\Gamma _1\to \Gamma _2$
be morphism finite groups and let
$\phi :\Gamma _1\to \Gamma _2$
be morphism finite groups and let
![]() $\theta _1,\theta _2$
be involutions of
$\theta _1,\theta _2$
be involutions of
![]() $\Gamma _1,\Gamma _2$
such that
$\Gamma _1,\Gamma _2$
such that
![]() $\theta _2\circ \phi =\phi \circ \theta _1$
. Then,
$\theta _2\circ \phi =\phi \circ \theta _1$
. Then,
-
1.
 $\mu (\Gamma _2,\theta _2) \leq [\Gamma _2 : \phi (\Gamma _1)] \mu (\Gamma _1,\theta _1).$
$\mu (\Gamma _2,\theta _2) \leq [\Gamma _2 : \phi (\Gamma _1)] \mu (\Gamma _1,\theta _1).$
-
2.
 $\nu (\Gamma _2,\theta _2) \leq [\Gamma _2 : \phi (\Gamma _1)] \nu (\Gamma _1,\theta _1).$
$\nu (\Gamma _2,\theta _2) \leq [\Gamma _2 : \phi (\Gamma _1)] \nu (\Gamma _1,\theta _1).$
Lemma 8.0.3. For every prime p and every connected reductive group
![]() ${\mathbf {H}}$
over
${\mathbf {H}}$
over
![]() $\mathbb {F}_p$
, we have
$\mathbb {F}_p$
, we have
![]() $\left[ {\mathbf {H}}(\mathbb {F}_p) : {\mathbf {H}}(\mathbb {F}_p)' \cdot Z({\mathbf {H}})(\mathbb {F}_p) \right] \leq 2^{2{\operatorname {dim}}\, {\mathbf {H}}}$
.
$\left[ {\mathbf {H}}(\mathbb {F}_p) : {\mathbf {H}}(\mathbb {F}_p)' \cdot Z({\mathbf {H}})(\mathbb {F}_p) \right] \leq 2^{2{\operatorname {dim}}\, {\mathbf {H}}}$
.
Proof. The map
![]() $\phi : {\mathbf {H}}' \times Z({\mathbf {H}}) \rightarrow {\mathbf {H}}$
is an isogeny. By Lemma 3.1.5 and Theorem 3.1.1,
$\phi : {\mathbf {H}}' \times Z({\mathbf {H}}) \rightarrow {\mathbf {H}}$
is an isogeny. By Lemma 3.1.5 and Theorem 3.1.1,
where
![]() $\widetilde {{\mathbf {H}}'}$
is the universal cover of
$\widetilde {{\mathbf {H}}'}$
is the universal cover of
![]() ${\mathbf {H}}'$
. By Lemma 3.1.6,
${\mathbf {H}}'$
. By Lemma 3.1.6,
![]() $[{\mathbf {H}}'(\mathbb {F}_p):{\mathbf {H}}(\mathbb {F}_p)'] \leq 2^{{\operatorname {dim}}\, {\mathbf {H}}'}$
, and the result follows.
$[{\mathbf {H}}'(\mathbb {F}_p):{\mathbf {H}}(\mathbb {F}_p)'] \leq 2^{{\operatorname {dim}}\, {\mathbf {H}}'}$
, and the result follows.
The following lemma is straightforward.
Lemma 8.0.4. If
![]() $A,B$
are finite groups and
$A,B$
are finite groups and
![]() $\theta _A,\theta _B$
are involutions of
$\theta _A,\theta _B$
are involutions of
![]() $A,B$
, then
$A,B$
, then
![]() $\mu (A \times B, \theta _A \times \theta _B)=\mu (A,\theta _A)\mu (B,\theta _B)$
.
$\mu (A \times B, \theta _A \times \theta _B)=\mu (A,\theta _A)\mu (B,\theta _B)$
.
Corollary 8.0.5. There is an increasing function
![]() $C_{nr}: \mathbb {N} \rightarrow \mathbb {N}$
such that, for any prime
$C_{nr}: \mathbb {N} \rightarrow \mathbb {N}$
such that, for any prime
![]() $p>3$
and any finite group
$p>3$
and any finite group
![]() $\Gamma $
that has a trivial p-radical, we have
$\Gamma $
that has a trivial p-radical, we have
![]() $\mu (\Gamma )<C_{nr}(\mathrm {rd}(\Gamma ))$
.
$\mu (\Gamma )<C_{nr}(\mathrm {rd}(\Gamma ))$
.
Proof. Set
Let
![]() $\theta $
be an involution of
$\theta $
be an involution of
![]() $\Gamma $
. Applying Corollary 4.0.13 to
$\Gamma $
. Applying Corollary 4.0.13 to
![]() $\Gamma $
, we get a triple
$\Gamma $
, we get a triple
![]() $\Delta ,{\mathbf {H}},t$
. By Lemma 8.0.2, we have
$\Delta ,{\mathbf {H}},t$
. By Lemma 8.0.2, we have
Denote
![]() $S={\mathbf {H}}(\mathbb {F}_p)'$
and
$S={\mathbf {H}}(\mathbb {F}_p)'$
and
![]() $Z=Z({\mathbf {H}})(\mathbb {F}_p)$
. Note that S and Z are t-invariant subgroups of
$Z=Z({\mathbf {H}})(\mathbb {F}_p)$
. Note that S and Z are t-invariant subgroups of
![]() ${\mathbf {H}}(\mathbb {F}_p)$
. By Lemma 8.0.3,
${\mathbf {H}}(\mathbb {F}_p)$
. By Lemma 8.0.3,
Let
![]() $\varphi :S \times Z \rightarrow H(\mathbb {F}_p)$
be the multiplication map.
$\varphi :S \times Z \rightarrow H(\mathbb {F}_p)$
be the multiplication map.
![]() $\varphi $
is equivariant if we use the involution
$\varphi $
is equivariant if we use the involution
![]() $\theta \times \theta $
on
$\theta \times \theta $
on
![]() $S \times Z$
. By Lemma 8.0.2(1),
$S \times Z$
. By Lemma 8.0.2(1),
Since
![]() $S \subset \Delta $
, we get that
$S \subset \Delta $
, we get that
![]() $\varphi ^{-1} (\Delta )=S \times A$
, for some
$\varphi ^{-1} (\Delta )=S \times A$
, for some
![]() $A \subset Z$
. Therefore, by Lemma 8.0.4,
$A \subset Z$
. Therefore, by Lemma 8.0.4,
Finally, by Lemma 3.1.6,
and the result follows from Theorem 8.0.1.
9 Clifford theory
We recall the elements of Clifford theory. The following lemma is standard.
Lemma 9.0.1. Let
![]() $\Gamma $
be a finite group, let
$\Gamma $
be a finite group, let
![]() $\rho $
be an irreducible representation of
$\rho $
be an irreducible representation of
![]() $\Gamma $
and let
$\Gamma $
and let
![]() $N \lhd \Gamma $
be a normal subgroup of
$N \lhd \Gamma $
be a normal subgroup of
![]() $\Gamma $
. Let
$\Gamma $
. Let
![]() $\tau $
be an irreducible subrepresentation of
$\tau $
be an irreducible subrepresentation of
![]() $\rho \restriction _N$
and let
$\rho \restriction _N$
and let
![]() $\sigma $
be the
$\sigma $
be the
![]() $\tau $
-isotypic component of
$\tau $
-isotypic component of
![]() $\rho \restriction _N$
. Let
$\rho \restriction _N$
. Let
![]() $\Delta :=\Gamma _\tau $
be the stabilizer of
$\Delta :=\Gamma _\tau $
be the stabilizer of
![]() $\tau \in \operatorname {Irr}(N)$
with respect to the adjoint action. Then
$\tau \in \operatorname {Irr}(N)$
with respect to the adjoint action. Then
![]() $\sigma $
is
$\sigma $
is
![]() $\Delta $
-invariant and
$\Delta $
-invariant and
Lemma 9.0.2. Let
![]() $\Gamma $
be a finite group, let
$\Gamma $
be a finite group, let
![]() $\rho $
be an irreducible representation of
$\rho $
be an irreducible representation of
![]() $\Gamma $
and let
$\Gamma $
and let
![]() $N \lhd \Gamma $
be a normal p-subgroup of
$N \lhd \Gamma $
be a normal p-subgroup of
![]() $\Gamma $
, and
$\Gamma $
, and
![]() $\rho \in \operatorname {Irr}(\Gamma )$
. Assume that
$\rho \in \operatorname {Irr}(\Gamma )$
. Assume that
![]() $\rho \restriction _N$
is isotypic and that
$\rho \restriction _N$
is isotypic and that ![]() is trivial.
is trivial.
Then there exist
![]() $\pi _1,\pi _2\in \operatorname {Irr}(\Gamma )$
such that
$\pi _1,\pi _2\in \operatorname {Irr}(\Gamma )$
such that
![]() $\pi _1\restriction _N$
is irreducible, the action of N on
$\pi _1\restriction _N$
is irreducible, the action of N on
![]() $\pi _2$
is trivial, and
$\pi _2$
is trivial, and
![]() $\rho \simeq \pi _1\otimes \pi _2$
.
$\rho \simeq \pi _1\otimes \pi _2$
.
Proof. Write
![]() $\rho \restriction _N= \tau ^{\oplus C}$
, where
$\rho \restriction _N= \tau ^{\oplus C}$
, where
![]() $(\tau ,V) \in Irr(N)$
. Recall the construction of the 2-cocycle corresponding to the triple
$(\tau ,V) \in Irr(N)$
. Recall the construction of the 2-cocycle corresponding to the triple
![]() $(\Gamma ,N,\tau )$
: choose a set of coset representatives
$(\Gamma ,N,\tau )$
: choose a set of coset representatives
![]() $T \subset \Gamma $
such that
$T \subset \Gamma $
such that
![]() $1\in T$
. For every
$1\in T$
. For every
![]() $t\in T\smallsetminus \left\{ 1 \right\}$
, choose an isomorphism
$t\in T\smallsetminus \left\{ 1 \right\}$
, choose an isomorphism
![]() $A_t: \tau ^t \rightarrow \tau $
such that
$A_t: \tau ^t \rightarrow \tau $
such that
![]() $\det (A_t)=1$
, and let
$\det (A_t)=1$
, and let
![]() $A_1=I$
.
$A_1=I$
.
Define a map
![]() $\pi :\Gamma \to \operatorname {\mathrm {End}}_{\mathbb C}(V)$
by
$\pi :\Gamma \to \operatorname {\mathrm {End}}_{\mathbb C}(V)$
by
![]() $\pi (tn)=A_t \tau (n)$
for
$\pi (tn)=A_t \tau (n)$
for
![]() $t\in T$
and
$t\in T$
and
![]() $n\in N$
. This is a projective representation of
$n\in N$
. This is a projective representation of
![]() $\Gamma $
that extands
$\Gamma $
that extands
![]() $\tau $
and satisfies
$\tau $
and satisfies
![]() $\pi (tn)=\pi (t) \pi (n)$
and
$\pi (tn)=\pi (t) \pi (n)$
and
For every
![]() $\gamma _1,\gamma _2\in \Gamma $
, the map
$\gamma _1,\gamma _2\in \Gamma $
, the map
is an intertwiner of
![]() $\tau $
, so
$\tau $
, so
for some
![]() $\alpha (\gamma _1,\gamma _2)\in \mathbb {C} ^ \times $
. The map
$\alpha (\gamma _1,\gamma _2)\in \mathbb {C} ^ \times $
. The map
![]() $\alpha :\Gamma \times \Gamma \to \mathbb C^\times $
is a 2-cocycle of
$\alpha :\Gamma \times \Gamma \to \mathbb C^\times $
is a 2-cocycle of
![]() $\Gamma $
with coefficients in
$\Gamma $
with coefficients in
![]() $\mathbb {C} ^ \times $
, and a simple computation shows that
$\mathbb {C} ^ \times $
, and a simple computation shows that
![]() $\alpha $
descends to a 2-cocycle on
$\alpha $
descends to a 2-cocycle on
![]() $\Gamma / N$
. Since N is a p-group,
$\Gamma / N$
. Since N is a p-group, ![]() , for every
, for every
![]() $n\in N$
. Since
$n\in N$
. Since
![]() $\det (A_t)=1$
, for every
$\det (A_t)=1$
, for every
![]() $t\in T$
, we get that
$t\in T$
, we get that ![]() . Since
. Since
![]() ${\operatorname {dim}}\, \tau $
is a p-th power, we get that
${\operatorname {dim}}\, \tau $
is a p-th power, we get that ![]() .
.
By assumption, this implies that
![]() $\alpha $
is cohomologous to the trivial cocycle, and, therefore, there is a representation
$\alpha $
is cohomologous to the trivial cocycle, and, therefore, there is a representation
![]() $\tau _1$
of
$\tau _1$
of
![]() $\Gamma $
such that
$\Gamma $
such that
![]() $\tau _1\restriction _{N}=\tau $
. Since
$\tau _1\restriction _{N}=\tau $
. Since
![]() $\tau $
is irreducible, so is
$\tau $
is irreducible, so is
![]() $\tau _1$
. By [Reference IsaacsIsa06, Corollary 6.17],
$\tau _1$
. By [Reference IsaacsIsa06, Corollary 6.17],
![]() $\rho =\tau _1 \otimes \tau _2$
, for some
$\rho =\tau _1 \otimes \tau _2$
, for some
![]() $\tau _2\in \operatorname {\mathrm {Irr}}(\Gamma / N)$
.
$\tau _2\in \operatorname {\mathrm {Irr}}(\Gamma / N)$
.
10 Proof of the main theorem
In this section, we prove Theorem c and deduce Theorem A and Corollary B.
Lemma 10.0.1 the main theorem for product case.
Let
![]() $C_{nr}$
be the increasing function given by Corollary 8.0.5. Then, for every
$C_{nr}$
be the increasing function given by Corollary 8.0.5. Then, for every
-
• prime
 $p>2$
,
$p>2$
, -
• symmetric pair of finite groups
 $(\Gamma ,\Gamma ^\theta )$
,
$(\Gamma ,\Gamma ^\theta )$
, -
•
 $\rho _1 \in \operatorname {Irr}(\Gamma )$
such that
$\rho _1 \in \operatorname {Irr}(\Gamma )$
such that
 ${\rho _1}|_{\operatorname {\mathrm {Rad}}_p(\Gamma )}$
is irreducible,
${\rho _1}|_{\operatorname {\mathrm {Rad}}_p(\Gamma )}$
is irreducible, -
•
 $\rho _2 \in \operatorname {Irr}(\Gamma )$
that factors through
$\rho _2 \in \operatorname {Irr}(\Gamma )$
that factors through
 $\Gamma /\operatorname {\mathrm {Rad}}_p(\Gamma )$
,
$\Gamma /\operatorname {\mathrm {Rad}}_p(\Gamma )$
,
we have
Proof. Since odd order symmetric pairs are Gelfand pairs (Corollary 5.0.5(1)), we have
If
![]() $(\rho _1\otimes \rho _2)^{\Gamma ^\theta }=0$
, the claim trivially holds. Otherwise, let
$(\rho _1\otimes \rho _2)^{\Gamma ^\theta }=0$
, the claim trivially holds. Otherwise, let
![]() $\chi $
be the character with which
$\chi $
be the character with which
![]() $\Gamma ^\theta /Rad_p(\Gamma )^\theta $
acts on
$\Gamma ^\theta /Rad_p(\Gamma )^\theta $
acts on
![]() $\rho _1^{Rad_p(\Gamma )^\theta }$
. Using Corollary 8.0.5,
$\rho _1^{Rad_p(\Gamma )^\theta }$
. Using Corollary 8.0.5,
Using Clifford theory, the last lemma implies the following:
Corollary 10.0.2. There is an increasing function
![]() $C_{\nu '}:\mathbb N\to \mathbb N$
such that, for every prime
$C_{\nu '}:\mathbb N\to \mathbb N$
such that, for every prime
![]() $p>2$
and any finite group
$p>2$
and any finite group
![]() $\Gamma $
, we have
$\Gamma $
, we have
where
![]() $\nu ^{\prime }_p$
is the function defined in Notations 2.2.4.
$\nu ^{\prime }_p$
is the function defined in Notations 2.2.4.
Proof. Define
![]() $C_{\nu '}(n)=\max ((C_{H2}(n)+1)^{n},C_{nr}(n))$
. We will prove the corollary by analyzing two cases:
$C_{\nu '}(n)=\max ((C_{H2}(n)+1)^{n},C_{nr}(n))$
. We will prove the corollary by analyzing two cases:
-
Case 1.
 $p\leq C_{H2}(\overline {\mathrm {rd}}(\Gamma ))$
.
$p\leq C_{H2}(\overline {\mathrm {rd}}(\Gamma ))$
.In this case,
 $$ \begin{align*}|\Gamma/Rad_p(\Gamma)|\leq (p+1)^{\overline{\mathrm{rd}}(\Gamma)}\leq (C_{H2}(\overline{\mathrm{rd}}(\Gamma))+1)^{\overline{\mathrm{rd}}(\Gamma)}\leq C_{\nu'}(\overline{\mathrm{rd}}(\Gamma)).\end{align*} $$
$$ \begin{align*}|\Gamma/Rad_p(\Gamma)|\leq (p+1)^{\overline{\mathrm{rd}}(\Gamma)}\leq (C_{H2}(\overline{\mathrm{rd}}(\Gamma))+1)^{\overline{\mathrm{rd}}(\Gamma)}\leq C_{\nu'}(\overline{\mathrm{rd}}(\Gamma)).\end{align*} $$
Since we can control multiplicities when we pass to subgroup of bounded index (Lemma 8.0.2), we get that
 $$ \begin{align*}\nu(\Gamma)\leq |\Gamma/Rad_p(\Gamma)| \cdot \nu(Rad_p(\Gamma)).\end{align*} $$
$$ \begin{align*}\nu(\Gamma)\leq |\Gamma/Rad_p(\Gamma)| \cdot \nu(Rad_p(\Gamma)).\end{align*} $$
Since odd order symmetric pairs are Gelfand pairs (Corollary 5.0.5(1)), we have that
 $$ \begin{align*}\nu(Rad_p(\Gamma))=1.\end{align*} $$
$$ \begin{align*}\nu(Rad_p(\Gamma))=1.\end{align*} $$
We obtain
 $$ \begin{align*}\nu^{\prime}_p(\Gamma)\leq \nu(\Gamma)\leq \#(\Gamma/Rad_p(\Gamma)) \leq C_{\nu'}(\overline{\mathrm{rd}}(\Gamma))\end{align*} $$
$$ \begin{align*}\nu^{\prime}_p(\Gamma)\leq \nu(\Gamma)\leq \#(\Gamma/Rad_p(\Gamma)) \leq C_{\nu'}(\overline{\mathrm{rd}}(\Gamma))\end{align*} $$
-
Case 2.
 $p> C_{H2}(\overline {\mathrm {rd}}(\Gamma ))$
.
$p> C_{H2}(\overline {\mathrm {rd}}(\Gamma ))$
.By Proposition 7.0.2, the group
 is trivial. Let
is trivial. Let
 $\rho \in \operatorname {Irr}(\Gamma )$
be such that
$\rho \in \operatorname {Irr}(\Gamma )$
be such that
 $\rho |_{Rad_p(\Gamma )}$
is isotypic. By Clifford theory (Lemma 9.0.2), there exist
$\rho |_{Rad_p(\Gamma )}$
is isotypic. By Clifford theory (Lemma 9.0.2), there exist
 $\pi _1,\pi _2\in \operatorname {Irr}(\Gamma )$
such that
$\pi _1,\pi _2\in \operatorname {Irr}(\Gamma )$
such that
 $\pi _1|_{Rad_p(\Gamma )}$
is irreducible, the action of
$\pi _1|_{Rad_p(\Gamma )}$
is irreducible, the action of
 $Rad_p(\Gamma )$
on
$Rad_p(\Gamma )$
on
 $\pi _2$
is trivial and
$\pi _2$
is trivial and
 $\rho \simeq \pi _1\otimes \pi _2$
. Thus, the main theorem for product case (Lemma 10.0.1) implies that, for any involution
$\rho \simeq \pi _1\otimes \pi _2$
. Thus, the main theorem for product case (Lemma 10.0.1) implies that, for any involution
 $\theta $
of
$\theta $
of
 $\Gamma $
, we have
$\Gamma $
, we have  $$ \begin{align*}\rho^{\Gamma^\theta}= (\pi_1\otimes \pi_2)^{\Gamma^\theta}\leq C_{nr}(\overline{\mathrm{rd}}(\Gamma))\leq C_{\nu'}(\overline{\mathrm{rd}}(\Gamma)).\\[-40pt]\end{align*} $$
$$ \begin{align*}\rho^{\Gamma^\theta}= (\pi_1\otimes \pi_2)^{\Gamma^\theta}\leq C_{nr}(\overline{\mathrm{rd}}(\Gamma))\leq C_{\nu'}(\overline{\mathrm{rd}}(\Gamma)).\\[-40pt]\end{align*} $$
We are now ready to prove the main theorem:
Proof of Theorem 2.3.1.
Define C recursively by
-
1.
 $C(0):=1$
$C(0):=1$
-
2.
 $C(n):=C^{her}_{H1}(n)\max (C_{\nu '}(n),C(n-1)C_{mon}(n))$
,
$C(n):=C^{her}_{H1}(n)\max (C_{\nu '}(n),C(n-1)C_{mon}(n))$
,
where
![]() $C^{her}_{H1}$
is given by Corollary 6.0.6,
$C^{her}_{H1}$
is given by Corollary 6.0.6,
![]() $C_{\nu '}$
is given by Corollary 10.0.2 and
$C_{\nu '}$
is given by Corollary 10.0.2 and
![]() $C_{mon}$
is given by Corollary 4.1.2. We will prove the theorem by induction. We assume the theorem holds if
$C_{mon}$
is given by Corollary 4.1.2. We will prove the theorem by induction. We assume the theorem holds if
![]() $\overline {\mathrm {rd}}_p(\Gamma )<n$
and prove it in the case
$\overline {\mathrm {rd}}_p(\Gamma )<n$
and prove it in the case
![]() $\overline {\mathrm {rd}}(\Gamma )=n$
.
$\overline {\mathrm {rd}}(\Gamma )=n$
.
Let
![]() $\theta $
be an involution of
$\theta $
be an involution of
![]() $\Gamma $
and
$\Gamma $
and
![]() $\rho \in \operatorname {\mathrm {Irr}} \Gamma $
. Let
$\rho \in \operatorname {\mathrm {Irr}} \Gamma $
. Let
![]() $N:=Rad_p(\Gamma )$
. If
$N:=Rad_p(\Gamma )$
. If
![]() $(\rho |_N)^{N^\theta }=0$
, we are done. Otherwise, let
$(\rho |_N)^{N^\theta }=0$
, we are done. Otherwise, let
![]() $\tau $
be an irreducible direct summand of
$\tau $
be an irreducible direct summand of
![]() $\rho |_N$
such that
$\rho |_N$
such that
![]() $(\tau )^{N^\theta }\neq 0$
. By the Lapid–Prasad property for symmetric pairs of odd order (Corollary 5.0.5(2)), we have
$(\tau )^{N^\theta }\neq 0$
. By the Lapid–Prasad property for symmetric pairs of odd order (Corollary 5.0.5(2)), we have
![]() $(\tau )^{\theta }\cong \tau ^*$
. Let
$(\tau )^{\theta }\cong \tau ^*$
. Let
![]() $\Delta :=\Gamma _\tau $
. We have
$\Delta :=\Gamma _\tau $
. We have
showing that
![]() $\Delta $
is
$\Delta $
is
![]() $\theta $
-stable.
$\theta $
-stable.
By Clifford theory (Lemma 9.0.1), we have
where
![]() $\sigma \in \operatorname {Irr}(\Delta )$
is such that
$\sigma \in \operatorname {Irr}(\Delta )$
is such that
![]() $\sigma |_N$
is
$\sigma |_N$
is
![]() $\tau $
-isotypic. Therefore,
$\tau $
-isotypic. Therefore,
where
 $$ \begin{align*} &\Gamma^{dis} = \{g\in \Gamma| \sigma^{\Delta\cap (\Gamma^\theta)^g} \neq 0\} \subset \{g\in \Gamma| \sigma^{N\cap (\Gamma^\theta)^g} \neq 0\} = \{g\in \Gamma| \tau^{N\cap (\Gamma^\theta)^g} \neq 0\}=\\ &=\{g\in \Gamma| (\tau^g)^{N\cap (\Gamma^\theta)} \neq 0\}=\{g\in \Gamma| (\tau^g)^{N^\theta} \neq 0\}\subset \{g\in \Gamma| (\tau^g)^* \circ \theta \simeq \tau^g\} =:\Gamma^{inv}. \end{align*} $$
$$ \begin{align*} &\Gamma^{dis} = \{g\in \Gamma| \sigma^{\Delta\cap (\Gamma^\theta)^g} \neq 0\} \subset \{g\in \Gamma| \sigma^{N\cap (\Gamma^\theta)^g} \neq 0\} = \{g\in \Gamma| \tau^{N\cap (\Gamma^\theta)^g} \neq 0\}=\\ &=\{g\in \Gamma| (\tau^g)^{N\cap (\Gamma^\theta)} \neq 0\}=\{g\in \Gamma| (\tau^g)^{N^\theta} \neq 0\}\subset \{g\in \Gamma| (\tau^g)^* \circ \theta \simeq \tau^g\} =:\Gamma^{inv}. \end{align*} $$
The last inclution is by the Lapid-Prasad property for symmetric pairs of odd order (Corollary 5.0.5(2)).
We analyze the quotient
![]() $\Delta \backslash \Gamma ^{inv}/\Gamma ^\theta $
. Since
$\Delta \backslash \Gamma ^{inv}/\Gamma ^\theta $
. Since
![]() $(\tau ^g)^* \circ \theta =(\tau ^*\circ \theta )^{\theta (g)}=\tau ^{\theta (g)}$
, we have
$(\tau ^g)^* \circ \theta =(\tau ^*\circ \theta )^{\theta (g)}=\tau ^{\theta (g)}$
, we have
Thus, for any
![]() $g\in \Gamma ^{inv}$
, we have
$g\in \Gamma ^{inv}$
, we have
and hence,
![]() $ad(g^{-1})(\Delta )$
is
$ad(g^{-1})(\Delta )$
is
![]() $\theta $
-stable.
$\theta $
-stable.
We also have
and thus,
Combining the last equality with (2), we get
 $$ \begin{align*} {\operatorname{dim}} \rho^{\Gamma^\theta}&\leq |H^1(S_2,\Delta)| \max_{g\in \Gamma^{inv}} {\operatorname{dim}} \sigma^{\Delta \cap (\Gamma^{\theta})^g} \\& = |H^1(S_2,\Delta)| \max\limits_{g\in \Gamma^{inv}} {\operatorname{dim}} (\sigma\circ ad(g))^{(ad(g^{-1})(\Delta)) \cap \Gamma^\theta} \\& = |H^1(S_2,\Delta)| \max\limits_{g\in \Gamma^{inv}} {\operatorname{dim}} (\sigma\circ ad(g))^{(ad(g^{-1})(\Delta))^\theta} \\& = |H^1(S_2,\Delta)| \max\limits_{g\in \Gamma^{inv}} {\operatorname{dim}} \sigma^{\Delta^{ad(g)\circ\theta\circ ad(g^{-1})}} \\& \leq |H^1(S_2,\Delta)|\max\limits_{\theta' \text{ is an involution of } \Delta} ({\operatorname{dim}} (\sigma^{\Delta^{\theta'}})). \end{align*} $$
$$ \begin{align*} {\operatorname{dim}} \rho^{\Gamma^\theta}&\leq |H^1(S_2,\Delta)| \max_{g\in \Gamma^{inv}} {\operatorname{dim}} \sigma^{\Delta \cap (\Gamma^{\theta})^g} \\& = |H^1(S_2,\Delta)| \max\limits_{g\in \Gamma^{inv}} {\operatorname{dim}} (\sigma\circ ad(g))^{(ad(g^{-1})(\Delta)) \cap \Gamma^\theta} \\& = |H^1(S_2,\Delta)| \max\limits_{g\in \Gamma^{inv}} {\operatorname{dim}} (\sigma\circ ad(g))^{(ad(g^{-1})(\Delta))^\theta} \\& = |H^1(S_2,\Delta)| \max\limits_{g\in \Gamma^{inv}} {\operatorname{dim}} \sigma^{\Delta^{ad(g)\circ\theta\circ ad(g^{-1})}} \\& \leq |H^1(S_2,\Delta)|\max\limits_{\theta' \text{ is an involution of } \Delta} ({\operatorname{dim}} (\sigma^{\Delta^{\theta'}})). \end{align*} $$
By our bound on
![]() $H^1(S_2,\Delta )$
(Corollary 6.0.6),
$H^1(S_2,\Delta )$
(Corollary 6.0.6),
We finish the proof by analyzing the following cases:
-
Case 1.
 $\operatorname {\mathrm {Rad}}_p(\Gamma )\neq \operatorname {\mathrm {Rad}}_p(\Delta )$
:
$\operatorname {\mathrm {Rad}}_p(\Gamma )\neq \operatorname {\mathrm {Rad}}_p(\Delta )$
:In order to bound
 $\nu (\Delta )$
, we fix an involution
$\nu (\Delta )$
, we fix an involution
 $\theta '$
of
$\theta '$
of
 $\Delta $
. By Corollary 4.1.2, we can find a
$\Delta $
. By Corollary 4.1.2, we can find a
 $\theta '$
-invariant subgroup
$\theta '$
-invariant subgroup
 $\Delta ^\circ \lhd \Delta $
such that
$\Delta ^\circ \lhd \Delta $
such that  $$ \begin{align*}\overline{\mathrm{rd}}_p(\Delta^\circ)<\overline{\mathrm{rd}}_p(\Gamma)\end{align*} $$
$$ \begin{align*}\overline{\mathrm{rd}}_p(\Delta^\circ)<\overline{\mathrm{rd}}_p(\Gamma)\end{align*} $$
and
 $$ \begin{align*}[\Delta:\Delta^\circ] \leq C_{mon}(\overline{\mathrm{rd}}_p(\Gamma)).\end{align*} $$
$$ \begin{align*}[\Delta:\Delta^\circ] \leq C_{mon}(\overline{\mathrm{rd}}_p(\Gamma)).\end{align*} $$
The induction assumption implies that
 $\nu (\Delta ^\circ )\leq C(\overline {\mathrm {rd}}_p(\Gamma )-1)$
. Lemma 8.0.2(2) implies that
$\nu (\Delta ^\circ )\leq C(\overline {\mathrm {rd}}_p(\Gamma )-1)$
. Lemma 8.0.2(2) implies that  $$ \begin{align*} \nu(\Delta,\theta')&\leq [\Delta:\Delta^\circ]\cdot \nu(\Delta^\circ,\theta'|_{\Delta^\circ}) \leq C_{mon}(\overline{\mathrm{rd}}_p(\Gamma)) C(\overline{\mathrm{rd}}_p(\Gamma)-1), \end{align*} $$
$$ \begin{align*} \nu(\Delta,\theta')&\leq [\Delta:\Delta^\circ]\cdot \nu(\Delta^\circ,\theta'|_{\Delta^\circ}) \leq C_{mon}(\overline{\mathrm{rd}}_p(\Gamma)) C(\overline{\mathrm{rd}}_p(\Gamma)-1), \end{align*} $$
so
 $$ \begin{align*}\nu(\Delta) \leq C_{mon}(\overline{\mathrm{rd}}_p(\Gamma)) C(\overline{\mathrm{rd}}_p(\Gamma)-1).\end{align*} $$
$$ \begin{align*}\nu(\Delta) \leq C_{mon}(\overline{\mathrm{rd}}_p(\Gamma)) C(\overline{\mathrm{rd}}_p(\Gamma)-1).\end{align*} $$
It follows that
as required. $$ \begin{align*} {\operatorname{dim}} \rho^{\Gamma^\theta}\leq C_{H1}^{her}(\overline{\mathrm{rd}}_p(\Gamma ))\cdot C_{mon}(\overline{\mathrm{rd}}_p(\Gamma)) C(\overline{\mathrm{rd}}_p(\Gamma)-1)\leq C(\overline{\mathrm{rd}}_p(\Gamma )),\end{align*} $$
$$ \begin{align*} {\operatorname{dim}} \rho^{\Gamma^\theta}\leq C_{H1}^{her}(\overline{\mathrm{rd}}_p(\Gamma ))\cdot C_{mon}(\overline{\mathrm{rd}}_p(\Gamma)) C(\overline{\mathrm{rd}}_p(\Gamma)-1)\leq C(\overline{\mathrm{rd}}_p(\Gamma )),\end{align*} $$
-
Case 2.
 $\operatorname {\mathrm {Rad}}_p(\Gamma )= \operatorname {\mathrm {Rad}}_p(\Delta )$
.
$\operatorname {\mathrm {Rad}}_p(\Gamma )= \operatorname {\mathrm {Rad}}_p(\Delta )$
.In this case,
 $\overline {\mathrm {rd}}_p(\Delta )\leq \overline {\mathrm {rd}}_p(\Gamma )$
, and
$\overline {\mathrm {rd}}_p(\Delta )\leq \overline {\mathrm {rd}}_p(\Gamma )$
, and
 $\sigma |_{\operatorname {\mathrm {Rad}}_p(\Delta )}$
is isotypic. By (3) and Corollary 10.0.2,
$\sigma |_{\operatorname {\mathrm {Rad}}_p(\Delta )}$
is isotypic. By (3) and Corollary 10.0.2,  $$ \begin{align*} {\operatorname{dim}} \rho^{\Gamma^\theta}&\leq C^{her}_{H1}(\overline{\mathrm{rd}}_p(\Gamma))\cdot \nu'(\Delta) \\&\leq C^{her}_{H1}(\overline{\mathrm{rd}}_p(\Gamma)) C_{\nu'}(\overline{\mathrm{rd}}_p(\Delta)) \\&\leq C^{her}_{H1}(\overline{\mathrm{rd}}_p(\Gamma)) C_{\nu'}(\overline{\mathrm{rd}}_p(\Gamma))\leq C(\overline{\mathrm{rd}}_p(\Gamma)).\\[-37pt] \end{align*} $$
$$ \begin{align*} {\operatorname{dim}} \rho^{\Gamma^\theta}&\leq C^{her}_{H1}(\overline{\mathrm{rd}}_p(\Gamma))\cdot \nu'(\Delta) \\&\leq C^{her}_{H1}(\overline{\mathrm{rd}}_p(\Gamma)) C_{\nu'}(\overline{\mathrm{rd}}_p(\Delta)) \\&\leq C^{her}_{H1}(\overline{\mathrm{rd}}_p(\Gamma)) C_{\nu'}(\overline{\mathrm{rd}}_p(\Gamma))\leq C(\overline{\mathrm{rd}}_p(\Gamma)).\\[-37pt] \end{align*} $$
10.1 Deduction of Theorem A, Corollary B and Corollary D
We will now deduce Theorem A from our main result, first reminding its formulation.
Theorem A. There is an increasing function
![]() $C^{\mathit{fin}}:\mathbb N\to \mathbb N$
such that, for any
$C^{\mathit{fin}}:\mathbb N\to \mathbb N$
such that, for any
-
• odd prime p,
-
• positive integer d,
-
• finite group
 $\Gamma $
,
$\Gamma $
, -
• normal p-subgroup
 $N\lhd \Gamma $
,
$N\lhd \Gamma $
, -
• an embedding
 $\Gamma /N \hookrightarrow GL_d(\mathbb {F}_p)$
,
$\Gamma /N \hookrightarrow GL_d(\mathbb {F}_p)$
, -
• an involution
 $\theta $
of
$\theta $
of
 $\Gamma $
,
$\Gamma $
, -
• an irreducible representation
 $\rho $
of
$\rho $
of
 $\Gamma $
,
$\Gamma $
,
we have
![]() ${\operatorname {dim}} \rho ^{ \Gamma ^\theta } \leq C^{\mathit{fin}}(d)$
.
${\operatorname {dim}} \rho ^{ \Gamma ^\theta } \leq C^{\mathit{fin}}(d)$
.
Proof. Set
By Corollary 4.1.2, we have a subgroup
![]() $\Delta \lhd \Gamma /N$
such that
$\Delta \lhd \Gamma /N$
such that
and
Let
![]() $\Gamma ^\circ $
be the preimage of
$\Gamma ^\circ $
be the preimage of
![]() $\Delta $
under the projection
$\Delta $
under the projection
![]() $\Gamma \to \Gamma /N$
. We have
$\Gamma \to \Gamma /N$
. We have
By the main theorem (Theorem 2.3.1),
Lemma 8.0.2(2) implies that
Proof of Corollary B.
Set
![]() $\Lambda =C^{\mathit{fin}}(C^{lin}(d))$
, where
$\Lambda =C^{\mathit{fin}}(C^{lin}(d))$
, where
![]() $C^{lin}$
is the function given by Lemma 3.2.2.
$C^{lin}$
is the function given by Lemma 3.2.2.
Let
![]() $\psi :{\mathbf {G}} \rightarrow \mathbf {R}$
be the reductive quotient of
$\psi :{\mathbf {G}} \rightarrow \mathbf {R}$
be the reductive quotient of
![]() ${\mathbf {G}}$
and let
${\mathbf {G}}$
and let
![]() $\varphi : \mathbf {R}\to GL_{{{C^{lin}}}(d),F}$
be the embedding given by Lemma 3.2.2. The group
$\varphi : \mathbf {R}\to GL_{{{C^{lin}}}(d),F}$
be the embedding given by Lemma 3.2.2. The group
![]() $\varphi \circ \psi (K)$
is a compact subgroup of
$\varphi \circ \psi (K)$
is a compact subgroup of
![]() $GL_{{{C^{lin}}}(d)}(F)$
and, after conjugation, we may assume that
$GL_{{{C^{lin}}}(d)}(F)$
and, after conjugation, we may assume that
![]() $\varphi \circ \psi (K)\subset GL_{{{C^{lin}}}(d)}(O_F)$
. Let
$\varphi \circ \psi (K)\subset GL_{{{C^{lin}}}(d)}(O_F)$
. Let
![]() $K_1\subset GL_{{{C^{lin}}}(d)}(O_F)$
be the first congruence subgroup.
$K_1\subset GL_{{{C^{lin}}}(d)}(O_F)$
be the first congruence subgroup.
Set
![]() $M:=K\cap (\varphi \circ \psi )^{-1}(K_1)$
,
$M:=K\cap (\varphi \circ \psi )^{-1}(K_1)$
,
![]() $L:=M\cap \ker \rho $
, and
$L:=M\cap \ker \rho $
, and
![]() $P:=L \cap \theta (L)$
. The claim now follows by applying Theorem A to
$P:=L \cap \theta (L)$
. The claim now follows by applying Theorem A to
![]() $\Gamma := K/P$
,
$\Gamma := K/P$
,
![]() $N:=M/P$
, and the embedding
$N:=M/P$
, and the embedding
![]() $\Gamma / N = K/M \hookrightarrow \operatorname {\mathrm {GL}}_{{{C^{lin}}}(d)}(O_F)/K_1=\operatorname {\mathrm {GL}}_{{{C^{lin}}}(d)}(\mathbb {F}_p)$
.
$\Gamma / N = K/M \hookrightarrow \operatorname {\mathrm {GL}}_{{{C^{lin}}}(d)}(O_F)/K_1=\operatorname {\mathrm {GL}}_{{{C^{lin}}}(d)}(\mathbb {F}_p)$
.
Proof of Corollary D.
There is a constant
![]() $C=C({\mathbf {G}},\theta )$
such that, for every prime p, the number of connected components of
$C=C({\mathbf {G}},\theta )$
such that, for every prime p, the number of connected components of
![]() ${\mathbf {G}}^ \theta \times \operatorname {\mathrm {Spec}}(\overline {\mathbb {F}_p})$
is at most C. We claim that, for every p, the set
${\mathbf {G}}^ \theta \times \operatorname {\mathrm {Spec}}(\overline {\mathbb {F}_p})$
is at most C. We claim that, for every p, the set
![]() $\mathbf {X}(\mathbb {Z}_p)$
is a union of at most
$\mathbf {X}(\mathbb {Z}_p)$
is a union of at most
![]() $C\ {\mathbf {G}}(\mathbb {Z}_p)$
-orbits. Corollary D follows from
$C\ {\mathbf {G}}(\mathbb {Z}_p)$
-orbits. Corollary D follows from
-
• The claim.
-
• The fact that each
 ${\mathbf {G}}(\mathbb {Z}_p)$
-orbit has the form
${\mathbf {G}}(\mathbb {Z}_p)$
-orbit has the form
 ${\mathbf {G}}(\mathbb {Z}_p)/{\mathbf {G}}(\mathbb {Z}_p)^{\theta _i}$
, for some involutions
${\mathbf {G}}(\mathbb {Z}_p)/{\mathbf {G}}(\mathbb {Z}_p)^{\theta _i}$
, for some involutions
 $\theta _i$
of
$\theta _i$
of
 ${\mathbf {G}}(\mathbb {Z}_p)$
.
${\mathbf {G}}(\mathbb {Z}_p)$
. -
•
 ${\operatorname {dim}} {\operatorname {Hom}} \left( \rho ,C^\infty ({\mathbf {G}}(O)/{\mathbf {G}}(O)^{\theta _i})\right) = {\operatorname {dim}} \rho ^{{\mathbf {G}}(O)^{\theta _i}}$
.
${\operatorname {dim}} {\operatorname {Hom}} \left( \rho ,C^\infty ({\mathbf {G}}(O)/{\mathbf {G}}(O)^{\theta _i})\right) = {\operatorname {dim}} \rho ^{{\mathbf {G}}(O)^{\theta _i}}$
. -
• Corollary B.
It remains to prove the claim. For this, it is enough to show that, for every prime p and every natural number n, the number of
![]() ${\mathbf {G}}(\mathbb {Z}/p^n)$
-orbits in
${\mathbf {G}}(\mathbb {Z}/p^n)$
-orbits in
![]() $\mathbf {X}(\mathbb {Z}/p^n)$
is bounded by C. Recall that the Greenberg functor is a functor from the category of
$\mathbf {X}(\mathbb {Z}/p^n)$
is bounded by C. Recall that the Greenberg functor is a functor from the category of
![]() $\mathbb {Z} /p^n$
-schemes to the category of
$\mathbb {Z} /p^n$
-schemes to the category of
![]() $\mathbb {F}_p$
-schemes that satisfies that
$\mathbb {F}_p$
-schemes that satisfies that
![]() $Gr_n(X)(\mathbb {F}_p)=X(\mathbb {Z} /p^n)$
. There is a natural transformation
$Gr_n(X)(\mathbb {F}_p)=X(\mathbb {Z} /p^n)$
. There is a natural transformation
![]() $Gr_n(X) \rightarrow X \times \operatorname {\mathrm {Spec}}(\mathbb {F}_p)$
. For the definition of the Greenberg functor, see, for example, [Reference Bosch, Lütkebohmert and RaynaudBLR90, pp. 276].
$Gr_n(X) \rightarrow X \times \operatorname {\mathrm {Spec}}(\mathbb {F}_p)$
. For the definition of the Greenberg functor, see, for example, [Reference Bosch, Lütkebohmert and RaynaudBLR90, pp. 276].
From the long exact sequence of Galois cohomologies of
![]() $\operatorname {\mathrm {Gal}}(\overline {\mathbb {F}_p}/\mathbb {F}_p)$
with coefficients in
$\operatorname {\mathrm {Gal}}(\overline {\mathbb {F}_p}/\mathbb {F}_p)$
with coefficients in
![]() $Gr_n({\mathbf {G}}^ \theta )$
,
$Gr_n({\mathbf {G}}^ \theta )$
,
![]() $Gr_n({\mathbf {G}})$
and
$Gr_n({\mathbf {G}})$
and
![]() $Gr_n(\mathbf {X})$
(see, for example, [Reference SerreSer02, §5.4, Corollary 1]), the orbit space of
$Gr_n(\mathbf {X})$
(see, for example, [Reference SerreSer02, §5.4, Corollary 1]), the orbit space of
![]() $Gr_n(\mathbf {X})(\mathbb {F}_p)=\mathbf {X}(\mathbb {Z} /p^n)$
under
$Gr_n(\mathbf {X})(\mathbb {F}_p)=\mathbf {X}(\mathbb {Z} /p^n)$
under
![]() $Gr_n({\mathbf {G}})(\mathbb {F}_p)={\mathbf {G}}(\mathbb {Z} / p^n)$
embeds into
$Gr_n({\mathbf {G}})(\mathbb {F}_p)={\mathbf {G}}(\mathbb {Z} / p^n)$
embeds into
![]() $H^1(\operatorname {\mathrm {Gal}}(\overline {\mathbb {F}_p}/ \mathbb {F}_p), Gr_n({\mathbf {G}}^ \theta ))$
. The kernel of
$H^1(\operatorname {\mathrm {Gal}}(\overline {\mathbb {F}_p}/ \mathbb {F}_p), Gr_n({\mathbf {G}}^ \theta ))$
. The kernel of
![]() $\pi :Gr_n({\mathbf {G}} ^ \theta ) \rightarrow {\mathbf {G}} ^ \theta \times \operatorname {\mathrm {Spec}}(\mathbb {F}_p)$
is an iterated extension of additive groups, so it is absolutely connected. By Lang’s theorem and the long exact sequence of Galois cohomologies with coefficients in
$\pi :Gr_n({\mathbf {G}} ^ \theta ) \rightarrow {\mathbf {G}} ^ \theta \times \operatorname {\mathrm {Spec}}(\mathbb {F}_p)$
is an iterated extension of additive groups, so it is absolutely connected. By Lang’s theorem and the long exact sequence of Galois cohomologies with coefficients in
![]() $\ker (\pi )$
,
$\ker (\pi )$
,
![]() $Gr_n({\mathbf {G}}^ \theta )$
and
$Gr_n({\mathbf {G}}^ \theta )$
and
![]() ${\mathbf {G}} ^ \theta \times \operatorname {\mathrm {Spec}}(\mathbb {F}_p)$
, the set
${\mathbf {G}} ^ \theta \times \operatorname {\mathrm {Spec}}(\mathbb {F}_p)$
, the set
![]() $H^1\left( \operatorname {\mathrm {Gal}}(\overline {\mathbb {F}_p}/ \mathbb {F}_p),Gr_n({\mathbf {G}}^ \theta ) \right)$
embeds into
$H^1\left( \operatorname {\mathrm {Gal}}(\overline {\mathbb {F}_p}/ \mathbb {F}_p),Gr_n({\mathbf {G}}^ \theta ) \right)$
embeds into
![]() $H^1\left( \operatorname {\mathrm {Gal}}(\overline {\mathbb {F}_p}/ \mathbb {F}_p), {\mathbf {G}}^ \theta \times \operatorname {\mathrm {Spec}}(\mathbb {F}_p) \right)$
which itself embeds into
$H^1\left( \operatorname {\mathrm {Gal}}(\overline {\mathbb {F}_p}/ \mathbb {F}_p), {\mathbf {G}}^ \theta \times \operatorname {\mathrm {Spec}}(\mathbb {F}_p) \right)$
which itself embeds into
![]() $H^1\left( \operatorname {\mathrm {Gal}}(\overline {\mathbb {F}_p}/ \mathbb {F}_p),\pi _0 \left( {\mathbf {G}}^ \theta \right)\right)$
. Since
$H^1\left( \operatorname {\mathrm {Gal}}(\overline {\mathbb {F}_p}/ \mathbb {F}_p),\pi _0 \left( {\mathbf {G}}^ \theta \right)\right)$
. Since
![]() $\operatorname {\mathrm {Gal}}(\overline {\mathbb {F}_p}/ \mathbb {F}_p)$
is pro-cyclic, a 1-cocycle is determined by its value at a topological generator, so
$\operatorname {\mathrm {Gal}}(\overline {\mathbb {F}_p}/ \mathbb {F}_p)$
is pro-cyclic, a 1-cocycle is determined by its value at a topological generator, so
![]() $H^1\left( \operatorname {\mathrm {Gal}}(\overline {\mathbb {F}_p}/ \mathbb {F}_p),\pi _0 \left( {\mathbf {G}}^ \theta \right)\right) \leq | \pi _0 \left( {\mathbf {G}}^ \theta \right) (\overline {\mathbb {F}_p}) | \leq C$
.
$H^1\left( \operatorname {\mathrm {Gal}}(\overline {\mathbb {F}_p}/ \mathbb {F}_p),\pi _0 \left( {\mathbf {G}}^ \theta \right)\right) \leq | \pi _0 \left( {\mathbf {G}}^ \theta \right) (\overline {\mathbb {F}_p}) | \leq C$
.
A Bounds on twisted multiplicities for spherical spaces of finite groups of Lie type
In this appendix, we prove the following:
Theorem A.0.1. Let
![]() ${\mathcal S}$
be a scheme of finite type, let
${\mathcal S}$
be a scheme of finite type, let
![]() ${\mathcal G} \rightarrow {\mathcal S}$
be a connected reductive group scheme of finite type over
${\mathcal G} \rightarrow {\mathcal S}$
be a connected reductive group scheme of finite type over
![]() ${\mathcal S}$
and let
${\mathcal S}$
and let
![]() ${\mathcal H} \subseteq {\mathcal G}$
be a closed (not necessarily connected) reductive subgroup scheme. Assume that, for every geometric point s of
${\mathcal H} \subseteq {\mathcal G}$
be a closed (not necessarily connected) reductive subgroup scheme. Assume that, for every geometric point s of
![]() ${\mathcal S}$
, the pair
${\mathcal S}$
, the pair
![]() $({\mathcal G}_s,{\mathcal H}_s)$
is spherical. Then there is a constant C such that, for every finite field F, any
$({\mathcal G}_s,{\mathcal H}_s)$
is spherical. Then there is a constant C such that, for every finite field F, any
![]() $s\in {\mathcal S}(F)$
, any irreducible representation
$s\in {\mathcal S}(F)$
, any irreducible representation
![]() $\rho $
of
$\rho $
of
![]() ${\mathcal G}_s(F)$
and any 1-dimensional character
${\mathcal G}_s(F)$
and any 1-dimensional character
![]() $\theta $
of
$\theta $
of
![]() ${\mathcal H}_s(F)$
,
${\mathcal H}_s(F)$
,
The proof is very similar to the one in [Reference ShechterShe]. The main additional ingredient is the geometrization of (1-dimensional) characters of finite groups of Lie type.
Given a Weil
![]() $\overline {\mathbb {Q}_\ell }$
-local system
$\overline {\mathbb {Q}_\ell }$
-local system
![]() $\mathfrak {L}$
on a scheme X over a finite field F, the sheaf to function correspondence gives a function
$\mathfrak {L}$
on a scheme X over a finite field F, the sheaf to function correspondence gives a function
![]() $X(F) \rightarrow \overline {\mathbb {Q}_\ell }$
which we denote by
$X(F) \rightarrow \overline {\mathbb {Q}_\ell }$
which we denote by
![]() $\chi _{\mathfrak {L}}$
.
$\chi _{\mathfrak {L}}$
.
Lemma A.0.2. Let
![]() ${\mathcal S}$
be a scheme of finite type and let
${\mathcal S}$
be a scheme of finite type and let
![]() ${\mathcal H} \rightarrow {\mathcal S}$
be a (not necessarily connected) reductive group scheme of finite type over
${\mathcal H} \rightarrow {\mathcal S}$
be a (not necessarily connected) reductive group scheme of finite type over
![]() ${\mathcal S}$
. There is a constant C such that, for every finite field F of size greater then
${\mathcal S}$
. There is a constant C such that, for every finite field F of size greater then
![]() $9$
, any prime
$9$
, any prime
![]() $\ell \neq char(F)$
, any
$\ell \neq char(F)$
, any
![]() $s\in {\mathcal S}(F)$
and any 1-dimensional character
$s\in {\mathcal S}(F)$
and any 1-dimensional character
![]() $\chi : {\mathcal H}_s(F) \rightarrow \overline {\mathbb {Q}_\ell }$
, there is a
$\chi : {\mathcal H}_s(F) \rightarrow \overline {\mathbb {Q}_\ell }$
, there is a
![]() $\overline {\mathbb {Q}_\ell }$
-local system
$\overline {\mathbb {Q}_\ell }$
-local system
![]() $\mathfrak {L}$
over
$\mathfrak {L}$
over
![]() ${\mathcal H}_{s}$
with a Weil structure of pure weight zero such that
${\mathcal H}_{s}$
with a Weil structure of pure weight zero such that
![]() $\chi _{\mathfrak {L}}$
is a character of a representation of
$\chi _{\mathfrak {L}}$
is a character of a representation of
![]() ${\mathcal H}_s(F)$
of dimension at most C that contains
${\mathcal H}_s(F)$
of dimension at most C that contains
![]() $\chi $
as one of its irreducible constituents.
$\chi $
as one of its irreducible constituents.
Proof. For every (not necessarily connected) reductive group
![]() ${\mathbf {G}}$
defined over a field F, let
${\mathbf {G}}$
defined over a field F, let
![]() $({\mathbf {G}}^\circ )'$
be the derived subgroup of the connected component of
$({\mathbf {G}}^\circ )'$
be the derived subgroup of the connected component of
![]() ${\mathbf {G}}$
and let
${\mathbf {G}}$
and let
![]() $\widetilde {{\mathbf {G}}}$
be the the product of the universal cover of
$\widetilde {{\mathbf {G}}}$
be the the product of the universal cover of
![]() $({\mathbf {G}}^\circ )'$
and the radical of
$({\mathbf {G}}^\circ )'$
and the radical of
![]() ${\mathbf {G}}$
. The map
${\mathbf {G}}$
. The map
![]() $\widetilde {{\mathbf {G}}}(\bar F) \rightarrow {\mathbf {G}}(\bar F)$
has finite kernel and cokernel.
$\widetilde {{\mathbf {G}}}(\bar F) \rightarrow {\mathbf {G}}(\bar F)$
has finite kernel and cokernel.
By a stratification argument, there is a constant c such that, for every field F, any
![]() $s\in {\mathcal S}(F)$
, the kernel and cokernel of the map
$s\in {\mathcal S}(F)$
, the kernel and cokernel of the map
![]() $\widetilde {{\mathcal H}_s}(\bar F) \rightarrow {\mathcal H}_s(\bar F)$
are bounded by c. By Lemma 3.1.5, if F is a finite field, the kernel and cokernel of the map
$\widetilde {{\mathcal H}_s}(\bar F) \rightarrow {\mathcal H}_s(\bar F)$
are bounded by c. By Lemma 3.1.5, if F is a finite field, the kernel and cokernel of the map
![]() $\widetilde {{\mathcal H}_s}({ F} ) \rightarrow {\mathcal H}_s({ F} )$
are bounded by
$\widetilde {{\mathcal H}_s}({ F} ) \rightarrow {\mathcal H}_s({ F} )$
are bounded by
![]() $c^2$
. We will show that the lemma holds with
$c^2$
. We will show that the lemma holds with
![]() $C=c^4$
.
$C=c^4$
.
Given
![]() $F ,\ell ,s,\chi $
as in the lemma, denote the map
$F ,\ell ,s,\chi $
as in the lemma, denote the map
![]() $\widetilde {{\mathcal H}_s} \rightarrow {\mathcal H}_s$
by
$\widetilde {{\mathcal H}_s} \rightarrow {\mathcal H}_s$
by
![]() $\varphi $
. Let
$\varphi $
. Let
![]() $R({\mathcal H}_s)$
be the radical of
$R({\mathcal H}_s)$
be the radical of
![]() ${\mathcal H}_s$
. By [Reference LusztigLus85, §5], there is a 1-dimensional local system
${\mathcal H}_s$
. By [Reference LusztigLus85, §5], there is a 1-dimensional local system
![]() $\mathcal {F}$
on
$\mathcal {F}$
on
![]() $R({\mathcal H}_s)$
such that
$R({\mathcal H}_s)$
such that
![]() $\chi _{\mathcal {F}}=\chi \restriction _{R({\mathcal H}_s)}$
.
$\chi _{\mathcal {F}}=\chi \restriction _{R({\mathcal H}_s)}$
.
By Theorem 3.1.1(3), the character
![]() $\chi \circ \varphi \restriction _{\widetilde {{\mathcal H}_s'}(F)}$
is trivial. Therefore, under the decomposition
$\chi \circ \varphi \restriction _{\widetilde {{\mathcal H}_s'}(F)}$
is trivial. Therefore, under the decomposition
![]() ${\widetilde {{\mathcal H}_s}=\widetilde {{\mathcal H}_s'}\times R({\mathcal H}_s)}$
, we have
${\widetilde {{\mathcal H}_s}=\widetilde {{\mathcal H}_s'}\times R({\mathcal H}_s)}$
, we have
where ![]() denotes the 1-dimensional trivial local system on
denotes the 1-dimensional trivial local system on
![]() $\widetilde {{\mathcal H}_s'}$
$\widetilde {{\mathcal H}_s'}$
Setting ![]() , the function
, the function
![]() $\chi _{\mathfrak {M}}$
is equal to
$\chi _{\mathfrak {M}}$
is equal to
![]() $\varphi _*(\chi \circ \varphi )$
. It follows that the restrictions of
$\varphi _*(\chi \circ \varphi )$
. It follows that the restrictions of
![]() $\chi _{\mathfrak {M}}$
and
$\chi _{\mathfrak {M}}$
and
![]() $|\ker \varphi (F)|\chi $
to
$|\ker \varphi (F)|\chi $
to
![]() $\varphi (\widetilde { {\mathcal H}_s}(F))$
coincide. Choose coset representatives
$\varphi (\widetilde { {\mathcal H}_s}(F))$
coincide. Choose coset representatives
![]() $g_1,\ldots ,g_c\in {\mathcal H}_s(F)$
to
$g_1,\ldots ,g_c\in {\mathcal H}_s(F)$
to
![]() $\varphi (\widetilde {{\mathcal H}_s}(F))$
and let
$\varphi (\widetilde {{\mathcal H}_s}(F))$
and let
![]() $\mathfrak {L} = \bigoplus \operatorname {\mathrm {Ad}}(g_i)^*(\mathfrak {M})$
. We have that
$\mathfrak {L} = \bigoplus \operatorname {\mathrm {Ad}}(g_i)^*(\mathfrak {M})$
. We have that
which implies the claim.
Now we will continue with the original argument of [Reference Aizenbud and AvniAA19, Reference ShechterShe], adapting it to include the character
![]() $\chi $
and its geometrization
$\chi $
and its geometrization
![]() $\mathfrak {L}$
.
$\mathfrak {L}$
.
Definition A.0.3. If
![]() ${\mathbf {G}}$
is an algebraic group acting on a variety
${\mathbf {G}}$
is an algebraic group acting on a variety
![]() $\mathbf {X}$
, we let
$\mathbf {X}$
, we let
![]() ${{\mathbf {X}}}_{{{\mathbf {G}}}} =\left\{ (x,g)\in X \times {{{\mathbf {G}}}} \mid g \cdot x=x \right\}$
.
${{\mathbf {X}}}_{{{\mathbf {G}}}} =\left\{ (x,g)\in X \times {{{\mathbf {G}}}} \mid g \cdot x=x \right\}$
.
Lemma A.0.4. Let
![]() ${{{\mathbf {G}}}} ,{{{\mathbf {H}}}}$
be reductive algebraic groups, let
${{{\mathbf {G}}}} ,{{{\mathbf {H}}}}$
be reductive algebraic groups, let
![]() ${{\mathbf {X}}}={{{\mathbf {G}}}} /{{{\mathbf {H}}}}$
and consider the diagram
${{\mathbf {X}}}={{{\mathbf {G}}}} /{{{\mathbf {H}}}}$
and consider the diagram

where
![]() $a(g,h)=(g{{{\mathbf {H}}}},g h g ^{-1})$
and
$a(g,h)=(g{{{\mathbf {H}}}},g h g ^{-1})$
and
![]() $p(g,h)=h$
. If
$p(g,h)=h$
. If
![]() ${{\mathfrak {L}}}$
is an
${{\mathfrak {L}}}$
is an
![]() ${\mathbf {H}}$
-equivariant local system on
${\mathbf {H}}$
-equivariant local system on
![]() ${{{\mathbf {H}}}}$
, then there is a local system
${{{\mathbf {H}}}}$
, then there is a local system
![]() ${{\mathfrak {M}}}$
on
${{\mathfrak {M}}}$
on
![]() $X_G$
such that
$X_G$
such that
![]() $a^* {{\mathfrak {M}}} \cong p^* {{\mathfrak {L}}}$
.
$a^* {{\mathfrak {M}}} \cong p^* {{\mathfrak {L}}}$
.
Proof. We construct
![]() $\mathfrak {M}$
using descent. The main point is that
$\mathfrak {M}$
using descent. The main point is that
![]() $({{{\mathbf {G}}}} \times {{{\mathbf {H}}}}) \times _{{{\mathbf {X}}}_{{{\mathbf {G}}}}} ({{{\mathbf {G}}}} \times {{{\mathbf {H}}}})\cong {{{\mathbf {G}}}} \times {{{\mathbf {H}}}} \times {{{\mathbf {H}}}}$
via the map
$({{{\mathbf {G}}}} \times {{{\mathbf {H}}}}) \times _{{{\mathbf {X}}}_{{{\mathbf {G}}}}} ({{{\mathbf {G}}}} \times {{{\mathbf {H}}}})\cong {{{\mathbf {G}}}} \times {{{\mathbf {H}}}} \times {{{\mathbf {H}}}}$
via the map
![]() $((g_1,h_1),(g_2,h_2)) \mapsto (g_1,g_2 ^{-1} g_1,h_1)$
. We get a diagram
$((g_1,h_1),(g_2,h_2)) \mapsto (g_1,g_2 ^{-1} g_1,h_1)$
. We get a diagram

where
![]() $a_1,a_2,p_1,p_2$
are the projections,
$a_1,a_2,p_1,p_2$
are the projections,
![]() $b_1(x,y)=x$
and
$b_1(x,y)=x$
and
![]() $b_2(x,y)=x y x ^{-1}$
. We have
$b_2(x,y)=x y x ^{-1}$
. We have
![]() $b_ip_2=p_1a_i$
for
$b_ip_2=p_1a_i$
for
![]() $i=1,2$
. The equivariance of
$i=1,2$
. The equivariance of
![]() ${{\mathfrak {L}}}$
gives an identification
${{\mathfrak {L}}}$
gives an identification
![]() $\alpha : b_1^* {{\mathfrak {L}}} \rightarrow b_2^* {{\mathfrak {L}}}$
, which gives an identification
$\alpha : b_1^* {{\mathfrak {L}}} \rightarrow b_2^* {{\mathfrak {L}}}$
, which gives an identification
![]() $\beta :a_1^* p_1^* {{\mathfrak {L}}} = (b_1p_2)^*{{\mathfrak {L}}} \rightarrow (b_2p_2)^* {{\mathfrak {L}}} = a_2^* p_1^* {{\mathfrak {L}}}$
, and it is easy to check that
$\beta :a_1^* p_1^* {{\mathfrak {L}}} = (b_1p_2)^*{{\mathfrak {L}}} \rightarrow (b_2p_2)^* {{\mathfrak {L}}} = a_2^* p_1^* {{\mathfrak {L}}}$
, and it is easy to check that
![]() $\beta $
satisfies the cocycle identity. By descent,
$\beta $
satisfies the cocycle identity. By descent,
![]() $p_1^* {{\mathfrak {L}}}$
is the pullback of a sheaf
$p_1^* {{\mathfrak {L}}}$
is the pullback of a sheaf
![]() ${{\mathfrak {M}}}$
on
${{\mathfrak {M}}}$
on
![]() ${{\mathbf {X}}}_{{{\mathbf {G}}}}$
. Since a is onto, we get that
${{\mathbf {X}}}_{{{\mathbf {G}}}}$
. Since a is onto, we get that
![]() ${{\mathfrak {M}}}$
is a local system.
${{\mathfrak {M}}}$
is a local system.
In the next lemma, we use the notion of induced character sheaf; see [Reference Aizenbud and AvniAA19, Definition 2.2.1].
Lemma A.0.5. Let
![]() ${{{\mathcal S}}}$
be a scheme of finite type, let
${{{\mathcal S}}}$
be a scheme of finite type, let
![]() ${{{\mathcal G}}} \rightarrow {{{\mathcal S}}}$
be a connected reductive group scheme of finite type over
${{{\mathcal G}}} \rightarrow {{{\mathcal S}}}$
be a connected reductive group scheme of finite type over
![]() ${{{\mathcal S}}}$
and let
${{{\mathcal S}}}$
and let
![]() ${{{\mathcal H}}} \subseteq {{{\mathcal G}}}$
be a closed (not necessarily connected) reductive subgroup scheme. Assume that, for every geometric point s of
${{{\mathcal H}}} \subseteq {{{\mathcal G}}}$
be a closed (not necessarily connected) reductive subgroup scheme. Assume that, for every geometric point s of
![]() ${{{\mathcal S}}}$
, the pair
${{{\mathcal S}}}$
, the pair
![]() $({{{\mathcal G}}}_s,{{{\mathcal H}}}_s)$
is spherical. There is a constant
$({{{\mathcal G}}}_s,{{{\mathcal H}}}_s)$
is spherical. There is a constant
![]() $C_1$
such that, for any finite field
$C_1$
such that, for any finite field
![]() ${{F}} $
, any
${{F}} $
, any
![]() $s\in {{{\mathcal S}}}({{F}} )$
, any induced character sheaf
$s\in {{{\mathcal S}}}({{F}} )$
, any induced character sheaf
![]() ${{\mathfrak {K}}}$
on
${{\mathfrak {K}}}$
on
![]() ${{{\mathcal G}}}_s$
and any
${{{\mathcal G}}}_s$
and any
![]() ${{{\mathcal H}}}_s$
-equivariant local system
${{{\mathcal H}}}_s$
-equivariant local system
![]() ${{\mathfrak {L}}}$
on
${{\mathfrak {L}}}$
on
![]() ${{{\mathcal H}}}_s$
of weight zero,
${{{\mathcal H}}}_s$
of weight zero,
![]() ${\operatorname {dim}} {\operatorname {Hom}}_{{{{\mathcal G}}}_s({{F}} )}\left( \chi _{{{\mathfrak {K}}}},\operatorname {\mathrm {Ind}}_{{{{\mathcal H}}}_s({{F}} )}^{{{{\mathcal G}}}_s({{F}} )} \chi _{{\mathfrak {L}}} \right) < C_1 \cdot \operatorname {\mathrm {rk}} {{\mathfrak {L}}}$
.
${\operatorname {dim}} {\operatorname {Hom}}_{{{{\mathcal G}}}_s({{F}} )}\left( \chi _{{{\mathfrak {K}}}},\operatorname {\mathrm {Ind}}_{{{{\mathcal H}}}_s({{F}} )}^{{{{\mathcal G}}}_s({{F}} )} \chi _{{\mathfrak {L}}} \right) < C_1 \cdot \operatorname {\mathrm {rk}} {{\mathfrak {L}}}$
.
Proof. For every geometric point s of
![]() ${{{\mathcal S}}}$
, let
${{{\mathcal S}}}$
, let
![]() $\operatorname {\mathrm {Fl}}_s$
be the flag variety of
$\operatorname {\mathrm {Fl}}_s$
be the flag variety of
![]() ${{{\mathcal G}}}_s$
. Let
${{{\mathcal G}}}_s$
. Let
![]() $C_1$
be such that, for every geometric point s of
$C_1$
be such that, for every geometric point s of
![]() ${{{\mathcal S}}}$
, the number of connected components of
${{{\mathcal S}}}$
, the number of connected components of
![]() $({{{\mathcal G}}}_s/ {{{\mathcal H}}}_s \times \operatorname {\mathrm {Fl}}_s)_{{{{\mathcal G}}}_s}$
is bounded by
$({{{\mathcal G}}}_s/ {{{\mathcal H}}}_s \times \operatorname {\mathrm {Fl}}_s)_{{{{\mathcal G}}}_s}$
is bounded by
![]() $C_1$
.
$C_1$
.
Let
![]() ${{F}} ,s,{{\mathfrak {K}}},{{\mathfrak {L}}}$
be as in the lemma. Denote
${{F}} ,s,{{\mathfrak {K}}},{{\mathfrak {L}}}$
be as in the lemma. Denote
![]() ${{{\mathbf {G}}}}={{{\mathcal G}}}_s, {{{\mathbf {H}}}}={{{\mathcal H}}}_s,{{\mathbf {X}}}={\mathbf {G}}/{\mathbf {H}}$
and fix a Borel subgroup
${{{\mathbf {G}}}}={{{\mathcal G}}}_s, {{{\mathbf {H}}}}={{{\mathcal H}}}_s,{{\mathbf {X}}}={\mathbf {G}}/{\mathbf {H}}$
and fix a Borel subgroup
![]() $\mathbf {B}$
of
$\mathbf {B}$
of
![]() ${\mathbf {G}}$
defined over F. Consider the diagram
${\mathbf {G}}$
defined over F. Consider the diagram

where
![]() $f,\pi ,\widetilde {f},\widetilde {\pi }$
are the projections and
$f,\pi ,\widetilde {f},\widetilde {\pi }$
are the projections and
![]() $q=\pi \circ \widetilde {f}=\widetilde {\pi }\circ f$
.
$q=\pi \circ \widetilde {f}=\widetilde {\pi }\circ f$
.
By definition, there is a weight zero local system
![]() $\mathfrak {F}$
on
$\mathfrak {F}$
on
![]() $({\mathbf {G}}/\mathbf {B})_{{\mathbf {G}}}$
such that
$({\mathbf {G}}/\mathbf {B})_{{\mathbf {G}}}$
such that
![]() ${{\mathfrak {K}}}$
is a direct summand of
${{\mathfrak {K}}}$
is a direct summand of
![]() $R \pi _*\mathfrak {F}$
. Applying Lemma A.0.4 to
$R \pi _*\mathfrak {F}$
. Applying Lemma A.0.4 to
![]() ${{\mathfrak {L}}}$
, we get a local system
${{\mathfrak {L}}}$
, we get a local system
![]() ${{\mathfrak {M}}}$
on
${{\mathfrak {M}}}$
on
![]() $\mathbf {X}_{{\mathbf {G}}}$
. Since
$\mathbf {X}_{{\mathbf {G}}}$
. Since
![]() ${{\mathfrak {L}}}$
has weight zero, so does
${{\mathfrak {L}}}$
has weight zero, so does
![]() ${{\mathfrak {M}}}$
.
${{\mathfrak {M}}}$
.
By construction,
![]() $\chi _{Rf_! {{\mathfrak {M}}}}=\operatorname {\mathrm {Ind}} \chi _{{\mathfrak {L}}}$
. Denoting the standard inner product of functions on
$\chi _{Rf_! {{\mathfrak {M}}}}=\operatorname {\mathrm {Ind}} \chi _{{\mathfrak {L}}}$
. Denoting the standard inner product of functions on
![]() $G({{F}} )$
by
$G({{F}} )$
by
![]() $\langle - , - \rangle $
, we get
$\langle - , - \rangle $
, we get
 $$ \begin{align*} {\operatorname{dim}} {\operatorname{Hom}}_{{\mathbf{G}}({{F}} )} \left( \chi_{{\mathfrak{K}}} , \operatorname{\mathrm{Ind}}_{{\mathbf{H}}({{F}} )}^{{\mathbf{G}}({{F}} )} \chi_{{\mathfrak{L}}} \right) &= \left \langle \chi_{{\mathfrak{K}}} , \operatorname{\mathrm{Ind}}_{{\mathbf{H}}({{F}} )}^{{\mathbf{G}}({{F}} )} \chi_{{\mathfrak{L}}} \right \rangle \\ &= \left \langle \chi_{{{\mathfrak{K}}}}, \chi_{f_! {{\mathfrak{M}}}} \right \rangle \\ &= \left \langle \chi_{{{\mathfrak{K}}} \otimes f_! {{\mathfrak{M}}} ^\vee}, 1\right \rangle = \operatorname{\mathrm{trace}} \left( Fr_F\mid p_! {{(\mathfrak{K} \otimes f_! \mathfrak{M}^\vee)}} \right), \end{align*} $$
$$ \begin{align*} {\operatorname{dim}} {\operatorname{Hom}}_{{\mathbf{G}}({{F}} )} \left( \chi_{{\mathfrak{K}}} , \operatorname{\mathrm{Ind}}_{{\mathbf{H}}({{F}} )}^{{\mathbf{G}}({{F}} )} \chi_{{\mathfrak{L}}} \right) &= \left \langle \chi_{{\mathfrak{K}}} , \operatorname{\mathrm{Ind}}_{{\mathbf{H}}({{F}} )}^{{\mathbf{G}}({{F}} )} \chi_{{\mathfrak{L}}} \right \rangle \\ &= \left \langle \chi_{{{\mathfrak{K}}}}, \chi_{f_! {{\mathfrak{M}}}} \right \rangle \\ &= \left \langle \chi_{{{\mathfrak{K}}} \otimes f_! {{\mathfrak{M}}} ^\vee}, 1\right \rangle = \operatorname{\mathrm{trace}} \left( Fr_F\mid p_! {{(\mathfrak{K} \otimes f_! \mathfrak{M}^\vee)}} \right), \end{align*} $$
where
![]() $Fr_F$
is induced by the Frobenius map of
$Fr_F$
is induced by the Frobenius map of
![]() $\operatorname {\mathrm {Spec}}(F)$
.
$\operatorname {\mathrm {Spec}}(F)$
.
For every n, denote the degree n extension of
![]() ${{F}} $
by
${{F}} $
by
![]() ${{F}} _n$
and denote the pullbacks of
${{F}} _n$
and denote the pullbacks of
![]() ${{\mathfrak {L}}},{{\mathfrak {K}}}$
to
${{\mathfrak {L}}},{{\mathfrak {K}}}$
to
![]() ${\mathbf {G}}_{{{F}}_n},{\mathbf {H}}_{{{F}} _n}$
by
${\mathbf {G}}_{{{F}}_n},{\mathbf {H}}_{{{F}} _n}$
by
![]() ${{\mathfrak {L}}}_n,{{\mathfrak {K}}}_n$
. From the same reasoning as before, we get
${{\mathfrak {L}}}_n,{{\mathfrak {K}}}_n$
. From the same reasoning as before, we get
The complex
![]() $p_! \left( {{\mathfrak {K}}} \otimes f_! {{\mathfrak {M}}} ^\vee \right)$
is a direct summand of
$p_! \left( {{\mathfrak {K}}} \otimes f_! {{\mathfrak {M}}} ^\vee \right)$
is a direct summand of
![]() $p_! \left( \pi _! \mathfrak {F} \otimes f_! {{\mathfrak {M}}}^\vee \right)$
. Since
$p_! \left( \pi _! \mathfrak {F} \otimes f_! {{\mathfrak {M}}}^\vee \right)$
. Since
we get that
![]() $p_! \left( {{\mathfrak {K}}} \otimes f_! {{\mathfrak {M}}} ^\vee \right)$
is a direct summand of
$p_! \left( {{\mathfrak {K}}} \otimes f_! {{\mathfrak {M}}} ^\vee \right)$
is a direct summand of
![]() $p_! q_! \left( \widetilde {f}^* \mathfrak {F} \otimes \widetilde {\pi }^* {{\mathfrak {M}}}^\vee \right)$
. Since
$p_! q_! \left( \widetilde {f}^* \mathfrak {F} \otimes \widetilde {\pi }^* {{\mathfrak {M}}}^\vee \right)$
. Since
![]() $\widetilde {f}^* \mathfrak {F} \otimes \widetilde {\pi }^* {{\mathfrak {M}}}^\vee $
has weight zero, we get that the complex
$\widetilde {f}^* \mathfrak {F} \otimes \widetilde {\pi }^* {{\mathfrak {M}}}^\vee $
has weight zero, we get that the complex
![]() $p_! \left( {{\mathfrak {K}}} \otimes f_! {{\mathfrak {M}}} ^\vee \right)$
has weight zero, is concentrated in degrees
$p_! \left( {{\mathfrak {K}}} \otimes f_! {{\mathfrak {M}}} ^\vee \right)$
has weight zero, is concentrated in degrees
![]() $0,\ldots ,2{\operatorname {dim}} (\mathbf {X} \times {\mathbf {G}}/\mathbf {B})_G=2{\operatorname {dim}} {\mathbf {G}}$
and
$0,\ldots ,2{\operatorname {dim}} (\mathbf {X} \times {\mathbf {G}}/\mathbf {B})_G=2{\operatorname {dim}} {\mathbf {G}}$
and
Thus,
so, by [Reference Aizenbud and AvniAA19, Lemma 2.4.1 and the proof of Theorem 2.1.3],
Proposition A.0.6. For any d, there are integers
![]() $N,C$
such that, if
$N,C$
such that, if
-
1. F is a finite field of size greater than N,
-
2.
 ${\mathbf {G}}$
is a reductive group defined over F of dimension at most d,
${\mathbf {G}}$
is a reductive group defined over F of dimension at most d, -
3.
 $\chi $
is an irreducible character of
$\chi $
is an irreducible character of
 ${\mathbf {G}}(F)$
,
${\mathbf {G}}(F)$
,
then there are induced character sheaves
![]() $\mathfrak {K}_1,\ldots ,\mathfrak {K}_C$
and real numbers
$\mathfrak {K}_1,\ldots ,\mathfrak {K}_C$
and real numbers
![]() ${\alpha }_1,\ldots ,{\alpha }_C\in [-C,C]$
such that
${\alpha }_1,\ldots ,{\alpha }_C\in [-C,C]$
such that
![]() $\sum {\alpha }_i \chi _{\mathfrak {K}_i}-\chi $
is a non-negative combination of irreducible characters of
$\sum {\alpha }_i \chi _{\mathfrak {K}_i}-\chi $
is a non-negative combination of irreducible characters of
![]() ${\mathbf {G}}(F)$
.
${\mathbf {G}}(F)$
.
Proof. [Reference ShechterShe, Lemma A.1, Theorem 2.2, Theorem 3.3] (the last two are due to Laumon and Lusztig).
Proof of Theorem A.0.1.
Without loss of generality, we may assume that
![]() $|F|>9$
. Let
$|F|>9$
. Let
![]() $\rho $
be an irreducible representation of
$\rho $
be an irreducible representation of
![]() $G(F)$
and let
$G(F)$
and let
![]() $\theta $
be a character of
$\theta $
be a character of
![]() $H(F)$
. Let
$H(F)$
. Let
![]() $C,\mathfrak {K}_i,{\alpha }_i$
be as in Lemma A.0.6 (applied to
$C,\mathfrak {K}_i,{\alpha }_i$
be as in Lemma A.0.6 (applied to
![]() $\rho $
) and let
$\rho $
) and let
![]() $\mathfrak {L}$
be as in Lemma A.0.2 (applied to
$\mathfrak {L}$
be as in Lemma A.0.2 (applied to
![]() $\theta $
). By Lemma A.0.5, we have
$\theta $
). By Lemma A.0.5, we have
B A versal family of symmetric pairs of reductive groups over finite fields
In this appendix, we prove Lemma 3.2.2 and construct a family of symmetric pairs of reductive groups that includes all symmetric pairs of reductive groups of a given dimension over all finite fields (Lemma 3.2.1).
B.1 Proof of Lemma 3.2.2
For the proof, we will need the following:
Lemma B.1.1. There is an increasing function
![]() $C^{spt}: \mathbb {N} \rightarrow \mathbb {N}$
such that any reductive algebraic group
$C^{spt}: \mathbb {N} \rightarrow \mathbb {N}$
such that any reductive algebraic group
![]() ${\mathbf {G}}$
over an arbitrary field F splits over an extension
${\mathbf {G}}$
over an arbitrary field F splits over an extension
![]() $F'/F$
of degree at most
$F'/F$
of degree at most
![]() $C^{spt}({\operatorname {dim}}\, {\mathbf {G}})$
.
$C^{spt}({\operatorname {dim}}\, {\mathbf {G}})$
.
Proof. Set
![]() $C^{spt}(d):=3^{d^3}$
.
$C^{spt}(d):=3^{d^3}$
.
There is a maximal torus of
![]() ${\mathbf {G}}$
that is defined over F ([Reference Artin, Bertin, Demazure, Gabriel, Grothendieck, Raynaud and SerreABD+64, XIV 1.1]), so we can assume that
${\mathbf {G}}$
that is defined over F ([Reference Artin, Bertin, Demazure, Gabriel, Grothendieck, Raynaud and SerreABD+64, XIV 1.1]), so we can assume that
![]() ${\mathbf {G}}$
is a torus. Denote
${\mathbf {G}}$
is a torus. Denote
![]() $d={\operatorname {dim}}\, {\mathbf {G}}$
.
$d={\operatorname {dim}}\, {\mathbf {G}}$
.
Since
![]() ${\mathbf {G}}$
is an F-form of
${\mathbf {G}}$
is an F-form of
![]() $\mathbb {G}_m^{d}$
, we get a continuous homomorphism
$\mathbb {G}_m^{d}$
, we get a continuous homomorphism
![]() $\rho :\operatorname {\mathrm {Gal}}_F \rightarrow \operatorname {\mathrm {Aut}}(\mathbb {G}_m^{d})=\operatorname {\mathrm {GL}}_d(\mathbb {Z})$
. The image of
$\rho :\operatorname {\mathrm {Gal}}_F \rightarrow \operatorname {\mathrm {Aut}}(\mathbb {G}_m^{d})=\operatorname {\mathrm {GL}}_d(\mathbb {Z})$
. The image of
![]() $\rho $
is finite. Since the kernel of
$\rho $
is finite. Since the kernel of
![]() $\operatorname {\mathrm {GL}}_d(\mathbb {Z}) \rightarrow \operatorname {\mathrm {GL}}_d(\mathbb {Z} / 3)$
is torsion-free,
$\operatorname {\mathrm {GL}}_d(\mathbb {Z}) \rightarrow \operatorname {\mathrm {GL}}_d(\mathbb {Z} / 3)$
is torsion-free,
![]() $\rho (\operatorname {\mathrm {Gal}}_F)$
embeds in
$\rho (\operatorname {\mathrm {Gal}}_F)$
embeds in
![]() $\operatorname {\mathrm {GL}}_d(\mathbb {Z} / 3)$
, so
$\operatorname {\mathrm {GL}}_d(\mathbb {Z} / 3)$
, so
Proof of Lemma 3.2.2.
Since there are finitely many split reductive groups of given dimension, there is a function
![]() $C^{linSpt}$
such that every split reductive group
$C^{linSpt}$
such that every split reductive group
![]() ${\mathbf {H}}$
has a faithful representation of dimension
${\mathbf {H}}$
has a faithful representation of dimension
![]() $C^{linSpt}({\operatorname {dim}}\,{\mathbf {H}})$
. Given an arbitrary reductive group
$C^{linSpt}({\operatorname {dim}}\,{\mathbf {H}})$
. Given an arbitrary reductive group
![]() ${\mathbf {G}}$
, Lemma B.1.1 implies that
${\mathbf {G}}$
, Lemma B.1.1 implies that
![]() ${\mathbf {G}}$
splits over an extension
${\mathbf {G}}$
splits over an extension
![]() $F'/F$
of degree at most
$F'/F$
of degree at most
![]() $C^{spt}({\operatorname {dim}}\, {\mathbf {G}})$
. Hence, there is a faithful representation
$C^{spt}({\operatorname {dim}}\, {\mathbf {G}})$
. Hence, there is a faithful representation
![]() ${\mathbf {G}} \rightarrow \operatorname {\mathrm {Res}}_{F'/F}\operatorname {\mathrm {GL}}_{C^{linSpt}({\operatorname {dim}}\, {\mathbf {G}})}$
, so we can take
${\mathbf {G}} \rightarrow \operatorname {\mathrm {Res}}_{F'/F}\operatorname {\mathrm {GL}}_{C^{linSpt}({\operatorname {dim}}\, {\mathbf {G}})}$
, so we can take
![]() $C^{lin}(n)=C^{linSpt}(n)C^{spt}(n)$
.
$C^{lin}(n)=C^{linSpt}(n)C^{spt}(n)$
.
B.2 Sketch of the proof of Lemma 3.2.1
We first show that there are finitely many root data of a given dimension (see Lemma B.3.1 below). Thus, we restrict our attention to a given root datum
![]() ${\mathfrak X}$
. We denote by
${\mathfrak X}$
. We denote by
![]() ${\mathcal G}$
the split reductive group scheme corresponding to
${\mathcal G}$
the split reductive group scheme corresponding to
![]() ${\mathfrak X}$
. By Lemma B.1.1, there is an integer k such that any reductive group of type
${\mathfrak X}$
. By Lemma B.1.1, there is an integer k such that any reductive group of type
![]() ${\mathfrak X}$
over a finite field splits after passing to a field extension of degree k.
${\mathfrak X}$
over a finite field splits after passing to a field extension of degree k.
We then construct a finite etale map of schemes
![]() ${\mathcal E}\to {\mathcal F}$
that forms a family containing all degree k extensions of finite fields. This means that, for any degree k extension of finite fields
${\mathcal E}\to {\mathcal F}$
that forms a family containing all degree k extensions of finite fields. This means that, for any degree k extension of finite fields
![]() $E/F$
, we can find an F-point y of
$E/F$
, we can find an F-point y of
![]() ${\mathcal F}$
whose fiber
${\mathcal F}$
whose fiber
![]() ${\mathcal E}_y$
is
${\mathcal E}_y$
is
![]() $\operatorname {\mathrm {Spec}} E$
. Moreover, we equip
$\operatorname {\mathrm {Spec}} E$
. Moreover, we equip
![]() $\mathcal {E}$
with an action of the cyclic group
$\mathcal {E}$
with an action of the cyclic group
![]() $C_k$
such that, if F is a finite field, we can find y as above such that the action of
$C_k$
such that, if F is a finite field, we can find y as above such that the action of
![]() $C_k$
on
$C_k$
on
![]() $\mathcal {E}_y$
is the Frobenius. See Lemma B.4.1 below.
$\mathcal {E}_y$
is the Frobenius. See Lemma B.4.1 below.
By Lang’s theorem, a reductive group of type
![]() ${\mathfrak X}$
over a finite field F that splits over a degree k extension
${\mathfrak X}$
over a finite field F that splits over a degree k extension
![]() $E/F$
is determined by an action of
$E/F$
is determined by an action of
![]() $C_k$
on
$C_k$
on
![]() ${\mathfrak X}$
. We show that there are finitely may such actions up to conjugation (see Lemma B.3.2 below). Thus, we can fix one such an action
${\mathfrak X}$
. We show that there are finitely may such actions up to conjugation (see Lemma B.3.2 below). Thus, we can fix one such an action
![]() $\xi $
. We can also consider
$\xi $
. We can also consider
![]() $\xi $
as an action on
$\xi $
as an action on
![]() ${\mathcal G}$
.
${\mathcal G}$
.
At this point, we can construct a group scheme
![]() ${\mathcal H} \to {\mathcal F}$
containing all groups of type
${\mathcal H} \to {\mathcal F}$
containing all groups of type
![]() $(\frak {X},\xi )$
over finite fields. Namely, we first construct a group scheme
$(\frak {X},\xi )$
over finite fields. Namely, we first construct a group scheme
![]() ${\mathcal H}'\to {\mathcal F}$
whose fiber over
${\mathcal H}'\to {\mathcal F}$
whose fiber over
![]() $y\in \mathcal {F}(F)$
is the restriction of scalars of
$y\in \mathcal {F}(F)$
is the restriction of scalars of
![]() ${\mathcal G}_{{\mathcal E}_y}$
to F. Using the two actions of
${\mathcal G}_{{\mathcal E}_y}$
to F. Using the two actions of
![]() $C_k$
on
$C_k$
on
![]() $\mathcal {E}$
and
$\mathcal {E}$
and
![]() $\mathcal {G}$
, we equip
$\mathcal {G}$
, we equip
![]() $\mathcal {H}'$
with an action of
$\mathcal {H}'$
with an action of
![]() $C_k$
. Finally, set
$C_k$
. Finally, set
![]() ${\mathcal H} := ({\mathcal H}' )^{C_k}$
.
${\mathcal H} := ({\mathcal H}' )^{C_k}$
.
Next, we incorporate all possible involutions. We first note that, up to inner automorphisms, there are only finitely many involutions of
![]() ${\mathfrak X}$
commuting with the action of
${\mathfrak X}$
commuting with the action of
![]() $C_k$
(see Lemma B.3.2 below). Thus, we can restrict our attention to a specific such involution
$C_k$
(see Lemma B.3.2 below). Thus, we can restrict our attention to a specific such involution
![]() $\eta $
. We then construct an
$\eta $
. We then construct an
![]() $\mathcal {F}$
-scheme
$\mathcal {F}$
-scheme
![]() ${\mathcal S}$
whose F-points are pairs
${\mathcal S}$
whose F-points are pairs
![]() $(y,t)$
consisting of a point
$(y,t)$
consisting of a point
![]() $y\in {\mathcal F}(F)$
and an involution t of
$y\in {\mathcal F}(F)$
and an involution t of
![]() ${\mathcal G}_{{\mathcal E}_y}$
which commutes with
${\mathcal G}_{{\mathcal E}_y}$
which commutes with
![]() $\xi $
and is of outer class
$\xi $
and is of outer class
![]() $\eta $
.
$\eta $
.
Finally, we pull back the group schemes
![]() ${\mathcal H}'$
and
${\mathcal H}'$
and
![]() ${\mathcal H}$
to
${\mathcal H}$
to
![]() ${\mathcal S}$
and denote the resulting groups schemes
${\mathcal S}$
and denote the resulting groups schemes
![]() ${\mathcal R}'$
and
${\mathcal R}'$
and
![]() ${\mathcal R}$
. Both
${\mathcal R}$
. Both
![]() $\mathcal {R}$
and
$\mathcal {R}$
and
![]() $\mathcal {R}'$
are equipped with a natural involution
$\mathcal {R}'$
are equipped with a natural involution
![]() $\tau $
. The group scheme
$\tau $
. The group scheme
![]() ${\mathcal R}\to {\mathcal S}$
with the involution
${\mathcal R}\to {\mathcal S}$
with the involution
![]() $\tau $
gives the required family.
$\tau $
gives the required family.
Remark B.2.1. In the proof, below we skip
![]() $\mathcal {H},\mathcal {H}'$
and construct
$\mathcal {H},\mathcal {H}'$
and construct
![]() $\mathcal {R},\mathcal {R}'$
directly.
$\mathcal {R},\mathcal {R}'$
directly.
B.3 Some preparations
Lemma B.3.1. For any integer
![]() $n>0$
, there is a finite number of isomorphism classes of complex connected reductive groups of dimension n.
$n>0$
, there is a finite number of isomorphism classes of complex connected reductive groups of dimension n.
Proof. Fix a complex connected reductive group
![]() ${\mathbf {G}}$
. Let
${\mathbf {G}}$
. Let
![]() $\tilde {\mathbf {G}}'$
be the universal cover of its derived group, let
$\tilde {\mathbf {G}}'$
be the universal cover of its derived group, let
![]() $Z^0({\mathbf {G}})$
be the connected component of the center of
$Z^0({\mathbf {G}})$
be the connected component of the center of
![]() ${\mathbf {G}}$
and let
${\mathbf {G}}$
and let
![]() $\Gamma $
be the kernel of the multiplication map
$\Gamma $
be the kernel of the multiplication map
![]() $\tilde {\mathbf {G}}' \times Z^0({\mathbf {G}}) \to {\mathbf {G}}$
.
$\tilde {\mathbf {G}}' \times Z^0({\mathbf {G}}) \to {\mathbf {G}}$
.
Let
![]() $Z(\tilde {\mathbf {G}}')$
be the center of
$Z(\tilde {\mathbf {G}}')$
be the center of
![]() $\tilde {\mathbf {G}}'$
. Note that
$\tilde {\mathbf {G}}'$
. Note that
![]() $Z(\tilde {{\mathbf {G}}}')$
is finite, that
$Z(\tilde {{\mathbf {G}}}')$
is finite, that
![]() $\Gamma \subset Z(\tilde {\mathbf {G}}') \times Z^0({\mathbf {G}})$
and that
$\Gamma \subset Z(\tilde {\mathbf {G}}') \times Z^0({\mathbf {G}})$
and that
![]() $\Gamma \cap Z^0({\mathbf {G}})$
is trivial. Thus,
$\Gamma \cap Z^0({\mathbf {G}})$
is trivial. Thus,
![]() $\Gamma $
is a graph of a morphism from subgroup of
$\Gamma $
is a graph of a morphism from subgroup of
![]() $Z(\tilde {\mathbf {G}}')$
to
$Z(\tilde {\mathbf {G}}')$
to
![]() $Z^0({\mathbf {G}})$
. This implies that
$Z^0({\mathbf {G}})$
. This implies that
![]() $\Gamma < Z(\tilde {\mathbf {G}}') \times Z^0({\mathbf {G}})[|Z(\tilde {\mathbf {G}}')|]$
, where for an integer k, the group
$\Gamma < Z(\tilde {\mathbf {G}}') \times Z^0({\mathbf {G}})[|Z(\tilde {\mathbf {G}}')|]$
, where for an integer k, the group
![]() $Z^0({\mathbf {G}})[k]$
is the subgroup of elements of order dividing k in
$Z^0({\mathbf {G}})[k]$
is the subgroup of elements of order dividing k in
![]() $Z^0({\mathbf {G}})$
.
$Z^0({\mathbf {G}})$
.
Any complex connected reductive group
![]() ${\mathbf {G}}$
is uniquely determined (up to isomorphism) by the following:
${\mathbf {G}}$
is uniquely determined (up to isomorphism) by the following:
-
• the simply conected semi-simple complex group
 $\tilde {\mathbf {G}}'$
.
$\tilde {\mathbf {G}}'$
. -
• the complex algebraic torus
 $Z^0({\mathbf {G}})$
.
$Z^0({\mathbf {G}})$
. -
• the finite subgroup
 $\Gamma < Z(\tilde {\mathbf {G}}') \times Z^0({\mathbf {G}})[|Z(\tilde {\mathbf {G}}')|]$
.
$\Gamma < Z(\tilde {\mathbf {G}}') \times Z^0({\mathbf {G}})[|Z(\tilde {\mathbf {G}}')|]$
.
Since each of those has only finitely many options given the dimension of
![]() ${\mathbf {G}}$
, the claim follows.
${\mathbf {G}}$
, the claim follows.
Lemma B.3.2. For any complex connected reductive group
![]() ${\mathbf {G}}$
and any finite abelian group A,
${\mathbf {G}}$
and any finite abelian group A,
Proof. Any automorphism of
![]() ${\mathbf {G}}$
is determined by its restrictions to the derived subgroup
${\mathbf {G}}$
is determined by its restrictions to the derived subgroup
![]() ${\mathbf {G}}'$
and to the connected component
${\mathbf {G}}'$
and to the connected component
![]() $Z^0({\mathbf {G}})$
of the center. We first claim that the map
$Z^0({\mathbf {G}})$
of the center. We first claim that the map
![]() $\operatorname {\mathrm {Aut}}({\mathbf {G}})\rightarrow \operatorname {\mathrm {Aut}}(Z^0({\mathbf {G}}))\times Aut({\mathbf {G}}')$
has finite cokernel. Indeed, let
$\operatorname {\mathrm {Aut}}({\mathbf {G}})\rightarrow \operatorname {\mathrm {Aut}}(Z^0({\mathbf {G}}))\times Aut({\mathbf {G}}')$
has finite cokernel. Indeed, let
![]() $\mathbf {K}$
be the kernel of the map
$\mathbf {K}$
be the kernel of the map
![]() ${\mathbf {G}}' \times Z^0({\mathbf {G}}) \rightarrow {\mathbf {G}}$
. The group
${\mathbf {G}}' \times Z^0({\mathbf {G}}) \rightarrow {\mathbf {G}}$
. The group
![]() $\mathbf {K}$
is finite. Let
$\mathbf {K}$
is finite. Let
![]() $\mathbf M \subset {\mathbf {G}}' \times Z^0({\mathbf {G}})$
be the product of the center
$\mathbf M \subset {\mathbf {G}}' \times Z^0({\mathbf {G}})$
be the product of the center
![]() $Z({\mathbf {G}}')$
and the finite group of elements of
$Z({\mathbf {G}}')$
and the finite group of elements of
![]() $Z^0({\mathbf {G}})$
of order dividing
$Z^0({\mathbf {G}})$
of order dividing
![]() $|\mathbf {K}|$
. The group
$|\mathbf {K}|$
. The group
![]() $\mathbf {M}$
is finite, contains
$\mathbf {M}$
is finite, contains
![]() $\mathbf {K}$
and is characteristic in
$\mathbf {K}$
and is characteristic in
![]() ${\mathbf {G}}' \times Z^0({\mathbf {G}})$
. It follows that the subgroup of
${\mathbf {G}}' \times Z^0({\mathbf {G}})$
. It follows that the subgroup of
![]() $\operatorname {\mathrm {Aut}}(Z^0({\mathbf {G}}))\times Aut({\mathbf {G}}')$
fixing
$\operatorname {\mathrm {Aut}}(Z^0({\mathbf {G}}))\times Aut({\mathbf {G}}')$
fixing
![]() $\mathbf {K}$
has finite index. Any element in this subgroup extends to an automorphism of
$\mathbf {K}$
has finite index. Any element in this subgroup extends to an automorphism of
![]() ${\mathbf {G}}$
.
${\mathbf {G}}$
.
Let
![]() $\phi $
be the composition
$\phi $
be the composition
![]() $Aut({\mathbf {G}})\rightarrow Aut(Z^0({\mathbf {G}}))\times Aut({\mathbf {G}}') \rightarrow Aut(Z^0({\mathbf {G}}))\times Out({\mathbf {G}}')$
. By the paragraph above, the cokernel of
$Aut({\mathbf {G}})\rightarrow Aut(Z^0({\mathbf {G}}))\times Aut({\mathbf {G}}') \rightarrow Aut(Z^0({\mathbf {G}}))\times Out({\mathbf {G}}')$
. By the paragraph above, the cokernel of
![]() $\phi $
is finite. Note also that the kernel of
$\phi $
is finite. Note also that the kernel of
![]() $\phi $
is the subgroup of inner automorphisms. In particular, we have an embedding
$\phi $
is the subgroup of inner automorphisms. In particular, we have an embedding
![]() $Out({\mathbf {G}}) \rightarrow Aut(Z^0({\mathbf {G}})) \times Out({\mathbf {G}}')$
with a finite cokernel.
$Out({\mathbf {G}}) \rightarrow Aut(Z^0({\mathbf {G}})) \times Out({\mathbf {G}}')$
with a finite cokernel.
The group
![]() $Out({\mathbf {G}}')$
is finite. Denote it by
$Out({\mathbf {G}}')$
is finite. Denote it by
![]() $\Gamma $
. The group
$\Gamma $
. The group
![]() $Aut(Z^0({\mathbf {G}}))$
is isomorphic to
$Aut(Z^0({\mathbf {G}}))$
is isomorphic to
![]() $GL_n(\mathbb {Z})$
for some integer n. We get
$GL_n(\mathbb {Z})$
for some integer n. We get
 $$ \begin{align*} |Mor(A,Out({\mathbf{G}}))/Ad(Out({\mathbf{G}}))|&\leq |Mor(A,GL_n(\mathbb{Z})\times \Gamma)/Ad(Out({\mathbf{G}}))| \\&\leq[GL_n(\mathbb{Z})\times \Gamma:Out({\mathbf{G}})] \cdot |Mor(A,GL_n(\mathbb{Z})\times \Gamma)/Ad(GL_n(\mathbb{Z})\times \Gamma)| \\&\leq [GL_n(\mathbb{Z})\times \Gamma:Out({\mathbf{G}})]\cdot |\Gamma| \cdot |Mor(A,GL_n(\mathbb{Z}))/Ad(GL_n(\mathbb{Z}))|. \end{align*} $$
$$ \begin{align*} |Mor(A,Out({\mathbf{G}}))/Ad(Out({\mathbf{G}}))|&\leq |Mor(A,GL_n(\mathbb{Z})\times \Gamma)/Ad(Out({\mathbf{G}}))| \\&\leq[GL_n(\mathbb{Z})\times \Gamma:Out({\mathbf{G}})] \cdot |Mor(A,GL_n(\mathbb{Z})\times \Gamma)/Ad(GL_n(\mathbb{Z})\times \Gamma)| \\&\leq [GL_n(\mathbb{Z})\times \Gamma:Out({\mathbf{G}})]\cdot |\Gamma| \cdot |Mor(A,GL_n(\mathbb{Z}))/Ad(GL_n(\mathbb{Z}))|. \end{align*} $$
By [Reference Platonov and RapinchukPR94, Theorem 4.3],
![]() $Mor(A,GL_n(\mathbb {Z}))/Ad(GL_n(\mathbb {Z}))$
is finite, proving the lemma.
$Mor(A,GL_n(\mathbb {Z}))/Ad(GL_n(\mathbb {Z}))$
is finite, proving the lemma.
B.4 Construction of the family
Lemma B.4.1. For any integer
![]() $n>0$
, there exists a finite etale morphism
$n>0$
, there exists a finite etale morphism
![]() $\Psi _n:{\mathcal E}_n\to {\mathcal F}_n$
of schemes of finite type over
$\Psi _n:{\mathcal E}_n\to {\mathcal F}_n$
of schemes of finite type over
![]() $\mathbb {Z}$
with an action of
$\mathbb {Z}$
with an action of
![]() $C_n$
on
$C_n$
on
![]() ${\mathcal E}_n$
over
${\mathcal E}_n$
over
![]() ${\mathcal F}_n$
such that, for any degree n extension
${\mathcal F}_n$
such that, for any degree n extension
![]() $E/F$
of finite fields, there exists
$E/F$
of finite fields, there exists
![]() $\nu :\operatorname {\mathrm {Spec}} F \to {\mathcal F}_n$
such that
$\nu :\operatorname {\mathrm {Spec}} F \to {\mathcal F}_n$
such that
as a
![]() $C_n$
-scheme. Here, the action of
$C_n$
-scheme. Here, the action of
![]() $C_n$
on E is the Galois action.
$C_n$
on E is the Galois action.
Proof. For a unital ring A and an integer k, let
![]() $A_k[t]$
be the set of polynomials of degree
$A_k[t]$
be the set of polynomials of degree
![]() $\leq k$
and let
$\leq k$
and let
![]() $A^{\prime }_k[t]$
be the set of monic polynomials of degree k. Denote the resultant of two polynomials
$A^{\prime }_k[t]$
be the set of monic polynomials of degree k. Denote the resultant of two polynomials
![]() $f(t),g(t)$
by
$f(t),g(t)$
by
![]() $res_t(f,g)$
. Let
$res_t(f,g)$
. Let
and let
Define an action of
![]() $C_n$
on
$C_n$
on
![]() ${\mathcal E}_n(A)$
by
${\mathcal E}_n(A)$
by
By construction, the assignments
![]() $A\mapsto {\mathcal F}_n(A)$
and
$A\mapsto {\mathcal F}_n(A)$
and
![]() $A\mapsto {\mathcal E}_n(A)$
give rise to representable functors. We denote the representing schemes by
$A\mapsto {\mathcal E}_n(A)$
give rise to representable functors. We denote the representing schemes by
![]() ${\mathcal F}_n$
and
${\mathcal F}_n$
and
![]() ${\mathcal E}_n$
. Similarly, the action of
${\mathcal E}_n$
. Similarly, the action of
![]() $C_n$
on
$C_n$
on
![]() ${\mathcal E}_n(A)$
gives rise to an action of
${\mathcal E}_n(A)$
gives rise to an action of
![]() $C_n$
on
$C_n$
on
![]() ${\mathcal E}_n$
over
${\mathcal E}_n$
over
![]() ${\mathcal F}_n$
. Denote by
${\mathcal F}_n$
. Denote by
![]() $\Psi _n:{\mathcal E}_n \to {\mathcal F}_n$
the projection. The map
$\Psi _n:{\mathcal E}_n \to {\mathcal F}_n$
the projection. The map
![]() $\Psi _n$
is an etale map.
$\Psi _n$
is an etale map.
Suppose that
![]() $E/F$
is a degree n extension of finite fields. Let
$E/F$
is a degree n extension of finite fields. Let
![]() $\alpha \in E$
be a generator and let
$\alpha \in E$
be a generator and let
![]() $f\in F_n[t]$
be its (monic) minimal polynomial. Let
$f\in F_n[t]$
be its (monic) minimal polynomial. Let
![]() $g\in F_{n-1}[t]$
be the polynomial of degree
$g\in F_{n-1}[t]$
be the polynomial of degree
![]() $<n$
such that
$<n$
such that
![]() $Fr_F(\alpha )=g(\alpha )$
. The tuple
$Fr_F(\alpha )=g(\alpha )$
. The tuple
![]() $(f,g)$
is a point in
$(f,g)$
is a point in
![]() ${\mathcal F}_n(F)$
(i.e., it defines a morphism
${\mathcal F}_n(F)$
(i.e., it defines a morphism
![]() $\operatorname {\mathrm {Spec}} F\to {\mathcal F}_n$
). It is easy to see that
$\operatorname {\mathrm {Spec}} F\to {\mathcal F}_n$
). It is easy to see that
as required.
We now prove the main result of this appendix.
Proof of Lemma 3.2.1.
Let
![]() ${\mathfrak X}$
be a pair consisting of a root datum and a choice of positive roots, and let k be an integer. Let
${\mathfrak X}$
be a pair consisting of a root datum and a choice of positive roots, and let k be an integer. Let
![]() $\alpha :S_2\times C_k\to Aut({\mathfrak X})$
be a morphism.
$\alpha :S_2\times C_k\to Aut({\mathfrak X})$
be a morphism.
Let
![]() ${\mathcal G}_{\mathfrak X}\to \operatorname {\mathrm {Spec}} \mathbb {Z}$
be the split reductive group scheme corresponding to
${\mathcal G}_{\mathfrak X}\to \operatorname {\mathrm {Spec}} \mathbb {Z}$
be the split reductive group scheme corresponding to
![]() ${\mathfrak X}$
. Let
${\mathfrak X}$
. Let
![]() ${\alpha }_2:S_2\times C_k\to Aut({\mathcal G}_{\mathfrak X})$
be the corresponding action.
${\alpha }_2:S_2\times C_k\to Aut({\mathcal G}_{\mathfrak X})$
be the corresponding action.
Let
![]() $Aut_{{\mathcal G}_{{\mathfrak X}}/\mathbb {Z}}:Schemes^{op} \to Groups$
be the functor defined by
$Aut_{{\mathcal G}_{{\mathfrak X}}/\mathbb {Z}}:Schemes^{op} \to Groups$
be the functor defined by
![]() $Aut_{{\mathcal G}_{{\mathfrak X}}/\mathbb {Z}}(S)=Aut_{S}({\mathcal G}_{{\mathfrak X}}\times _{\operatorname {\mathrm {Spec}}\mathbb {Z}}S)$
; cf. [Reference ConradCon, Definition 7.1.3]. By [Reference ConradCon, Theorem 7.1.9], this functor is representable by a (not necessarily finite type)
$Aut_{{\mathcal G}_{{\mathfrak X}}/\mathbb {Z}}(S)=Aut_{S}({\mathcal G}_{{\mathfrak X}}\times _{\operatorname {\mathrm {Spec}}\mathbb {Z}}S)$
; cf. [Reference ConradCon, Definition 7.1.3]. By [Reference ConradCon, Theorem 7.1.9], this functor is representable by a (not necessarily finite type)
![]() $\mathbb {Z}$
-group scheme that we also denote
$\mathbb {Z}$
-group scheme that we also denote
![]() $Aut_{{\mathcal G}_{{\mathfrak X}}/\mathbb {Z}}$
.
$Aut_{{\mathcal G}_{{\mathfrak X}}/\mathbb {Z}}$
.
Denoting
![]() $S_2=\left\{ 1,{\varepsilon } \right\}$
, let
$S_2=\left\{ 1,{\varepsilon } \right\}$
, let
![]() ${\mathcal I}_{{\mathfrak X},\alpha }\subset Aut_{{\mathcal G}_{{\mathfrak X}}/\mathbb {Z}}$
be defined by
${\mathcal I}_{{\mathfrak X},\alpha }\subset Aut_{{\mathcal G}_{{\mathfrak X}}/\mathbb {Z}}$
be defined by
 $$\begin{align*}{\mathcal I}_{{\mathfrak X},\alpha}(S):=\left\{ a \in Aut_{{\mathcal G}_{{\mathfrak X}}/\mathbb{Z}}(S) \left\vert \begin{array}{l} a\ \text{commutes with}\ {\alpha}_2(C_k)_S\ \text{and, for every geometric point}\ s\ \text{of}\ S,\\ \text{the automorphism}\ a_s\ \text{is in the class}\ \alpha({\varepsilon},0) \end{array} \!\!\right. \right\}, \end{align*}$$
$$\begin{align*}{\mathcal I}_{{\mathfrak X},\alpha}(S):=\left\{ a \in Aut_{{\mathcal G}_{{\mathfrak X}}/\mathbb{Z}}(S) \left\vert \begin{array}{l} a\ \text{commutes with}\ {\alpha}_2(C_k)_S\ \text{and, for every geometric point}\ s\ \text{of}\ S,\\ \text{the automorphism}\ a_s\ \text{is in the class}\ \alpha({\varepsilon},0) \end{array} \!\!\right. \right\}, \end{align*}$$
where S is an affine scheme. For an automorphism
![]() $\beta $
of
$\beta $
of
![]() ${\mathcal G}_{{\mathfrak X}}$
, we denote by
${\mathcal G}_{{\mathfrak X}}$
, we denote by
![]() $\beta _S$
its restriction to
$\beta _S$
its restriction to
![]() ${\mathcal G}_{{\mathfrak X}} \times S$
. By [Reference ConradCon, Theorem 7.1.9],
${\mathcal G}_{{\mathfrak X}} \times S$
. By [Reference ConradCon, Theorem 7.1.9],
![]() ${\mathcal I}_{{\mathfrak X},\alpha }$
is of finite type.
${\mathcal I}_{{\mathfrak X},\alpha }$
is of finite type.
Define an action
![]() ${\alpha }_3:S_2\times C_k\to Aut_{{\mathcal I}_{{\mathfrak X},\alpha }}( {\mathcal G}_{{\mathfrak X}} \times _{} {\mathcal I}_{{\mathfrak X},\alpha })$
by
${\alpha }_3:S_2\times C_k\to Aut_{{\mathcal I}_{{\mathfrak X},\alpha }}( {\mathcal G}_{{\mathfrak X}} \times _{} {\mathcal I}_{{\mathfrak X},\alpha })$
by
where
![]() $i\in \mathbb {Z}, j\in C_k$
and
$i\in \mathbb {Z}, j\in C_k$
and
![]() $(x,\eta )\in {\mathcal G}_{{\mathfrak X}} \times _{} {\mathcal I}_{{\mathfrak X},\alpha }(S)$
.
$(x,\eta )\in {\mathcal G}_{{\mathfrak X}} \times _{} {\mathcal I}_{{\mathfrak X},\alpha }(S)$
.
Let
![]() $\mathcal {F}_k,\mathcal {E}_k$
be as in Lemma B.4.1 and define
$\mathcal {F}_k,\mathcal {E}_k$
be as in Lemma B.4.1 and define
![]() ${\mathcal S}_{{\mathfrak X},\alpha }:=(\mathcal {I}_{\frak {X},\alpha } \times {\mathcal {F}}_k)\,^{\wedge }_{\mathcal {F}_k} {\mathcal {E}}_k$
, where
${\mathcal S}_{{\mathfrak X},\alpha }:=(\mathcal {I}_{\frak {X},\alpha } \times {\mathcal {F}}_k)\,^{\wedge }_{\mathcal {F}_k} {\mathcal {E}}_k$
, where
![]() $^{\wedge }$
denotes the internal morphism space; see, for example, [Reference Aizenbud and AvniAA, §§3.1]. An F-point of
$^{\wedge }$
denotes the internal morphism space; see, for example, [Reference Aizenbud and AvniAA, §§3.1]. An F-point of
![]() $\mathcal {S}_{\frak {X},\alpha }$
is a pair
$\mathcal {S}_{\frak {X},\alpha }$
is a pair
![]() $(z,y)$
, where
$(z,y)$
, where
![]() $y\in \mathcal {F}_k(F)$
and
$y\in \mathcal {F}_k(F)$
and
![]() $z\in \mathcal {I}_{\frak {X},\alpha }((\mathcal {E}_k)_y)$
. Let
$z\in \mathcal {I}_{\frak {X},\alpha }((\mathcal {E}_k)_y)$
. Let
Note that
![]() ${\mathcal R}^{\prime }_{{\mathfrak X},\alpha }$
has a natural structure of a group scheme over
${\mathcal R}^{\prime }_{{\mathfrak X},\alpha }$
has a natural structure of a group scheme over
![]() ${\mathcal S}_{{\mathfrak X},\alpha }$
. By their constructions,
${\mathcal S}_{{\mathfrak X},\alpha }$
. By their constructions,
![]() $\mathcal {E}_k,\mathcal {S}_{\frak {X},\alpha },\mathcal {R}^{\prime }_{\frak {X},\alpha }$
all have an action of
$\mathcal {E}_k,\mathcal {S}_{\frak {X},\alpha },\mathcal {R}^{\prime }_{\frak {X},\alpha }$
all have an action of
![]() $S_2 \times C_k$
(
$S_2 \times C_k$
(
![]() $S_2$
acts trivially on
$S_2$
acts trivially on
![]() $\mathcal {E}_k$
). Denoting the
$\mathcal {E}_k$
). Denoting the
![]() $S_2 \times C_k$
-action on
$S_2 \times C_k$
-action on
![]() $\mathcal {R}^{\prime }_{\mathfrak {X},\alpha }$
by
$\mathcal {R}^{\prime }_{\mathfrak {X},\alpha }$
by
let
and
Denote
![]() $n_{\mathfrak X}:=C^{spt}({\operatorname {dim}}_{\operatorname {\mathrm {Spec}} \mathbb {Z}}({\mathcal G}_{\mathfrak X})),$
where
$n_{\mathfrak X}:=C^{spt}({\operatorname {dim}}_{\operatorname {\mathrm {Spec}} \mathbb {Z}}({\mathcal G}_{\mathfrak X})),$
where
![]() $C^{spt}$
is the function given by Lemma B.1.1.
$C^{spt}$
is the function given by Lemma B.1.1.
Let
Since there are finitely many root data of a given dimension (Lemma B.3.1) and finitely many actions of
![]() $S_2\times C_d$
(
$S_2\times C_d$
(
![]() $d \leq n_{{\mathfrak X}}$
) on a given root datum (Lemma B.3.2), the set
$d \leq n_{{\mathfrak X}}$
) on a given root datum (Lemma B.3.2), the set
![]() $\Delta _n$
is finite. Finally, set
$\Delta _n$
is finite. Finally, set
 $$ \begin{align*}{\mathcal S}_{n}:=\bigsqcup_{({\mathfrak X},d,[\alpha]) \in \Delta_n} {\mathcal S}_{{\mathfrak X},\alpha},\end{align*} $$
$$ \begin{align*}{\mathcal S}_{n}:=\bigsqcup_{({\mathfrak X},d,[\alpha]) \in \Delta_n} {\mathcal S}_{{\mathfrak X},\alpha},\end{align*} $$
 $$ \begin{align*}{\mathcal R}_{n}:=\bigsqcup_{({\mathfrak X},d,[\alpha]) \in \Delta_n} {\mathcal R}_{{\mathfrak X},\alpha},\end{align*} $$
$$ \begin{align*}{\mathcal R}_{n}:=\bigsqcup_{({\mathfrak X},d,[\alpha]) \in \Delta_n} {\mathcal R}_{{\mathfrak X},\alpha},\end{align*} $$
and
 $$ \begin{align*}t_{n}:=\bigsqcup_{({\mathfrak X},d,[\alpha]) \in \Delta_n} t_{{\mathfrak X},\alpha}.\end{align*} $$
$$ \begin{align*}t_{n}:=\bigsqcup_{({\mathfrak X},d,[\alpha]) \in \Delta_n} t_{{\mathfrak X},\alpha}.\end{align*} $$
We claim that
![]() $({\mathcal R}_{n},{\mathcal S}_{n},t_n)$
satisfies the requirements of the lemma.
$({\mathcal R}_{n},{\mathcal S}_{n},t_n)$
satisfies the requirements of the lemma.
Parts (1,3) follow from the fact that, for any geometric point x of
![]() ${\mathcal S}_{{\mathfrak X},\alpha }$
, the group scheme
${\mathcal S}_{{\mathfrak X},\alpha }$
, the group scheme
![]() $({\mathcal R}_{{\mathfrak X},\alpha })_x$
is reductive and its absolute root system is
$({\mathcal R}_{{\mathfrak X},\alpha })_x$
is reductive and its absolute root system is
![]() ${\mathfrak X}$
. It remains to show Part (2).
${\mathfrak X}$
. It remains to show Part (2).
Let n be an integer, let F be a finite field, let
![]() ${\mathbf {G}}$
be a reductive group of dimension
${\mathbf {G}}$
be a reductive group of dimension
![]() $\leq n$
defined over F and let t be an involution of
$\leq n$
defined over F and let t be an involution of
![]() ${\mathbf {G}}$
. We need to find an element
${\mathbf {G}}$
. We need to find an element
![]() $w\in {\mathcal S}_n(F)$
such that
$w\in {\mathcal S}_n(F)$
such that
Let
![]() ${\mathfrak X}$
be the absolute root datum of
${\mathfrak X}$
be the absolute root datum of
![]() ${\mathbf {G}}$
. By Lemma B.1.1, there is a field extension
${\mathbf {G}}$
. By Lemma B.1.1, there is a field extension
![]() $E/F$
of degree
$E/F$
of degree
![]() $d \leq n_{\frak {X}}$
and an isomorphism
$d \leq n_{\frak {X}}$
and an isomorphism
![]() ${\mathbf {G}}_E \simeq (\mathcal {G}_{\frak {X}})_E$
.
${\mathbf {G}}_E \simeq (\mathcal {G}_{\frak {X}})_E$
.
Denoting the group of E-automorphisms of the algebraic group
![]() $(\mathcal {G}_{\frak {X}})_{E}$
by
$(\mathcal {G}_{\frak {X}})_{E}$
by
![]() $Aut_{E} \left( (\mathcal {G}_{\frak {X}})_{E} \right)$
, we get an element in
$Aut_{E} \left( (\mathcal {G}_{\frak {X}})_{E} \right)$
, we get an element in
![]() $H^1(Gal(E/F),Aut_{E}(({\mathcal G}_{\mathfrak X})_{E}))$
. By Lang’s theorem, this element comes from an element
$H^1(Gal(E/F),Aut_{E}(({\mathcal G}_{\mathfrak X})_{E}))$
. By Lang’s theorem, this element comes from an element
![]() $H^1(Gal(E/F),Out_{E} (({\mathcal G}_{\mathfrak X})_{E}))$
via the embedding
$H^1(Gal(E/F),Out_{E} (({\mathcal G}_{\mathfrak X})_{E}))$
via the embedding
![]() $Out_{E}( ({\mathcal G}_{\mathfrak X})_{E})\cong Out({\mathfrak X})\subset Aut_{E} ({\mathcal G}_{\mathfrak X})_{E}$
. Since the action of
$Out_{E}( ({\mathcal G}_{\mathfrak X})_{E})\cong Out({\mathfrak X})\subset Aut_{E} ({\mathcal G}_{\mathfrak X})_{E}$
. Since the action of
![]() $\operatorname {\mathrm {Gal}}(E/F)$
on
$\operatorname {\mathrm {Gal}}(E/F)$
on
![]() $Out_{E}\left( ({\mathcal G}_{\mathfrak X})_{E} \right)$
is trivial, this element is a homomorphism
$Out_{E}\left( ({\mathcal G}_{\mathfrak X})_{E} \right)$
is trivial, this element is a homomorphism
![]() $\xi : Gal(E/F)\to Out_{E} \left( ({\mathcal G}_{{\mathfrak X}})_{E} \right)=Aut({\mathfrak X})$
.
$\xi : Gal(E/F)\to Out_{E} \left( ({\mathcal G}_{{\mathfrak X}})_{E} \right)=Aut({\mathfrak X})$
.
Let
![]() $[t]\in Aut({\mathfrak X})$
be the involution corresponding to
$[t]\in Aut({\mathfrak X})$
be the involution corresponding to
![]() $t\in \operatorname {\mathrm {Aut}}({\mathbf {G}})$
. We get an action
$t\in \operatorname {\mathrm {Aut}}({\mathbf {G}})$
. We get an action
![]() $\alpha :S_2\times C_d\to Aut({\mathfrak X})$
. By Lemma B.4.1, there is an element
$\alpha :S_2\times C_d\to Aut({\mathfrak X})$
. By Lemma B.4.1, there is an element
![]() $y\in {\mathcal F}_d(F)$
such that
$y\in {\mathcal F}_d(F)$
such that
![]() $({\mathcal E}_d)|_y=\operatorname {\mathrm {Spec}} E$
and the action
$({\mathcal E}_d)|_y=\operatorname {\mathrm {Spec}} E$
and the action
![]() $C_d$
on this fiber is the Frobenius action.
$C_d$
on this fiber is the Frobenius action.
Let
![]() $t_{E}$
be the automorphism of
$t_{E}$
be the automorphism of
![]() ${\mathbf {G}}_{E}$
corresponding to t. We will consider it as an element in
${\mathbf {G}}_{E}$
corresponding to t. We will consider it as an element in
![]() $Aut_{{\mathcal G}_X/\mathbb {Z}}(E)=Aut_E\left( (\mathcal {G}_{\frak {X}})_E \right)$
. By construction,
$Aut_{{\mathcal G}_X/\mathbb {Z}}(E)=Aut_E\left( (\mathcal {G}_{\frak {X}})_E \right)$
. By construction,
![]() $t\in {\mathcal I}_{{\mathfrak X},\alpha }(F)$
. The tuple
$t\in {\mathcal I}_{{\mathfrak X},\alpha }(F)$
. The tuple
![]() $(y,t)$
gives a point
$(y,t)$
gives a point
![]() $w\in {\mathcal S}_{{\mathfrak X},\alpha }(F) \subset {\mathcal S}_n(F)$
. Finally,
$w\in {\mathcal S}_{{\mathfrak X},\alpha }(F) \subset {\mathcal S}_n(F)$
. Finally,
Acknowledgements
We thank Uri Bader, Shachar Carmeli, Yoav Segev and Shai Shechter for helpful discussions.
Competing interest
The authors have no competing interest to declare.
Financial support
A.A. was partially supported by ISF grant 249/17 and a Minerva foundation grant. N.A. was partially supported by NSF grant DMS-1902041. We were both partially supported by BSF grant 2018201.