Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-23T05:36:06.576Z Has data issue: false hasContentIssue false
  • English
  • Français

GEOMETRIC BIJECTIONS FOR REGULAR MATROIDS, ZONOTOPES, AND EHRHART THEORY

Part of: Polytopes and polyhedra Algebraic combinatorics Graph theory Discrete geometry

Published online by Cambridge University Press:  04 December 2019

SPENCER BACKMAN ,
MATTHEW BAKER  and
CHI HO YUEN
SPENCER BACKMAN
Affiliation:
Department of Mathematics and Statistics, University of Vermont, Innovation Hall 82 University Place, Burlington, VT05405, USA; spencer.backman@uvm.edu
MATTHEW BAKER
Affiliation:
School of Mathematics, Georgia Institute of Technology Atlanta, GA 30332-0160, USA; mbaker@math.gatech.edu
CHI HO YUEN
Affiliation:
Division of Applied Mathematics, Brown University, Providence, RI02912, USA; Chi_Ho_Yuen@Brown.edu

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 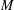$M$ be a regular matroid. The Jacobian group 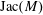$\text{Jac}(M)$ of 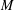$M$ is a finite abelian group whose cardinality is equal to the number of bases of 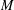$M$. This group generalizes the definition of the Jacobian group (also known as the critical group or sandpile group) 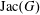$\operatorname{Jac}(G)$ of a graph 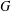$G$ (in which case bases of the corresponding regular matroid are spanning trees of 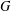$G$). There are many explicit combinatorial bijections in the literature between the Jacobian group of a graph 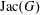$\text{Jac}(G)$ and spanning trees. However, most of the known bijections use vertices of 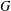$G$ in some essential way and are inherently ‘nonmatroidal’. In this paper, we construct a family of explicit and easy-to-describe bijections between the Jacobian group of a regular matroid 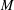$M$ and bases of 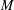$M$, many instances of which are new even in the case of graphs. We first describe our family of bijections in a purely combinatorial way in terms of orientations; more specifically, we prove that the Jacobian group of 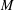$M$ admits a canonical simply transitive action on the set 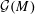${\mathcal{G}}(M)$ of circuit–cocircuit reversal classes of 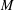$M$, and then define a family of combinatorial bijections 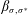$\unicode[STIX]{x1D6FD}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}^{\ast }}$ between 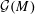${\mathcal{G}}(M)$ and bases of 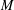$M$. (Here $\unicode[STIX]{x1D70E}$ (respectively 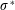$\unicode[STIX]{x1D70E}^{\ast }$) is an acyclic signature of the set of circuits (respectively cocircuits) of 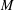$M$.) We then give a geometric interpretation of each such map 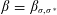$\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D6FD}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}^{\ast }}$ in terms of zonotopal subdivisions which is used to verify that 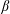$\unicode[STIX]{x1D6FD}$ is indeed a bijection. Finally, we give a combinatorial interpretation of lattice points in the zonotope 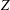$Z$; by passing to dilations we obtain a new derivation of Stanley’s formula linking the Ehrhart polynomial of 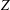$Z$ to the Tutte polynomial of 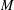$M$.

MSC classification

Primary: 52C40: Oriented matroids
Secondary: 05C31: Graph polynomials 05E18: Group actions on combinatorial structures 52B20: Lattice polytopes (including relations with commutative algebra and algebraic geometry) 52B40: Matroids (realizations in the context of convex polytopes, convexity in combinatorial structures, etc.)
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 7 , 2019 , e45
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2019

References

An, Y., Baker, M., Kuperberg, G. and Shokrieh, F., ‘Canonical representatives for divisor classes on tropical curves and the Matrix–Tree Theorem’, inForum of Mathematics, Sigma Vol. 2 (Cambridge University Press, Cambridge, United Kingdom, 2014), e24.Google Scholar
Bacher, R., La Harpe, P. de and Nagnibeda, T., ‘The lattice of integral flows and the lattice of integral cuts on a finite graph’, Bull. Soc. Math. France 125(2) (1997), 167–198.Google Scholar
Backman, S., ‘Riemann-Roch theory for graph orientations’, Adv. Math. 309 (2017), 655–691.Google Scholar
Backman, S., ‘Partial graph orientations and the Tutte polynomial’, Adv. Appl. Math. 94 (2018), 103–119.Google Scholar
Backman, S., Hopkins, S. and Traldi, L., ‘Fourientation activities and the Tutte polynomial’, European J. Combin. 67 (2018), 40–60.Google Scholar
Baker, M. and Faber, X., ‘Metrized graphs, Laplacian operators, and electrical networks’, inQuantum Graphs and their Applications, Contemporary Mathematics, 415 (American Mathematical Society, Providence, RI, 2006), 15–33.Google Scholar
Baker, M. and Shokrieh, F., ‘Chip-firing games, potential theory on graphs, and spanning trees’, J. Combin. Theory Ser. A 120(1) (2013), 164–182.Google Scholar
Baker, M. and Wang, Y., ‘The Bernardi process and torsor structures on spanning trees’, Int. Math. Res. Not. IMRN 16 (2018), 5120–5147.Google Scholar
Bernardi, O., ‘Tutte polynomial, subgraphs, orientations and sandpile model: new connections via embeddings’, Electron. J. Combin. 15(1) (2008).Google Scholar
Björner, A., Las Vergnas, M., Sturmfels, B., White, N. and Ziegler, G. M., Oriented Matroids, Encyclopedia of Mathematics and its Applications, 46 (Cambridge University Press, Cambridge, 1999).Google Scholar
Bohne, J., ‘Eine kombinatorische Analyse zonotopaler Raumaufteilungen’, PhD Thesis, Universität Bielefeld, 1992.Google Scholar
Chan, M., Church, T. and Grochow, J. A., ‘Rotor-routing and spanning trees on planar graphs’, Int. Math. Res. Not. IMRN 11 (2015), 3225–3244.Google Scholar
Chan, M., Glass, D., Macauley, M., Perkinson, D., Werner, C. and Yang, Q., ‘Sandpiles, spanning trees, and plane duality’, SIAM J. Discrete Math. 29(1) (2015), 461–471.Google Scholar
Cori, R. and Le Borgne, Y., ‘The sand-pile model and Tutte polynomials’, Adv. Appl. Math. 30(1–2) (2003), 44–52. Formal Power Series and Algebraic Combinatorics (Scottsdale, AZ, 2001).Google Scholar
D’Adderio, M. and Moci, L., ‘Ehrhart polynomial and arithmetic Tutte polynomial’, European J. Combin. 33(7) (2012), 1479–1483.Google Scholar
Dall, A. and Pfeifle, J., ‘A polyhedral proof of the Matrix Tree Theorem’, Preprint, 2014,arXiv:1404.3876.Google Scholar
Dress, A., Oriented matroids and Penrose-type tilings, August 1989. Lecture at the ‘Symposium on Combinatorics and Geometry’, organized by A. Björner, KTH Stockholm.Google Scholar
Dyer, M. and Frieze, A., ‘Random walks, totally unimodular matrices, and a randomised dual simplex algorithm’, Math. Program. 64(1, Ser. A) (1994), 1–16.Google Scholar
Ehrhart, E., ‘Sur les polyèdres homothétiques bordés à n dimensions’, C. R. Acad. Sci. 254 (1962).Google Scholar
Gioan, E., ‘Correspondance naturelle entre bases et réorientations des matroïes orientés, PhD Thesis, University of Bordeaux 1, 2002.Google Scholar
Gioan, E., ‘Enumerating degree sequences in digraphs and a cycle–cocycle reversing system’, European J. Combin. 28(4) (2007), 1351–1366.Google Scholar
Gioan, E., ‘Circuit–cocircuit reversing systems in regular matroids’, Ann. Combin. 12(2) (2008), 171–182.Google Scholar
Gioan, E. and Las Vergnas, M., ‘Activity preserving bijections between spanning trees and orientations in graphs’, Discrete Math. 298(1) (2005), 169–188.Google Scholar
Godsil, C. and Royle, G. F., Algebraic Graph Theory, Vol. 207, (Springer, New York, 2013).Google Scholar
Hopkins, S. and Perkinson, D., ‘Bigraphical arrangements’, Trans. Amer. Math. Soc. 368(1) (2016), 709–725.Google Scholar
Lipton, R., ‘A new approach to random spanning trees’, 2009. Available at https://rjlipton.wordpress.com/2009/07/15/a-new-approach-to-random-spanning-trees/.Google Scholar
Maurer, S., ‘Matrix generalizations of some theorems on trees, cycles and cocycles in graphs’, SIAM J. Appl. Math. 30(1) (1976), 143–148.Google Scholar
Merino, C., ‘Matroids, the Tutte polynomial and the chip firing game’, PhD Thesis, University of Oxford, 1999.Google Scholar
Oxley, J., Matroid Theory, 2nd edn, Oxford Graduate Texts in Mathematics, 21 (Oxford University Press, Oxford, 2011).Google Scholar
Perkinson, D., Yang, Q. and Yu, K., ‘ G-parking functions and tree inversions’, Combinatorica 37(2) (2017), 269–282.Google Scholar
Schrijver, A., Theory of Linear and Integer Programming, (Wiley, New York, 1998).Google Scholar
Shephard, G. C., ‘Combinatorial properties of associated zonotopes’, Canad. J. Math. 26 (1974), 302–321.Google Scholar
Shokrieh, F., ‘Matroids and their Jacobians’, in preparation.Google Scholar
Stanley, R. P., ‘A zonotope associated with graphical degree sequences’, inApplied Geometry and Discrete Mathematics, Series in Discrete Mathematics and Theoretical Computer Science, 4 (American Mathematical Society, Providence, RI, 1991), 555–570.Google Scholar
Su, Y. and Wagner, D. G., ‘The lattice of integer flows of a regular matroid’, J. Combin. Theory Ser. B 100(6) (2010), 691–703.Google Scholar
Welsh, D., ‘The Tutte polynomial’, Random Structures Algorithms 15(3–4) (1999), 210–228. Statistical Physics Methods in Discrete Probability, Combinatorics, and Theoretical Computer Science (Princeton, NJ, 1997).Google Scholar
Welsh, D. and Gale, A., ‘The complexity of counting problems’, inAspects of Complexity (Kaikoura, 2000), de Gruyter Series in Logic and its Applications, 4 (de Gruyter, Berlin, 2001), 115–153.Google Scholar
Yuen, C. H., ‘Geometric bijections between spanning trees and break divisors’, J. Combin. Theory Ser. A 152 (2017), 159–189.Google Scholar
Ziegler, G. M., Lectures on Polytopes, Graduate Texts in Mathematics, 152 (Springer, New York, 1995).Google Scholar