Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-18T08:57:47.157Z Has data issue: false hasContentIssue false
  • English
  • Français

GLOBAL WELL-POSEDNESS OF THE PERIODIC CUBIC FOURTH ORDER NLS IN NEGATIVE SOBOLEV SPACES

Part of: Equations of mathematical physics and other areas of application

Published online by Cambridge University Press:  11 May 2018

TADAHIRO OH  and
YUZHAO WANG
TADAHIRO OH
Affiliation:
School of Mathematics, The University of Edinburgh, and The Maxwell Institute for the Mathematical Sciences, James Clerk Maxwell Building, The King’s Buildings, Peter Guthrie Tait Road, Edinburgh EH9 3FD, UK; hiro.oh@ed.ac.uk
YUZHAO WANG
Affiliation:
School of Mathematics, The University of Edinburgh, and The Maxwell Institute for the Mathematical Sciences, James Clerk Maxwell Building, The King’s Buildings, Peter Guthrie Tait Road, Edinburgh EH9 3FD, UK; hiro.oh@ed.ac.uk School of Mathematics, Watson BuildingUniversity of Birmingham, Edgbaston, Birmingham B15 2TT, UK; y.wang.14@bham.ac.uk

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

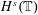We consider the Cauchy problem for the cubic fourth order nonlinear Schrödinger equation (4NLS) on the circle. In particular, we prove global well-posedness of the renormalized 4NLS in negative Sobolev spaces $H^{s}(\mathbb{T})$, 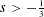$s>-\frac{1}{3}$, with enhanced uniqueness. The proof consists of two separate arguments. (i) We first prove global existence in 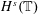$H^{s}(\mathbb{T})$, 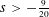$s>-\frac{9}{20}$, via the short-time Fourier restriction norm method. By following the argument in Guo–Oh for the cubic NLS, this also leads to nonexistence of solutions for the (nonrenormalized) 4NLS in negative Sobolev spaces. (ii) We then prove enhanced uniqueness in 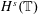$H^{s}(\mathbb{T})$, 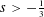$s>-\frac{1}{3}$, by establishing an energy estimate for the difference of two solutions with the same initial condition. For this purpose, we perform an infinite iteration of normal form reductions on the 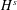$H^{s}$-energy functional, allowing us to introduce an infinite sequence of correction terms to the 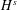$H^{s}$-energy functional in the spirit of the 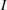$I$-method. In fact, the main novelty of this paper is this reduction of the 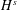$H^{s}$-energy functionals (for a single solution and for the difference of two solutions with the same initial condition) to sums of infinite series of multilinear terms of increasing degrees.

MSC classification

Primary: 35Q55: NLS-like equations (nonlinear Schrödinger)
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 6 , 2018 , e5
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2018

References

Babin, A., Ilyin, A. and Titi, E., ‘On the regularization mechanism for the periodic Korteweg–de Vries equation’, Comm. Pure Appl. Math. 64(5) (2011), 591–648.CrossRefGoogle Scholar
Ben-Artzi, M., Koch, H. and Saut, J. C., ‘Dispersion estimates for fourth order Schrödinger equations’, C. R. Acad. Sci. Paris Sér. I Math. 330(2) (2000), 87–92.Google Scholar
Bourgain, J., ‘Fourier transform restriction phenomena for certain lattice subsets and applications to nonlinear evolution equations I. Schrödinger equations’, Geom. Funct. Anal. 3(2) (1993), 107–156.Google Scholar
Bourgain, J., ‘Invariant measures for the 2D-defocusing nonlinear Schrödinger equation’, Comm. Math. Phys. 176(2) (1996), 421–445.Google Scholar
Burq, N., Gérard, P. and Tzvetkov, N., ‘An instability property of the nonlinear Schrödinger equation on S d ’, Math. Res. Lett. 9(2–3) (2002), 323–335.CrossRefGoogle Scholar
Choffrut, A. and Pocovnicu, O., ‘Ill-posedness for the cubic nonlinear half-wave equation and other fractional NLS on the real line’, Int. Math. Res. Not. IMRN 2018(3) 699–738.Google Scholar
Christ, M., ‘Nonuniqueness of weak solutions of the nonlinear Schrödinger equation’, Preprint, 2005, arXiv:math/0503366v1 [math.AP].Google Scholar
Christ, M., Colliander, J. and Tao, T., ‘Asymptotics, frequency modulation, and low regularity ill-posedness for canonical defocusing equations’, Amer. J. Math. 125(6) (2003), 1235–1293.Google Scholar
Christ, M., Colliander, J. and Tao, T., ‘Ill-posedness for nonlinear Schrödinger and wave equations’, Preprint, 2003, arXiv:math/0311048 [math.AP].Google Scholar
Christ, M., Colliander, J. and Tao, T., ‘ A priori bounds and weak solutions for the nonlinear Schrödinger equation in Sobolev spaces of negative order’, J. Funct. Anal. 254(2) (2008), 368–395.CrossRefGoogle Scholar
Chung, J., Guo, Z., Kwon, S. and Oh, T., ‘Normal form approach to global well-posedness of the quadratic derivative Schrödinger equation on the circle’, Ann. Inst. H. Poincaré Anal. Non Linéaire 34 (2017), 1273–1297.Google Scholar
Colliander, J., Keel, M., Staffilani, G., Takaoka, H. and Tao, T., ‘A refined global well-posedness result for Schrödinger equations with derivative’, SIAM J. Math. Anal. 34(1) (2002), 64–86.Google Scholar
Colliander, J., Keel, M., Staffilani, G., Takaoka, H. and Tao, T., ‘Sharp global well-posedness for KdV and modified KdV on ℝ and T’, J. Amer. Math. Soc. 16(3) (2003), 705–749.Google Scholar
Colliander, J., Keel, M., Staffilani, G., Takaoka, H. and Tao, T., ‘Multilinear estimates for periodic KdV equations, and applications’, J. Funct. Anal. 211(1) (2004), 173–218.Google Scholar
Colliander, J. and Oh, T., ‘Almost sure well-posedness of the periodic cubic nonlinear Schrödinger equation below L 2(T)’, Duke Math. J. 161(3) (2012), 367–414.Google Scholar
Fibich, G., Ilan, B. and Papanicolaou, G., ‘Self-focusing with fourth-order dispersion’, SIAM J. Appl. Math. 62(4) (2002), 1437–1462.Google Scholar
Guo, Z., ‘Local well-posedness and a priori bounds for the modified Benjamin–Ono equation’, Adv. Differential Equations 16(11–12) (2011), 1087–1137.Google Scholar
Guo, Z., Kwon, S. and Oh, T., ‘Poincaré–Dulac normal form reduction for unconditional well-posedness of the periodic cubic NLS’, Comm. Math. Phys. 322(1) (2013), 19–48.Google Scholar
Guo, Z. and Oh, T., ‘Non-existence of solutions for the periodic cubic NLS below L 2 ’, Int. Math. Res. Not. IMRN (6) (2018), 1656–1729.Google Scholar
Hardy, G. H. and Wright, E. M., An Introduction to the Theory of Numbers, 5th edn (The Clarendon Press, Oxford University Press, New York, 1979), xvi+426 pp.Google Scholar
Ionescu, A., Kenig, C. and Tataru, D., ‘Global well-posedness of the KP-I initial-value problem in the energy space’, Invent. Math. 173(2) (2008), 265–304.Google Scholar
Ivanov, B. A. and Kosevich, A. M., ‘Stable three-dimensional small-amplitude soliton in magnetic materials’, So. J. Low Temp. Phys. 9 (1983), 439–442.Google Scholar
Karpman, V. I., ‘Stabilization of soliton instabilities by higher-order dispersion: fourth order nonlinear Schrödinger-type equations’, Phys. Rev. E 53(2) (1996), 1336–1339.Google Scholar
Karpman, V. I. and Shagalov, A. G., ‘Solitons and their stability in high dispersive systems. I. Fourth-order nonlinear Schrödinger-type equations with power-law nonlinearities’, Phys. Lett. A 228(1–2) (1997), 59–65.CrossRefGoogle Scholar
Kenig, C. and Pilod, D., ‘Well-posedness for the fifth-order KdV equation in the energy space’, Trans. Amer. Math. Soc. 367(4) (2015), 2551–2612.CrossRefGoogle Scholar
Koch, H. and Tataru, D., ‘ A priori bounds for the 1D cubic NLS in negative Sobolev spaces’, Int. Math. Res. Not. IMRN 2007(16), Art. ID rnm053, 36 pp.Google Scholar
Koch, H. and Tataru, D., ‘Energy and local energy bounds for the 1-d cubic NLS equation in H -1/4 ’, Ann. Inst. H. Poincaré Anal. Non Linéaire 29(6) (2012), 955–988.Google Scholar
Koch, H. and Tzvetkov, N., ‘On the local well-posedness of the Benjamin–Ono equation in H s (ℝ)’, Int. Math. Res. Not. IMRN 2003(26) (2003), 1449–1464.Google Scholar
Kwak, C., ‘Periodic fourth-order cubic NLS: Local well-posedness and Non-squeezing property’, J. Math. Anal. Appl. 461(2) (2018), 1327–1364.CrossRefGoogle Scholar
Miyaji, T. and Tsutsumi, Y., ‘Local well-posedness of the NLS equation with third order dispersion in negative Sobolev spaces’, Differential Integral Equations 31(1–2) (2018), 111–132.CrossRefGoogle Scholar
Molinet, L., Pilod, D. and Vento, S., ‘On unconditional well-posedness for the periodic modified Korteweg–de Vries equation’, J. Math. Soc. Japan, to appear.Google Scholar
Nakanishi, K., Takaoka, H. and Tsutsumi, Y., ‘Local well-posedness in low regularity of the mKdV equation with periodic boundary condition’, Discrete Contin. Dyn. Syst. 28(4) (2010), 1635–1654.Google Scholar
Oh, T., Sosoe, P. and Tzvetkov, N., ‘An optimal regularity result on the quasi-invariant Gaussian measures for the cubic fourth order nonlinear Schrödinger equation’, Preprint, 2017, arXiv:1707.01666 [math.AP].CrossRefGoogle Scholar
Oh, T. and Sulem, C., ‘On the one-dimensional cubic nonlinear Schrödinger equation below L 2 ’, Kyoto J. Math. 52(1) (2012), 99–115.Google Scholar
Oh, T. and Thomann, L., ‘A pedestrian approach to the invariant Gibbs measure for the 2-d defocusing nonlinear Schrödinger equations’, Stoch. Partial Differ. Equ. Anal. Comput. (2018) https://doi.org/10.1007/s40072-018-0112-2.Google Scholar
Oh, T. and Tzvetkov, N., ‘Quasi-invariant Gaussian measures for the cubic fourth order nonlinear Schrödinger equation’, Probab. Theory Related Fields 169 (2017), 1121–1168.Google Scholar
Oh, T., Tzvetkov, N. and Wang, Y., Solving the 4NLS with white noise initial data, Preprint.Google Scholar
Oh, T. and Wang, Y., ‘On the ill-posedness of the cubic nonlinear Schrödinger equation on the circle’, An. Ştiinţ. Univ. Al. I. Cuza Iaşi. Mat. (N.S.), to appear.Google Scholar
Takaoka, H. and Tsutsumi, Y., ‘Well-posedness of the Cauchy problem for the modified KdV equation with periodic boundary condition’, Int. Math. Res. Not. IMRN 2004(56) (2004), 3009–3040.Google Scholar
Turitsyn, S. K., ‘Three-dimensional dispersion of nonlinearity and stability of multidimensional solitons’, Teoret. Mat. Fiz. 64 (1985), 226–232 (in Russian).Google Scholar