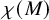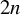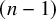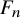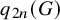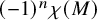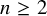1 Introduction
In this paper, we address the following problem: if M denotes a closed, orientable even-dimensional manifold with a given fundamental group G, then what restriction does this impose on the Euler characteristic of M? In the particular case when
![]() $\chi (M)=2$
, we have the related problem of determining which finite groups can be the fundamental group of a closed, topological,
$\chi (M)=2$
, we have the related problem of determining which finite groups can be the fundamental group of a closed, topological,
![]() $2n$
-manifold M with the rational homology of the
$2n$
-manifold M with the rational homology of the
![]() $2n$
-sphere (see previous work on the
$2n$
-sphere (see previous work on the
![]() $4$
-dimensional case by Hambleton-Kreck [Reference Hambleton and Kreck13] and Teichner [Reference Teichner43]). We introduce the following invariant for discrete groups, extending a definition due to Hausmann and Weinberger [Reference Hausmann and Weinberger19] for 4–manifolds:
$4$
-dimensional case by Hambleton-Kreck [Reference Hambleton and Kreck13] and Teichner [Reference Teichner43]). We introduce the following invariant for discrete groups, extending a definition due to Hausmann and Weinberger [Reference Hausmann and Weinberger19] for 4–manifolds:
Definition 1.1. Given a finitely presented group G, define
![]() $q_{2n}(G)$
as the minimum value of
$q_{2n}(G)$
as the minimum value of
![]() $(-1)^n\chi (M)$
for a closed, orientable
$(-1)^n\chi (M)$
for a closed, orientable
![]() $2n$
-manifold M with
$2n$
-manifold M with
![]() $(n-1)$
-connected universal cover, such that
$(n-1)$
-connected universal cover, such that
![]() $\pi _1(M)=G$
.
$\pi _1(M)=G$
.
We will first assume that G is a finite group. Recall that Swan [Reference Swan42, p. 193] defined an invariant
![]() $\mu _k(G)$
, for each
$\mu _k(G)$
, for each
![]() $k \geq 1$
, by the condition that
$k \geq 1$
, by the condition that
![]() $(-1)^k|G|\mu _k (G)$
is the minimal value over all partial Euler characteristics of a free resolution of
$(-1)^k|G|\mu _k (G)$
is the minimal value over all partial Euler characteristics of a free resolution of
![]() $\mathbb Z$
truncated after degree k. We call this a k-step resolution. However, since projective
$\mathbb Z$
truncated after degree k. We call this a k-step resolution. However, since projective
![]() $\mathbb Z G$
-modules are locally free [Reference Swan40, Section 8], k-step projective resolutions can be used instead to define
$\mathbb Z G$
-modules are locally free [Reference Swan40, Section 8], k-step projective resolutions can be used instead to define
![]() $\mu ^{\prime }_k(G) \leq \mu _k(G)$
(see [Reference Swan42, Remark, p. 195]).
$\mu ^{\prime }_k(G) \leq \mu _k(G)$
(see [Reference Swan42, Remark, p. 195]).
Let
![]() $e_n(G)$
denote the least integer greater than or equal to all the numbers
$e_n(G)$
denote the least integer greater than or equal to all the numbers
where the coefficients range over
![]() $\mathbb F = \mathbb Q$
or
$\mathbb F = \mathbb Q$
or
![]() $\mathbb F = \mathbb F_p$
for all primes p. Our main result is the following:
$\mathbb F = \mathbb F_p$
for all primes p. Our main result is the following:
Theorem A. If G is a finite group and
![]() $n \geq 2$
, then
$n \geq 2$
, then
Remark 1.2. By [Reference Swan42, Theorem 5.1],
![]() $\mu ^{\prime }_k(G) = \mu _k(G)$
unless G has periodic cohomology of (necessarily even) period dividing
$\mu ^{\prime }_k(G) = \mu _k(G)$
unless G has periodic cohomology of (necessarily even) period dividing
![]() $k+1$
, and G admits no periodic free resolution of period
$k+1$
, and G admits no periodic free resolution of period
![]() $k+1$
. In this case,
$k+1$
. In this case,
![]() $k\geq 3$
is odd, and we will say that the pair
$k\geq 3$
is odd, and we will say that the pair
![]() $(G,k)$
is exceptional (see Remark 2.8). For example,
$(G,k)$
is exceptional (see Remark 2.8). For example,
![]() $\mu ^{\prime }_3(G) < \mu _3(G)$
for some of the
$\mu ^{\prime }_3(G) < \mu _3(G)$
for some of the
![]() $4$
-periodic groups
$4$
-periodic groups
![]() $G = Q(8p,q)$
in Milnor’s list (see the calculations in [Reference Madsen29, Reference Milgram31]). If
$G = Q(8p,q)$
in Milnor’s list (see the calculations in [Reference Madsen29, Reference Milgram31]). If
![]() $(G,n)$
is an exceptional pair, we provide information about
$(G,n)$
is an exceptional pair, we provide information about
![]() $q_{2n}(G)$
in Theorem B and Remark 3.13 below.
$q_{2n}(G)$
in Theorem B and Remark 3.13 below.
The invariants
![]() $e_n(G)$
and the
$e_n(G)$
and the
![]() $\mu _k(G)$
, for
$\mu _k(G)$
, for
![]() $1\leq k \leq n$
, can also be defined for infinite discrete groups of type
$1\leq k \leq n$
, can also be defined for infinite discrete groups of type
![]() $F_n$
, meaning that there is a model for
$F_n$
, meaning that there is a model for
![]() $K(G,1)$
with finite n-skeleton. In this case, we obtain similar estimates with a slightly weaker lower bound. Recall that a finitely presented group G is said to be good if topological surgery with fundamental group G holds in dimension four (see Freedman-Quinn [Reference Freedman and Quinn9, p. 99]).
$K(G,1)$
with finite n-skeleton. In this case, we obtain similar estimates with a slightly weaker lower bound. Recall that a finitely presented group G is said to be good if topological surgery with fundamental group G holds in dimension four (see Freedman-Quinn [Reference Freedman and Quinn9, p. 99]).
Theorem A′. If G is an infinite discrete group of type
![]() $F_n$
with
$F_n$
with
![]() $n\geq 2$
, then
$n\geq 2$
, then
If
![]() $n \geq 3$
, or
$n \geq 3$
, or
![]() $n=2$
and G is good, then
$n=2$
and G is good, then
![]() $q_{2n}(G)\le 2 \mu _{n}(G)$
.
$q_{2n}(G)\le 2 \mu _{n}(G)$
.
The invariants
![]() $\mu ^{\prime \prime }_k(G) = \mu _k(G)$
, for
$\mu ^{\prime \prime }_k(G) = \mu _k(G)$
, for
![]() $k \geq 3$
, and we define
$k \geq 3$
, and we define
![]() $\mu ^{\prime \prime }_2(G) = 1 - \operatorname {\mathrm {Def}}(G)$
, and
$\mu ^{\prime \prime }_2(G) = 1 - \operatorname {\mathrm {Def}}(G)$
, and
![]() $\mu ^{\prime \prime }_1(G) = d(G) -1$
, where
$\mu ^{\prime \prime }_1(G) = d(G) -1$
, where
![]() $\operatorname {\mathrm {Def}}(G)$
is the deficiency of G, defined as the maximum difference
$\operatorname {\mathrm {Def}}(G)$
is the deficiency of G, defined as the maximum difference
![]() $d-r$
of numbers of generators minus relations over all finite presentations of G (see [Reference Epstein8]) and
$d-r$
of numbers of generators minus relations over all finite presentations of G (see [Reference Epstein8]) and
![]() $d(G)$
denotes the minimal number of generators for G. These modifications to the previous invariants arise from the additional condition that the resolutions be geometrically realisable (see Section 4). For
$d(G)$
denotes the minimal number of generators for G. These modifications to the previous invariants arise from the additional condition that the resolutions be geometrically realisable (see Section 4). For
![]() $k=2$
, determining the relation between
$k=2$
, determining the relation between
![]() $\mu _2(G)$
and
$\mu _2(G)$
and
![]() $1-\operatorname {\mathrm {Def}}(G)$
is part of Wall’s (unsolved) D2 problem [Reference Wall45, Section 2], which for infinite groups is related to the Eilenberg-Ganea conjecture [Reference Eilenberg and Ganea7].
$1-\operatorname {\mathrm {Def}}(G)$
is part of Wall’s (unsolved) D2 problem [Reference Wall45, Section 2], which for infinite groups is related to the Eilenberg-Ganea conjecture [Reference Eilenberg and Ganea7].
Our results sharpen and generalise the estimate proved by Hausmann-Weinberger [Reference Hausmann and Weinberger19, Théorème 1]:
since
![]() $\mu _2(G) \leq (1- \operatorname {\mathrm {Def}}(G))$
by [Reference Swan42, Proposition 1]. The results of Kirk-Livingston [Reference Kirk and Livingston23] for
$\mu _2(G) \leq (1- \operatorname {\mathrm {Def}}(G))$
by [Reference Swan42, Proposition 1]. The results of Kirk-Livingston [Reference Kirk and Livingston23] for
![]() $q_4(\mathbb Z^n)$
show that these bounds can be improved for specific groups.
$q_4(\mathbb Z^n)$
show that these bounds can be improved for specific groups.
The proof of the lower bound in Theorem A for
![]() $q_{2n}(G)$
is given in Section 2. In Section 3, we establish the upper bound
$q_{2n}(G)$
is given in Section 2. In Section 3, we establish the upper bound
![]() $q_{2n}(G) \leq 2\mu _n(G)$
by generalising the well-known “thickening” construction for groups G which admit a balanced presentation with equal numbers of generators and relations (i.e.,
$q_{2n}(G) \leq 2\mu _n(G)$
by generalising the well-known “thickening” construction for groups G which admit a balanced presentation with equal numbers of generators and relations (i.e.,
![]() $\operatorname {\mathrm {Def}}(G) =0$
). For
$\operatorname {\mathrm {Def}}(G) =0$
). For
![]() $n=2$
, this involves showing that finite D2-complex es with good fundamental groups (e.g., groups of finite order) admit suitable thickenings via methods from topological surgery (see Theorem 3.8).
$n=2$
, this involves showing that finite D2-complex es with good fundamental groups (e.g., groups of finite order) admit suitable thickenings via methods from topological surgery (see Theorem 3.8).
Example 1.3. For
![]() $E_k=(\mathbb Z/p\mathbb Z)^k$
, an elementary abelian p-group,
$E_k=(\mathbb Z/p\mathbb Z)^k$
, an elementary abelian p-group,
![]() $e_n(E_k)=\mu _n(E_k)-\mu _{n-1}(E_k)$
, and this number can be explicitly computed using the Kunneth formula (see Example 3.14). This can be used to show that
$e_n(E_k)=\mu _n(E_k)-\mu _{n-1}(E_k)$
, and this number can be explicitly computed using the Kunneth formula (see Example 3.14). This can be used to show that
![]() $q_{2n}(E_k)$
grows like a polynomial of degree n in k, for example
$q_{2n}(E_k)$
grows like a polynomial of degree n in k, for example
For n even,
![]() $q_{2n}(G)\ge 2$
, as the minimal possible Euler characteristic that can occur in our setting is
$q_{2n}(G)\ge 2$
, as the minimal possible Euler characteristic that can occur in our setting is
![]() $\chi (M) = 2$
, which holds when M has the rational homology of a
$\chi (M) = 2$
, which holds when M has the rational homology of a
![]() $2n$
-sphere, and is implied by Theorem A if
$2n$
-sphere, and is implied by Theorem A if
![]() $\mu _n(G) =1$
. The condition
$\mu _n(G) =1$
. The condition
![]() $\mu _2(G) = 1$
also holds for groups of deficiency zero, and there are many groups with this property (see [Reference Wamsley51]). In contrast, our computations for the groups
$\mu _2(G) = 1$
also holds for groups of deficiency zero, and there are many groups with this property (see [Reference Wamsley51]). In contrast, our computations for the groups
![]() $E_k=(\mathbb Z/p\mathbb Z)^k$
show that
$E_k=(\mathbb Z/p\mathbb Z)^k$
show that
![]() $q_{4n}(E_k)>2$
for all
$q_{4n}(E_k)>2$
for all
![]() $n>1$
and
$n>1$
and
![]() $k\ge 3$
. Hence, higher dimensional rational homology spheres with elementary abelian fundamental group of rank larger than 2 cannot occur.
$k\ge 3$
. Hence, higher dimensional rational homology spheres with elementary abelian fundamental group of rank larger than 2 cannot occur.
For periodic groups, we can compute
![]() $q_{2n}(G)$
in certain cases, which, in particular, provides an alternate argument for [Reference Hambleton and Kreck13, Corollary 4.4] and generalises that result to higher dimensions:
$q_{2n}(G)$
in certain cases, which, in particular, provides an alternate argument for [Reference Hambleton and Kreck13, Corollary 4.4] and generalises that result to higher dimensions:
Theorem B. Let G be a finite periodic group of (even) period q. Then
![]() $q_{2n}(G) = 2$
if q divides
$q_{2n}(G) = 2$
if q divides
![]() $n+2$
, and
$n+2$
, and
![]() $q_{2n}(G) = 0$
if
$q_{2n}(G) = 0$
if
![]() $2q$
divides
$2q$
divides
![]() $n+1$
.
$n+1$
.
Remark 1.4. Note that in our setting,
![]() $\chi (M)>0$
if and only if n is even (see Corollary 2.13). Thus, for n odd, the minimal possible value of
$\chi (M)>0$
if and only if n is even (see Corollary 2.13). Thus, for n odd, the minimal possible value of
![]() $q_{2n}(G)= - \chi (M)$
is zero. Apart from the results of Theorem B for periodic groups with twice their period dividing
$q_{2n}(G)= - \chi (M)$
is zero. Apart from the results of Theorem B for periodic groups with twice their period dividing
![]() $n+1$
, any finite group G which acts freely and homologically trivially on some product
$n+1$
, any finite group G which acts freely and homologically trivially on some product
![]() $S^n \times S^n$
will have
$S^n \times S^n$
will have
![]() $q_{2n}(G) = 0$
. There are many such examples, including any products
$q_{2n}(G) = 0$
. There are many such examples, including any products
![]() $G = G_1 \times G_2$
of periodic groups, many rank two finite p-groups, including the extra-special p-groups of order
$G = G_1 \times G_2$
of periodic groups, many rank two finite p-groups, including the extra-special p-groups of order
![]() $p^3$
, and all the finite odd order subgroups of the exceptional Lie group
$p^3$
, and all the finite odd order subgroups of the exceptional Lie group
![]() $G_2$
(see [Reference Hambleton11, Reference Hambleton and Ünlü17, Reference Hambleton and Ünlü18]).
$G_2$
(see [Reference Hambleton11, Reference Hambleton and Ünlü17, Reference Hambleton and Ünlü18]).
We are especially interested in the case of rational homology
![]() $4$
-spheres (called
$4$
-spheres (called
![]() $\mathbb Q S^4$
manifolds) with finite fundamental group. In Section 5, we consider the following “inverse” problem, for which the lower bound implies significant restrictions on G.
$\mathbb Q S^4$
manifolds) with finite fundamental group. In Section 5, we consider the following “inverse” problem, for which the lower bound implies significant restrictions on G.
Question. Which finite groups can be the fundamental group of a closed, topological,
![]() $4$
-manifold M with the rational homology of the
$4$
-manifold M with the rational homology of the
![]() $4$
-sphere?
$4$
-sphere?
For example, it was observed in [Reference Hambleton and Kreck13, p. 100] that if G is finite abelian, then
![]() $d(G) \leq 3$
(see Corollary 5.1). This bound follows directly by estimating the Hausmann-Weinberger invariant
$d(G) \leq 3$
(see Corollary 5.1). This bound follows directly by estimating the Hausmann-Weinberger invariant
![]() $q_4(G)$
. Moreover, Teichner [Reference Teichner43, Section 4.13] showed that this bound is best possible for abelian groups by explicit construction of examples.
$q_4(G)$
. Moreover, Teichner [Reference Teichner43, Section 4.13] showed that this bound is best possible for abelian groups by explicit construction of examples.
Our methods shed light on more complicated finite groups by making use of cohomology with twisted coefficients to obtain better lower bounds for
![]() $q_4(G)$
:
$q_4(G)$
:
Theorem C. Let
![]() $U_k=E_k\times _T C$
, where p is an odd prime,
$U_k=E_k\times _T C$
, where p is an odd prime,
![]() $E_k=(\mathbb Z/pZ)^k$
, and C cyclic of order prime to p acts on each
$E_k=(\mathbb Z/pZ)^k$
, and C cyclic of order prime to p acts on each
![]() $\mathbb Z/p\mathbb Z$
factor in
$\mathbb Z/p\mathbb Z$
factor in
![]() $E_k$
via
$E_k$
via
![]() $x\mapsto x^q$
, where q is a unit in
$x\mapsto x^q$
, where q is a unit in
![]() $\mathbb Z/p\mathbb Z$
.
$\mathbb Z/p\mathbb Z$
.
-
(i) If
 $x^{q^2}\ne x$
for all
$x^{q^2}\ne x$
for all
 $1\ne x\in E_k$
, then for all
$1\ne x\in E_k$
, then for all
 $k>4$
,
$k>4$
,
 $U_k$
does not arise as the fundamental group of any rational homology 4–sphere.
$U_k$
does not arise as the fundamental group of any rational homology 4–sphere. -
(ii) If
 $q=p-1$
, then for all
$q=p-1$
, then for all
 $k>1$
,
$k>1$
,
 $U_k$
does not arise as the fundamental group of any rational homology 4–sphere.
$U_k$
does not arise as the fundamental group of any rational homology 4–sphere.
This paper is organised as follows: in Section 2, we analyse free group actions on
![]() $(n-1)$
-connected
$(n-1)$
-connected
![]() $2n$
-manifolds using cohomological methods; in Section 3, we discuss minimal complexes and thickenings; in Section 4, we prove Theorem A
$2n$
-manifolds using cohomological methods; in Section 3, we discuss minimal complexes and thickenings; in Section 4, we prove Theorem A
![]() $'$
; in Section 5, we focus on rational homology 4–spheres; and in Section 6, we collect some remarks, examples, and questions related to the invariants introduced here. Appendix A contains the proof of Theorem 3.8.
$'$
; in Section 5, we focus on rational homology 4–spheres; and in Section 6, we collect some remarks, examples, and questions related to the invariants introduced here. Appendix A contains the proof of Theorem 3.8.
2 Free actions on
 $(n-1)$
-connected
$(n-1)$
-connected
 $2n$
-manifolds
$2n$
-manifolds
In this section, we will apply the cohomological approach outlined in [Reference Adem and Hambleton1, Section 2]. The proofs of Propositions 2.1, 2.3, and 2.5 are straightforward modifications of the results there and details are omitted. We assume that Y is a closed, orientable,
![]() $(n-1)$
-connected
$(n-1)$
-connected
![]() $2n$
-manifold with the free orientation-preserving action of a finite group G; its homology has a corresponding
$2n$
-manifold with the free orientation-preserving action of a finite group G; its homology has a corresponding
![]() $\mathbb Z G$
–module structure. Both
$\mathbb Z G$
–module structure. Both
![]() $H_{2n}(Y,\mathbb Z)$
and
$H_{2n}(Y,\mathbb Z)$
and
![]() $H_0(Y,\mathbb Z)$
are copies of the trivial module
$H_0(Y,\mathbb Z)$
are copies of the trivial module
![]() $\mathbb Z$
, whereas
$\mathbb Z$
, whereas
![]() $H_n(Y,\mathbb Z)$
is a free abelian group with a
$H_n(Y,\mathbb Z)$
is a free abelian group with a
![]() $\mathbb Z G$
–module structure which, by Poincaré duality, must be self–dual as a
$\mathbb Z G$
–module structure which, by Poincaré duality, must be self–dual as a
![]() $\mathbb Z G$
–module, that is,
$\mathbb Z G$
–module, that is,
![]() $H_n(Y,\mathbb Z)\cong H_n(Y,\mathbb Z)^*$
. We assume, here, that Y admits a finite G–CW complex structure, with cellular chain complex denoted by
$H_n(Y,\mathbb Z)\cong H_n(Y,\mathbb Z)^*$
. We assume, here, that Y admits a finite G–CW complex structure, with cellular chain complex denoted by
![]() $C_*(Y)$
(if the action is smooth, this is always true, and holds up to G-homotopy equivalence in the topological case).
$C_*(Y)$
(if the action is smooth, this is always true, and holds up to G-homotopy equivalence in the topological case).
We denote by
![]() $\Omega ^r(\mathbb Z )$
the
$\Omega ^r(\mathbb Z )$
the
![]() $ \mathbb Z G$
-module uniquely defined in the stable category (where
$ \mathbb Z G$
-module uniquely defined in the stable category (where
![]() $\mathbb Z G$
-modules are identified up to stabilisation by projectives) as the r–fold dimension–shift of the trivial module
$\mathbb Z G$
-modules are identified up to stabilisation by projectives) as the r–fold dimension–shift of the trivial module
![]() $\mathbb Z$
. We refer to [Reference Adem and Milgram2] and [Reference Brown3] for background on group cohomology.
$\mathbb Z$
. We refer to [Reference Adem and Milgram2] and [Reference Brown3] for background on group cohomology.
Proposition 2.1. Let Y be an
![]() $(n-1)$
-connected
$(n-1)$
-connected
![]() $2n$
-manifold with a free action of a finite group G which preserves orientation. Then there is a short exact sequence in the stable category of
$2n$
-manifold with a free action of a finite group G which preserves orientation. Then there is a short exact sequence in the stable category of
![]() $\mathbb Z G$
–modules of the form
$\mathbb Z G$
–modules of the form
Corollary 2.2. The short exact sequence (2.1) yields a long exact sequence in Tate cohomology
determined by the class
![]() $\sigma \in \widehat H^{-2n-1}(G,\mathbb Z)$
which is the image of the generator
$\sigma \in \widehat H^{-2n-1}(G,\mathbb Z)$
which is the image of the generator
![]() $ 1\in \widehat H^{0}(G,\mathbb Z)\cong \mathbb Z/|G|$
.
$ 1\in \widehat H^{0}(G,\mathbb Z)\cong \mathbb Z/|G|$
.
We can analyse this sequence just as was done in [Reference Adem and Hambleton1, Section 2].
Proposition 2.3. The cohomology class
![]() $\sigma \in \widehat H^{-2n-1}(G,\mathbb Z) \cong H_{2n}(G,\mathbb Z)$
can be identified with the image of the fundamental class
$\sigma \in \widehat H^{-2n-1}(G,\mathbb Z) \cong H_{2n}(G,\mathbb Z)$
can be identified with the image of the fundamental class
![]() $c_*[Y/G]$
under the homomorphism
$c_*[Y/G]$
under the homomorphism
induced by the classifying map
![]() $c\colon Y/G\to BG$
. Under this identification, the class
$c\colon Y/G\to BG$
. Under this identification, the class
![]() $\sigma $
determines the extension (2.1).
$\sigma $
determines the extension (2.1).
Remark 2.4. This property of the extension class was proved for
![]() $n=2$
in [Reference Hambleton and Kreck13, Corollary 2.4], and the proof in the general case is similar.
$n=2$
in [Reference Hambleton and Kreck13, Corollary 2.4], and the proof in the general case is similar.
Similarly, the map
![]() $\Omega ^{n+1}(\mathbb Z)\to H_n(Y,\mathbb Z)$
defines an extension class
$\Omega ^{n+1}(\mathbb Z)\to H_n(Y,\mathbb Z)$
defines an extension class
which appears in the long exact sequence above as the image of the generator under the map
![]() $\widehat H^0(G,\mathbb Z)\to \widehat H^{n+1}(G,\mathbb Z)$
. Algebraically, this responds to mapping the canonical defining extension for
$\widehat H^0(G,\mathbb Z)\to \widehat H^{n+1}(G,\mathbb Z)$
. Algebraically, this responds to mapping the canonical defining extension for
![]() $\Omega ^{n+1}(\mathbb Z)$
(identified with the extension class for the module of cycles in
$\Omega ^{n+1}(\mathbb Z)$
(identified with the extension class for the module of cycles in
![]() $C_n(Y)$
) to the extension obtained by reducing by the module of boundaries
$C_n(Y)$
) to the extension obtained by reducing by the module of boundaries
![]() $B_n$
:
$B_n$
:

These two extension classes are related as follows:
Proposition 2.5. Let G denote a finite group acting freely on an
![]() $(n-1)$
-connected, orientable
$(n-1)$
-connected, orientable
![]() $2n$
-manifold Y preserving orientation, then
$2n$
-manifold Y preserving orientation, then
![]() $\varepsilon _Y\ne 0$
and
$\varepsilon _Y\ne 0$
and
![]() $|G| = \textrm {exp} (\sigma )\cdot \textrm {exp} (\varepsilon _Y)$
. The class
$|G| = \textrm {exp} (\sigma )\cdot \textrm {exp} (\varepsilon _Y)$
. The class
![]() $\varepsilon _Y$
has exponent
$\varepsilon _Y$
has exponent
![]() $|G|$
if and only if
$|G|$
if and only if
![]() $\sigma =0$
, in which case, we have a stable equivalence
$\sigma =0$
, in which case, we have a stable equivalence
Example 2.6. Observing that the cohomology of a group with periodic cohomology is always zero in odd dimensions, we see that if G has periodic cohomology, then there is a stable equivalence
![]() $H_n(Y,\mathbb Z)\cong \Omega ^{n+1}(\mathbb Z)\oplus \Omega ^{-n-1}(\mathbb Z)$
.
$H_n(Y,\mathbb Z)\cong \Omega ^{n+1}(\mathbb Z)\oplus \Omega ^{-n-1}(\mathbb Z)$
.
We note the standard identity
![]() $\chi (Y) = 2 + (-1)^n\dim H_n(Y,\mathbb Q)$
, and the formula
$\chi (Y) = 2 + (-1)^n\dim H_n(Y,\mathbb Q)$
, and the formula
![]() $|G|\chi (Y/G) = \chi (Y)$
from the covering
$|G|\chi (Y/G) = \chi (Y)$
from the covering
![]() $Y \to Y/G$
. Since the transfer map induces an isomorphism
$Y \to Y/G$
. Since the transfer map induces an isomorphism
![]() $H_i(Y/G;\mathbb Q) \cong H_i(Y;\mathbb Q)^G$
, we have
$H_i(Y/G;\mathbb Q) \cong H_i(Y;\mathbb Q)^G$
, we have
![]() $\chi (Y/G) = 2 + (-1)^n\dim H_n(Y, \mathbb Q)^G$
. In particular
$\chi (Y/G) = 2 + (-1)^n\dim H_n(Y, \mathbb Q)^G$
. In particular
From the stable sequence
we infer the existence of projective modules
![]() $Q_r$
and
$Q_r$
and
![]() $Q_s$
which fit into an exact sequence
$Q_s$
which fit into an exact sequence
where
![]() $Q_i \otimes \mathbb Q \cong [\mathbb Q G]^i$
for
$Q_i \otimes \mathbb Q \cong [\mathbb Q G]^i$
for
![]() $i=r,s$
. Here, we write
$i=r,s$
. Here, we write
![]() $\Omega ^{j+1}(\mathbb Z)$
(
$\Omega ^{j+1}(\mathbb Z)$
(
![]() $j\geq 0$
) for the j-th kernel in a minimal projective resolution of
$j\geq 0$
) for the j-th kernel in a minimal projective resolution of
![]() $\mathbb Z$
, meaning a resolution:
$\mathbb Z$
, meaning a resolution:
realising
![]() $\mu ^{\prime }_j(G)$
(see [Reference Swan42, p. 193]), from which we see that
$\mu ^{\prime }_j(G)$
(see [Reference Swan42, p. 193]), from which we see that
where
![]() $(-1)^k|G|\mu ^{\prime }_k (G)$
is precisely the minimal value over all partial Euler characteristics of a projective resolution of
$(-1)^k|G|\mu ^{\prime }_k (G)$
is precisely the minimal value over all partial Euler characteristics of a projective resolution of
![]() $\mathbb Z$
over
$\mathbb Z$
over
![]() $\mathbb Z G$
(see [Reference Swan42, Remark, p. 195]). The corresponding invariants
$\mathbb Z G$
(see [Reference Swan42, Remark, p. 195]). The corresponding invariants
![]() $\mu _k(G)$
for minimal free resolutions of
$\mu _k(G)$
for minimal free resolutions of
![]() $\mathbb Z$
were defined by Swan (see [Reference Swan42, p. 193]).
$\mathbb Z$
were defined by Swan (see [Reference Swan42, p. 193]).
By dualising, we see that a minimal representative for
![]() $\Omega ^{-j}(\mathbb Z)$
is given by
$\Omega ^{-j}(\mathbb Z)$
is given by
![]() $\Omega ^j(\mathbb Z)^*$
, the dual module. Thus, for our purposes, we have
$\Omega ^j(\mathbb Z)^*$
, the dual module. Thus, for our purposes, we have
Applying invariants after tensoring over
![]() $\mathbb Q$
to the exact sequence (2.2) yields the formula
$\mathbb Q$
to the exact sequence (2.2) yields the formula
whence we obtain
Theorem 2.7. If Y is a closed,
![]() $(n-1)$
-connected
$(n-1)$
-connected
![]() $2n$
-manifold with a free orientation-preserving action of G, a finite group, then for any subgroup
$2n$
-manifold with a free orientation-preserving action of G, a finite group, then for any subgroup
![]() $H\subset G$
$H\subset G$
Proof. We will prove this for
![]() $H=G$
by contradiction. Assume that
$H=G$
by contradiction. Assume that
![]() $s-r>0$
and form the diagram
$s-r>0$
and form the diagram

where L is the quotient of
![]() $\Omega ^{n+1}(\mathbb Z) \oplus Q_r$
in the middle vertical exact sequence. Note that this middle vertical exact sequence splits (since L is torsion-free). Hence,
$\Omega ^{n+1}(\mathbb Z) \oplus Q_r$
in the middle vertical exact sequence. Note that this middle vertical exact sequence splits (since L is torsion-free). Hence,
By Swan [Reference Swan41, Lemma 2.1], there is a projective resolution
Since
![]() $s>r$
, this contradicts the minimality of the resolution (2.3) realising
$s>r$
, this contradicts the minimality of the resolution (2.3) realising
![]() $\mu ^{\prime }_n(G)$
. Hence, we have shown that
$\mu ^{\prime }_n(G)$
. Hence, we have shown that
![]() $s-r\le 0$
. The full result follows using covering spaces.
$s-r\le 0$
. The full result follows using covering spaces.
Remark 2.8. As mentioned in the Introduction, Swan proved that
![]() $\mu ^{\prime }_k(G) = \mu _k(G)$
unless G has periodic cohomology of period dividing
$\mu ^{\prime }_k(G) = \mu _k(G)$
unless G has periodic cohomology of period dividing
![]() $k+1$
, and G admits no periodic free resolution of period
$k+1$
, and G admits no periodic free resolution of period
![]() $k+1$
. In these exceptional cases,
$k+1$
. In these exceptional cases,
![]() $\mu _k (G) = 1$
and
$\mu _k (G) = 1$
and
![]() $\mu ^{\prime }_k(G) = 0$
. In contrast,
$\mu ^{\prime }_k(G) = 0$
. In contrast,
![]() $\mu _k (G) = 0$
if G has a periodic free resolution of period
$\mu _k (G) = 0$
if G has a periodic free resolution of period
![]() $k + 1$
and
$k + 1$
and
![]() $G\ne 1$
. We also note that if the pair
$G\ne 1$
. We also note that if the pair
![]() $(G,k)$
is exceptional, then
$(G,k)$
is exceptional, then
![]() $k\geq 3$
is odd and G is noncyclic. In particular,
$k\geq 3$
is odd and G is noncyclic. In particular,
![]() $\mu ^{\prime }_k(G) = \mu _k(G)$
if G is a finite p-group (see [Reference Swan42, Corollary 5.2]).
$\mu ^{\prime }_k(G) = \mu _k(G)$
if G is a finite p-group (see [Reference Swan42, Corollary 5.2]).
If the pair
![]() $(G,n)$
is not exceptional, the numbers
$(G,n)$
is not exceptional, the numbers
![]() $\mu _n(G)$
can be computed using group cohomology. By a result of Swan [Reference Swan42, Proposition 6.1], the invariant
$\mu _n(G)$
can be computed using group cohomology. By a result of Swan [Reference Swan42, Proposition 6.1], the invariant
![]() $\mu _n(G)$
is the least integer greater than or equal to all the numbers
$\mu _n(G)$
is the least integer greater than or equal to all the numbers
as M ranges over all simple
![]() $\mathbb F_pG$
–modules for all primes p dividing
$\mathbb F_pG$
–modules for all primes p dividing
![]() $|G|$
. As extending the field doesn’t change dimensions, we can take
$|G|$
. As extending the field doesn’t change dimensions, we can take
![]() $\mathbb K_p$
, an algebraically closed field of characteristic p, and restrict attention to absolutely irreducible
$\mathbb K_p$
, an algebraically closed field of characteristic p, and restrict attention to absolutely irreducible
![]() $\mathbb K_pG$
–modules. Next we introduce
$\mathbb K_pG$
–modules. Next we introduce
Definition 2.9. For any discrete group G of type
![]() $F_n$
, let
$F_n$
, let
![]() $e_n(G)$
denote the least integer greater than or equal to all the numbers
$e_n(G)$
denote the least integer greater than or equal to all the numbers
where the coefficients range over
![]() $\mathbb F = \mathbb Q$
or
$\mathbb F = \mathbb Q$
or
![]() $\mathbb F = \mathbb F_p$
for all primes p.
$\mathbb F = \mathbb F_p$
for all primes p.
Remark 2.10. When
![]() $G=P$
is a finite p–group, the trivial module
$G=P$
is a finite p–group, the trivial module
![]() $\mathbb F_p$
is the only simple module, and we can verify that
$\mathbb F_p$
is the only simple module, and we can verify that
![]() $\mu _n (P)-\mu _{n-1}(P) = e_n(P)$
.
$\mu _n (P)-\mu _{n-1}(P) = e_n(P)$
.
We have the following elementary inequality:
Lemma 2.11. Suppose that X is a closed, orientable
![]() $2n$
-manifold with fundamental group G of type
$2n$
-manifold with fundamental group G of type
![]() $F_n$
whose universal cover is
$F_n$
whose universal cover is
![]() $(n-1)$
-connected. Then, for any subgroup
$(n-1)$
-connected. Then, for any subgroup
![]() $H\subset G$
of finite index
$H\subset G$
of finite index
Proof. Let
![]() $\mathbb F$
denote any field of coefficients. The connectivity of the universal cover implies that
$\mathbb F$
denote any field of coefficients. The connectivity of the universal cover implies that
and
By Poincaré duality, we have
Combining these facts and using covering space theory, we obtain the inequality.
Applying the mod p coefficient sequence yields an attractive corollary
Corollary 2.12. If X is a closed, orientable
![]() $2n$
-manifold with finite fundamental group G whose universal cover is
$2n$
-manifold with finite fundamental group G whose universal cover is
![]() $(n-1)$
-connected, then for all primes p dividing
$(n-1)$
-connected, then for all primes p dividing
![]() $|G|$
and subgroups
$|G|$
and subgroups
![]() $H\subset G$
$H\subset G$
Proof. Since
![]() $[G:H]\chi (X)$
equals the Euler characteristic of the
$[G:H]\chi (X)$
equals the Euler characteristic of the
![]() $[G:H]$
-fold covering of X, it is enough to do the case
$[G:H]$
-fold covering of X, it is enough to do the case
![]() $H=G$
. Let
$H=G$
. Let
![]() $h^i(G) = \dim H^i(G;\mathbb F_p)$
. From the relations noted above, and Lemma 2.11, we have the formula
$h^i(G) = \dim H^i(G;\mathbb F_p)$
. From the relations noted above, and Lemma 2.11, we have the formula
 $$ \begin{align*}(-1)^n(\chi(X) -2) \geq h^n(G) - 2\sum_{i =1}^{n-1} (-1)^{i+1} h^{n-i}(G).\end{align*} $$
$$ \begin{align*}(-1)^n(\chi(X) -2) \geq h^n(G) - 2\sum_{i =1}^{n-1} (-1)^{i+1} h^{n-i}(G).\end{align*} $$
But by the mod p coefficient sequence, we have
The result follows by combining these two relations.
Applying this to any subgroup
![]() $C\subset G$
of prime order, we obtain
$C\subset G$
of prime order, we obtain
Corollary 2.13. If X is a closed, orientable
![]() $2n$
-manifold with
$2n$
-manifold with
![]() $(n-1)$
-connected universal cover and nontrivial finite fundamental group G, then
$(n-1)$
-connected universal cover and nontrivial finite fundamental group G, then
![]() $\chi (X)>0$
if and only if n is even.
$\chi (X)>0$
if and only if n is even.
Proof. Let
![]() $C\subset G$
be a cyclic subgroup of order p, a prime. Then
$C\subset G$
be a cyclic subgroup of order p, a prime. Then
![]() $H^{2k}(C;\mathbb Z) = \mathbb Z/p\mathbb Z$
(if
$H^{2k}(C;\mathbb Z) = \mathbb Z/p\mathbb Z$
(if
![]() $k>0$
), and
$k>0$
), and
![]() $H^{2k+1}(C;\mathbb Z) = 0$
. For n even, applying the inequality above with
$H^{2k+1}(C;\mathbb Z) = 0$
. For n even, applying the inequality above with
![]() $H = C$
yields
$H = C$
yields
![]() $\chi (X)>0$
. When n is odd, note that
$\chi (X)>0$
. When n is odd, note that
![]() $b_n(X) \neq 0$
implies
$b_n(X) \neq 0$
implies
![]() $b_n(X) \geq 2$
, since the intersection form of X is nonsingular and skew-symmetric. Hence,
$b_n(X) \geq 2$
, since the intersection form of X is nonsingular and skew-symmetric. Hence,
![]() $\chi (X)\le 0$
.
$\chi (X)\le 0$
.
3 Minimal
 $K(G,n)$
-complexes and thickenings
$K(G,n)$
-complexes and thickenings
We now turn our attention to the existence of orientable
![]() $2n$
-manifolds having fundamental group of type
$2n$
-manifolds having fundamental group of type
![]() $F_n$
and
$F_n$
and
![]() $(n-1)$
-connected universal cover. We recall the following well-known construction (see Kreck and Schafer [Reference Kreck and Schafer24, Section 2]):
$(n-1)$
-connected universal cover. We recall the following well-known construction (see Kreck and Schafer [Reference Kreck and Schafer24, Section 2]):
Proposition 3.1. Let G be a discrete group of type
![]() $F_n$
for
$F_n$
for
![]() $n\ge 2$
. Then there exists a closed, orientable
$n\ge 2$
. Then there exists a closed, orientable
![]() $2n$
-manifold Z, such that
$2n$
-manifold Z, such that
![]() $\pi _1(Z) =G$
with
$\pi _1(Z) =G$
with
![]() $(n-1)$
-connected universal cover.
$(n-1)$
-connected universal cover.
Proof. Let K denote a finite CW complex of dimension n with
![]() $\pi _1(K) = G$
whose universal covering is
$\pi _1(K) = G$
whose universal covering is
![]() $(n-1)$
-connected. For example, take a finite, cellular model for the classifying space
$(n-1)$
-connected. For example, take a finite, cellular model for the classifying space
![]() $BG$
, and consider its n-skeleton K. Then we can construct a smooth
$BG$
, and consider its n-skeleton K. Then we can construct a smooth
![]() $2n$
-manifold
$2n$
-manifold
![]() $Z=M(K)$
by doubling a
$Z=M(K)$
by doubling a
![]() $2n$
-dimensional handlebody thickening of K. Thus, the universal cover
$2n$
-dimensional handlebody thickening of K. Thus, the universal cover
![]() $\tilde {Z}$
of
$\tilde {Z}$
of
![]() $M(K)$
is an
$M(K)$
is an
![]() $(n-1)$
-connected, closed, orientable
$(n-1)$
-connected, closed, orientable
![]() $2n$
-manifold with a free action of G, such that
$2n$
-manifold with a free action of G, such that
where
![]() $\Lambda := \mathbb Z G$
denotes the integral group ring. Moreover, the Euler characteristic
$\Lambda := \mathbb Z G$
denotes the integral group ring. Moreover, the Euler characteristic
![]() $\chi (M(K)) = 2 \chi (K)$
. A variation of this construction is to let Z denote the boundary of a regular neigbourhood, for some embedding
$\chi (M(K)) = 2 \chi (K)$
. A variation of this construction is to let Z denote the boundary of a regular neigbourhood, for some embedding
![]() $K \subset \mathbb R^{2n+1}$
of the finite n-complex in Euclidean space.
$K \subset \mathbb R^{2n+1}$
of the finite n-complex in Euclidean space.
Definition 3.2. Let G be a discrete group of type
![]() $F_n$
. A finite CW complex K of dimension
$F_n$
. A finite CW complex K of dimension
![]() $n\geq 2$
, with fundamental group
$n\geq 2$
, with fundamental group
![]() $\pi _1(K) = G$
and
$\pi _1(K) = G$
and
![]() $\pi _i(K) =0$
for
$\pi _i(K) =0$
for
![]() $1\leq i \leq n-1$
, is called a
$1\leq i \leq n-1$
, is called a
![]() $K(G,n)$
-complex.
$K(G,n)$
-complex.
The chain complex
![]() $C_*(\tilde {K})$
of the universal covering of a
$C_*(\tilde {K})$
of the universal covering of a
![]() $K(G,n)$
-complex affords a free n-step resolution of the trivial
$K(G,n)$
-complex affords a free n-step resolution of the trivial
![]() $\mathbb Z G$
–module
$\mathbb Z G$
–module
![]() $\mathbb Z$
. Conversely, we wish to realise a given finitely generated n-step free resolution
$\mathbb Z$
. Conversely, we wish to realise a given finitely generated n-step free resolution
as the equivariant chain complex of a suitable
![]() $K(G,n)$
-complex. Note that by Swan [Reference Swan42, Theorem 1.2], we have
$K(G,n)$
-complex. Note that by Swan [Reference Swan42, Theorem 1.2], we have
![]() $\mu _n(G) \leq (-1)^n\chi (\mathscr F)$
and that the lower bound is attained by some resolution.
$\mu _n(G) \leq (-1)^n\chi (\mathscr F)$
and that the lower bound is attained by some resolution.
Proposition 3.3. Let G be a discrete group of type
![]() $F_n$
, and let
$F_n$
, and let
![]() $\mathscr F$
be an n-step resolution of
$\mathscr F$
be an n-step resolution of
![]() $\mathbb Z$
by finitely generated free
$\mathbb Z$
by finitely generated free
![]() $ZG$
-modules. If
$ZG$
-modules. If
![]() $n \geq 3$
, then there exists a finite
$n \geq 3$
, then there exists a finite
![]() $K(G,n)$
-complex K and a G-equivariant chain homotopy equivalence
$K(G,n)$
-complex K and a G-equivariant chain homotopy equivalence
![]() $C_*(\widetilde K) \simeq \mathscr F $
.
$C_*(\widetilde K) \simeq \mathscr F $
.
Proof. Let
![]() $n \geq 3$
, we can apply [Reference Hambleton, Pamuk and Yalçın16, Lemma 8.12] to show that
$n \geq 3$
, we can apply [Reference Hambleton, Pamuk and Yalçın16, Lemma 8.12] to show that
![]() $\mathscr F$
is chain homotopy-equivalent to a finitely generated free complex
$\mathscr F$
is chain homotopy-equivalent to a finitely generated free complex
![]() $\mathscr F'$
which agrees with the
$\mathscr F'$
which agrees with the
![]() $2$
-skeleton of a model for
$2$
-skeleton of a model for
![]() $K(G,1)$
. Then the construction of [Reference Swan41, Lemma 3.1] (credited to Milnor) provides the required complex K by successively attaching i-cells equivariantly using the boundary maps from the chain complex
$K(G,1)$
. Then the construction of [Reference Swan41, Lemma 3.1] (credited to Milnor) provides the required complex K by successively attaching i-cells equivariantly using the boundary maps from the chain complex
![]() $\mathscr F'$
.
$\mathscr F'$
.
Remark 3.4. For finite groups, Swan [Reference Swan42, Corollary 5.1] shows that under certain additional assumptions, one can geometrically realise the actual sequence
![]() $f_0, f_1, f_2, \dots $
of ranks for the i-chains of
$f_0, f_1, f_2, \dots $
of ranks for the i-chains of
![]() $\mathscr F$
. We also record the facts due to Swan that
$\mathscr F$
. We also record the facts due to Swan that
![]() $\mu _n(G) \geq 1$
for n even, and
$\mu _n(G) \geq 1$
for n even, and
![]() $\mu _n(G) \geq 0$
for n odd if
$\mu _n(G) \geq 0$
for n odd if
![]() $G \neq 1$
is finite (see [Reference Swan42, Section 1]).
$G \neq 1$
is finite (see [Reference Swan42, Section 1]).
Corollary 3.5. If
![]() $n \geq 3$
, then for any discrete group of type
$n \geq 3$
, then for any discrete group of type
![]() $F_n$
, we have
$F_n$
, we have
![]() $q_{2n}(G) \leq 2\mu _n(G)$
. In particular, if n is even and G is a finite group with
$q_{2n}(G) \leq 2\mu _n(G)$
. In particular, if n is even and G is a finite group with
![]() $\mu _n(G) =1$
, then G is the fundamental group of a rational homology
$\mu _n(G) =1$
, then G is the fundamental group of a rational homology
![]() $2n$
-sphere.
$2n$
-sphere.
Proof. We apply Proposition 3.3 to a minimal n-step resolution
![]() $\mathscr F$
with
$\mathscr F$
with
![]() $\chi (\mathscr F) =\mu _n(G)$
, and obtain a finite
$\chi (\mathscr F) =\mu _n(G)$
, and obtain a finite
![]() $K(G,n)$
-complex K. The manifold
$K(G,n)$
-complex K. The manifold
![]() $Z= M(K)$
constructed in Proposition 3.1 provides the upper bound
$Z= M(K)$
constructed in Proposition 3.1 provides the upper bound
![]() $q_{2n}(G) \leq \chi (Z) = 2 \mu _n(G)$
.
$q_{2n}(G) \leq \chi (Z) = 2 \mu _n(G)$
.
We now consider the case
![]() $n=2$
, where the argument above fails at the first step. To establish our upper bound for
$n=2$
, where the argument above fails at the first step. To establish our upper bound for
![]() $q_4(G)$
, we need a more general construction and some results of C. T. C. Wall [Reference Wall45, Reference Wall46].
$q_4(G)$
, we need a more general construction and some results of C. T. C. Wall [Reference Wall45, Reference Wall46].
Definition 3.6. A finite complex X satisfies Wall’s
![]() $\mathrm {D2}$
-conditions if
$\mathrm {D2}$
-conditions if
![]() $H_i(\widetilde X) =0$
, for
$H_i(\widetilde X) =0$
, for
![]() $i>2$
, and
$i>2$
, and
![]() $H^{3}(X; \mathcal B) = 0$
, for all coefficient bundles
$H^{3}(X; \mathcal B) = 0$
, for all coefficient bundles
![]() $\mathcal B$
. Here,
$\mathcal B$
. Here,
![]() $\widetilde X$
denotes the universal covering of X. If these conditions hold, we will say that X is a
$\widetilde X$
denotes the universal covering of X. If these conditions hold, we will say that X is a
![]() $\mathrm {D2}$
-complex. If every
$\mathrm {D2}$
-complex. If every
![]() $\mathrm {D2}$
-complex with fundamental group G is homotopy-equivalent to a finite
$\mathrm {D2}$
-complex with fundamental group G is homotopy-equivalent to a finite
![]() $2$
-complex, then we say that G has the
$2$
-complex, then we say that G has the
![]() $\mathrm {D2}$
-property.
$\mathrm {D2}$
-property.
In [Reference Wall45, p. 64], Wall proved that a finite complex X satisfying the D2-conditions is homotopy-equivalent to a finite
![]() $3$
-complex. We will therefore assume that all our D2-complexes have
$3$
-complex. We will therefore assume that all our D2-complexes have
![]() $\dim X \leq 3$
. It is not known at present whether all discrete groups have the D2-property. Note that
$\dim X \leq 3$
. It is not known at present whether all discrete groups have the D2-property. Note that
![]() $\mu _2(G) \leq (1- \operatorname {\mathrm {Def}}(G))$
by [Reference Swan42, Proposition 1], and equality holds if G has the D2-property.
$\mu _2(G) \leq (1- \operatorname {\mathrm {Def}}(G))$
by [Reference Swan42, Proposition 1], and equality holds if G has the D2-property.
Proposition 3.7 [Reference Hambleton12, Corollary 2.4]
Any finitely generated free resolution
over
![]() $\mathbb Z G$
is chain homotopy-equivalent to
$\mathbb Z G$
is chain homotopy-equivalent to
![]() $C_*(X)$
, where X is a finite
$C_*(X)$
, where X is a finite
![]() $\mathrm {D2}$
-complex.
$\mathrm {D2}$
-complex.
If we apply this to a minimal resolution with
![]() $\chi (\mathscr F) = \mu _2(G) = \mu ^{\prime }_2(G)$
, then if G is finite, the module
$\chi (\mathscr F) = \mu _2(G) = \mu ^{\prime }_2(G)$
, then if G is finite, the module
![]() $H_2(\widetilde X;\mathbb Z)$
is a minimal
$H_2(\widetilde X;\mathbb Z)$
is a minimal
![]() $\mathbb Z$
-rank representative of the stable module
$\mathbb Z$
-rank representative of the stable module
![]() $\Omega ^3(\mathbb Z)$
. The following result may also be of independent interest (it applies to any finitely presented group G which is good in the sense of Freedman [Reference Freedman and Quinn9, p. 99], in particular, to poly-(finite or cyclic) groups).
$\Omega ^3(\mathbb Z)$
. The following result may also be of independent interest (it applies to any finitely presented group G which is good in the sense of Freedman [Reference Freedman and Quinn9, p. 99], in particular, to poly-(finite or cyclic) groups).
Theorem 3.8. For any finite
![]() $\mathrm {D2}$
-complex X with good fundamental group, there exists a closed, topological
$\mathrm {D2}$
-complex X with good fundamental group, there exists a closed, topological
![]() $4$
-manifold
$4$
-manifold
![]() $M(X)$
with
$M(X)$
with
![]() $\pi _1(M(X)) = \pi _1(X)$
and
$\pi _1(M(X)) = \pi _1(X)$
and
![]() $\chi (M(X)) = 2\chi (X)$
.
$\chi (M(X)) = 2\chi (X)$
.
For continuity, we defer the proof of this result to Appendix A.
Corollary 3.9. For G a finitely presented good group,
![]() $q_{4}(G) \leq 2\mu _2(G)$
. In particular,
$q_{4}(G) \leq 2\mu _2(G)$
. In particular,
![]() $\mu _2(G) =1$
and G finite implies that G is the fundamental group of a rational homology
$\mu _2(G) =1$
and G finite implies that G is the fundamental group of a rational homology
![]() $4$
-sphere.
$4$
-sphere.
Proof. We apply Proposition 3.7 to realise a minimal
![]() $2$
-step resolution by a finite
$2$
-step resolution by a finite
![]() $\mathrm {D2}$
-complex, and then Theorem 3.8 provides a suitable
$\mathrm {D2}$
-complex, and then Theorem 3.8 provides a suitable
![]() $\mathbb Q S^4$
manifold.
$\mathbb Q S^4$
manifold.
The proof of Theorem A
Concatenating our previous results, we have obtained the estimates
for any finite group G. For the lower bound, we apply Theorem 2.7 and Lemma 2.11. For the upper bound, we apply Corollary 3.5 if
![]() $n>2$
, and Corollary 3.9 for
$n>2$
, and Corollary 3.9 for
![]() $n=2$
.
$n=2$
.
We now prepare for the proof of Theorem B. The next result, due to Swan and Wall, shows that arbitrary periodic groups appear as fundamental groups of rational homology spheres.
Lemma 3.10. If G is a finite group with periodic cohomology of period dividing
![]() $2k+2$
, then
$2k+2$
, then
![]() $\mu _{2k}(G) =1$
for
$\mu _{2k}(G) =1$
for
![]() $k \geq 1$
.
$k \geq 1$
.
Proof. We will discuss the case
![]() $k=1$
for groups of period
$k=1$
for groups of period
![]() $4$
. Swan [Reference Swan41] constructed a finitely dominated Poincaré
$4$
. Swan [Reference Swan41] constructed a finitely dominated Poincaré
![]() $3$
-complex Y with
$3$
-complex Y with
![]() $\pi _1(Y) = G$
, and Wall [Reference Wall47, Corollary 2.3.2] shows that Y is obtained from a
$\pi _1(Y) = G$
, and Wall [Reference Wall47, Corollary 2.3.2] shows that Y is obtained from a
![]() $\mathrm {D2}$
-complex by attaching a single
$\mathrm {D2}$
-complex by attaching a single
![]() $3$
-cell. The chain complex
$3$
-cell. The chain complex
![]() $C_*(\widetilde Y)$
provides a projective resolution
$C_*(\widetilde Y)$
provides a projective resolution
with
![]() $\chi (\mathscr F') =1$
, where P is projective,
$\chi (\mathscr F') =1$
, where P is projective,
![]() $F_1$
and
$F_1$
and
![]() $F_0$
are free and
$F_0$
are free and
![]() $I(G)^* =\ker d_2(\mathscr F')$
. This shows that
$I(G)^* =\ker d_2(\mathscr F')$
. This shows that
![]() $\mu ^{\prime }_2(G) =1$
and so
$\mu ^{\prime }_2(G) =1$
and so
![]() $\mu _2(G) = \mu ^{\prime }_2(G) =1$
by Swan’s results.
$\mu _2(G) = \mu ^{\prime }_2(G) =1$
by Swan’s results.
One can give a direct argument for this last step. By adding a projective Q so that
![]() $P\oplus Q = F$
is free, we obtain a free resolution
$P\oplus Q = F$
is free, we obtain a free resolution
with
![]() $I(G)^* \oplus Q = \ker d_2(\mathscr F)$
. By the ‘Roiter replacement lemma’ (see [Reference Roĭter36, Proposition 5], or [Reference Jacobinski21, Theorem 3.6]),
$I(G)^* \oplus Q = \ker d_2(\mathscr F)$
. By the ‘Roiter replacement lemma’ (see [Reference Roĭter36, Proposition 5], or [Reference Jacobinski21, Theorem 3.6]),
![]() $I(G)^* \oplus Q = J \oplus F'$
, where
$I(G)^* \oplus Q = J \oplus F'$
, where
![]() $F'$
is free and J is locally isomorphic to
$F'$
is free and J is locally isomorphic to
![]() $I(G)^*$
, so
$I(G)^*$
, so
![]() $\operatorname {\mathrm {rank}}_{\mathbb Z} (J) = \operatorname {\mathrm {rank}}_{\mathbb Z}I(G)^*$
. We now divide out the image of
$\operatorname {\mathrm {rank}}_{\mathbb Z} (J) = \operatorname {\mathrm {rank}}_{\mathbb Z}I(G)^*$
. We now divide out the image of
![]() $F'$
in F (a direct summand) to obtain a free resolution
$F'$
in F (a direct summand) to obtain a free resolution
with
![]() $J =\ker d_2(\mathscr F'')$
and
$J =\ker d_2(\mathscr F'')$
and
![]() $\chi (\mathscr F'') =1$
. Hence,
$\chi (\mathscr F'') =1$
. Hence,
![]() $\mu _2(G) = 1$
.
$\mu _2(G) = 1$
.
A similar argument shows that
![]() $\mu _{2k}(G) =1$
, for all
$\mu _{2k}(G) =1$
, for all
![]() $k>1$
, if G has periodic cohomology with period dividing
$k>1$
, if G has periodic cohomology with period dividing
![]() $2k+2$
. Details will be left to the reader.
$2k+2$
. Details will be left to the reader.
Remark 3.11. The calculation in Lemma 3.10 together with Theorem 3.8 provides an alternate proof of [Reference Hambleton and Kreck13, Corollary 4.4]. However, the essential ingredients are the same in both arguments.
The proof of Theorem B
By assumption, the group G is periodic of even period q. In the first case, if q divides
![]() $n+2$
, then n is even and
$n+2$
, then n is even and
![]() $\mu _n(G) =1$
by Lemma 3.10. By Theorem A, we have the inequalities
$\mu _n(G) =1$
by Lemma 3.10. By Theorem A, we have the inequalities
and hence,
![]() $q_{2n}(G) =2$
.
$q_{2n}(G) =2$
.
In the second case, n is odd and the minimal Euler characteristic
![]() $q_{2n}(G)\geq 0$
by Corollary 2.13. We will show that the lower bound is realised when G is a periodic group of even period q, provided that
$q_{2n}(G)\geq 0$
by Corollary 2.13. We will show that the lower bound is realised when G is a periodic group of even period q, provided that
![]() $2q$
divides
$2q$
divides
![]() $n+1$
.
$n+1$
.
This follows from the solution of the space form problem: Madsen, Thomas and Wall [Reference Madsen, Thomas and Wall28, Theorem 1], [Reference Wall49, Corollary 12.6] proved that there exists a finite Poincaré duality complex X (called a finite Swan complex) of dimension
![]() $(2k-1)$
, with
$(2k-1)$
, with
![]() $\pi _1(X) = G$
and universal covering
$\pi _1(X) = G$
and universal covering
![]() $\widetilde X \simeq S^{2k-1}$
, whenever
$\widetilde X \simeq S^{2k-1}$
, whenever
![]() $k \equiv 0 \ \pmod { e(G)}$
, where
$k \equiv 0 \ \pmod { e(G)}$
, where
![]() $e(G)$
is the Artin exponent of G [Reference Lam25, p. 94]. Moreover, a detailed analysis of the group cohomology of periodic groups shows that
$e(G)$
is the Artin exponent of G [Reference Lam25, p. 94]. Moreover, a detailed analysis of the group cohomology of periodic groups shows that
![]() $2e(G)$
is equal to q or
$2e(G)$
is equal to q or
![]() $2q$
, depending on the structure of its
$2q$
, depending on the structure of its
![]() $2$
-hyperelementary subgroups (see Wall [Reference Wall49, p. 542], where the notation
$2$
-hyperelementary subgroups (see Wall [Reference Wall49, p. 542], where the notation
![]() $2d(\pi )$
is used for the period of a periodic group
$2d(\pi )$
is used for the period of a periodic group
![]() $\pi $
).
$\pi $
).
For any finite Swan complex X, there exists a degree one normal map
![]() $(f, b)\colon N \to X$
, where
$(f, b)\colon N \to X$
, where
![]() $N^{n}$
is a closed, topological n-manifold (see [Reference Thomas and Wall44, Corollary 3.3]). We then have a degree one normal map of pairs
$N^{n}$
is a closed, topological n-manifold (see [Reference Thomas and Wall44, Corollary 3.3]). We then have a degree one normal map of pairs
By Wall’s ‘
![]() $\pi $
-
$\pi $
-
![]() $\pi $
Theorem’ [Reference Wall and Ranicki50, Theorem 3.3], this normal map is normally cobordant to a homotopy equivalence of pairs. It follows that
$\pi $
Theorem’ [Reference Wall and Ranicki50, Theorem 3.3], this normal map is normally cobordant to a homotopy equivalence of pairs. It follows that
![]() $X \times S^n$
is homotopy-equivalent to a closed, topological
$X \times S^n$
is homotopy-equivalent to a closed, topological
![]() $2n$
-manifold. Since
$2n$
-manifold. Since
![]() $X \times S^n$
has Euler characteristic zero, these examples show that
$X \times S^n$
has Euler characteristic zero, these examples show that
![]() $q_{2n}(G) = 0$
as required.
$q_{2n}(G) = 0$
as required.
Remark 3.12 (Smooth examples)
If G satisfies the
![]() $2p$
-conditions (meaning that every subgroup of order
$2p$
-conditions (meaning that every subgroup of order
![]() $2p$
is cyclic, for p prime), Madsen, Thomas and Wall [Reference Madsen, Thomas and Wall28, Theorem 5] proved that there exists a closed, oriented, smooth
$2p$
is cyclic, for p prime), Madsen, Thomas and Wall [Reference Madsen, Thomas and Wall28, Theorem 5] proved that there exists a closed, oriented, smooth
![]() $(2k-1)$
-manifold
$(2k-1)$
-manifold
![]() $N^{2k-1}$
with
$N^{2k-1}$
with
![]() $\pi _1(N) = G$
and universal covering
$\pi _1(N) = G$
and universal covering
![]() $\widetilde N = S^{2k-1}$
, whenever
$\widetilde N = S^{2k-1}$
, whenever
![]() $k \equiv 0 \ \pmod { e(G)}$
. Under this extra assumption, the products
$k \equiv 0 \ \pmod { e(G)}$
. Under this extra assumption, the products
![]() $N^n \times S^{n}$
, for
$N^n \times S^{n}$
, for
![]() $n = 2qr-1$
, provide smooth manifolds realising the minimum value
$n = 2qr-1$
, provide smooth manifolds realising the minimum value
![]() $q_{2n}(G) = 0$
.
$q_{2n}(G) = 0$
.
Remark 3.13 (The exceptional case)
In the arguments above, we have not used the full strength of the Madsen-Thomas-Wall results, which produce smooth space forms in the minimal dimension
![]() $q-1$
whenever
$q-1$
whenever
![]() $q= 2e(G)$
(see the discussion on [Reference Madsen, Thomas and Wall28, p. 142]). This observation does give additional examples of periodic groups with
$q= 2e(G)$
(see the discussion on [Reference Madsen, Thomas and Wall28, p. 142]). This observation does give additional examples of periodic groups with
![]() $q_{2n}(G) = 0$
, for example, when
$q_{2n}(G) = 0$
, for example, when
![]() $n+1 \equiv 2 \ \pmod {4}$
, but deciding whether
$n+1 \equiv 2 \ \pmod {4}$
, but deciding whether
![]() $2e(G)$
equals q or
$2e(G)$
equals q or
![]() $2q$
for a given G involves difficult number theory.
$2q$
for a given G involves difficult number theory.
If the pair
![]() $(G. n)$
is exceptional, then surgery theory can be used to study
$(G. n)$
is exceptional, then surgery theory can be used to study
![]() $q_{2n}(G)$
as follows (see [Reference Madsen, Thomas and Wall27, Sections 2–3] for background on the space form problem):
$q_{2n}(G)$
as follows (see [Reference Madsen, Thomas and Wall27, Sections 2–3] for background on the space form problem):
-
(i) For any periodic group with period
 $n+1$
, there exists a finitely dominated Swan complex X with
$n+1$
, there exists a finitely dominated Swan complex X with
 $\pi _1(X) = G$
and universal covering
$\pi _1(X) = G$
and universal covering
 $\widetilde X \simeq S^n$
(see [Reference Swan41, Proposition 3.1]).
$\widetilde X \simeq S^n$
(see [Reference Swan41, Proposition 3.1]). -
(ii) For any finitely dominated Swan complex X, there exists a degree one normal map
 $(f, b)\colon N \to X$
, where
$(f, b)\colon N \to X$
, where
 $N^{n}$
is a closed, oriented, topological n-manifold (see [Reference Thomas and Wall44, Corollary 3.3] and [Reference Wall48, Proposition 2]).
$N^{n}$
is a closed, oriented, topological n-manifold (see [Reference Thomas and Wall44, Corollary 3.3] and [Reference Wall48, Proposition 2]). -
(iii) The product
 $X \times S^n$
is homotopy-equivalent to a finite Poincaré complex (by the product formula for Wall’s finiteness obstruction [Reference Gersten10, Theorem 0.1]).
$X \times S^n$
is homotopy-equivalent to a finite Poincaré complex (by the product formula for Wall’s finiteness obstruction [Reference Gersten10, Theorem 0.1]). -
(iv) We have a degree one normal map
with surgery obstruction $$ \begin{align*}(f\times \mathrm{id}, b\times \mathrm{id})\colon N \times S^n \to X \times S^n,\end{align*} $$
$$ \begin{align*}(f\times \mathrm{id}, b\times \mathrm{id})\colon N \times S^n \to X \times S^n,\end{align*} $$
 $\lambda (f,b) \in L^h_{2n}(\mathbb Z G)$
determined by the Wall finiteness obstruction
$\lambda (f,b) \in L^h_{2n}(\mathbb Z G)$
determined by the Wall finiteness obstruction
 $\sigma (X) \in \widetilde K_0(\mathbb Z G)$
(see [Reference Pedersen and Ranicki34, p. 244]).
$\sigma (X) \in \widetilde K_0(\mathbb Z G)$
(see [Reference Pedersen and Ranicki34, p. 244]).
-
(v) If
 $\lambda (f,b) = 0$
(this is the hard step), then this normal map would be normally cobordant to a homotopy equivalence. In other words,
$\lambda (f,b) = 0$
(this is the hard step), then this normal map would be normally cobordant to a homotopy equivalence. In other words,
 $X \times S^n$
would be homotopy-equivalent to a closed, topological
$X \times S^n$
would be homotopy-equivalent to a closed, topological
 $2n$
-manifold with Euler characteristic zero.
$2n$
-manifold with Euler characteristic zero.
We conclude this section with a sample computation of the estimates for elementary abelian p-groups.
Example 3.14. If
![]() $E_k=(\mathbb Z/p\mathbb Z)^k$
then we can use the Kunneth formula to compute these invariants. The term
$E_k=(\mathbb Z/p\mathbb Z)^k$
then we can use the Kunneth formula to compute these invariants. The term
![]() $\mu _n(E_k)$
has a polynomial of degree n as its leading term. For
$\mu _n(E_k)$
has a polynomial of degree n as its leading term. For
![]() $n=2, 3, 4$
, we have
$n=2, 3, 4$
, we have
For instance, for
![]() $k=2$
, this only gives the rough estimate
$k=2$
, this only gives the rough estimate
![]() $1\leq q_8(E_2) \leq 6$
, but we know that
$1\leq q_8(E_2) \leq 6$
, but we know that
![]() $q_8(E_2) =2$
by performing surgeryFootnote
1
on
$q_8(E_2) =2$
by performing surgeryFootnote
1
on
![]() $L^7(\mathbb Z/p\mathbb Z) \times S^1$
. However, for
$L^7(\mathbb Z/p\mathbb Z) \times S^1$
. However, for
![]() $k=3$
, the lower bound gives
$k=3$
, the lower bound gives
![]() $q_8(E_3) \geq 3$
, and hence,
$q_8(E_3) \geq 3$
, and hence,
![]() $E_3$
is not the fundamental group of a rational homology
$E_3$
is not the fundamental group of a rational homology
![]() $8$
-sphere.
$8$
-sphere.
4 The proof of Theorem A′
In this section, we establish a lower bound for
![]() $q_{2n}(G)$
, for G an infinite discrete group of type
$q_{2n}(G)$
, for G an infinite discrete group of type
![]() $F_n$
. With the results of Lemma 2.11, Corollary 3.5 and Corollary 3.9, this will complete the proof of Theorem A
$F_n$
. With the results of Lemma 2.11, Corollary 3.5 and Corollary 3.9, this will complete the proof of Theorem A
![]() $'$
.
$'$
.
The invariants
![]() $\mu ^{\prime \prime }_k(G)$
used in the statement of Theorem A
$\mu ^{\prime \prime }_k(G)$
used in the statement of Theorem A
![]() $'$
can also be defined as follows.
$'$
can also be defined as follows.
Definition 4.1. For
![]() $k \geq 2$
, let
$k \geq 2$
, let
![]() $\mu ^{\prime \prime }_{k}(G)=(-1)^k \cdot \min \{\chi (\mathscr F)\}$
, where
$\mu ^{\prime \prime }_{k}(G)=(-1)^k \cdot \min \{\chi (\mathscr F)\}$
, where
![]() $\mathscr F$
varies over all k-step resolutions
$\mathscr F$
varies over all k-step resolutions
of
![]() $\mathbb Z$
by finitely generated free
$\mathbb Z$
by finitely generated free
![]() $\mathbb Z G$
-modules, which arise geometrically as the chain complex of the universal covering for a finite
$\mathbb Z G$
-modules, which arise geometrically as the chain complex of the universal covering for a finite
![]() $CW$
-complex of dimension k with fundamental group G.
$CW$
-complex of dimension k with fundamental group G.
The sign
![]() $(-1)^k$
is introduced to agree with Swan’s conventions. Note the inequalities
$(-1)^k$
is introduced to agree with Swan’s conventions. Note the inequalities
relating these invariants to those defined by Swan. We define
![]() $\mu ^{\prime \prime }_1(G) = d(G) -1$
, where
$\mu ^{\prime \prime }_1(G) = d(G) -1$
, where
![]() $d(G)$
denotes the minimal number of generators for G.
$d(G)$
denotes the minimal number of generators for G.
Remark 4.2. By Proposition 3.3, we have
![]() $\mu _k(G) = \mu ^{\prime \prime }_k(G)$
if
$\mu _k(G) = \mu ^{\prime \prime }_k(G)$
if
![]() $n\geq 3$
. Note that
$n\geq 3$
. Note that
![]() $\mu ^{\prime \prime }_2(G) = 1- \operatorname {\mathrm {Def}}(G)$
. If
$\mu ^{\prime \prime }_2(G) = 1- \operatorname {\mathrm {Def}}(G)$
. If
![]() $\mu _2(G) < \mu ^{\prime \prime }_2(G)$
for some finitely presented group G, then there would be a counter-example to Wall’s D2 problem (but no such examples are known at present). In addition, we do not know if the strict inequality
$\mu _2(G) < \mu ^{\prime \prime }_2(G)$
for some finitely presented group G, then there would be a counter-example to Wall’s D2 problem (but no such examples are known at present). In addition, we do not know if the strict inequality
![]() $\mu _1(G) < d(G) -1$
can occur.
$\mu _1(G) < d(G) -1$
can occur.
We now establish the lower bound for infinite groups.
Theorem 4.3. Let G be a discrete group of type
![]() $F_n$
, for
$F_n$
, for
![]() $n\geq 2$
. If Y is a closed,
$n\geq 2$
. If Y is a closed,
![]() $(n-1)$
-connected
$(n-1)$
-connected
![]() $2n$
-manifold with a free orientation-preserving action of G, a finite group, then for any subgroup
$2n$
-manifold with a free orientation-preserving action of G, a finite group, then for any subgroup
![]() $H\subset G$
of finite index
$H\subset G$
of finite index
Proof. It suffices to prove this inequality for
![]() $H = G$
, and then apply covering space theory. Let M denote a closed, orientable,
$H = G$
, and then apply covering space theory. Let M denote a closed, orientable,
![]() $2n$
-dimensional manifold with
$2n$
-dimensional manifold with
![]() $n \geq 2$
and fundamental group G of type
$n \geq 2$
and fundamental group G of type
![]() $F_n$
, such that
$F_n$
, such that
![]() $\pi _i(M) = 0 $
for
$\pi _i(M) = 0 $
for
![]() $1 < i <n$
. Let
$1 < i <n$
. Let
![]() $K \simeq M$
be a finite
$K \simeq M$
be a finite
![]() $CW$
-complex homotopy-equivalent to M, and let
$CW$
-complex homotopy-equivalent to M, and let
![]() $C:= C(K; \Lambda ) = C(\widetilde K)$
denote the chain complex of its universal covering. It is a finite chain complex, with each
$C:= C(K; \Lambda ) = C(\widetilde K)$
denote the chain complex of its universal covering. It is a finite chain complex, with each
![]() $C_i$
a finitely generated free
$C_i$
a finitely generated free
![]() $\mathbb Z G$
-module. We note that the homology of M is computed from the chain complex
$\mathbb Z G$
-module. We note that the homology of M is computed from the chain complex
![]() $C \otimes _{\mathbb Z G}\mathbb Z$
, and therefore,
$C \otimes _{\mathbb Z G}\mathbb Z$
, and therefore,
![]() $\chi (M) = \sum _{i=0}^{2n} (-1)^i c_i$
, where
$\chi (M) = \sum _{i=0}^{2n} (-1)^i c_i$
, where
![]() $c_i := \operatorname {\mathrm {rank}}_{\mathbb Z G} C_i$
.
$c_i := \operatorname {\mathrm {rank}}_{\mathbb Z G} C_i$
.
We may assume that the
![]() $(n-1)$
-skeleton
$(n-1)$
-skeleton
![]() $K^{(n-1)}\subset K$
has
$K^{(n-1)}\subset K$
has
![]() $(-1)^{n-1}\chi (\widetilde K^{(n-1)}) = \mu ^{\prime \prime }_{n-1}(G)$
, by applying Wall’s construction of a normal form to replace K by a homotopy-equivalent complex if necessary (see [Reference Wall47, p. 238]).
$(-1)^{n-1}\chi (\widetilde K^{(n-1)}) = \mu ^{\prime \prime }_{n-1}(G)$
, by applying Wall’s construction of a normal form to replace K by a homotopy-equivalent complex if necessary (see [Reference Wall47, p. 238]).
The long exact sequences of the triples
![]() $(K, K^{(i)}, K^{(i-1)})$
, for cohomology with
$(K, K^{(i)}, K^{(i-1)})$
, for cohomology with
![]() $\mathbb Z G$
-coefficients gives:
$\mathbb Z G$
-coefficients gives:
If we let
![]() $Z^i := \ker \delta ^{i}$
and
$Z^i := \ker \delta ^{i}$
and
![]() $B^i := \operatorname {\mathrm {im}} \delta ^{i-1}$
(for later use) in the cochain complex
$B^i := \operatorname {\mathrm {im}} \delta ^{i-1}$
(for later use) in the cochain complex
![]() $(C^*, \delta ^*)$
, where
$(C^*, \delta ^*)$
, where
![]() $C^i = \operatorname {\mathrm {Hom}}_{\Lambda }(C_i, \Lambda )$
, then the sequence above becomes
$C^i = \operatorname {\mathrm {Hom}}_{\Lambda }(C_i, \Lambda )$
, then the sequence above becomes
Since
![]() $H^i(C) = H_{2n-i}(C) = 0$
, for
$H^i(C) = H_{2n-i}(C) = 0$
, for
![]() $n+1 \leq i \leq 2n-1$
, and
$n+1 \leq i \leq 2n-1$
, and
![]() $H^{2n}(C) = \mathbb Z$
, we can splice the short exact sequences
$H^{2n}(C) = \mathbb Z$
, we can splice the short exact sequences
for
![]() $n \leq i \leq 2n-1$
, and obtain a long exact sequence
$n \leq i \leq 2n-1$
, and obtain a long exact sequence
Since this a resolution of
![]() $\mathbb Z$
by finitely generated
$\mathbb Z$
by finitely generated
![]() $\mathbb Z G$
-modules, with
$\mathbb Z G$
-modules, with
![]() $\operatorname {\mathrm {rank}}_{\mathbb Z G} (C_i^*) := c_i$
, we have
$\operatorname {\mathrm {rank}}_{\mathbb Z G} (C_i^*) := c_i$
, we have
 $$ \begin{align*}(-1)^n\chi_{upper}(C) := (-1)^n\sum_{i=n}^{2n} (-1)^{i} c_i \geq \mu_{n}(G).\end{align*} $$
$$ \begin{align*}(-1)^n\chi_{upper}(C) := (-1)^n\sum_{i=n}^{2n} (-1)^{i} c_i \geq \mu_{n}(G).\end{align*} $$
On the other hand, by the normal form construction, we have
 $$ \begin{align*}(-1)^n\chi_{lower}(C) : = (-1)^n\sum_{i=0}^{n-1} (-1)^i c_i = (-1)^n(-1)^{n-1} \mu^{\prime\prime}_{n-1}(G) = -\mu^{\prime\prime}_{n-1}(G).\end{align*} $$
$$ \begin{align*}(-1)^n\chi_{lower}(C) : = (-1)^n\sum_{i=0}^{n-1} (-1)^i c_i = (-1)^n(-1)^{n-1} \mu^{\prime\prime}_{n-1}(G) = -\mu^{\prime\prime}_{n-1}(G).\end{align*} $$
Therefore,
![]() $q_{2n}(G) \geq (-1) ^n\chi (M) \geq \mu _{n}(G) -\mu ^{\prime \prime }_{n-1}(G)$
, as required.
$q_{2n}(G) \geq (-1) ^n\chi (M) \geq \mu _{n}(G) -\mu ^{\prime \prime }_{n-1}(G)$
, as required.
Remark 4.4. Note that
![]() $\mu ^{\prime }_1(G) \leq \mu _1(G) \leq d(G) -1$
by Swan [Reference Swan42, Proposition 1], so this is slightly different than the estimate in Theorem A for finite groups if
$\mu ^{\prime }_1(G) \leq \mu _1(G) \leq d(G) -1$
by Swan [Reference Swan42, Proposition 1], so this is slightly different than the estimate in Theorem A for finite groups if
![]() $n = 2$
.
$n = 2$
.
5 Rational homology 4–spheres
We now specialise our results to the case when M is a rational homology
![]() $4$
–sphere with finite fundamental group G. We would like to find restrictions on G by computing
$4$
–sphere with finite fundamental group G. We would like to find restrictions on G by computing
![]() $\mu _2(G)-\mu _1(G)$
. Note that
$\mu _2(G)-\mu _1(G)$
. Note that
![]() $\mu _1(G)=\mu _1'(G)$
and
$\mu _1(G)=\mu _1'(G)$
and
![]() $\mu _2(G)=\mu _2'(G)$
, and that for any solvable finite group,
$\mu _2(G)=\mu _2'(G)$
, and that for any solvable finite group,
![]() $\mu _1(G)= d(G)-1$
[Reference Cossey, Gruenberg and Kovács6, Proposition 1]. Let A denote a finite abelian group minimally generated by d elements, then using Theorem 2.7, we have the estimate
$\mu _1(G)= d(G)-1$
[Reference Cossey, Gruenberg and Kovács6, Proposition 1]. Let A denote a finite abelian group minimally generated by d elements, then using Theorem 2.7, we have the estimate
and so we recover the estimate proved in [Reference Teichner43, 3.4]:
Corollary 5.1. If G is a finite abelian group minimally generated by
![]() $k>3$
elements, then it cannot be realised as the fundamental group of a closed 4–manifold which is a rational homology sphere.
$k>3$
elements, then it cannot be realised as the fundamental group of a closed 4–manifold which is a rational homology sphere.
Our next objective will be to consider examples where twisted coefficients can be used to establish conditions for nonabelian groups. Recall the result due to Swan [Reference Swan42, Theorem 1.2 and Proposition 6.1]: for any finite group G,
![]() $\mu _n(G)$
is the smallest integer which is an upper bound on
$\mu _n(G)$
is the smallest integer which is an upper bound on
where K is a field, M is a
![]() $KG$
-module and
$KG$
-module and
![]() $h^n(G;M) := \dim _KH^n(G; M)$
. Moreover, we can assume that K is algebraically closed and has characteristic p dividing
$h^n(G;M) := \dim _KH^n(G; M)$
. Moreover, we can assume that K is algebraically closed and has characteristic p dividing
![]() $|G|$
, and it suffices to verify the upper bound on absolutely irreducible modules.
$|G|$
, and it suffices to verify the upper bound on absolutely irreducible modules.
We now focus on an interesting class of nonabelian groups for which the absolutely irreducible modules are easy to determine. The following proposition follows from elementary representation theory (see [Reference Webb52, Corollary 6.2.2]).
Proposition 5.2. Let K be a field of characteristic p, G a finite group with maximal normal p–group denoted by
![]() $O_p(G)$
. Then the simple
$O_p(G)$
. Then the simple
![]() $KG$
–modules are precisely the simple
$KG$
–modules are precisely the simple
![]() $K[G/O_p(G)]$
–modules, made into
$K[G/O_p(G)]$
–modules, made into
![]() $KG$
–modules via the quotient homomorphism
$KG$
–modules via the quotient homomorphism
![]() $G\to G/O_p(G)$
.
$G\to G/O_p(G)$
.
Corollary 5.3. Let
![]() $U_k=E_k\times _TC$
denote a semidirect product, where
$U_k=E_k\times _TC$
denote a semidirect product, where
![]() $E_k\cong (\mathbb Z/p\mathbb Z)^k$
with
$E_k\cong (\mathbb Z/p\mathbb Z)^k$
with
![]() $k>1$
and C is cyclic of order relatively prime to p. Then for any algebraically closed field
$k>1$
and C is cyclic of order relatively prime to p. Then for any algebraically closed field
![]() $\mathbb K_p$
of characteristic p, the absolutely irreducible
$\mathbb K_p$
of characteristic p, the absolutely irreducible
![]() $\mathbb K_pU_k$
–modules are one-dimensional characters
$\mathbb K_pU_k$
–modules are one-dimensional characters
![]() $\alpha \colon C \to \mathbb K_p^{\times }$
on which
$\alpha \colon C \to \mathbb K_p^{\times }$
on which
![]() $E_k$
acts trivially.
$E_k$
acts trivially.
The cyclic group C acts on the vector spaces
![]() $H^i(E_k; \mathbb K_p)$
via one-dimensional characters
$H^i(E_k; \mathbb K_p)$
via one-dimensional characters
![]() $\alpha \colon C \to \mathbb K_p^{\times }$
. Using the multiplicative structure in cohomology and the Bockstein, this is determined by
$\alpha \colon C \to \mathbb K_p^{\times }$
. Using the multiplicative structure in cohomology and the Bockstein, this is determined by
![]() $N_k=H^1(E_k;\mathbb K_p)\cong \operatorname {\mathrm {Hom}} (E_k, \mathbb K_p)$
as an
$N_k=H^1(E_k;\mathbb K_p)\cong \operatorname {\mathrm {Hom}} (E_k, \mathbb K_p)$
as an
![]() $\mathbb K_p[C]$
–module.
$\mathbb K_p[C]$
–module.
Recall that by [Reference Adem and Milgram2, Corollary II.4.3, Theorem II.4.4], the mod p cohomology ring of
![]() $E_k$
is given by
$E_k$
is given by
 $$ \begin{align*}H^*(E_k, \mathbb F_p)\cong \begin{cases} \mathbb F_2 [x_1, \dots , x_k] & \text{for } p=2\\ \Lambda (x_1, \dots, x_k)\otimes \mathbb F_p [y_1, \dots, y_k] & \text{for } p \text{ odd} \end{cases}, \end{align*} $$
$$ \begin{align*}H^*(E_k, \mathbb F_p)\cong \begin{cases} \mathbb F_2 [x_1, \dots , x_k] & \text{for } p=2\\ \Lambda (x_1, \dots, x_k)\otimes \mathbb F_p [y_1, \dots, y_k] & \text{for } p \text{ odd} \end{cases}, \end{align*} $$
where
![]() $x_1, \dots , x_k\in H^1(E_k, \mathbb F_p)$
,
$x_1, \dots , x_k\in H^1(E_k, \mathbb F_p)$
,
![]() $y_1,\dots ,y_k\in H^2(E_k, \mathbb F_p)$
and
$y_1,\dots ,y_k\in H^2(E_k, \mathbb F_p)$
and
![]() $\Lambda (x_1, \dots , x_k)$
denotes the exterior algebra on these one-dimensional generators. Moreover, if we let
$\Lambda (x_1, \dots , x_k)$
denotes the exterior algebra on these one-dimensional generators. Moreover, if we let
![]() $B\colon H^1(E_k, \mathbb F_p)\to H^2(E_k, \mathbb F_p)$
denote the Bockstein, then we can assume that for p odd
$B\colon H^1(E_k, \mathbb F_p)\to H^2(E_k, \mathbb F_p)$
denote the Bockstein, then we can assume that for p odd
![]() $B(x_i)= y_i$
, whereas for
$B(x_i)= y_i$
, whereas for
![]() $p=2$
,
$p=2$
,
![]() $B(x_i)=x_i^2$
for all
$B(x_i)=x_i^2$
for all
![]() $i=1, \dots , k$
. By extending coefficients, we obtain the same structure for
$i=1, \dots , k$
. By extending coefficients, we obtain the same structure for
![]() $H^*(E_k, \mathbb K_p)$
.
$H^*(E_k, \mathbb K_p)$
.
The map B is compatible with respect to the C action and defines an isomorphism onto its image, thus giving rise to an exact sequence
as
![]() $\mathbb K_pC$
–modules. If
$\mathbb K_pC$
–modules. If
![]() $N_k\cong \bigoplus _{1\le i\le k} L(\alpha _i)$
then
$N_k\cong \bigoplus _{1\le i\le k} L(\alpha _i)$
then
![]() $\Lambda ^2(N_k)\cong \bigoplus _{1\le i<j\le k} L(\alpha _i\alpha _j)$
. Note that if we tensor the sequence with any other character and take C–invariants, it will still be exact, as
$\Lambda ^2(N_k)\cong \bigoplus _{1\le i<j\le k} L(\alpha _i\alpha _j)$
. Note that if we tensor the sequence with any other character and take C–invariants, it will still be exact, as
![]() $(|C|,p)=1$
.
$(|C|,p)=1$
.
Using the fact that for any
![]() $\mathbb K_pU_k$
–module M,
$\mathbb K_pU_k$
–module M,
![]() $H^t(U_k; M) \cong H^t(E_k; M_{|_E})^C$
for every
$H^t(U_k; M) \cong H^t(E_k; M_{|_E})^C$
for every
![]() $t\ge 0$
, for any character
$t\ge 0$
, for any character
![]() $L(\beta )$
, we obtain the formula
$L(\beta )$
, we obtain the formula
At primes q dividing
![]() $ |C|$
, we work over the field
$ |C|$
, we work over the field
![]() $\mathbb K_q$
, and note that
$\mathbb K_q$
, and note that
![]() $H^i(U_k, L)= H^i(C, L^{E_k})$
. Hence, an absolutely irreducible L with some
$H^i(U_k, L)= H^i(C, L^{E_k})$
. Hence, an absolutely irreducible L with some
![]() $h^i(U_k,L)\ne 0$
must also have a trivial action of
$h^i(U_k,L)\ne 0$
must also have a trivial action of
![]() $E_k$
. Arguing, as before, L is the inflation of a character
$E_k$
. Arguing, as before, L is the inflation of a character
![]() $C/O_q(C)\to \mathbb K_q^{\times }$
. Thus, we have
$C/O_q(C)\to \mathbb K_q^{\times }$
. Thus, we have
![]() $H^i(U_k, L)= [H^i(O_q(C), \mathbb K_q)\otimes L]^{C/O_q(C)}$
. As
$H^i(U_k, L)= [H^i(O_q(C), \mathbb K_q)\otimes L]^{C/O_q(C)}$
. As
![]() $O_q(C)$
is cyclic, all these terms are isomorphic and of nonzero rank (equal to one) if and only if the action of
$O_q(C)$
is cyclic, all these terms are isomorphic and of nonzero rank (equal to one) if and only if the action of
![]() $C/O_q(C)$
is trivial, and we obtain that
$C/O_q(C)$
is trivial, and we obtain that
We apply our analysis to obtain a calculation for
![]() $\mu _2(U_k)$
and
$\mu _2(U_k)$
and
![]() $e_2(U_k)$
:
$e_2(U_k)$
:
Proposition 5.4. For
![]() $U_k = E_k\times _T C$
as above, with
$U_k = E_k\times _T C$
as above, with
![]() $N_k=H^1(E_k; \mathbb K_p)$
,
$N_k=H^1(E_k; \mathbb K_p)$
,
as
![]() $L(\beta )$
ranges over all characters
$L(\beta )$
ranges over all characters
![]() $\beta \colon C \to \mathbb K_p^{\times }$
, and
$\beta \colon C \to \mathbb K_p^{\times }$
, and
We apply this to the special case when p is an odd prime and the action on
![]() $N_k=H^1(E_k, \mathbb K_p)$
is isotypic, that is it is the direct sum of copies of a fixed character
$N_k=H^1(E_k, \mathbb K_p)$
is isotypic, that is it is the direct sum of copies of a fixed character
![]() $L(\alpha )$
.
$L(\alpha )$
.
Corollary 5.5. Let
![]() $U_k = E_k\times _T C$
, where p is odd and the action of C on the vector space
$U_k = E_k\times _T C$
, where p is odd and the action of C on the vector space
![]() $E_k$
gives rise to the sum of k copies of a fixed character
$E_k$
gives rise to the sum of k copies of a fixed character
![]() $L(\alpha )$
over the splitting field
$L(\alpha )$
over the splitting field
![]() $\mathbb K_p$
, with
$\mathbb K_p$
, with
![]() $k>1$
.
$k>1$
.
-
(i) If
 $\alpha ^2\ne 1$
,
$\alpha ^2\ne 1$
,
 $e_2(U_k)=2$
,
$e_2(U_k)=2$
,
 $\mu _2(U_k) = \frac {k(k-1)}{2}$
and
$\mu _2(U_k) = \frac {k(k-1)}{2}$
and
 $\mu _2(U_k)-\mu _1(U_k) = \frac {k(k-3)}{2}.$
$\mu _2(U_k)-\mu _1(U_k) = \frac {k(k-3)}{2}.$
-
(ii) If
 $\alpha ^2=1$
,
$\alpha ^2=1$
,
 $e_2(U_k) = \frac {k(k-1)}{2} + 2$
,
$e_2(U_k) = \frac {k(k-1)}{2} + 2$
,
 $\mu _2(U_k) = \frac {k(k-1)}{2} + 1$
and
$\mu _2(U_k) = \frac {k(k-1)}{2} + 1$
and
 $\mu _2(U_k) - \mu _1(U_k) = \frac {k(k-3)}{2} + 1.$
$\mu _2(U_k) - \mu _1(U_k) = \frac {k(k-3)}{2} + 1.$
Proof. We apply Proposition 5.4 to compute
![]() $\mu _2(U_k)$
and
$\mu _2(U_k)$
and
![]() $e_2(U_k)$
. Choose
$e_2(U_k)$
. Choose
![]() $\beta = \alpha ^{-2}$
, then
$\beta = \alpha ^{-2}$
, then
![]() $\Lambda ^2(H^1(E_k;\mathbb K_p))\otimes L(\beta )$
is a trivial
$\Lambda ^2(H^1(E_k;\mathbb K_p))\otimes L(\beta )$
is a trivial
![]() $\mathbb K_p[C]$
–module of dimension equal to
$\mathbb K_p[C]$
–module of dimension equal to
![]() $\frac {k(k-1)}{2}$
. In the special case
$\frac {k(k-1)}{2}$
. In the special case
![]() $\beta =1$
, we obtain the extra term. The calculation for
$\beta =1$
, we obtain the extra term. The calculation for
![]() $e_2(U_k)$
follows from its expression in terms of invariants. As
$e_2(U_k)$
follows from its expression in terms of invariants. As
![]() $U_k$
is solvable, we have
$U_k$
is solvable, we have
![]() $\mu _1(U_k) =k$
, and the proof is complete.
$\mu _1(U_k) =k$
, and the proof is complete.
Corollary 5.6. Let
![]() $U_k=E_k\times _T C$
, where p is odd,
$U_k=E_k\times _T C$
, where p is odd,
![]() $E_k=(\mathbb Z/p\mathbb Z)^k$
and C cyclic of order prime to p acts on each
$E_k=(\mathbb Z/p\mathbb Z)^k$
and C cyclic of order prime to p acts on each
![]() $\mathbb Z/p\mathbb Z$
factor in
$\mathbb Z/p\mathbb Z$
factor in
![]() $E_k$
via
$E_k$
via
![]() $x\mapsto x^q$
, where q is a unit in
$x\mapsto x^q$
, where q is a unit in
![]() $\mathbb Z/p\mathbb Z$
.
$\mathbb Z/p\mathbb Z$
.
-
(i) If
 $x^{q^2}\ne x$
for all
$x^{q^2}\ne x$
for all
 $1\ne x\in E_k$
, then
$1\ne x\in E_k$
, then  $$ \begin{align*}\max\{2, \frac{k(k-3)}{2}\} \le q_4(U_k) \le k(k-1).\end{align*} $$
$$ \begin{align*}\max\{2, \frac{k(k-3)}{2}\} \le q_4(U_k) \le k(k-1).\end{align*} $$
-
(ii) If
 $q=p-1$
, then
$q=p-1$
, then  $$ \begin{align*}\frac{k(k-1)}{2} + 2 \le q_4(U_k)\le k(k-1) + 2.\end{align*} $$
$$ \begin{align*}\frac{k(k-1)}{2} + 2 \le q_4(U_k)\le k(k-1) + 2.\end{align*} $$
Remark 5.7. Note that for
![]() $\alpha ^2\ne 1$
,
$\alpha ^2\ne 1$
,
![]() $e_2(U_k)=2 < \mu _2(U_k)-\mu _1(U_k)$
for
$e_2(U_k)=2 < \mu _2(U_k)-\mu _1(U_k)$
for
![]() $k\ge 5$
. Hence, 5.6 improves on the lower bound given in [Reference Hausmann and Weinberger19]. On the other hand, if
$k\ge 5$
. Hence, 5.6 improves on the lower bound given in [Reference Hausmann and Weinberger19]. On the other hand, if
![]() $\alpha ^2 =1$
, then
$\alpha ^2 =1$
, then
![]() $\mu _2(U_k) - \mu _1(U_k) < e_2(U_k)$
for all
$\mu _2(U_k) - \mu _1(U_k) < e_2(U_k)$
for all
![]() $k>1$
. This shows that the two invariants play a role in establishing lower bounds for
$k>1$
. This shows that the two invariants play a role in establishing lower bounds for
![]() $q_4(G)$
.
$q_4(G)$
.
We now apply our estimate to homology 4–spheres.
Theorem 5.8. Let
![]() $U_k=E_k\times _T C$
, where p is an odd prime,
$U_k=E_k\times _T C$
, where p is an odd prime,
![]() $E_k=(\mathbb Z/p\mathbb Z)^k$
and C cyclic of order prime to p acts on each
$E_k=(\mathbb Z/p\mathbb Z)^k$
and C cyclic of order prime to p acts on each
![]() $\mathbb Z/p\mathbb Z$
factor in
$\mathbb Z/p\mathbb Z$
factor in
![]() $E_k$
via
$E_k$
via
![]() $x\mapsto x^q$
, where q is a unit in
$x\mapsto x^q$
, where q is a unit in
![]() $\mathbb Z/p\mathbb Z$
.
$\mathbb Z/p\mathbb Z$
.
-
(i) If
 $x^{q^2}\ne x$
for all
$x^{q^2}\ne x$
for all
 $1\ne x\in E_k$
, then for all
$1\ne x\in E_k$
, then for all
 $k>4$
,
$k>4$
,
 $U_k$
does not arise as the fundamental group of any rational homology 4–sphere.
$U_k$
does not arise as the fundamental group of any rational homology 4–sphere. -
(ii) If
 $q=p-1$
, then for all
$q=p-1$
, then for all
 $k>1$
,
$k>1$
,
 $U_k$
does not arise as the fundamental group of any rational homology 4–sphere.
$U_k$
does not arise as the fundamental group of any rational homology 4–sphere.
Proof. For the groups
![]() $U_k= E_k\times _TC$
, where
$U_k= E_k\times _TC$
, where
![]() $x^{q^2}\ne x$
for
$x^{q^2}\ne x$
for
![]() $x\in E_k$
, we consider the inequality
$x\in E_k$
, we consider the inequality
If a rational homology 4–sphere X with fundamental group
![]() $U_k$
exists, then
$U_k$
exists, then
![]() $q_4(U_k)=2$
and we’d have
$q_4(U_k)=2$
and we’d have
![]() $\frac {k(k-3)}{2} \le 2$
, which implies that
$\frac {k(k-3)}{2} \le 2$
, which implies that
![]() $k\le 4$
. Note that the upper bound implies the existence of a rational homology 4–sphere with fundamental group
$k\le 4$
. Note that the upper bound implies the existence of a rational homology 4–sphere with fundamental group
![]() $U_2$
. In the case when
$U_2$
. In the case when
![]() $q=p-1$
, our estimate 5.6 shows that
$q=p-1$
, our estimate 5.6 shows that
![]() $2< q_4(U_k)$
for all
$2< q_4(U_k)$
for all
![]() $k>1$
.
$k>1$
.
Example 5.9. Let
![]() $\mathbb F_q$
denote a field with
$\mathbb F_q$
denote a field with
![]() $q=2^k$
elements. Then the cyclic group of units
$q=2^k$
elements. Then the cyclic group of units
![]() $C=\mathbb Z/(q-1)\mathbb Z$
acts transitively on the nonzero elements of the underlying mod 2 vector space
$C=\mathbb Z/(q-1)\mathbb Z$
acts transitively on the nonzero elements of the underlying mod 2 vector space
![]() $E_k=(\mathbb Z/2\mathbb Z)^k$
. If we write
$E_k=(\mathbb Z/2\mathbb Z)^k$
. If we write
![]() $\mathbb F_q = \mathbb F_2[u]/(p(u))$
, where
$\mathbb F_q = \mathbb F_2[u]/(p(u))$
, where
![]() $p(u)$
is an irreducible polynomial of degree k over
$p(u)$
is an irreducible polynomial of degree k over
![]() $\mathbb F_2$
, then the action can be described as multiplication by u. Expressing it in terms of the basis
$\mathbb F_2$
, then the action can be described as multiplication by u. Expressing it in terms of the basis
![]() $\{1,u,\dots ,u^{k-1}\}$
, we obtain a faithful representation
$\{1,u,\dots ,u^{k-1}\}$
, we obtain a faithful representation
![]() $C\to GL(k,\mathbb F_2)$
with characteristic polynomial
$C\to GL(k,\mathbb F_2)$
with characteristic polynomial
![]() $p(t)$
. This gives rise to a semidirect product
$p(t)$
. This gives rise to a semidirect product
![]() $J_k= E_k\times _TC$
, where the action of C on
$J_k= E_k\times _TC$
, where the action of C on
![]() $N_k=H^1(E_k,\mathbb K_2)$
decomposes into nontrivial, distinct characters determined by the roots of
$N_k=H^1(E_k,\mathbb K_2)$
decomposes into nontrivial, distinct characters determined by the roots of
![]() $p(t)$
. If
$p(t)$
. If
![]() $\alpha $
is a root of this polynomial, so are all the powers
$\alpha $
is a root of this polynomial, so are all the powers
![]() $\{\alpha ^{2^i}\}_{i=0,\dots ,k-1}$
, and these appear as a complete set of eigenvalues for the action on the k–dimensional vector space. In other words, we have
$\{\alpha ^{2^i}\}_{i=0,\dots ,k-1}$
, and these appear as a complete set of eigenvalues for the action on the k–dimensional vector space. In other words, we have
![]() $N_k\cong \bigoplus _{0\le i\le k-1} L(\alpha ^{2^i})$
. We propose to compute the invariants
$N_k\cong \bigoplus _{0\le i\le k-1} L(\alpha ^{2^i})$
. We propose to compute the invariants
![]() $\mu _2(J_k)$
and
$\mu _2(J_k)$
and
![]() $e_2(J_k)$
.
$e_2(J_k)$
.
Proposition 5.10. For the groups
![]() $J_k$
described above, we have
$J_k$
described above, we have
-
(i)
 $\mu _2(J_2) = 2$
, whereas
$\mu _2(J_2) = 2$
, whereas
 $\mu _2(J_k)=1$
for all
$\mu _2(J_k)=1$
for all
 $k>2$
.
$k>2$
. -
(ii)
 $e_2(J_2)=3$
, whereas
$e_2(J_2)=3$
, whereas
 $e_2(J_k)=2$
for all
$e_2(J_k)=2$
for all
 $k>2$
.
$k>2$
.
Proof. As
![]() $N_k\cong \bigoplus _{0\le i\le k-1} L(\alpha ^{2^i})$
, we have that
$N_k\cong \bigoplus _{0\le i\le k-1} L(\alpha ^{2^i})$
, we have that
![]() $\Lambda ^2(N_k)\cong \bigoplus _{0\le i<j\le k-1} L(\alpha ^{2^i+2^j})$
. For
$\Lambda ^2(N_k)\cong \bigoplus _{0\le i<j\le k-1} L(\alpha ^{2^i+2^j})$
. For
![]() $k>2$
, this is a sum of distinct, nontrivial characters. This follows from the fact that for
$k>2$
, this is a sum of distinct, nontrivial characters. This follows from the fact that for
![]() $k>2$
,
$k>2$
,
and each
![]() $\alpha ^{2^i+2^j}$
is a distinct, nontrivial
$\alpha ^{2^i+2^j}$
is a distinct, nontrivial
![]() $2^k-1$
root of unity. Hence, if
$2^k-1$
root of unity. Hence, if
![]() $k>2$
, the module
$k>2$
, the module
![]() $\Lambda ^2(N_k)$
has no trivial summands and no repeated summands. Now, if we take any character
$\Lambda ^2(N_k)$
has no trivial summands and no repeated summands. Now, if we take any character
![]() $L(\beta )$
, we see that at most one summand in
$L(\beta )$
, we see that at most one summand in
![]() $\Lambda ^2(N_k)\otimes L(\beta )$
can be trivial. And if this occurs, then
$\Lambda ^2(N_k)\otimes L(\beta )$
can be trivial. And if this occurs, then
![]() $\beta \ne 1$
. Hence, applying the formula in Proposition 5.4, we conclude that
$\beta \ne 1$
. Hence, applying the formula in Proposition 5.4, we conclude that
![]() $\mu _2(J_k)=1$
. Similarly, we see that
$\mu _2(J_k)=1$
. Similarly, we see that
![]() $e_2(J_k)=2$
for all
$e_2(J_k)=2$
for all
![]() $k>2$
. Also
$k>2$
. Also
![]() $\Lambda ^2(N_2)\cong L(1)$
, whence we see that
$\Lambda ^2(N_2)\cong L(1)$
, whence we see that
![]() $\mu _2(J_2)=2$
and
$\mu _2(J_2)=2$
and
![]() $e_2(J_2)=3$
.
$e_2(J_2)=3$
.
From these examples, we conclude that there exist rational homology 4–spheres with fundamental group equal to
![]() $J_k$
for
$J_k$
for
![]() $k>2$
, and so groups of arbitrarily high rank can occur as such groups, in contrast to the situation for abelian groups appearing in Corollary 5.1. For
$k>2$
, and so groups of arbitrarily high rank can occur as such groups, in contrast to the situation for abelian groups appearing in Corollary 5.1. For
![]() $J_2\cong A_4$
, the alternating group on four letters, we have
$J_2\cong A_4$
, the alternating group on four letters, we have
![]() $e_2(J_2)=3$
,
$e_2(J_2)=3$
,
![]() $\mu _2(J_2)=2$
, and so
$\mu _2(J_2)=2$
, and so
![]() $3\le q_4( A_4)\le 4$
. The cohomological computations also imply that
$3\le q_4( A_4)\le 4$
. The cohomological computations also imply that
![]() $\mu _4( A_4)=1$
, whence, there does exist a rational homology
$\mu _4( A_4)=1$
, whence, there does exist a rational homology
![]() $8$
–sphere with fundamental group
$8$
–sphere with fundamental group
![]() $ A_4$
.
$ A_4$
.
Proposition 5.11. For the alternating groups
![]() $G = A_4$
or
$G = A_4$
or
![]() $G=A_5$
, we have
$G=A_5$
, we have
![]() $q_4(G) = 4$
.
$q_4(G) = 4$
.
Proof. By the estimates above, for
![]() $G= A_4$
, we only need to rule out
$G= A_4$
, we only need to rule out
![]() $q_4(G) = 3$
, so suppose that there exists
$q_4(G) = 3$
, so suppose that there exists
![]() $M^4$
with
$M^4$
with
![]() $\pi _1(M) = A_4$
and
$\pi _1(M) = A_4$
and
![]() $\chi (M) = 3$
. Applying the universal coefficient theorem, we can use the computation at
$\chi (M) = 3$
. Applying the universal coefficient theorem, we can use the computation at
![]() $p=2$
(see [Reference Adem and Milgram2, Theorem 1.3, Chapter III]) to show that
$p=2$
(see [Reference Adem and Milgram2, Theorem 1.3, Chapter III]) to show that
![]() $H_4(A_4;\mathbb Z) = 0$
. Hence,
$H_4(A_4;\mathbb Z) = 0$
. Hence,
![]() $\widehat H^{-5}(A_4,\mathbb Z)=0$
and applying Proposition 2.5, we infer that
$\widehat H^{-5}(A_4,\mathbb Z)=0$
and applying Proposition 2.5, we infer that
![]() $ \pi _2(M)$
is stably isomorphic to
$ \pi _2(M)$
is stably isomorphic to
![]() $J \oplus J^*$
, where J denotes a minimal representative of
$J \oplus J^*$
, where J denotes a minimal representative of
![]() $\Omega ^3(\mathbb Z)$
. Since
$\Omega ^3(\mathbb Z)$
. Since
![]() $\chi (M) = 3$
, we have
$\chi (M) = 3$
, we have
![]() $H^0(G; \pi _2(M)) = \mathbb Z$
. From the exact sequence for Tate cohomology [Reference Brown3, Chapter IV.4], we have a surjection
$H^0(G; \pi _2(M)) = \mathbb Z$
. From the exact sequence for Tate cohomology [Reference Brown3, Chapter IV.4], we have a surjection
![]() $\mathbb Z = H^0(G;\pi _2(M)) \twoheadrightarrow \widehat H^0(G;\pi _2(M))$
. However,
$\mathbb Z = H^0(G;\pi _2(M)) \twoheadrightarrow \widehat H^0(G;\pi _2(M))$
. However,
and since
![]() $H_2(G;\mathbb Z) = \mathbb Z/{2}\mathbb Z$
, this is impossible. For
$H_2(G;\mathbb Z) = \mathbb Z/{2}\mathbb Z$
, this is impossible. For
![]() $G= A_5$
, we apply the fact that for every nonperiodic finite subgroup G of
$G= A_5$
, we apply the fact that for every nonperiodic finite subgroup G of
![]() $SO(3)$
,
$SO(3)$
,
![]() $\mu _2(G)=2$
(see Remark 6.3). The rest of the argument is analogous to that for
$\mu _2(G)=2$
(see Remark 6.3). The rest of the argument is analogous to that for
![]() $A_4$
, since the restriction map
$A_4$
, since the restriction map
![]() $H^*(A_5;\mathbb Z/2\mathbb Z) \to H^*(A_4; \mathbb Z/2\mathbb Z)$
is an isomorphism. This is true because both groups share the same
$H^*(A_5;\mathbb Z/2\mathbb Z) \to H^*(A_4; \mathbb Z/2\mathbb Z)$
is an isomorphism. This is true because both groups share the same
![]() $2$
–Sylow subgroup
$2$
–Sylow subgroup
![]() $(\mathbb Z/2\mathbb Z)^2$
, with normaliser
$(\mathbb Z/2\mathbb Z)^2$
, with normaliser
![]() $A_4$
(see [Reference Adem and Milgram2, Theorem 6.8, Chapter II]). This implies that
$A_4$
(see [Reference Adem and Milgram2, Theorem 6.8, Chapter II]). This implies that
![]() $e_2(A_5)=3$
,
$e_2(A_5)=3$
,
![]() $H_4(A_5;\mathbb Z) = 0$
and
$H_4(A_5;\mathbb Z) = 0$
and
![]() $H_2(A_5;\mathbb Z) = \mathbb Z/{2}\mathbb Z$
(note that the other two p–Sylow subgroups are cyclic, so don’t contribute to even degree homology). Therefore, we can rule out
$H_2(A_5;\mathbb Z) = \mathbb Z/{2}\mathbb Z$
(note that the other two p–Sylow subgroups are cyclic, so don’t contribute to even degree homology). Therefore, we can rule out
![]() $q_4(A_5)=3$
whence
$q_4(A_5)=3$
whence
![]() $q_4(A_5)=4$
.
$q_4(A_5)=4$
.
6 Some further remarks and questions in dimension four
In this section, we will briefly discuss some questions about rational homology
![]() $4$
-spheres whose fundamental groups are finite.
$4$
-spheres whose fundamental groups are finite.
Section 6A. Existence via surgery. The main open problem is to characterise the finite groups G for which
![]() $q_4(G)=2$
. To make progress, we need more constructions of rational homology
$q_4(G)=2$
. To make progress, we need more constructions of rational homology
![]() $4$
-spheres.
$4$
-spheres.
Examples of
![]() $\mathbb Q S^4$
-manifolds can be constructed by starting with a rational homology
$\mathbb Q S^4$
-manifolds can be constructed by starting with a rational homology
![]() $3$
-sphere X, forming the product
$3$
-sphere X, forming the product
![]() $X \times S^1$
, and then doing surgery on an embedded
$X \times S^1$
, and then doing surgery on an embedded
![]() $S^1 \times D^3 \subset X \times S^1$
representing a generator of
$S^1 \times D^3 \subset X \times S^1$
representing a generator of
![]() $\pi _1(S^1) = \mathbb Z$
. This construction is equivalent to the ‘thickened double’ construction
$\pi _1(S^1) = \mathbb Z$
. This construction is equivalent to the ‘thickened double’ construction
![]() $Z = M(K)$
for a finite
$Z = M(K)$
for a finite
![]() $2$
-complex of Proposition 3.1 (compare [Reference Hambleton and Kreck13, Section 4]).
$2$
-complex of Proposition 3.1 (compare [Reference Hambleton and Kreck13, Section 4]).
Example 6.1. The groups
![]() $G=\mathbb Z/{p}\mathbb Z \times \mathbb Z/{p}\mathbb Z$
are
$G=\mathbb Z/{p}\mathbb Z \times \mathbb Z/{p}\mathbb Z$
are
![]() $\mathbb Q S^4$
-groups, since we can do surgery on an embedded circle
$\mathbb Q S^4$
-groups, since we can do surgery on an embedded circle
![]() $L^3(p,1) \times S^1$
representing p-times a generator of
$L^3(p,1) \times S^1$
representing p-times a generator of
![]() $\pi _1(S^1) = \mathbb Z$
. These examples are not of the thickened double form
$\pi _1(S^1) = \mathbb Z$
. These examples are not of the thickened double form
![]() $M(K)$
because the minimal rank of
$M(K)$
because the minimal rank of
![]() $\pi _2(K)$
representing
$\pi _2(K)$
representing
![]() $\Omega ^3(\mathbb Z)$
is greater than
$\Omega ^3(\mathbb Z)$
is greater than
![]() $|G|-1$
, and hence, the extension describing
$|G|-1$
, and hence, the extension describing
![]() $\pi _2(M)$
is nontrivial (by Proposition 2.3).
$\pi _2(M)$
is nontrivial (by Proposition 2.3).
Since the quotient of a free finite group action on a rational homology
![]() $3$
-sphere is again a rational homology
$3$
-sphere is again a rational homology
![]() $3$
-sphere, one could use the examples
$3$
-sphere, one could use the examples
![]() $X=Y/G$
studied by [Reference Adem and Hambleton1], where Y is a
$X=Y/G$
studied by [Reference Adem and Hambleton1], where Y is a
![]() $\mathbb Q S^3$
and G is a finite group acting freely on Y. However, to obtain a
$\mathbb Q S^3$
and G is a finite group acting freely on Y. However, to obtain a
![]() $\mathbb Q S^4$
with finite fundamental group by this construction, Y must, itself, have finite fundamental group.
$\mathbb Q S^4$
with finite fundamental group by this construction, Y must, itself, have finite fundamental group.
Remark 6.2. The finite fundamental groups of closed, oriented
![]() $3$
-manifolds have periodic cohomology of period 4, but not all
$3$
-manifolds have periodic cohomology of period 4, but not all
![]() $4$
-periodic groups arise this way. A complete list of
$4$
-periodic groups arise this way. A complete list of
![]() $4$
-periodic groups is given in Milnor [Reference Milnor32, Section 3], and those which can act freely and orthogonally on
$4$
-periodic groups is given in Milnor [Reference Milnor32, Section 3], and those which can act freely and orthogonally on
![]() $S^3$
were listed by Hopf [Reference Hopf20]. Perelman [Reference Lott26] showed that the remaining groups in Milnor’s list do not arise as the fundamental group of any closed, oriented
$S^3$
were listed by Hopf [Reference Hopf20]. Perelman [Reference Lott26] showed that the remaining groups in Milnor’s list do not arise as the fundamental group of any closed, oriented
![]() $3$
-manifold, and that the closed
$3$
-manifold, and that the closed
![]() $3$
-manifolds with finite fundamental group are exactly the
$3$
-manifolds with finite fundamental group are exactly the
![]() $3$
-dimensional spherical space forms.
$3$
-dimensional spherical space forms.
Remark 6.3. For every nonperiodic finite subgroup G of
![]() $SO(3)$
, we have
$SO(3)$
, we have
![]() $\mu _2(G)=2$
, and hence,
$\mu _2(G)=2$
, and hence,
![]() $q_4(G) \leq 4$
(see [Reference Hambleton and Kreck15, Proposition 2.4]). Note that each such subgroup has a
$q_4(G) \leq 4$
(see [Reference Hambleton and Kreck15, Proposition 2.4]). Note that each such subgroup has a
![]() $2$
-fold central extension
$2$
-fold central extension
![]() $G^* \subset SU(2)$
which acts freely on
$G^* \subset SU(2)$
which acts freely on
![]() $S^3$
, and let
$S^3$
, and let
![]() $X =S^3/G^*$
denote the quotient
$X =S^3/G^*$
denote the quotient
![]() $3$
-manifold. On
$3$
-manifold. On
![]() $N:=X \times S^1$
, we can do surgery on disjoint circles representing (i) a generator of the central subgroup of
$N:=X \times S^1$
, we can do surgery on disjoint circles representing (i) a generator of the central subgroup of
![]() $G^*$
and (ii) a generator of
$G^*$
and (ii) a generator of
![]() $\mathbb Z$
, to reduce the fundamental group from
$\mathbb Z$
, to reduce the fundamental group from
![]() $\pi _1(N) = G^* \times \mathbb Z$
to G. We thus obtain a
$\pi _1(N) = G^* \times \mathbb Z$
to G. We thus obtain a
![]() $4$
-manifold M with
$4$
-manifold M with
![]() $\chi (M)=4$
and
$\chi (M)=4$
and
![]() $\pi _1(M) = G$
, realising the upper bound for
$\pi _1(M) = G$
, realising the upper bound for
![]() $q_4(G)$
. Our estimates give
$q_4(G)$
. Our estimates give
![]() $2 \leq q_4(G) \leq 4$
for the cases not yet determined, namely, where G is dihedral of order
$2 \leq q_4(G) \leq 4$
for the cases not yet determined, namely, where G is dihedral of order
![]() $4n$
or G is the symmetric group
$4n$
or G is the symmetric group
![]() $S_4$
.
$S_4$
.
Remark 6.4. Teichner [Reference Teichner43, 3.7] indicated that topological surgery could produce examples with finite fundamental group from certain
![]() $4$
-manifolds with infinite fundamental group. This technique should be investigated further.
$4$
-manifolds with infinite fundamental group. This technique should be investigated further.
Section 6B. Groups of deficiency zero. There are many finite groups with deficiency zero: for example, Wamsley [Reference Wamsley51] showed that a metacyclic group G with
![]() $H_2(G;\mathbb Z) =0$
has
$H_2(G;\mathbb Z) =0$
has
![]() $\operatorname {\mathrm {Def}}(G) = 0$
. In particular, the class of finite groups arising as fundamental groups of rational homology 4–spheres includes groups with periodic cohomology of arbitrarily high period. There is an extensive literature on this problem: for example, see [Reference Campbell and Robertson4, Reference Campbell and Robertson5, Reference Cossey, Gruenberg and Kovács6, Reference Epstein8, Reference Johnson and Wamsley22, Reference Mennicke and Neumann30, Reference Neumann33, Reference Sag and Wamsley37, Reference Sag and Wamsley38, Reference Searby and Wamsley39].
$\operatorname {\mathrm {Def}}(G) = 0$
. In particular, the class of finite groups arising as fundamental groups of rational homology 4–spheres includes groups with periodic cohomology of arbitrarily high period. There is an extensive literature on this problem: for example, see [Reference Campbell and Robertson4, Reference Campbell and Robertson5, Reference Cossey, Gruenberg and Kovács6, Reference Epstein8, Reference Johnson and Wamsley22, Reference Mennicke and Neumann30, Reference Neumann33, Reference Sag and Wamsley37, Reference Sag and Wamsley38, Reference Searby and Wamsley39].
According to Swan,
![]() $1\leq \mu _2(G) \leq 1 - \operatorname {\mathrm {Def}}(G)$
(see [Reference Swan42, Proposition 1, Corollary 1.3]), hence, if G is a finite group of deficiency zero, we have
$1\leq \mu _2(G) \leq 1 - \operatorname {\mathrm {Def}}(G)$
(see [Reference Swan42, Proposition 1, Corollary 1.3]), hence, if G is a finite group of deficiency zero, we have
![]() $\mu _2(G)=1$
. Thus, for such groups by Proposition 3.1, we can construct an orientable 4–manifold M with
$\mu _2(G)=1$
. Thus, for such groups by Proposition 3.1, we can construct an orientable 4–manifold M with
![]() $\pi _1(M)=G$
and
$\pi _1(M)=G$
and
![]() $\chi (M)=2$
. More generally, this can be done whenever
$\chi (M)=2$
. More generally, this can be done whenever
![]() $\mu _2(G) =1$
by Theorem B (see Corollary 3.9 and the series of groups
$\mu _2(G) =1$
by Theorem B (see Corollary 3.9 and the series of groups
![]() $J_k$
considered in Example 5.9). Then M is a rational homology 4–sphere, and in these cases, there is a minimal representative J for the stable module
$J_k$
considered in Example 5.9). Then M is a rational homology 4–sphere, and in these cases, there is a minimal representative J for the stable module
![]() $\Omega ^3(\mathbb Z)$
with
$\Omega ^3(\mathbb Z)$
with
![]() $\operatorname {\mathrm {rank}}_{\mathbb Z}(J) = |G|-1$
(compare [Reference Hambleton and Kreck13, Corollary 4.4]). For example, if G is the fundamental group of a closed, oriented
$\operatorname {\mathrm {rank}}_{\mathbb Z}(J) = |G|-1$
(compare [Reference Hambleton and Kreck13, Corollary 4.4]). For example, if G is the fundamental group of a closed, oriented
![]() $3$
-manifold, then
$3$
-manifold, then
![]() $J \cong I(G)^*$
.
$J \cong I(G)^*$
.
Remark 6.5. We are indebted to Mike Newman and Özgün Ünlü for showing that some of the groups
![]() $J_k$
do have deficiency zero (e.g. at least for
$J_k$
do have deficiency zero (e.g. at least for
![]() $3 \leq k \leq 6$
). It is a challenging, open problem to decide whether this is true for all
$3 \leq k \leq 6$
). It is a challenging, open problem to decide whether this is true for all
![]() $k \geq 3$
. Note that any group in this range which does not admit a balanced presentation would give a negative answer to Wall’s D2 problem.
$k \geq 3$
. Note that any group in this range which does not admit a balanced presentation would give a negative answer to Wall’s D2 problem.
Example 6.6. Teichner [Reference Teichner43, 3.4, 4.15] proved that if G is a finite
![]() $\mathbb Q S^4$
-group, then
$\mathbb Q S^4$
-group, then
![]() $d(H_1(G)) \leq 7$
, and used a mapping torus construction to produce a nonabelian
$d(H_1(G)) \leq 7$
, and used a mapping torus construction to produce a nonabelian
![]() $\mathbb Q S^4$
-group G with
$\mathbb Q S^4$
-group G with
![]() $d(H_1(G)) = 4$
.
$d(H_1(G)) = 4$
.
Section 6C. Algebraic questions. For the rational homology
![]() $4$
-spheres M with
$4$
-spheres M with
![]() $\pi _1(M)=G$
constructed in Theorem B, we have
$\pi _1(M)=G$
constructed in Theorem B, we have
![]() $\pi _2(M) = H_2(\widetilde M;\mathbb Z) = J \oplus J^*$
, where J is a minimal representative for
$\pi _2(M) = H_2(\widetilde M;\mathbb Z) = J \oplus J^*$
, where J is a minimal representative for
![]() $\Omega ^3(\mathbb Z)$
over
$\Omega ^3(\mathbb Z)$
over
![]() $\mathbb Z G$
, with
$\mathbb Z G$
, with
![]() $\operatorname {\mathrm {rank}}_{\mathbb Z}(J) = |G|-1$
.
$\operatorname {\mathrm {rank}}_{\mathbb Z}(J) = |G|-1$
.
Moreover, J is locally, and hence, rationally isomorphic to the augmentation ideal
![]() $I(G)$
, and the equivariant intersection form
$I(G)$
, and the equivariant intersection form
![]() $s_M$
on
$s_M$
on
![]() $\pi _2(M) = J \oplus J^*$
is metabolic, with totally isotropic submodule
$\pi _2(M) = J \oplus J^*$
is metabolic, with totally isotropic submodule
![]() $0 \oplus J^*$
. Similar results hold for the higher-dimensional examples constructed in Proposition 3.1.
$0 \oplus J^*$
. Similar results hold for the higher-dimensional examples constructed in Proposition 3.1.
More generally, for any finite group G, the existence of a representative J for the stable module
![]() $\Omega ^3(\mathbb Z)$
with
$\Omega ^3(\mathbb Z)$
with
![]() $\operatorname {\mathrm {rank}}_{\mathbb Z}(J) = |G|-1$
is equivalent to the condition
$\operatorname {\mathrm {rank}}_{\mathbb Z}(J) = |G|-1$
is equivalent to the condition
![]() $\mu _2(G) =1$
(see Proposition 3.7).
$\mu _2(G) =1$
(see Proposition 3.7).
Question. Is there a finite group G with
![]() $\mu _2(G) = 1$
, such that G is neither periodic nor admits a balanced presentation?
$\mu _2(G) = 1$
, such that G is neither periodic nor admits a balanced presentation?
For any closed, oriented
![]() $4$
-manifold M with finite fundamental group G, we have seen in 2.3 that
$4$
-manifold M with finite fundamental group G, we have seen in 2.3 that
![]() $\pi _2(M)$
is stably given by an extension of
$\pi _2(M)$
is stably given by an extension of
![]() $\Omega ^{-3}(\mathbb Z)$
by
$\Omega ^{-3}(\mathbb Z)$
by
![]() $\Omega ^3(\mathbb Z)$
(see also [Reference Hambleton and Kreck13, Proposition 2.4]) and that the extension class in
$\Omega ^3(\mathbb Z)$
(see also [Reference Hambleton and Kreck13, Proposition 2.4]) and that the extension class in
![]() $\operatorname {\mathrm {Ext}}^1_{\mathbb Z G}(\Omega ^{-3}(\mathbb Z), \Omega ^{3}(\mathbb Z)) \cong H_4(G; \mathbb Z)$
is given by the image of the fundamental class of M. For any rational homology
$\operatorname {\mathrm {Ext}}^1_{\mathbb Z G}(\Omega ^{-3}(\mathbb Z), \Omega ^{3}(\mathbb Z)) \cong H_4(G; \mathbb Z)$
is given by the image of the fundamental class of M. For any rational homology
![]() $4$
-sphere M with finite fundamental group G, the condition
$4$
-sphere M with finite fundamental group G, the condition
![]() $\chi (M) =2$
implies that
$\chi (M) =2$
implies that
![]() $\operatorname {\mathrm {rank}} _{\mathbb Z} (\pi _2(M)) = 2(|G| -1)$
and
$\operatorname {\mathrm {rank}} _{\mathbb Z} (\pi _2(M)) = 2(|G| -1)$
and
![]() $H^0(G; \pi _2(M)) = 0$
.
$H^0(G; \pi _2(M)) = 0$
.
Question. If M is a
![]() $\mathbb Q S^4$
, what is the (unstable) structure of
$\mathbb Q S^4$
, what is the (unstable) structure of
![]() $\pi _2(M)$
as an integral representation? Is the equivariant intersection form
$\pi _2(M)$
as an integral representation? Is the equivariant intersection form
![]() $s_M$
always metabolic (in the sense defined in [Reference Hambleton and Kreck14, Section 2])?
$s_M$
always metabolic (in the sense defined in [Reference Hambleton and Kreck14, Section 2])?
Finally, we point out that many questions in the representation theory of finite groups can be investigated by induction and restriction to proper subgroups. At present, we do not see how to apply this technique in our setting.
Question. If M is a
![]() $\mathbb Q S^4$
-manifold with finite fundamental group G, then its nontrivial finite coverings have Euler characteristic
$\mathbb Q S^4$
-manifold with finite fundamental group G, then its nontrivial finite coverings have Euler characteristic
![]() $> 2$
(and, hence, are not
$> 2$
(and, hence, are not
![]() $\mathbb Q S^4$
-manifolds). How can we decide if proper subgroups of G are also
$\mathbb Q S^4$
-manifolds). How can we decide if proper subgroups of G are also
![]() $\mathbb Q S^4$
-groups?
$\mathbb Q S^4$
-groups?
7 Appendix A: The Proof of Theorem 3.8
In this section, we give a direct construction of the minimal
![]() $4$
-manifold needed for Theorem 3.8. The idea is to use a handlebody thickening (see Definition 7.4) of a finite
$4$
-manifold needed for Theorem 3.8. The idea is to use a handlebody thickening (see Definition 7.4) of a finite
![]() $2$
-complex K instead of starting with an embedding of K in
$2$
-complex K instead of starting with an embedding of K in
![]() $\mathbb R^5$
. The advantage of this thickening is that we can identify the intersection form of its
$\mathbb R^5$
. The advantage of this thickening is that we can identify the intersection form of its
![]() $4$
-manifold boundary, and then apply a recent refinement of Freedman’s work due to Teichner, Powell and Ray (see [Reference Powell, Ray and Teichner35, Corollary 1.4]).
$4$
-manifold boundary, and then apply a recent refinement of Freedman’s work due to Teichner, Powell and Ray (see [Reference Powell, Ray and Teichner35, Corollary 1.4]).
Section 7A. Metabolic forms. To analyse the intersection form of the handlebody thickening, we will need some algebraic preparations.
Definition 7.1. Let
![]() $(E, [q])$
denote a quadratic metabolic form on a
$(E, [q])$
denote a quadratic metabolic form on a
![]() $\Lambda $
-module
$\Lambda $
-module
![]() $E = N \oplus N^*$
, where N is a left
$E = N \oplus N^*$
, where N is a left
![]() $\Lambda $
-module and
$\Lambda $
-module and
![]() $N^*$
inherits a left
$N^*$
inherits a left
![]() $\Lambda $
-module structure via the standard anti-involution
$\Lambda $
-module structure via the standard anti-involution
![]() $ a \mapsto \bar a$
on
$ a \mapsto \bar a$
on
![]() $\Lambda = \mathbb Z G$
. Then
$\Lambda = \mathbb Z G$
. Then
where
![]() $x, x' \in N$
,
$x, x' \in N$
,
![]() $\phi , \phi ' \in N^*$
and
$\phi , \phi ' \in N^*$
and
![]() $g \in \operatorname {\mathrm {Hom}}(N^* \otimes N^*, \Lambda )$
is a sesquilinear form. We use the notation
$g \in \operatorname {\mathrm {Hom}}(N^* \otimes N^*, \Lambda )$
is a sesquilinear form. We use the notation
![]() $(E, [q]) = \operatorname {\mathrm {Met}}(N, g)$
for this metabolic form (see [Reference Hambleton and Kreck14, Section 2] for metabolic forms defined on a nonsplit extension of N and
$(E, [q]) = \operatorname {\mathrm {Met}}(N, g)$
for this metabolic form (see [Reference Hambleton and Kreck14, Section 2] for metabolic forms defined on a nonsplit extension of N and
![]() $N^*$
).
$N^*$
).
The associated Hermitian form
![]() $h = q + q^*$
is nonsingular, and
$h = q + q^*$
is nonsingular, and
![]() $N \oplus 0 \subset E$
is a totally isotropic direct summand. More explicitly,
$N \oplus 0 \subset E$
is a totally isotropic direct summand. More explicitly,
In our geometric setting, the metabolic forms arise on modules
![]() $E = H^2(K) \oplus H_2(K)$
, where K is a finite
$E = H^2(K) \oplus H_2(K)$
, where K is a finite
![]() $2$
-complex with fundamental group G (take coefficients in
$2$
-complex with fundamental group G (take coefficients in
![]() $\Lambda = \mathbb Z G$
). If G is finite, then
$\Lambda = \mathbb Z G$
). If G is finite, then
![]() $H^2(K; \Lambda ) \cong \operatorname {\mathrm {Hom}}_{\Lambda }(H_2(K), \Lambda )$
, and the definition above applies. If G is infinite, then we slightly generalise our notion of metabolic form.
$H^2(K; \Lambda ) \cong \operatorname {\mathrm {Hom}}_{\Lambda }(H_2(K), \Lambda )$
, and the definition above applies. If G is infinite, then we slightly generalise our notion of metabolic form.
Definition 7.2. Let
![]() $E = N \oplus \widehat N$
, and let
$E = N \oplus \widehat N$
, and let
![]() $\alpha \colon \widehat N\to N^*$
be a
$\alpha \colon \widehat N\to N^*$
be a
![]() $\Lambda $
-module homomorphism. Define a generalised metabolic form
$\Lambda $
-module homomorphism. Define a generalised metabolic form
![]() $(E, [q]):= \operatorname {\mathrm {Met}}(N, \widehat N, \alpha , g)$
by the formula
$(E, [q]):= \operatorname {\mathrm {Met}}(N, \widehat N, \alpha , g)$
by the formula
where
![]() $x, x' \in N$
,
$x, x' \in N$
,
![]() $\phi , \phi ' \in \widehat N$
, and
$\phi , \phi ' \in \widehat N$
, and
![]() $g \in \operatorname {\mathrm {Hom}}(\widehat N \otimes \widehat N, \Lambda )$
is a given sesquilinear form.
$g \in \operatorname {\mathrm {Hom}}(\widehat N \otimes \widehat N, \Lambda )$
is a given sesquilinear form.
Example 7.3. For a finite
![]() $2$
-complex K, we have the evaluation map
$2$
-complex K, we have the evaluation map
![]() $\alpha \colon H^2(K) \to \operatorname {\mathrm {Hom}}_{\Lambda }(H_2(K), \Lambda )$
, which in general is neither injective nor surjective. In this case, we will shorten the notation of Definition 7.2 to
$\alpha \colon H^2(K) \to \operatorname {\mathrm {Hom}}_{\Lambda }(H_2(K), \Lambda )$
, which in general is neither injective nor surjective. In this case, we will shorten the notation of Definition 7.2 to
![]() $(E, [q]) =\operatorname {\mathrm {Met}}(H_2(K), g)$
, where
$(E, [q]) =\operatorname {\mathrm {Met}}(H_2(K), g)$
, where
![]() $E = H_2(K) \oplus H^2(K)$
as above.
$E = H_2(K) \oplus H^2(K)$
as above.
Here are some preliminary remarks.
-
• Let
 $(E, [q])$
be any quadratic form, and suppose that U is a finitely generated submodule on which the restriction
$(E, [q])$
be any quadratic form, and suppose that U is a finitely generated submodule on which the restriction
 $\lambda _0$
of
$\lambda _0$
of
 $\lambda = q + q*$
to U is nonsingular. Then there is is orthogonal splitting
$\lambda = q + q*$
to U is nonsingular. Then there is is orthogonal splitting
 $(E, [q]) \cong U \perp L$
.
$(E, [q]) \cong U \perp L$
.Proof. Consider the following sequence
 $$ \begin{align*}0 \to U \to E \xrightarrow{\operatorname{\mathrm{ad}} \lambda} E^* \to U^* \to 0,\end{align*} $$
$$ \begin{align*}0 \to U \to E \xrightarrow{\operatorname{\mathrm{ad}} \lambda} E^* \to U^* \to 0,\end{align*} $$
where the composition
 $\operatorname {\mathrm {ad}} \lambda _0\colon U \to U^*$
is an isomorphism by assumption. Therefore, the inclusion
$\operatorname {\mathrm {ad}} \lambda _0\colon U \to U^*$
is an isomorphism by assumption. Therefore, the inclusion
 $U \subset E$
is a split injection, and
$U \subset E$
is a split injection, and
 $E = U \perp L$
, where
$E = U \perp L$
, where
 $L := U^{\perp }$
. To check this last point, note that a splitting map for the inclusion
$L := U^{\perp }$
. To check this last point, note that a splitting map for the inclusion
 $i \colon U \to E$
is given by
$i \colon U \to E$
is given by  $$ \begin{align*}r := (\operatorname{\mathrm{ad}} \lambda_0)^{-1} \circ i^* \circ \operatorname{\mathrm{ad}} \lambda \circ i.\end{align*} $$
$$ \begin{align*}r := (\operatorname{\mathrm{ad}} \lambda_0)^{-1} \circ i^* \circ \operatorname{\mathrm{ad}} \lambda \circ i.\end{align*} $$
For
 $e \in E$
, we compute
$e \in E$
, we compute  $$ \begin{align*}\hphantom{xxxxx} \lambda(e - i(r(e)), i(h)) = \lambda (e, i(h)) - \lambda (i(r(e)), i(h)) = \lambda (e, i(h)) - \lambda_0(r(e), h) = 0\end{align*} $$
$$ \begin{align*}\hphantom{xxxxx} \lambda(e - i(r(e)), i(h)) = \lambda (e, i(h)) - \lambda (i(r(e)), i(h)) = \lambda (e, i(h)) - \lambda_0(r(e), h) = 0\end{align*} $$
after substituting the formula for r. Therefore,
 $E = U + U^{\perp }$
, and
$E = U + U^{\perp }$
, and
 $U \cap U^{\perp } = 0$
since
$U \cap U^{\perp } = 0$
since
 $\lambda _0$
is nonsingular.
$\lambda _0$
is nonsingular. -
• Let
 $(E, [q]) = \operatorname {\mathrm {Met}}(H,g)$
be a metabolic quadratic form on
$(E, [q]) = \operatorname {\mathrm {Met}}(H,g)$
be a metabolic quadratic form on
 $E = H\oplus H^*$
, where
$E = H\oplus H^*$
, where
 $H = \Lambda ^r$
is a finitely generated free
$H = \Lambda ^r$
is a finitely generated free
 $\Lambda $
-module. Then
$\Lambda $
-module. Then
 $(E, [q]) \cong H(\Lambda ^r)$
is a hyperbolic form.
$(E, [q]) \cong H(\Lambda ^r)$
is a hyperbolic form.Proof. This is a standard fact (see [Reference Wall and Ranicki50, Lemma 5.3]).
Section 7B. A handlebody thickening. Let K be a finite
![]() $2$
-complex with
$2$
-complex with
![]() $\pi _1(K) = G$
. We construct a suitable thickening of K to be used in the proof of Theorem 3.8.
$\pi _1(K) = G$
. We construct a suitable thickening of K to be used in the proof of Theorem 3.8.
Definition 7.4. We first consider a
![]() $4$
-dimensional parallelisable thickening
$4$
-dimensional parallelisable thickening
![]() $A(K)$
of K constructed by attaching suitable
$A(K)$
of K constructed by attaching suitable
![]() $2$
-handles to a connected sum
$2$
-handles to a connected sum
![]() $\operatorname {\mathrm {\sharp }} \ell (S^1\times D^3)$
. Then
$\operatorname {\mathrm {\sharp }} \ell (S^1\times D^3)$
. Then
![]() $A(K)$
is a compact
$A(K)$
is a compact
![]() $4$
-manifold with boundary, and we let
$4$
-manifold with boundary, and we let
![]() $N(K) = A(K) \times I$
. Note that
$N(K) = A(K) \times I$
. Note that
![]() $N(K)$
is a
$N(K)$
is a
![]() $5$
-dimensional thickening of K but may not embed in
$5$
-dimensional thickening of K but may not embed in
![]() $\mathbb R^5$
, and that
$\mathbb R^5$
, and that
![]() $\partial N(K) = A(K) \cup -A(K)$
is the double of A along the common boundary.
$\partial N(K) = A(K) \cup -A(K)$
is the double of A along the common boundary.
Then
![]() $ M:= \partial N(K)$
has the intersection form
$ M:= \partial N(K)$
has the intersection form
![]() $\lambda _M =\operatorname {\mathrm {Met}}(H_2(K), g)$
, since
$\lambda _M =\operatorname {\mathrm {Met}}(H_2(K), g)$
, since
![]() $H_2(\partial N(K)) = H^2(K) \oplus H_2(K)$
and the direct summand
$H_2(\partial N(K)) = H^2(K) \oplus H_2(K)$
and the direct summand
![]() $H^2(K)$
is totally isotropic (compare [Reference Kreck and Schafer24, Section 2]). All the homology groups have coefficients in
$H^2(K)$
is totally isotropic (compare [Reference Kreck and Schafer24, Section 2]). All the homology groups have coefficients in
![]() $\Lambda := \mathbb Z G$
.
$\Lambda := \mathbb Z G$
.
Remark 7.5. Note that the quadratic intersection form
![]() $\operatorname {\mathrm {Met}}(H_2(K), g)$
is a generalised metabolic form (see Example 7.3). It is nonsingular if
$\operatorname {\mathrm {Met}}(H_2(K), g)$
is a generalised metabolic form (see Example 7.3). It is nonsingular if
![]() $\pi _1(K) = G$
is a finite group. If G is infinite, this form has radical
$\pi _1(K) = G$
is a finite group. If G is infinite, this form has radical
![]() $H^2(G; \Lambda )$
, and the cokernel of its adjoint is
$H^2(G; \Lambda )$
, and the cokernel of its adjoint is
![]() $H^3(G; \Lambda )$
by the exact sequence
$H^3(G; \Lambda )$
by the exact sequence
arising from the universal coefficient theorem.
Section 7C. A self-homotopy equivalence. Let
![]() $N(K)_r := N(K) \natural \, r(S^2 \times D^3)$
denote this new thickening of
$N(K)_r := N(K) \natural \, r(S^2 \times D^3)$
denote this new thickening of
![]() $K \vee r(S^2)$
. We recall the construction of a useful homotopy self-equivalence of
$K \vee r(S^2)$
. We recall the construction of a useful homotopy self-equivalence of
![]() $K \vee r(S^2)$
.
$K \vee r(S^2)$
.
Lemma 7.6 [Reference Hambleton12, Lemma 2.1]
Let X be a finite
![]() $\mathrm {D2}$
-complex, and let
$\mathrm {D2}$
-complex, and let
![]() $u\colon K \subset X$
denote the
$u\colon K \subset X$
denote the
![]() $2$
-skeleton of X. Then, for
$2$
-skeleton of X. Then, for
![]() $r = b_3(X)$
, there is a simple self-homotopy equivalence
$r = b_3(X)$
, there is a simple self-homotopy equivalence
![]() $h \colon K \vee r(S^2) \to K \vee r(S^2)$
inducing a simple homotopy equivalence
$h \colon K \vee r(S^2) \to K \vee r(S^2)$
inducing a simple homotopy equivalence
![]() $f\colon X \vee r(S^2) \simeq K$
.
$f\colon X \vee r(S^2) \simeq K$
.
Proof. We recall some of the notation from [Reference Hambleton12, Section 2]. There is an identification
and we fix free
![]() $\Lambda $
-bases
$\Lambda $
-bases
![]() $\{e_1, \dots , e_r\}$
for
$\{e_1, \dots , e_r\}$
for
![]() $C_3(X) \cong \Lambda ^r$
and
$C_3(X) \cong \Lambda ^r$
and
![]() $\{f_1, \dots , f_r\}$
for
$\{f_1, \dots , f_r\}$
for
![]() $F \cong \Lambda ^r$
. The same notation
$F \cong \Lambda ^r$
. The same notation
![]() $\{e_i\}$
and
$\{e_i\}$
and
![]() $\{f_j\}$
will also be used for continuous maps
$\{f_j\}$
will also be used for continuous maps
![]() $S^2 \to K \vee r(S^2)$
in the homotopy classes of
$S^2 \to K \vee r(S^2)$
in the homotopy classes of
![]() $ \pi _2(K \vee r(S^2))$
defined by these basis elements. Notice that the maps
$ \pi _2(K \vee r(S^2))$
defined by these basis elements. Notice that the maps
![]() $f_j\colon S^2 \to K \vee r(S^2)$
may be chosen to represent the inclusions of the
$f_j\colon S^2 \to K \vee r(S^2)$
may be chosen to represent the inclusions of the
![]() $S^2$
wedge factors.
$S^2$
wedge factors.
An examination of the proof of [Reference Hambleton12, Lemma 2.1] shows that the simple homotopy equivalence
![]() $f\colon X \vee r(S^2) \simeq K$
is obtained by extending a certain simple homotopy equivalence
$f\colon X \vee r(S^2) \simeq K$
is obtained by extending a certain simple homotopy equivalence
![]() $h \colon K \vee r(S^2) \to K \vee r(S^2)$
over the (stabilised) inclusion
$h \colon K \vee r(S^2) \to K \vee r(S^2)$
over the (stabilised) inclusion

by attaching the
![]() $3$
-cells of X in domain by the maps
$3$
-cells of X in domain by the maps
![]() $e_i =[\partial D^3_i]$
,
$e_i =[\partial D^3_i]$
,
![]() $1\leq i \leq r$
, and
$1\leq i \leq r$
, and
![]() $3$
-cells in the range via the maps
$3$
-cells in the range via the maps
![]() $f_i =[\partial D^3_i]$
,
$f_i =[\partial D^3_i]$
,
![]() $1\leq i \leq r$
, which homotopically cancel the
$1\leq i \leq r$
, which homotopically cancel the
![]() $S^2$
wedge factors, to obtain a complex
$S^2$
wedge factors, to obtain a complex
![]() $K' \simeq K$
.
$K' \simeq K$
.
Then we have
![]() $h \circ [\partial D^3_i ]= f_i$
by the construction of h (see [Reference Hambleton12, p. 364]). Hence, we can extend h over X by the identity on the
$h \circ [\partial D^3_i ]= f_i$
by the construction of h (see [Reference Hambleton12, p. 364]). Hence, we can extend h over X by the identity on the
![]() $3$
-cells attached in domain and range along the maps
$3$
-cells attached in domain and range along the maps
![]() $\{f_i\colon S^2 \to K \vee r(S^2)\}$
. We obtain a map
$\{f_i\colon S^2 \to K \vee r(S^2)\}$
. We obtain a map
extending h. From the construction of the map h (see [Reference Hambleton12, p. 364]), it follows that
![]() $h'$
is a (simple) homotopy equivalence, which induces a simple homotopy equivalence
$h'$
is a (simple) homotopy equivalence, which induces a simple homotopy equivalence
![]() $f\colon X \vee r(S^2) \simeq K$
, after composition with the obvious projection
$f\colon X \vee r(S^2) \simeq K$
, after composition with the obvious projection
![]() $K' \to K$
.
$K' \to K$
.
Section 7D. Topological surgery. We will now apply some results of topological surgery due to Freedman. Recall that
![]() $N(K)$
is the
$N(K)$
is the
![]() $5$
-dimensional thickening of K constructed above and
$5$
-dimensional thickening of K constructed above and
![]() $N(K)_r = N(K) \natural \, r(S^2 \times D^3)$
is its stabilisation. We have introduced the notation
$N(K)_r = N(K) \natural \, r(S^2 \times D^3)$
is its stabilisation. We have introduced the notation
![]() $M = \partial N(K)$
, and let
$M = \partial N(K)$
, and let
![]() $M_r = \partial N(K)_r = \partial N(K) \# r(S^2 \times S^2)$
.
$M_r = \partial N(K)_r = \partial N(K) \# r(S^2 \times S^2)$
.
Lemma 7.7. Suppose that
![]() $\pi _1(K)$
is a good group. There is a self-homeomorphism
$\pi _1(K)$
is a good group. There is a self-homeomorphism
![]() $\beta \colon \partial N(K)_r \approx \partial N(K)_r$
extending the simple homotopy self-equivalence
$\beta \colon \partial N(K)_r \approx \partial N(K)_r$
extending the simple homotopy self-equivalence
![]() $h \colon K \vee r(S^2) \to K \vee r(S^2)$
.
$h \colon K \vee r(S^2) \to K \vee r(S^2)$
.
Proof. Since
![]() $\pi _1(K)$
is a good group, the topological s-cobordism theorem [Reference Freedman and Quinn9, Theorem 7.1A] implies that the given simple homotopy self-equivalence
$\pi _1(K)$
is a good group, the topological s-cobordism theorem [Reference Freedman and Quinn9, Theorem 7.1A] implies that the given simple homotopy self-equivalence
![]() $h \colon K \vee r(S^2) \to K \vee r(S^2)$
extends to a self-homeomorphism
$h \colon K \vee r(S^2) \to K \vee r(S^2)$
extends to a self-homeomorphism
![]() $\hat h \colon N(K)_r \to N(K)_r$
. This follows since we may assume (by general position) that the image
$\hat h \colon N(K)_r \to N(K)_r$
. This follows since we may assume (by general position) that the image
![]() $h( K \vee r(S^2)) \subset N(K))_r$
is embedded in the interior of the
$h( K \vee r(S^2)) \subset N(K))_r$
is embedded in the interior of the
![]() $5$
-manifold
$5$
-manifold
![]() $ N(K))_r$
. Since h is a simple homotopy self-equivalence, the complement of a small tubular neighbourhood of
$ N(K))_r$
. Since h is a simple homotopy self-equivalence, the complement of a small tubular neighbourhood of
![]() $h( K \vee r(S^2))$
will then be an s-cobordism, and hence, a product. Since
$h( K \vee r(S^2))$
will then be an s-cobordism, and hence, a product. Since
![]() $ N(K))_r$
is a thickening of
$ N(K))_r$
is a thickening of
![]() $K \vee r(S^2)$
, we can construct the self-homeomorphism
$K \vee r(S^2)$
, we can construct the self-homeomorphism
![]() $\hat h$
by identifying the tubular neighbourhoods in domain and range, and then using the product structures. Let
$\hat h$
by identifying the tubular neighbourhoods in domain and range, and then using the product structures. Let
![]() $\beta :=\partial \hat h$
denote the restriction of
$\beta :=\partial \hat h$
denote the restriction of
![]() $\hat h$
to
$\hat h$
to
![]() $\partial N(K)_r$
.
$\partial N(K)_r$
.
We now combine these ingredients. Recall that
![]() $X \vee r(S^2) \simeq K$
, so that
$X \vee r(S^2) \simeq K$
, so that
![]() $H_2(K) \cong H_2(X)\oplus H$
, where
$H_2(K) \cong H_2(X)\oplus H$
, where
![]() $H \cong \Lambda ^r$
. We have the isomorphism
$H \cong \Lambda ^r$
. We have the isomorphism
where
![]() $F\cong \Lambda ^r$
. We fix free
$F\cong \Lambda ^r$
. We fix free
![]() $\Lambda $
-bases
$\Lambda $
-bases
![]() $\{e_1, \dots , e_r\}$
for
$\{e_1, \dots , e_r\}$
for
![]() $H \cong \Lambda ^r$
, and
$H \cong \Lambda ^r$
, and
![]() $\{f_1, \dots , f_r\}$
for
$\{f_1, \dots , f_r\}$
for
![]() $F \cong \Lambda ^r$
. It follows that
$F \cong \Lambda ^r$
. It follows that
![]() $M_r := \partial N(K)_r$
has intersection form
$M_r := \partial N(K)_r$
has intersection form
where the classes
![]() $\{f_1, f_2, \dots , f_r\}$
and their duals provide a standard hyperbolic base for the second summand
$\{f_1, f_2, \dots , f_r\}$
and their duals provide a standard hyperbolic base for the second summand
![]() $H(F)$
. By construction,
$H(F)$
. By construction,
![]() $h_*(e_i) = f_i$
,
$h_*(e_i) = f_i$
,
![]() $h_*(f_i) = e_i$
for
$h_*(f_i) = e_i$
for
![]() $1 \leq i \leq r$
, and
$1 \leq i \leq r$
, and
![]() $h_*(x) = x$
for all
$h_*(x) = x$
for all
![]() $x \in H_2(X)$
. Note that
$x \in H_2(X)$
. Note that
![]() $H^2(K) = H^2(X)\oplus H^*$
is totally isotropic under
$H^2(K) = H^2(X)\oplus H^*$
is totally isotropic under
![]() $\lambda _M$
, and orthogonal to, the summand
$\lambda _M$
, and orthogonal to, the summand
![]() $H(F)$
.
$H(F)$
.
Lemma 7.8. There is a closed, topological
![]() $4$
-manifold
$4$
-manifold
![]() $M_0$
and a homeomorphism
$M_0$
and a homeomorphism
![]() $M_r = \partial N(K)_r \approx M_0 \operatorname {\mathrm {\sharp }} 2r(S^2 \times S^2)$
, such that
$M_r = \partial N(K)_r \approx M_0 \operatorname {\mathrm {\sharp }} 2r(S^2 \times S^2)$
, such that
![]() $\chi (M_0) = 2 \chi (X)$
.
$\chi (M_0) = 2 \chi (X)$
.
Proof. We have the decomposition:
in the notation introduced in (7.2).
The metabolic intersection form
![]() $\lambda _{M_r} = \lambda _{M} \oplus H(F)$
admits a self-isometry
$\lambda _{M_r} = \lambda _{M} \oplus H(F)$
admits a self-isometry
![]() $\beta _*$
(induced from the map
$\beta _*$
(induced from the map
![]() $\beta $
constructed in Lemma 7.7) extending the map
$\beta $
constructed in Lemma 7.7) extending the map
![]() $h_*\colon H_2(K) \oplus \Lambda ^r \to H_2(K) \oplus \Lambda ^r$
constructed above. Since the images of the basis elements
$h_*\colon H_2(K) \oplus \Lambda ^r \to H_2(K) \oplus \Lambda ^r$
constructed above. Since the images of the basis elements
![]() $h_*(e_i) = f_i \in F$
have dual classes
$h_*(e_i) = f_i \in F$
have dual classes
![]() $f^*_i \in F^*$
, it follows that
$f^*_i \in F^*$
, it follows that
Similarly, we have the formulas
and
Let
![]() $U = \langle \beta _*(F^*); H; F\oplus F^*\rangle $
denote the submodule of
$U = \langle \beta _*(F^*); H; F\oplus F^*\rangle $
denote the submodule of
![]() $H_2(M_r)$
generated by
$H_2(M_r)$
generated by
![]() $H(F) = F \oplus F^*$
, together with the classes
$H(F) = F \oplus F^*$
, together with the classes
![]() $\{\beta _*(f^*_i)\}$
, and the classes
$\{\beta _*(f^*_i)\}$
, and the classes
![]() $\{e_i\}$
, for
$\{e_i\}$
, for
![]() $1\leq i \leq r$
. Then we claim that
$1\leq i \leq r$
. Then we claim that
![]() $U \cong \beta _*(F^*) \oplus H \oplus H(F)$
is a free direct summand of
$U \cong \beta _*(F^*) \oplus H \oplus H(F)$
is a free direct summand of
![]() $H_2(M_r)$
, with indicated basis elements, on which the restriction of
$H_2(M_r)$
, with indicated basis elements, on which the restriction of
![]() $\lambda _{M_r}$
is a nonsingular form.
$\lambda _{M_r}$
is a nonsingular form.
We check that
![]() $U \cong \beta _*(F^*) \oplus H \oplus F\oplus F^*$
is a free submodule (of rank
$U \cong \beta _*(F^*) \oplus H \oplus F\oplus F^*$
is a free submodule (of rank
![]() $4r$
) in
$4r$
) in
![]() $H_2(M_r)$
by first showing that
$H_2(M_r)$
by first showing that
We then observe that the restriction
![]() $\lambda _U$
of the intersection form to
$\lambda _U$
of the intersection form to
![]() $U \subset H_2(M_r)$
is nonsingular. It follows that
$U \subset H_2(M_r)$
is nonsingular. It follows that
![]() $(U, \lambda _U)$
is an orthogonal direct summand of
$(U, \lambda _U)$
is an orthogonal direct summand of
![]() $(H_2(M_r), \lambda _{M_r})$
.
$(H_2(M_r), \lambda _{M_r})$
.
Here are the details: suppose that
![]() $u \in \beta _*(F^*) \cap (H \oplus F \oplus F^*)$
. We can express
$u \in \beta _*(F^*) \cap (H \oplus F \oplus F^*)$
. We can express
as
![]() $\Lambda $
-linear combinations of the basis elements. Then by the formula (7.3) above, we have
$\Lambda $
-linear combinations of the basis elements. Then by the formula (7.3) above, we have
![]() $ \lambda _{M_r}(\beta _*(f^*_i), e_j) = \delta _{ij}$
, and hence,
$ \lambda _{M_r}(\beta _*(f^*_i), e_j) = \delta _{ij}$
, and hence,
![]() $\lambda _{M_r}(u, e_i) = a_i$
. Since H is totally isotropic by (7.5), the summand
$\lambda _{M_r}(u, e_i) = a_i$
. Since H is totally isotropic by (7.5), the summand
![]() $H \oplus F \oplus F^*$
is orthogonal to H, and it follows that
$H \oplus F \oplus F^*$
is orthogonal to H, and it follows that
![]() $\lambda _{M_r}(u, e_i) = 0$
. Hence, all the
$\lambda _{M_r}(u, e_i) = 0$
. Hence, all the
![]() $a_i$
are zero and
$a_i$
are zero and
![]() $u=0$
.
$u=0$
.
Now let
![]() $\lambda _U$
denote the restriction of
$\lambda _U$
denote the restriction of
![]() $\lambda _{M_r}$
to U. The submodule
$\lambda _{M_r}$
to U. The submodule
![]() $H \oplus F$
is a totally isotropic-based free direct summand of rank
$H \oplus F$
is a totally isotropic-based free direct summand of rank
![]() $2r$
in U, and the dual basis elements under
$2r$
in U, and the dual basis elements under
![]() $\lambda _U$
form the basis of the complementary direct summand
$\lambda _U$
form the basis of the complementary direct summand
![]() $\beta _*(F^*) \oplus F^*$
. Hence,
$\beta _*(F^*) \oplus F^*$
. Hence,
![]() $\lambda _U$
is nonsingular, and in fact,
$\lambda _U$
is nonsingular, and in fact,
![]() $\lambda _U \cong \operatorname {\mathrm {Met}}(H \oplus F, g)$
, where g encodes the intersections of
$\lambda _U \cong \operatorname {\mathrm {Met}}(H \oplus F, g)$
, where g encodes the intersections of
![]() $\beta _*(F^*)$
with
$\beta _*(F^*)$
with
![]() $F^*$
(which may be nonzero). In this situation, it follows that
$F^*$
(which may be nonzero). In this situation, it follows that
![]() $\lambda _U \cong H(\Lambda ^{2r})$
is isomorphic to a nonsingular hyperbolic form (see [Reference Wall and Ranicki50, Lemma 5.3]).
$\lambda _U \cong H(\Lambda ^{2r})$
is isomorphic to a nonsingular hyperbolic form (see [Reference Wall and Ranicki50, Lemma 5.3]).
Hence, there is a splitting for the intersection form
with respect to the orthogonal complement
![]() $(E, \lambda _0)=(\lambda _U)^{\perp }$
. Since M has good fundamental group and
$(E, \lambda _0)=(\lambda _U)^{\perp }$
. Since M has good fundamental group and
![]() $\lambda _{M_r}$
contains the hyperbolic subform
$\lambda _{M_r}$
contains the hyperbolic subform
topological surgery [Reference Powell, Ray and Teichner35, Corollary 1.4] shows that
![]() $M \approx M_0 \operatorname {\mathrm {\sharp }} 2r(S^2 \times S^2)$
. The resulting closed, topological
$M \approx M_0 \operatorname {\mathrm {\sharp }} 2r(S^2 \times S^2)$
. The resulting closed, topological
![]() $4$
-manifold
$4$
-manifold
![]() $M_0$
has
$M_0$
has
![]() $\chi (M_0) = 2 \chi (X)$
.
$\chi (M_0) = 2 \chi (X)$
.
The construction of the manifold
![]() $M(X):= M_0$
completes the proof of Theorem 3.8.
$M(X):= M_0$
completes the proof of Theorem 3.8.
Acknowledgement
The authors would like to thank Mike Newman and Özgün Ünlü for showing that some of the finite groups G with
![]() $\mu _2(G) =1$
, considered in Example 5.9, do have deficiency zero. We would also like to thank the referee for many valuable comments. The second author was partially supported by a Natural Sciences and Engineering Research Council Discovery Grant.
$\mu _2(G) =1$
, considered in Example 5.9, do have deficiency zero. We would also like to thank the referee for many valuable comments. The second author was partially supported by a Natural Sciences and Engineering Research Council Discovery Grant.
Competing Interest
The authors have no competing interest to declare.