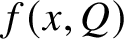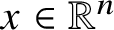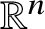1. Introduction
Sparse domination is a recent technique allowing one to estimate (in norm, pointwise or dually) many operators in harmonic analysis by simple expressions of the form
 $$ \begin{align*} \sum_{Q\in {\mathcal S}}\langle f\rangle_{p,Q}\chi_{Q},\\[-17pt] \end{align*} $$
$$ \begin{align*} \sum_{Q\in {\mathcal S}}\langle f\rangle_{p,Q}\chi_{Q},\\[-17pt] \end{align*} $$
where
 $\langle f\rangle _{p,Q}=\big (\frac {1}{|Q|}\int _{Q}|f|^{p}\big )^{1/p}$
for
$\langle f\rangle _{p,Q}=\big (\frac {1}{|Q|}\int _{Q}|f|^{p}\big )^{1/p}$
for
![]() $p \in (0,\infty )$
and
$p \in (0,\infty )$
and
![]() ${\mathcal S}$
is a sparse family of cubes in
${\mathcal S}$
is a sparse family of cubes in
![]() ${\mathbb R}^{n}$
.
${\mathbb R}^{n}$
.
Primarily motivated by sharp quantitative weighted norm inequalities, sparse domination has quickly transformed into a very active area, dealing with various operators within and beyond the Calderón–Zygmund theory. During the last five years, a number of sparse domination principles (that is, general results establishing sparse domination for a given class of operators) have appeared, for example, in the works [Reference Bailey, Brocchi and Reguera2, Reference Beltran, Roos and Seeger5, Reference Benea and Muscalu6, Reference Bernicot, Frey and Petermichl8, Reference Conde-Alonso, Culiuc, Di Plinio and Ou13, Reference Conde-Alonso, Di Plinio, Parissis and Vempati14, Reference Lerner34, Reference Lerner35, Reference Lerner and Ombrosi37, Reference Lorist39].
Let us consider a particular line of research in this direction, for which the starting point is the so-called local mean oscillation estimate (see [Reference Hytönen23, Reference Lerner31])
 $$ \begin{align} |f-m_{f}(Q)|\chi_{Q}\lesssim \sum_{P\in {\mathcal S}}\omega_{\lambda}(f;P)\chi_{P},\\[-17pt]\nonumber \end{align} $$
$$ \begin{align} |f-m_{f}(Q)|\chi_{Q}\lesssim \sum_{P\in {\mathcal S}}\omega_{\lambda}(f;P)\chi_{P},\\[-17pt]\nonumber \end{align} $$
where f is an arbitrary measurable function and
![]() $m_{f}(Q)$
and
$m_{f}(Q)$
and
![]() $\omega _{\lambda }(f;Q)$
denote a median value and the local mean oscillation of f on the cube Q, respectively.
$\omega _{\lambda }(f;Q)$
denote a median value and the local mean oscillation of f on the cube Q, respectively.
The local mean oscillation estimate can be regarded as the first operator-free sparse domination result, but its main application was to operators. Specifically, this estimate was applied by the first author in [Reference Lerner32] to a Calderón–Zygmund operator T, using
![]() $Tf$
instead of f in (1.1). This provided norm sparse domination for T and, as a result, an alternative proof of the
$Tf$
instead of f in (1.1). This provided norm sparse domination for T and, as a result, an alternative proof of the
![]() $A_{2}$
-theorem, which was first proven by Hytönen [Reference Hytönen22]. Later, this norm sparse domination result was improved to pointwise sparse domination simultaneously by Conde-Alonso–Rey and the first author and Nazarov in [Reference Conde-Alonso and Rey15, Reference Lerner and Nazarov36].
$A_{2}$
-theorem, which was first proven by Hytönen [Reference Hytönen22]. Later, this norm sparse domination result was improved to pointwise sparse domination simultaneously by Conde-Alonso–Rey and the first author and Nazarov in [Reference Conde-Alonso and Rey15, Reference Lerner and Nazarov36].
The methods in [Reference Conde-Alonso and Rey15, Reference Lerner and Nazarov36] still depended on (1.1). The drawback of this approach is that it necessitates estimating local mean oscillations of T, although T is not a well-localised operator. For this reason, the results in [Reference Conde-Alonso and Rey15, Reference Lerner and Nazarov36] hold under the
![]() $\log $
-Dini assumption on the kernel of the Calderón–Zygmund operator T.
$\log $
-Dini assumption on the kernel of the Calderón–Zygmund operator T.
The next step was taken by Lacey in [Reference Lacey30], where pointwise sparse domination for T was obtained under the usual Dini assumption on the kernel of T. The main new realisation in [Reference Lacey30] was that it suffices to estimate suitable truncations of T, which can be done without the use of (1.1). The proof of the pointwise sparse domination result for T was subsequently simplified by the first author in [Reference Lerner34] and the first and third authors in [Reference Lerner and Ombrosi37], in which a general sparse domination principle was established, allowing one to deal with a vast number of ‘smooth’ operators. The main result of [Reference Lerner and Ombrosi37] was then extended by the second author [Reference Lorist39] into several directions, including the setting of vector-valued functions on spaces of homogeneous type, along with the concept of
![]() $\ell ^{r}$
-sparse domination.
$\ell ^{r}$
-sparse domination.
The development we have so far described can be summarised in the following diagram:
Starting from [Reference Lacey30], the local mean oscillation estimate (1.1) has not played a role in the obtained sparse domination results. Therefore, this development can be viewed as an evolution from sparse domination for arbitrary functions (expressed in (1.1)) to sparse domination for operators.
In the present article, we return sparse domination to its roots, using functions rather than operators. We will essentially use the techniques developed in [Reference Lerner and Ombrosi37, Reference Lorist39]. Our key novel point is the language in which our main results are written. This language unifies (1.1) with all of the results contained in [Reference Lerner and Ombrosi37, Reference Lorist39]. More important, it allows us to deal with many non-operator objects, which have not yet been investigated using sparse domination techniques. This development can be seen in analogy to the development of Rubio de Francia extrapolation, which was first proven for operators but was later realised to be much more versatile and applicable in a formulation for functions (see [Reference Cruz-Uribe, Martell and Pérez16] for a discussion on this development).
Let us give a flavour of our language. Precise definitions and statements will be given in subsequent sections. We shall deal with functions
![]() $f(x,Q)$
of two ‘variables’, being the points
$f(x,Q)$
of two ‘variables’, being the points
![]() $x\in {\mathbb R}^{n}$
and the cubes
$x\in {\mathbb R}^{n}$
and the cubes
![]() $Q\subset {\mathbb R}^{n}$
. For brevity we denote such functions by
$Q\subset {\mathbb R}^{n}$
. For brevity we denote such functions by
![]() $f_{Q}(x)$
. Observe that the role of the cubes Q may vary. For example, one can define
$f_{Q}(x)$
. Observe that the role of the cubes Q may vary. For example, one can define
![]() $f_{Q}(x):=T(f\chi _{\alpha Q})(x)$
, where T is a given operator. On the other hand, in the theory of tent spaces, a typical definition will be
$f_{Q}(x):=T(f\chi _{\alpha Q})(x)$
, where T is a given operator. On the other hand, in the theory of tent spaces, a typical definition will be
 $f_{Q}(x):=\int _{\Gamma _{\ell _{Q}}(x)}f(y,t)\,\mathrm {d}\mu (y,t)$
, where
$f_{Q}(x):=\int _{\Gamma _{\ell _{Q}}(x)}f(y,t)\,\mathrm {d}\mu (y,t)$
, where
![]() $\Gamma _{\ell _{Q}}(x)$
is a cone in
$\Gamma _{\ell _{Q}}(x)$
is a cone in
![]() ${\mathbb R}^{n+1}_{+}$
, truncated according to the side length of Q.
${\mathbb R}^{n+1}_{+}$
, truncated according to the side length of Q.
Our main result, Theorem 3.2, provides pointwise sparse domination for
![]() $|f_{Q}|$
for a fixed cube
$|f_{Q}|$
for a fixed cube
![]() $Q \subset \mathbb {R}^{n}$
. The dominating sparse object is expressed in terms of
$Q \subset \mathbb {R}^{n}$
. The dominating sparse object is expressed in terms of
![]() $f_{P}$
for dyadic subcubes P of Q and a certain family of functions
$f_{P}$
for dyadic subcubes P of Q and a certain family of functions
![]() $f_{P,Q}$
, which connects
$f_{P,Q}$
, which connects
![]() $f_{P}$
and
$f_{P}$
and
![]() $f_{Q}$
in a natural way. A typical example is
$f_{Q}$
in a natural way. A typical example is
![]() $f_{P,Q}:=f_{Q}-f_{P}$
but, depending on the context, one can make more clever choices of
$f_{P,Q}:=f_{Q}-f_{P}$
but, depending on the context, one can make more clever choices of
![]() $f_{P,Q}$
.
$f_{P,Q}$
.
The article is organised as follows. Section 2 contains the main definitions. In particular, our language is introduced there. Section 3 contains our main results, which are pointwise and bilinear form operator-free sparse domination principles, expressed in Theorems 3.2 and 3.4. In Section 4 we show that our new results contain a vast number of previously known sparse domination results as particular cases.
Sections 5–8 present new applications. Section 5 is devoted to generalised Poincaré–Sobolev inequalities. In a recent work on this topic [Reference Pérez and Rela44], Pérez and Rela obtained a weighted self-improving result, assuming the
![]() $A_{\infty }$
-condition on the weight. They asked whether the
$A_{\infty }$
-condition on the weight. They asked whether the
![]() $A_{\infty }$
-condition can be removed. Using our sparse domination principle, we give an affirmative answer to this question.
$A_{\infty }$
-condition can be removed. Using our sparse domination principle, we give an affirmative answer to this question.
In Section 6, we give a ‘sparse’ proof of the theorem of Coifman–Meyer–Stein [Reference Coifman, Meyer and Stein11] on the main relation between two basic operators in the theory of tent spaces. In particular, this improves the good-
![]() $\lambda $
inequality for these operators established in [Reference Coifman, Meyer and Stein11]. We also obtain similar results for vector-valued tent spaces.
$\lambda $
inequality for these operators established in [Reference Coifman, Meyer and Stein11]. We also obtain similar results for vector-valued tent spaces.
In Section 7 we give a simplified proof of a recent result by Xu [Reference Xu48] about sharp bounds for the vector-valued vertical square function, which was an important ingredient in his answer to a question by Naor and Young [Reference Naor and Young43] about sharp bounds for the heat semigroup on
![]() ${\mathbb R}^{n}$
.
${\mathbb R}^{n}$
.
In Section 8 we obtain a simple sufficient condition allowing one, when dealing with the dyadic sums
![]() $\sum \alpha _{Q}\chi _{Q}$
, to replace the summation over all dyadic subcubes of a given cube by the summation over a sparse family. As an application, we will generalise and provide a new proof of a result by Honzík and Jaye [Reference Honzík and Jaye21] on a sharp good-
$\sum \alpha _{Q}\chi _{Q}$
, to replace the summation over all dyadic subcubes of a given cube by the summation over a sparse family. As an application, we will generalise and provide a new proof of a result by Honzík and Jaye [Reference Honzík and Jaye21] on a sharp good-
![]() $\lambda $
inequality for the nonlinear dyadic potential.
$\lambda $
inequality for the nonlinear dyadic potential.
Throughout the article we use the notation
![]() $A\lesssim B$
if
$A\lesssim B$
if
![]() $A\le CB$
with some independent constant C. We write
$A\le CB$
with some independent constant C. We write
![]() $A\eqsim B$
if
$A\eqsim B$
if
![]() $A\lesssim B$
and
$A\lesssim B$
and
![]() $B\lesssim A$
.
$B\lesssim A$
.
2. Main definitions
2.1. Dyadic cubes
Denote by
![]() ${\mathcal Q}$
the set of all cubes
${\mathcal Q}$
the set of all cubes
![]() $Q\subset {\mathbb R}^{n}$
with sides parallel to the axes. Given a cube
$Q\subset {\mathbb R}^{n}$
with sides parallel to the axes. Given a cube
![]() $Q\in {\mathcal Q}$
, denote by
$Q\in {\mathcal Q}$
, denote by
![]() ${\mathcal D}(Q)$
the set of all dyadic cubes with respect to Q; that is, the cubes obtained by repeated subdivision of Q and each of its descendants into
${\mathcal D}(Q)$
the set of all dyadic cubes with respect to Q; that is, the cubes obtained by repeated subdivision of Q and each of its descendants into
![]() $2^{n}$
congruent subcubes.
$2^{n}$
congruent subcubes.
Following [Reference Lerner and Nazarov36, Def. 2.1], a dyadic lattice
![]() ${\mathscr D}$
in
${\mathscr D}$
in
![]() ${\mathbb R}^{n}$
is any collection of cubes such that
${\mathbb R}^{n}$
is any collection of cubes such that
-
(i) any child of
 $Q\in {\mathscr D}$
is in
$Q\in {\mathscr D}$
is in
 ${\mathscr D}$
as well; that is,
${\mathscr D}$
as well; that is,
 $\mathcal {D}(Q) \subseteq \mathscr {D}$
,
$\mathcal {D}(Q) \subseteq \mathscr {D}$
, -
(ii) any
 $Q^{\prime },Q^{\prime \prime }\in {\mathscr D}$
have a common ancestor; that is, there exists a
$Q^{\prime },Q^{\prime \prime }\in {\mathscr D}$
have a common ancestor; that is, there exists a
 $Q\in {\mathscr D}$
such that
$Q\in {\mathscr D}$
such that
 $Q^{\prime },Q^{\prime \prime }\in {\mathcal D}(Q)$
,
$Q^{\prime },Q^{\prime \prime }\in {\mathcal D}(Q)$
, -
(iii) for every compact set
 $K\subset {\mathbb R}^{n}$
, there exists a cube
$K\subset {\mathbb R}^{n}$
, there exists a cube
 $Q\in {\mathscr D}$
containing K.
$Q\in {\mathscr D}$
containing K.
Let
![]() $Q\in {\mathcal Q}$
. We say that a family of dyadic cubes
$Q\in {\mathcal Q}$
. We say that a family of dyadic cubes
![]() ${\mathcal F}\subset {\mathcal D}(Q)$
is contracting if
${\mathcal F}\subset {\mathcal D}(Q)$
is contracting if
![]() ${\mathcal F}=\cup _{k=0}^{\infty }{\mathcal F}_{k}$
, where
${\mathcal F}=\cup _{k=0}^{\infty }{\mathcal F}_{k}$
, where
![]() $\mathcal {F}_{0} = \{ Q \}$
, each
$\mathcal {F}_{0} = \{ Q \}$
, each
![]() ${\mathcal F}_{k}$
is a family of pairwise disjoint cubes and for
${\mathcal F}_{k}$
is a family of pairwise disjoint cubes and for
![]() $\Omega _{k}=\cup _{P\in {\mathcal F}_{k}}P$
we have
$\Omega _{k}=\cup _{P\in {\mathcal F}_{k}}P$
we have
![]() $\Omega _{k+1}\subset \Omega _{k}$
and
$\Omega _{k+1}\subset \Omega _{k}$
and
![]() $|\Omega _{k}|\to 0$
as
$|\Omega _{k}|\to 0$
as
![]() $k\to \infty $
. Given a contracting family
$k\to \infty $
. Given a contracting family
![]() ${\mathcal F}\subset {\mathcal D}(Q)$
, for
${\mathcal F}\subset {\mathcal D}(Q)$
, for
![]() $P\in {\mathcal F}_{k}$
with
$P\in {\mathcal F}_{k}$
with
![]() $k\in \mathbb {N} \cup \{ 0 \},$
we denote
$k\in \mathbb {N} \cup \{ 0 \},$
we denote
 $$ \begin{align*} E_{P}:=P\setminus \bigcup_{P^{\prime}\in {\mathcal F}_{k+1}}P^{\prime} = P\setminus \Omega_{k+1}. \end{align*} $$
$$ \begin{align*} E_{P}:=P\setminus \bigcup_{P^{\prime}\in {\mathcal F}_{k+1}}P^{\prime} = P\setminus \Omega_{k+1}. \end{align*} $$
Observe that the sets
![]() $\{E_{P}\}_{P\in {\mathcal F}}$
are pairwise disjoint.
$\{E_{P}\}_{P\in {\mathcal F}}$
are pairwise disjoint.
Definition 2.1. Let
![]() $\eta \in (0,1)$
and
$\eta \in (0,1)$
and
![]() $Q \in \mathcal {Q}$
. We say that a family
$Q \in \mathcal {Q}$
. We say that a family
![]() ${\mathcal F}\subset {\mathcal D}(Q)$
is
${\mathcal F}\subset {\mathcal D}(Q)$
is
![]() $\eta $
-sparse if it is contracting and
$\eta $
-sparse if it is contracting and
![]() $|E_{P}|\ge \eta |P|$
for all
$|E_{P}|\ge \eta |P|$
for all
![]() $P\in {\mathcal F}$
.
$P\in {\mathcal F}$
.
Note that our definition of a sparse family of cubes is slightly more restrictive than the usual definition in the literature. In particular, we assume a sparse family of cubes to have exactly one maximal cube, the cube Q.
2.2. The
 $\ell ^{r}$
-condition
$\ell ^{r}$
-condition
Consider a family of measurable functions
![]() $\{f_{Q}, f_{P,Q}\}\colon {\mathbb R}^{n}\to {\mathbb R}$
, where
$\{f_{Q}, f_{P,Q}\}\colon {\mathbb R}^{n}\to {\mathbb R}$
, where
![]() $Q\in {\mathcal Q}$
,
$Q\in {\mathcal Q}$
,
![]() $P\in {\mathcal D}(Q)$
. We note that our choice of
$P\in {\mathcal D}(Q)$
. We note that our choice of
![]() $\mathbb {R}$
as the scalar field is inconsequential; that is, all subsequent results hold for complex-valued functions as well.
$\mathbb {R}$
as the scalar field is inconsequential; that is, all subsequent results hold for complex-valued functions as well.
We introduce a compatibility condition on such a family of functions, which is implicitly contained in [Reference Lorist39]. We will elaborate on the connection to [Reference Lorist39] in Subsection 4.2.
Definition 2.2. Let
![]() $r \in (0,\infty )$
. We say that the family
$r \in (0,\infty )$
. We say that the family
satisfies the
![]() $\ell ^{r}$
-condition if there exists a
$\ell ^{r}$
-condition if there exists a
![]() $C_{r}>0$
such that for every
$C_{r}>0$
such that for every
![]() $Q\in {\mathcal Q}$
and every
$Q\in {\mathcal Q}$
and every
![]() $P_{1},\dots , P_{m}\in {\mathcal D}(Q)$
with
$P_{1},\dots , P_{m}\in {\mathcal D}(Q)$
with
![]() $P_{m}\subset \dots \subset P_{1}$
, we have for a.e.
$P_{m}\subset \dots \subset P_{1}$
, we have for a.e.
![]() $x \in P_{m}$
,
$x \in P_{m}$
,
 $$ \begin{align*} |f_{P_{1}}(x)|\le C_{r}\Big(\sum_{k=1}^{m-1}|f_{P_{k+1},P_{k}}(x)|^{r}+|f_{P_{m}}(x)|^{r}\Big)^{1/r}. \end{align*} $$
$$ \begin{align*} |f_{P_{1}}(x)|\le C_{r}\Big(\sum_{k=1}^{m-1}|f_{P_{k+1},P_{k}}(x)|^{r}+|f_{P_{m}}(x)|^{r}\Big)^{1/r}. \end{align*} $$
Given an arbitrary family of measurable functions
![]() $f_{Q}\colon {\mathbb R}^{n}\to {\mathbb R}$
, a canonical choice for
$f_{Q}\colon {\mathbb R}^{n}\to {\mathbb R}$
, a canonical choice for
![]() $f_{P,Q}$
is given by
$f_{P,Q}$
is given by
for which the
![]() $\ell ^{r}$
-condition holds trivially with
$\ell ^{r}$
-condition holds trivially with
![]() $C_{r}=1$
for
$C_{r}=1$
for
![]() $0<r\le 1$
.
$0<r\le 1$
.
2.3. Sharp maximal operators
For a measurable function
![]() $f \colon \mathbb {R}^{n} \to \mathbb {R}$
, we define its standard oscillation over a cube
$f \colon \mathbb {R}^{n} \to \mathbb {R}$
, we define its standard oscillation over a cube
![]() $Q \in \mathcal {Q}$
by
$Q \in \mathcal {Q}$
by
 $$ \begin{align*} \operatorname{\mathrm{osc}}(f;Q)=\operatorname*{\mbox{ess sup}}_{x^{\prime},x^{\prime\prime}\in Q}|f(x^{\prime})-f(x^{\prime\prime})|. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{osc}}(f;Q)=\operatorname*{\mbox{ess sup}}_{x^{\prime},x^{\prime\prime}\in Q}|f(x^{\prime})-f(x^{\prime\prime})|. \end{align*} $$
Furthermore, for
![]() $q \in (0,\infty )$
, we define its q-oscillation over a cube
$q \in (0,\infty )$
, we define its q-oscillation over a cube
![]() $Q \in \mathcal {Q}$
by
$Q \in \mathcal {Q}$
by
 $$ \begin{align*} \operatorname{\mathrm{osc}}_{q}(f;Q)=\Big(\frac{1}{\lvert Q \rvert^{2}}\int_{Q\times Q}|f(x^{\prime})-f(x^{\prime\prime})|^{q}\,\mathrm{d} x^{\prime}\,\mathrm{d} x^{\prime\prime}\Big)^{1/q}. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{osc}}_{q}(f;Q)=\Big(\frac{1}{\lvert Q \rvert^{2}}\int_{Q\times Q}|f(x^{\prime})-f(x^{\prime\prime})|^{q}\,\mathrm{d} x^{\prime}\,\mathrm{d} x^{\prime\prime}\Big)^{1/q}. \end{align*} $$
Using these oscillations, we can now define sharp maximal operators associated to a family
![]() $\{f_{P,Q}\}$
, of which precursors can be found in [Reference Lerner and Ombrosi37, Reference Lorist39].
$\{f_{P,Q}\}$
, of which precursors can be found in [Reference Lerner and Ombrosi37, Reference Lorist39].
Definition 2.3. Given a family
![]() $\{f_{P,Q}\}_{Q\in {\mathcal Q}, P\in {\mathcal D}(Q)}$
, define the sharp maximal function
$\{f_{P,Q}\}_{Q\in {\mathcal Q}, P\in {\mathcal D}(Q)}$
, define the sharp maximal function
 $m_{Q}^{\#}f$
for
$m_{Q}^{\#}f$
for
![]() $Q \in \mathcal {Q}$
by
$Q \in \mathcal {Q}$
by
 $$ \begin{align*} m_{Q}^{\#}f(x)=\sup_{P\in {\mathcal D}(Q):x \in P}\operatorname{\mathrm{osc}}(f_{P,Q};P), \qquad x \in Q, \end{align*} $$
$$ \begin{align*} m_{Q}^{\#}f(x)=\sup_{P\in {\mathcal D}(Q):x \in P}\operatorname{\mathrm{osc}}(f_{P,Q};P), \qquad x \in Q, \end{align*} $$
and for
![]() $q \in (0,\infty )$
define the sharp q-maximal function by
$q \in (0,\infty )$
define the sharp q-maximal function by
 $$ \begin{align*} m_{Q,q}^{\#}f(x)=\sup_{P\in {\mathcal D}(Q):x \in P}\operatorname{\mathrm{osc}}_{q}(f_{P,Q};P)), \qquad x \in Q. \end{align*} $$
$$ \begin{align*} m_{Q,q}^{\#}f(x)=\sup_{P\in {\mathcal D}(Q):x \in P}\operatorname{\mathrm{osc}}_{q}(f_{P,Q};P)), \qquad x \in Q. \end{align*} $$
2.4. Nonincreasing rearrangements
The nonincreasing rearrangement of a measurable function
![]() $f \colon \mathbb {R}^{n} \to \mathbb {R}$
is defined by
$f \colon \mathbb {R}^{n} \to \mathbb {R}$
is defined by
 $$ \begin{align*} f^{*}(t)=\inf\big\{\alpha>0:|\{x\in {\mathbb R}^{n}:|f(x)|>\alpha\}|\le t\big\},\qquad t \in \mathbb{R}_{+}. \end{align*} $$
$$ \begin{align*} f^{*}(t)=\inf\big\{\alpha>0:|\{x\in {\mathbb R}^{n}:|f(x)|>\alpha\}|\le t\big\},\qquad t \in \mathbb{R}_{+}. \end{align*} $$
Observe that
![]() $(|f|^{\delta })^{*}(t)=f^{*}(t)^{\delta }$
for every
$(|f|^{\delta })^{*}(t)=f^{*}(t)^{\delta }$
for every
![]() $\delta>0$
. This, along with Chebyshev’s inequality
$\delta>0$
. This, along with Chebyshev’s inequality
 $f^{*}(t)\le \frac {1}{t}\|f\|_{L^{1}(\mathbb {R}^{n})}$
, implies that
$f^{*}(t)\le \frac {1}{t}\|f\|_{L^{1}(\mathbb {R}^{n})}$
, implies that
 $$ \begin{align} f^{*}(t)\le \frac{1}{t^{\frac1\delta}}\|f\|_{L^{\delta}(\mathbb{R}^{n})}. \end{align} $$
$$ \begin{align} f^{*}(t)\le \frac{1}{t^{\frac1\delta}}\|f\|_{L^{\delta}(\mathbb{R}^{n})}. \end{align} $$
We also have
 $$ \begin{align} \big|\{x\in {\mathbb R}^{n}:|f(x)|>f^{*}(t)\}\big|\le t, \end{align} $$
$$ \begin{align} \big|\{x\in {\mathbb R}^{n}:|f(x)|>f^{*}(t)\}\big|\le t, \end{align} $$
which is a consequence of the fact that the distribution function is right-continuous.
3. Main results
3.1. A toy domination principle
We start our analysis by observing that the
![]() $\ell ^{r}$
-condition allows us to bound
$\ell ^{r}$
-condition allows us to bound
![]() $f_{Q}$
for every
$f_{Q}$
for every
![]() $Q \in \mathcal {Q}$
by a sum over an arbitrary contracting family of cubes. In particular, we note that we do not need a sparseness assumption in the following statement.
$Q \in \mathcal {Q}$
by a sum over an arbitrary contracting family of cubes. In particular, we note that we do not need a sparseness assumption in the following statement.
Proposition 3.1. Let
![]() $r\in (0,\infty )$
and let
$r\in (0,\infty )$
and let
![]() $\{f_{Q},f_{P,Q}\}_{Q \in \mathcal {Q}, P \in \mathcal {D}(Q)}$
satisfy the
$\{f_{Q},f_{P,Q}\}_{Q \in \mathcal {Q}, P \in \mathcal {D}(Q)}$
satisfy the
![]() $\ell ^{r}$
-condition. Let
$\ell ^{r}$
-condition. Let
![]() $Q\in {\mathcal Q}$
and let
$Q\in {\mathcal Q}$
and let
![]() ${\mathcal F}\subset {\mathcal D}(Q)$
be a contracting family of cubes. Then for a.e.
${\mathcal F}\subset {\mathcal D}(Q)$
be a contracting family of cubes. Then for a.e.
![]() $x\in Q$
,
$x\in Q$
,
 $$ \begin{align*}|f_{Q}(x)|^{r}\le C_{r}^{r}\sum_{k=0}^{\infty}\sum_{P\in {\mathcal F}_{k}}\Big(|f_{P}(x)|^{r}\chi_{E_{P}}(x) +\sum_{P^{\prime}\in {\mathcal F}_{k+1}:P^{\prime}\subset P}|f_{P^{\prime},P}(x)|^{r}\chi_{P^{\prime}}(x)\Big). \end{align*} $$
$$ \begin{align*}|f_{Q}(x)|^{r}\le C_{r}^{r}\sum_{k=0}^{\infty}\sum_{P\in {\mathcal F}_{k}}\Big(|f_{P}(x)|^{r}\chi_{E_{P}}(x) +\sum_{P^{\prime}\in {\mathcal F}_{k+1}:P^{\prime}\subset P}|f_{P^{\prime},P}(x)|^{r}\chi_{P^{\prime}}(x)\Big). \end{align*} $$
Proof. Since
![]() $|\Omega _{k}|\to 0$
, there is a set
$|\Omega _{k}|\to 0$
, there is a set
![]() $N\subset Q$
of measure 0 such that, for every
$N\subset Q$
of measure 0 such that, for every
![]() $x\in Q\setminus N$
, there are only finitely many
$x\in Q\setminus N$
, there are only finitely many
![]() $k\in {\mathbb N}$
with
$k\in {\mathbb N}$
with
![]() $x\in \Omega _{k}$
.
$x\in \Omega _{k}$
.
Fix
![]() $x\in Q\setminus N$
. Then there exist
$x\in Q\setminus N$
. Then there exist
![]() $P_{k}\in {\mathcal F}_{k}$
for
$P_{k}\in {\mathcal F}_{k}$
for
![]() $k=0,\dots , m$
such that
$k=0,\dots , m$
such that
and
![]() $x\not \in \Omega _{m+1}$
. Hence, by the
$x\not \in \Omega _{m+1}$
. Hence, by the
![]() $\ell ^{r}$
-condition,
$\ell ^{r}$
-condition,
 $$ \begin{align*} |f_{Q}(x)|^{r}&\leq C_{r}^{r}\Big(|f_{P_{m}}(x)|^{r}+\sum_{k=0}^{m-1}|f_{P_{k+1},P_{k}}(x)|^{r}\Big)\\ &=C_{r}^{r}\Big(|f_{P_{m}}(x)|^{r}\chi_{E_{P_{m}}}(x)+\sum_{k=0}^{m-1}|f_{P_{k+1},P_{k}}(x)|^{r}\chi_{P_{k+1}}(x)\Big). \end{align*} $$
$$ \begin{align*} |f_{Q}(x)|^{r}&\leq C_{r}^{r}\Big(|f_{P_{m}}(x)|^{r}+\sum_{k=0}^{m-1}|f_{P_{k+1},P_{k}}(x)|^{r}\Big)\\ &=C_{r}^{r}\Big(|f_{P_{m}}(x)|^{r}\chi_{E_{P_{m}}}(x)+\sum_{k=0}^{m-1}|f_{P_{k+1},P_{k}}(x)|^{r}\chi_{P_{k+1}}(x)\Big). \end{align*} $$
In order to make this expression independent of the particular choice of
![]() $P_{k}$
, we add zero terms. This allows us to write
$P_{k}$
, we add zero terms. This allows us to write
 $$ \begin{align*} |f_{P_{m}}(x)|^{r}\chi_{E_{P_{m}}}(x)=\sum_{k=0}^{\infty}\sum_{P\in {\mathcal F}_{k}}|f_{P}(x)|^{r}\chi_{E_{P}}(x) \end{align*} $$
$$ \begin{align*} |f_{P_{m}}(x)|^{r}\chi_{E_{P_{m}}}(x)=\sum_{k=0}^{\infty}\sum_{P\in {\mathcal F}_{k}}|f_{P}(x)|^{r}\chi_{E_{P}}(x) \end{align*} $$
and
 $$ \begin{align*} \sum_{k=0}^{m-1}|f_{P_{k+1},P_{k}}(x)|^{r}\chi_{P_{k+1}}(x)=\sum_{k=0}^{\infty}\sum_{P\in {\mathcal F}_{k}}\sum_{P^{\prime}\in {\mathcal F}_{k+1}:P^{\prime}\subset P}|f_{P^{\prime},P}(x)|^{r}\chi_{P^{\prime}}(x), \end{align*} $$
$$ \begin{align*} \sum_{k=0}^{m-1}|f_{P_{k+1},P_{k}}(x)|^{r}\chi_{P_{k+1}}(x)=\sum_{k=0}^{\infty}\sum_{P\in {\mathcal F}_{k}}\sum_{P^{\prime}\in {\mathcal F}_{k+1}:P^{\prime}\subset P}|f_{P^{\prime},P}(x)|^{r}\chi_{P^{\prime}}(x), \end{align*} $$
which completes the proof.
3.2. A pointwise sparse domination principle
In order to estimate the terms
![]() $f_{P^{\prime },P}$
in Proposition 3.1 effectively, we make an additional assumption on the family
$f_{P^{\prime },P}$
in Proposition 3.1 effectively, we make an additional assumption on the family
![]() $\{f_{P,Q}\}_{Q\in {\mathcal Q}, P\in {\mathcal D}(Q)}$
. Indeed, we will assume for
$\{f_{P,Q}\}_{Q\in {\mathcal Q}, P\in {\mathcal D}(Q)}$
. Indeed, we will assume for
![]() $Q \in \mathcal {Q}$
and
$Q \in \mathcal {Q}$
and
![]() $P \in \mathcal {D}(Q)$
that
$P \in \mathcal {D}(Q)$
that
Observe that this assumption is not really restrictive. In particular, for the main example in (2.1), (3.1) holds trivially.
Our first main result is the following.
Theorem 3.2. Let
![]() $r \in (0,\infty )$
and let
$r \in (0,\infty )$
and let
![]() $\{f_{Q}, f_{P,Q}\}_{Q\in {\mathcal Q}, P\in {\mathcal D}(Q)}$
satisfy the
$\{f_{Q}, f_{P,Q}\}_{Q\in {\mathcal Q}, P\in {\mathcal D}(Q)}$
satisfy the
![]() $\ell ^{r}$
-condition and (3.1). For any
$\ell ^{r}$
-condition and (3.1). For any
![]() $Q \in \mathcal {Q}$
and
$Q \in \mathcal {Q}$
and
![]() $\eta \in (0,1)$
there exists an
$\eta \in (0,1)$
there exists an
![]() $\eta $
-sparse family
$\eta $
-sparse family
![]() ${\mathcal F}\subset \mathcal {D}(Q)$
such that for a.e.
${\mathcal F}\subset \mathcal {D}(Q)$
such that for a.e.
![]() $x\in Q$
,
$x\in Q$
,
 $$ \begin{align*} |f_{Q}(x)|\lesssim C_{r}\Big(\sum_{P\in {\mathcal F}}\gamma_{P}^{r}\chi_{P}(x)\Big)^{1/r}, \end{align*} $$
$$ \begin{align*} |f_{Q}(x)|\lesssim C_{r}\Big(\sum_{P\in {\mathcal F}}\gamma_{P}^{r}\chi_{P}(x)\Big)^{1/r}, \end{align*} $$
where
 $$ \begin{align*} \gamma_{P}:=(f_{P}\chi_{P})^{*}\big(|P|\tfrac{1-\eta}{2^{n+2}}\big)+(m^{\#}_{P}f)^{*}\big(|P|\tfrac{1-\eta}{2^{n+2}}\big). \end{align*} $$
$$ \begin{align*} \gamma_{P}:=(f_{P}\chi_{P})^{*}\big(|P|\tfrac{1-\eta}{2^{n+2}}\big)+(m^{\#}_{P}f)^{*}\big(|P|\tfrac{1-\eta}{2^{n+2}}\big). \end{align*} $$
Proof. We construct the family
![]() ${\mathcal F}\subset \mathcal {D}(Q)$
inductively. Set
${\mathcal F}\subset \mathcal {D}(Q)$
inductively. Set
![]() ${\mathcal F}_{0}=\{Q\}$
. Next, given a collection of pairwise disjoint cubes
${\mathcal F}_{0}=\{Q\}$
. Next, given a collection of pairwise disjoint cubes
![]() ${\mathcal F}_{k}$
, let us describe how to construct
${\mathcal F}_{k}$
, let us describe how to construct
![]() ${\mathcal F}_{k+1}$
.
${\mathcal F}_{k+1}$
.
Fix a cube
![]() $P\in {\mathcal F}_{k}$
. Consider the sets
$P\in {\mathcal F}_{k}$
. Consider the sets
 $$ \begin{align*} \Omega_{1}(P)&:=\big\{x\in P:|f_{P}(x)|>(f_{P}\chi_{P})^{*}\big(|P|\tfrac{1-\eta}{2^{n+2}}\big)\big\},\\ \Omega_{2}(P)&:=\big\{x\in P:m_{P}^{\#}f(x)>\big(m_{P}^{\#}f\big)^{*}\big(|P|\tfrac{1-\eta}{2^{n+2}}\big)\big\}, \end{align*} $$
$$ \begin{align*} \Omega_{1}(P)&:=\big\{x\in P:|f_{P}(x)|>(f_{P}\chi_{P})^{*}\big(|P|\tfrac{1-\eta}{2^{n+2}}\big)\big\},\\ \Omega_{2}(P)&:=\big\{x\in P:m_{P}^{\#}f(x)>\big(m_{P}^{\#}f\big)^{*}\big(|P|\tfrac{1-\eta}{2^{n+2}}\big)\big\}, \end{align*} $$
and denote
![]() $\Omega (P):=\Omega _{1}(P)\cup \Omega _{2}(P)$
. Then, by (2.3), we know that
$\Omega (P):=\Omega _{1}(P)\cup \Omega _{2}(P)$
. Then, by (2.3), we know that
 $|\Omega (P)|\le \frac {1-\eta }{2^{n+1}}|P|$
.
$|\Omega (P)|\le \frac {1-\eta }{2^{n+1}}|P|$
.
Apply the local Calderón–Zygmund decomposition to
![]() $\chi _{\Omega (P)}$
at height
$\chi _{\Omega (P)}$
at height
 $\frac {1}{2^{n+1}}$
. We obtain a family of pairwise disjoint cubes
$\frac {1}{2^{n+1}}$
. We obtain a family of pairwise disjoint cubes
![]() $\mathcal {S}_{P}=\{P_{j}\}$
, dyadic with respect to P, such that for
$\mathcal {S}_{P}=\{P_{j}\}$
, dyadic with respect to P, such that for
![]() $N_{P}=\Omega (P)\setminus \cup _{j}P_{j}$
we have that
$N_{P}=\Omega (P)\setminus \cup _{j}P_{j}$
we have that
![]() $|N_{P}|=0$
and for every
$|N_{P}|=0$
and for every
![]() $P_{j}\in \mathcal {S}_{P}$
,
$P_{j}\in \mathcal {S}_{P}$
,
 $$ \begin{align} \frac{1}{2^{n+1}}|P_{j}|\le |P_{j}\cap\Omega(P)|\le \frac{1}{2}|P_{j}|. \end{align} $$
$$ \begin{align} \frac{1}{2^{n+1}}|P_{j}|\le |P_{j}\cap\Omega(P)|\le \frac{1}{2}|P_{j}|. \end{align} $$
In particular, it follows from this that
 $$ \begin{align} \sum_{j}|P_{j}|\le 2^{n+1}|\Omega(P)|\le (1-\eta) |P|. \end{align} $$
$$ \begin{align} \sum_{j}|P_{j}|\le 2^{n+1}|\Omega(P)|\le (1-\eta) |P|. \end{align} $$
We define
![]() ${\mathcal F}_{k+1}=\cup _{P\in {\mathcal F}_{k}}\mathcal {S}_{P}$
. Setting
${\mathcal F}_{k+1}=\cup _{P\in {\mathcal F}_{k}}\mathcal {S}_{P}$
. Setting
![]() ${\mathcal F}=\cup _{k=0}^{\infty }{\mathcal F}_{k}$
, we note by (3.3) that
${\mathcal F}=\cup _{k=0}^{\infty }{\mathcal F}_{k}$
, we note by (3.3) that
![]() ${\mathcal F}$
is
${\mathcal F}$
is
![]() $\eta $
-sparse.
$\eta $
-sparse.
Let us now prepare to apply Proposition 3.1 with the constructed family
![]() ${\mathcal F}$
. Fix
${\mathcal F}$
. Fix
![]() $P\in {\mathcal F}_{k}$
for some
$P\in {\mathcal F}_{k}$
for some
![]() $k \in \mathbb {N} \cup \{ 0 \}$
. Since
$k \in \mathbb {N} \cup \{ 0 \}$
. Since
![]() $\lvert N_{P} \rvert =0$
, almost every point of the set
$\lvert N_{P} \rvert =0$
, almost every point of the set
![]() $\Omega _{1}(P)$
is covered by a cube
$\Omega _{1}(P)$
is covered by a cube
![]() $P^{\prime }\in {\mathcal F}_{k+1}$
. Therefore, we have
$P^{\prime }\in {\mathcal F}_{k+1}$
. Therefore, we have
 $$ \begin{align} |f_{P}(x)|\le (f_{P}\chi_{P})^{*}\big(|P|\tfrac{1-\eta}{2^{n+2}}\big), \qquad x \in E_{P}.\\[-15pt]\nonumber \end{align} $$
$$ \begin{align} |f_{P}(x)|\le (f_{P}\chi_{P})^{*}\big(|P|\tfrac{1-\eta}{2^{n+2}}\big), \qquad x \in E_{P}.\\[-15pt]\nonumber \end{align} $$
It remains to estimate
![]() $|f_{P^{\prime },P}|\chi _{P^{\prime }}$
for
$|f_{P^{\prime },P}|\chi _{P^{\prime }}$
for
![]() $P\in {\mathcal F}_{k}$
and
$P\in {\mathcal F}_{k}$
and
![]() $P^{\prime }\in {\mathcal F}_{k+1}$
with
$P^{\prime }\in {\mathcal F}_{k+1}$
with
![]() $P^{\prime }\subset P$
. Denote
$P^{\prime }\subset P$
. Denote
![]() $G_{P^{\prime }}=P^{\prime }\setminus \Omega (P)$
. Then, by (3.2), we have
$G_{P^{\prime }}=P^{\prime }\setminus \Omega (P)$
. Then, by (3.2), we have
 $$ \begin{align*} |G_{P^{\prime}}|\ge \lvert P^{\prime} \rvert - \lvert P^{\prime}\cap \Omega(P) \rvert \geq \frac12|P^{\prime}|.\\[-15pt] \end{align*} $$
$$ \begin{align*} |G_{P^{\prime}}|\ge \lvert P^{\prime} \rvert - \lvert P^{\prime}\cap \Omega(P) \rvert \geq \frac12|P^{\prime}|.\\[-15pt] \end{align*} $$
Therefore,
![]() $|G_{P^{\prime }}\setminus \Omega (P^{\prime })|>0$
and hence, fixing
$|G_{P^{\prime }}\setminus \Omega (P^{\prime })|>0$
and hence, fixing
and applying (3.1), we obtain for a.e.
![]() $x\in P^{\prime }$
$x\in P^{\prime }$
 $$ \begin{align*} |f_{P^{\prime},P}(x)|&\le \inf_{x^{\prime} \in P^{\prime}}m^{\#}_{P}f(x^{\prime})+|f_{P^{\prime},P}(y)|\\ &\le \big(m_{P}^{\#}f\big)^{*}\big(|P|\tfrac{1-\eta}{2^{n+2}}\big)+|f_{P}(y)|+|f_{P^{\prime}}(y)|\\ &\le \gamma_{P}+(f_{P^{\prime}}\chi_{P^{\prime}})^{*}\big(|P^{\prime}|\tfrac{1-\eta}{2^{n+2}}\big).\\[-15pt] \end{align*} $$
$$ \begin{align*} |f_{P^{\prime},P}(x)|&\le \inf_{x^{\prime} \in P^{\prime}}m^{\#}_{P}f(x^{\prime})+|f_{P^{\prime},P}(y)|\\ &\le \big(m_{P}^{\#}f\big)^{*}\big(|P|\tfrac{1-\eta}{2^{n+2}}\big)+|f_{P}(y)|+|f_{P^{\prime}}(y)|\\ &\le \gamma_{P}+(f_{P^{\prime}}\chi_{P^{\prime}})^{*}\big(|P^{\prime}|\tfrac{1-\eta}{2^{n+2}}\big).\\[-15pt] \end{align*} $$
Combining this estimate with (3.4) and Proposition 3.1 yields for a.e.
![]() $x\in Q$
that
$x\in Q$
that
 $$ \begin{align*} |f_{Q}(x)|^{r}&\le C_{r}^{r}\sum_{k=0}^{\infty}\sum_{P\in {\mathcal F}_{k}}\Big((f_{P}\chi_{P})^{*}\big(|P|\tfrac{1-\eta}{2^{n+2}}\big)^{r}\chi_{E_{P}}(x)\\ &\qquad\quad +\sum_{P^{\prime}\in {\mathcal F}_{k+1}:P^{\prime}\subset P}\big(\gamma_{P}+(f_{P^{\prime}}\chi_{P^{\prime}})^{*}\big(|P^{\prime}|\tfrac{1-\eta}{2^{n+2}}\big)\big)^{r}\chi_{P^{\prime}}(x)\Big)\\ &\le 2(2C_{r})^{r}\sum_{k=0}^{\infty}\sum_{P\in {\mathcal F}_{k}}\gamma_{P}^{r}\chi_{P}+(2C_{r})^{r}\sum_{k=0}^{\infty}\sum_{P\in {\mathcal F}_{k}}\sum_{P^{\prime}\in {\mathcal F}_{k+1}:P^{\prime}\subset P}\gamma_{P^{\prime}}^{r}\chi_{P^{\prime}}\\ &\le 3(2C_{r})^{r}\sum_{P\in {\mathcal F}}\gamma_{P}^{r}\chi_{P},\\[-15pt] \end{align*} $$
$$ \begin{align*} |f_{Q}(x)|^{r}&\le C_{r}^{r}\sum_{k=0}^{\infty}\sum_{P\in {\mathcal F}_{k}}\Big((f_{P}\chi_{P})^{*}\big(|P|\tfrac{1-\eta}{2^{n+2}}\big)^{r}\chi_{E_{P}}(x)\\ &\qquad\quad +\sum_{P^{\prime}\in {\mathcal F}_{k+1}:P^{\prime}\subset P}\big(\gamma_{P}+(f_{P^{\prime}}\chi_{P^{\prime}})^{*}\big(|P^{\prime}|\tfrac{1-\eta}{2^{n+2}}\big)\big)^{r}\chi_{P^{\prime}}(x)\Big)\\ &\le 2(2C_{r})^{r}\sum_{k=0}^{\infty}\sum_{P\in {\mathcal F}_{k}}\gamma_{P}^{r}\chi_{P}+(2C_{r})^{r}\sum_{k=0}^{\infty}\sum_{P\in {\mathcal F}_{k}}\sum_{P^{\prime}\in {\mathcal F}_{k+1}:P^{\prime}\subset P}\gamma_{P^{\prime}}^{r}\chi_{P^{\prime}}\\ &\le 3(2C_{r})^{r}\sum_{P\in {\mathcal F}}\gamma_{P}^{r}\chi_{P},\\[-15pt] \end{align*} $$
which completes the proof.
Remark 3.3. It is easily seen from the proof that Theorem 3.2 can be stated in a (formally stronger) local version. Namely, fix a cube
![]() $Q_{0}\in {\mathcal Q}$
, and assume that the
$Q_{0}\in {\mathcal Q}$
, and assume that the
![]() $\ell ^{r}$
-condition and (3.1) hold for a family of functions
$\ell ^{r}$
-condition and (3.1) hold for a family of functions
![]() $\{f_{Q},f_{P,Q}\}$
, where
$\{f_{Q},f_{P,Q}\}$
, where
![]() $P,Q\in {\mathcal D}(Q_{0})$
and
$P,Q\in {\mathcal D}(Q_{0})$
and
![]() $P\subseteq Q$
. Then for any
$P\subseteq Q$
. Then for any
![]() $\eta \in (0,1)$
there exists an
$\eta \in (0,1)$
there exists an
![]() $\eta $
-sparse family
$\eta $
-sparse family
![]() ${\mathcal F}\subset \mathcal {D}(Q_{0})$
such that for a.e.
${\mathcal F}\subset \mathcal {D}(Q_{0})$
such that for a.e.
![]() $x\in Q_{0}$
,
$x\in Q_{0}$
,
 $$ \begin{align*} |f_{Q_{0}}(x)|\lesssim C_{r}\Big(\sum_{P\in {\mathcal F}}\gamma_{P}^{r}\chi_{P}(x)\Big)^{1/r}\\[-15pt] \end{align*} $$
$$ \begin{align*} |f_{Q_{0}}(x)|\lesssim C_{r}\Big(\sum_{P\in {\mathcal F}}\gamma_{P}^{r}\chi_{P}(x)\Big)^{1/r}\\[-15pt] \end{align*} $$
with the same
![]() $\gamma _{P}$
as in Theorem 3.2. In particular, the family of all cubes
$\gamma _{P}$
as in Theorem 3.2. In particular, the family of all cubes
![]() ${\mathcal Q}$
in Theorem 3.2 can be replaced by an arbitrary subfamily; for example, by a dyadic lattice
${\mathcal Q}$
in Theorem 3.2 can be replaced by an arbitrary subfamily; for example, by a dyadic lattice
![]() ${\mathscr D}$
.
${\mathscr D}$
.
3.3. A bilinear form sparse domination principle
In certain applications the
 $m^{\#}_{Q}f$
-term in the definition of
$m^{\#}_{Q}f$
-term in the definition of
![]() $\gamma _{Q}$
in Theorem 3.2 is too large to be efficiently estimated. We will therefore also prove a variant of Theorem 3.2, dominating
$\gamma _{Q}$
in Theorem 3.2 is too large to be efficiently estimated. We will therefore also prove a variant of Theorem 3.2, dominating
![]() $|f_{Q}|$
dually by a sparse form involving the smaller term
$|f_{Q}|$
dually by a sparse form involving the smaller term
 $m^{\#}_{Q,q}f$
for
$m^{\#}_{Q,q}f$
for
![]() $q \in (0,\infty )$
.
$q \in (0,\infty )$
.
Theorem 3.4. Let
![]() $r \in (0,\infty )$
and let
$r \in (0,\infty )$
and let
![]() $\{f_{Q}, f_{P,Q}\}_{Q\in {\mathcal Q}, P\in {\mathcal D}(Q)}$
satisfy the
$\{f_{Q}, f_{P,Q}\}_{Q\in {\mathcal Q}, P\in {\mathcal D}(Q)}$
satisfy the
![]() $\ell ^{r}$
-condition and (3.1) and let
$\ell ^{r}$
-condition and (3.1) and let
![]() $q \in (r,\infty )$
. For any
$q \in (r,\infty )$
. For any
![]() $Q \in \mathcal {Q}$
and
$Q \in \mathcal {Q}$
and
![]() $\eta \in (0,1)$
there exists an
$\eta \in (0,1)$
there exists an
![]() $\eta $
-sparse family
$\eta $
-sparse family
![]() ${\mathcal F}\subset {\mathcal D}(Q)$
such that for every measurable
${\mathcal F}\subset {\mathcal D}(Q)$
such that for every measurable
![]() $g \colon \mathbb {R}^{n} \to \mathbb {R}_{+}$
,
$g \colon \mathbb {R}^{n} \to \mathbb {R}_{+}$
,
 $$ \begin{align*} \int_{Q}|f_{Q}|^{r}g\lesssim C_{r}\sum_{P\in {\mathcal F}}\alpha_{P}^{r}\langle g\rangle_{(q/r)^{\prime},P} |P|, \end{align*} $$
$$ \begin{align*} \int_{Q}|f_{Q}|^{r}g\lesssim C_{r}\sum_{P\in {\mathcal F}}\alpha_{P}^{r}\langle g\rangle_{(q/r)^{\prime},P} |P|, \end{align*} $$
where
 $$ \begin{align*} \alpha_{P}=(f_{P}\chi_{P})^{*}\big(\lvert P \rvert\tfrac{1-\eta}{2^{n+2}}\big)+(m^{\#}_{P,q}f)^{*}\big(\lvert P \rvert\tfrac{1-\eta}{2^{n+2}}\big). \end{align*} $$
$$ \begin{align*} \alpha_{P}=(f_{P}\chi_{P})^{*}\big(\lvert P \rvert\tfrac{1-\eta}{2^{n+2}}\big)+(m^{\#}_{P,q}f)^{*}\big(\lvert P \rvert\tfrac{1-\eta}{2^{n+2}}\big). \end{align*} $$
Proof. The proof is similar to the proof of Theorem 3.2 and hence some details are omitted. Construct the
![]() $\eta $
-sparse family
$\eta $
-sparse family
![]() ${\mathcal F}$
exactly as in the proof of Theorem 3.2, only replacing
${\mathcal F}$
exactly as in the proof of Theorem 3.2, only replacing
 $m_{P}^{\#}f$
by
$m_{P}^{\#}f$
by
 $m_{P,q}^{\#}f$
in the definition of
$m_{P,q}^{\#}f$
in the definition of
![]() $\Omega _{2}(P)$
.
$\Omega _{2}(P)$
.
By Proposition 3.1 we have
 $$ \begin{align} \int_{Q}|f_{Q}|^{r}g\le C_{r}^{r}\sum_{k=0}^{\infty}\sum_{P\in {\mathcal F}_{k}} \Big(\int_{E_{P}}|f_{P}|^{r}g+\sum_{\substack{P^{\prime}\in {\mathcal F}_{k+1}:\\P^{\prime}\subset P}}\int_{P^{\prime}}|f_{P^{\prime},P}|^{r}g\Big), \end{align} $$
$$ \begin{align} \int_{Q}|f_{Q}|^{r}g\le C_{r}^{r}\sum_{k=0}^{\infty}\sum_{P\in {\mathcal F}_{k}} \Big(\int_{E_{P}}|f_{P}|^{r}g+\sum_{\substack{P^{\prime}\in {\mathcal F}_{k+1}:\\P^{\prime}\subset P}}\int_{P^{\prime}}|f_{P^{\prime},P}|^{r}g\Big), \end{align} $$
and by (3.4)
 $$ \begin{align} \int_{E_{P}}|f_{P}|^{r}g\le \alpha_{P}^{r}\int_{P}g. \end{align} $$
$$ \begin{align} \int_{E_{P}}|f_{P}|^{r}g\le \alpha_{P}^{r}\int_{P}g. \end{align} $$
It remains to estimate the second term on the right-hand side of (3.5). As in the proof of Theorem 3.2, we introduce the set
![]() $G_{P^{\prime }}=P^{\prime }\setminus \Omega (P)$
and observe that
$G_{P^{\prime }}=P^{\prime }\setminus \Omega (P)$
and observe that
 $$ \begin{align} |G_{P^{\prime}}\setminus\Omega(P^{\prime})|\ge \Big(\frac{1}{2}-\frac{1}{2^{n+3}}\Big)|P^{\prime}|\ge \frac{1}{4}|P^{\prime}|. \end{align} $$
$$ \begin{align} |G_{P^{\prime}}\setminus\Omega(P^{\prime})|\ge \Big(\frac{1}{2}-\frac{1}{2^{n+3}}\Big)|P^{\prime}|\ge \frac{1}{4}|P^{\prime}|. \end{align} $$
For a.e.
![]() $y\in G_{P^{\prime }}\setminus \Omega (P^{\prime })\subset P^{\prime } \setminus \big (\Omega _{1}(P) \cup \Omega _{1}(P^{\prime })\big )$
we have
$y\in G_{P^{\prime }}\setminus \Omega (P^{\prime })\subset P^{\prime } \setminus \big (\Omega _{1}(P) \cup \Omega _{1}(P^{\prime })\big )$
we have
 $$ \begin{align*} \int_{P^{\prime}}|f_{P^{\prime},P}|^{r}g&\le 2^{r}\int_{P^{\prime}}|f_{P^{\prime},P}(x)-f_{P^{\prime},P}(y)|^{r}g(x)\,\mathrm{d} x+4^{r}(\alpha_{P^{\prime}}^{r}+\alpha_{P}^{r})\int_{P^{\prime}}g. \end{align*} $$
$$ \begin{align*} \int_{P^{\prime}}|f_{P^{\prime},P}|^{r}g&\le 2^{r}\int_{P^{\prime}}|f_{P^{\prime},P}(x)-f_{P^{\prime},P}(y)|^{r}g(x)\,\mathrm{d} x+4^{r}(\alpha_{P^{\prime}}^{r}+\alpha_{P}^{r})\int_{P^{\prime}}g. \end{align*} $$
Integrating over
![]() $G_{P^{\prime }}\setminus \Omega (P^{\prime })$
and using (3.7), we obtain
$G_{P^{\prime }}\setminus \Omega (P^{\prime })$
and using (3.7), we obtain
 $$ \begin{align*} \int_{P^{\prime}}|f_{P^{\prime},P}|^{r}g\le 4&\cdot2^{r}\frac{1}{|P^{\prime}|}\int_{P^{\prime}}\int_{P^{\prime}}|f_{P^{\prime},P}(x)-f_{P^{\prime},P}(y)|^{r}g(x)\,\mathrm{d} x\,\mathrm{d} y\\ &\quad +4^{r}(\alpha_{P^{\prime}}^{r}+\alpha_{P}^{r})\int_{P^{\prime}}g. \end{align*} $$
$$ \begin{align*} \int_{P^{\prime}}|f_{P^{\prime},P}|^{r}g\le 4&\cdot2^{r}\frac{1}{|P^{\prime}|}\int_{P^{\prime}}\int_{P^{\prime}}|f_{P^{\prime},P}(x)-f_{P^{\prime},P}(y)|^{r}g(x)\,\mathrm{d} x\,\mathrm{d} y\\ &\quad +4^{r}(\alpha_{P^{\prime}}^{r}+\alpha_{P}^{r})\int_{P^{\prime}}g. \end{align*} $$
By Hölder’s inequality,
 $$ \begin{align*} \frac{1}{|P^{\prime}|}\int_{P^{\prime}}\int_{P^{\prime}}|f_{P^{\prime},P}(x)-f_{P^{\prime},P}(y)|^{r}g(x)dxdy &\le\operatorname{\mathrm{osc}}_{q}(f_{P^{\prime},P};P^{\prime})^{r}\cdot \langle g\rangle_{(q/r)^{\prime},P^{\prime}}|P^{\prime}|\\ &\le \inf_{x^{\prime} \in P^{\prime}}(m_{P,q}^{\#}f)(x^{\prime})^{r}\langle g\rangle_{(q/r)^{\prime},P^{\prime}}|P^{\prime}|\\&\le \alpha_{P}^{r}\langle g\rangle_{(q/r)^{\prime},P^{\prime}}|P^{\prime}|, \end{align*} $$
$$ \begin{align*} \frac{1}{|P^{\prime}|}\int_{P^{\prime}}\int_{P^{\prime}}|f_{P^{\prime},P}(x)-f_{P^{\prime},P}(y)|^{r}g(x)dxdy &\le\operatorname{\mathrm{osc}}_{q}(f_{P^{\prime},P};P^{\prime})^{r}\cdot \langle g\rangle_{(q/r)^{\prime},P^{\prime}}|P^{\prime}|\\ &\le \inf_{x^{\prime} \in P^{\prime}}(m_{P,q}^{\#}f)(x^{\prime})^{r}\langle g\rangle_{(q/r)^{\prime},P^{\prime}}|P^{\prime}|\\&\le \alpha_{P}^{r}\langle g\rangle_{(q/r)^{\prime},P^{\prime}}|P^{\prime}|, \end{align*} $$
which, along with the previous estimate, implies
 $$ \begin{align} \int_{P^{\prime}}|f_{P^{\prime},P}|^{r}g\le 5\cdot 4^{r}\Big(\alpha_{P}^{r}\langle g\rangle_{(q/r)^{\prime},P^{\prime}}|P^{\prime}| + (\alpha_{P^{\prime}}^{r}+\alpha_{P}^{r})\int_{P^{\prime}}g\Big). \end{align} $$
$$ \begin{align} \int_{P^{\prime}}|f_{P^{\prime},P}|^{r}g\le 5\cdot 4^{r}\Big(\alpha_{P}^{r}\langle g\rangle_{(q/r)^{\prime},P^{\prime}}|P^{\prime}| + (\alpha_{P^{\prime}}^{r}+\alpha_{P}^{r})\int_{P^{\prime}}g\Big). \end{align} $$
Now note that, by Hölder’s inequality, we have
 $$ \begin{align*} \sum_{\substack{P^{\prime}\in {\mathcal F}_{k+1}:\\P^{\prime}\subset P}} \alpha_{P}^{r}\langle g\rangle_{(q/r)^{\prime},P^{\prime}}|P^{\prime}| &\leq \alpha_{P}^{r} \Big(\sum_{\substack{P^{\prime}\in {\mathcal F}_{k+1}:\\P^{\prime}\subset P}} \int_{P^{\prime}} g^{(q/r)^{\prime}}\Big)^{\frac{1}{(q/r)^{\prime}}} \cdot \Big(\sum_{\substack{P^{\prime}\in {\mathcal F}_{k+1}:\\P^{\prime}\subset P}}|P^{\prime}|\Big)^{\frac{r}{q}}\\ &\leq \alpha_{P}^{r} \langle g \rangle_{(q/r)^{\prime},P} \lvert P \rvert. \end{align*} $$
$$ \begin{align*} \sum_{\substack{P^{\prime}\in {\mathcal F}_{k+1}:\\P^{\prime}\subset P}} \alpha_{P}^{r}\langle g\rangle_{(q/r)^{\prime},P^{\prime}}|P^{\prime}| &\leq \alpha_{P}^{r} \Big(\sum_{\substack{P^{\prime}\in {\mathcal F}_{k+1}:\\P^{\prime}\subset P}} \int_{P^{\prime}} g^{(q/r)^{\prime}}\Big)^{\frac{1}{(q/r)^{\prime}}} \cdot \Big(\sum_{\substack{P^{\prime}\in {\mathcal F}_{k+1}:\\P^{\prime}\subset P}}|P^{\prime}|\Big)^{\frac{r}{q}}\\ &\leq \alpha_{P}^{r} \langle g \rangle_{(q/r)^{\prime},P} \lvert P \rvert. \end{align*} $$
Combining this estimate with (3.5), (3.6) and (3.8), we obtain
 $$ \begin{align*} \int_{Q}|f_{Q}|^{r}g&\le 6\cdot 4^{r}\cdot C_{r}\Big(\sum_{k=0}^{\infty}\sum_{P\in {\mathcal F}_{k}}\Big(\alpha_{P}^{r}\int_{P}g+\sum_{P^{\prime}\in {\mathcal F}_{k+1}:P^{\prime}\subset P}\alpha_{P^{\prime}}^{r}\int_{P^{\prime}}g\Big)+\sum_{k=0}^{\infty}\sum_{P\in {\mathcal F}_{k}}\alpha_{P}^{r}\langle g\rangle_{(q/r)^{\prime},P}|P|\Big)\\ &\le 18\cdot 4^{r} \cdot C_{r}\sum_{P\in {\mathcal F}}\alpha_{P}^{r}\langle g\rangle_{(q/r)^{\prime},P}|P|, \end{align*} $$
$$ \begin{align*} \int_{Q}|f_{Q}|^{r}g&\le 6\cdot 4^{r}\cdot C_{r}\Big(\sum_{k=0}^{\infty}\sum_{P\in {\mathcal F}_{k}}\Big(\alpha_{P}^{r}\int_{P}g+\sum_{P^{\prime}\in {\mathcal F}_{k+1}:P^{\prime}\subset P}\alpha_{P^{\prime}}^{r}\int_{P^{\prime}}g\Big)+\sum_{k=0}^{\infty}\sum_{P\in {\mathcal F}_{k}}\alpha_{P}^{r}\langle g\rangle_{(q/r)^{\prime},P}|P|\Big)\\ &\le 18\cdot 4^{r} \cdot C_{r}\sum_{P\in {\mathcal F}}\alpha_{P}^{r}\langle g\rangle_{(q/r)^{\prime},P}|P|, \end{align*} $$
which completes the proof.
3.4. Sparse domination in spaces of homogeneous type
A space of homogeneous type
![]() $(S,d,\mu )$
, originally introduced by Coifman and Weiss in [Reference Coifman and Weiss12], is a set S equipped with a quasi-metric d and a doubling Borel measure
$(S,d,\mu )$
, originally introduced by Coifman and Weiss in [Reference Coifman and Weiss12], is a set S equipped with a quasi-metric d and a doubling Borel measure
![]() $\mu $
. That is, a metric d which, instead of the triangle inequality, satisfies
$\mu $
. That is, a metric d which, instead of the triangle inequality, satisfies
for some
![]() $c_{d}\geq 1$
and a Borel measure
$c_{d}\geq 1$
and a Borel measure
![]() $\mu $
that satisfies the doubling ball property
$\mu $
that satisfies the doubling ball property
for some
![]() $c_{\mu }\geq 1$
.
$c_{\mu }\geq 1$
.
It was shown by Anderson and Vagharshakyan [Reference Anderson and Vagharshakyan1] that the sparse domination principle based on the median oscillation estimate (1.1) could be generalised from the Euclidean space
![]() $\mathbb {R}^{n}$
equipped with the Lebesgue measure to a space of homogeneous type. Later, in [Reference Lorist39], it was shown by the second author that the sparse domination principle for operators in [Reference Lerner34, Reference Lerner and Ombrosi37] also generalises directly to spaces of homogeneous type. Doing similar adaptations as in [Reference Lorist39], Theorems 3.2 and 3.4 also generalise to this setting.
$\mathbb {R}^{n}$
equipped with the Lebesgue measure to a space of homogeneous type. Later, in [Reference Lorist39], it was shown by the second author that the sparse domination principle for operators in [Reference Lerner34, Reference Lerner and Ombrosi37] also generalises directly to spaces of homogeneous type. Doing similar adaptations as in [Reference Lorist39], Theorems 3.2 and 3.4 also generalise to this setting.
4. Previous known results from our sparse domination principles
In this section we will show that Theorems 3.2 and 3.4 imply a number of the previously known results.
4.1. The local mean oscillation estimate
Let us start by showing that Theorem 3.2 implies (1.1) or, more generally, its vector-valued variant by Hänninen and Hytönen [Reference Hänninen and Hytönen18].
Let X be a Banach space and
![]() $f \colon \mathbb {R}^{n}\to X$
be a strongly measurable function. Given
$f \colon \mathbb {R}^{n}\to X$
be a strongly measurable function. Given
![]() $0<\lambda <1$
, the local mean oscillation of f on
$0<\lambda <1$
, the local mean oscillation of f on
![]() $Q \in \mathcal {Q}$
is defined by
$Q \in \mathcal {Q}$
is defined by
 $$ \begin{align*}\omega_{\lambda}(f;Q)=\inf_{c \in X} \big(\lVert f-c \rVert_{X}\chi_{Q}\big)^{*}\big(\lambda|Q|\big).\end{align*} $$
$$ \begin{align*}\omega_{\lambda}(f;Q)=\inf_{c \in X} \big(\lVert f-c \rVert_{X}\chi_{Q}\big)^{*}\big(\lambda|Q|\big).\end{align*} $$
Moreover, for
 $0<\lambda <\frac 12$
, we define the quasi-optimal center of oscillation
$0<\lambda <\frac 12$
, we define the quasi-optimal center of oscillation
![]() $c_{\lambda }(f;Q)$
as any vector
$c_{\lambda }(f;Q)$
as any vector
![]() $c \in X$
such that
$c \in X$
such that
 $$ \begin{align*} \big(\lVert f-c \rVert_{X}\chi_{Q}\big)^{*}\big(\lambda|Q|\big) \leq 2\, \omega_{\lambda}(f;Q); \end{align*} $$
$$ \begin{align*} \big(\lVert f-c \rVert_{X}\chi_{Q}\big)^{*}\big(\lambda|Q|\big) \leq 2\, \omega_{\lambda}(f;Q); \end{align*} $$
see [Reference Hänninen and Hytönen18, Section 4] for an introduction. We will use the following property of this object: for
 $0<\lambda \leq \kappa <\frac 12$
, we have for any quasi-optimal center of oscillation
$0<\lambda \leq \kappa <\frac 12$
, we have for any quasi-optimal center of oscillation
![]() $c_{\kappa }(f;Q)$
that
$c_{\kappa }(f;Q)$
that
 $$ \begin{align} \big(\lVert f-c_{\kappa}(f;Q) \rVert_{X}\chi_{Q}\big)^{*}\big(\lambda|Q|\big) \leq 4\, \omega_{\lambda}(f;Q); \end{align} $$
$$ \begin{align} \big(\lVert f-c_{\kappa}(f;Q) \rVert_{X}\chi_{Q}\big)^{*}\big(\lambda|Q|\big) \leq 4\, \omega_{\lambda}(f;Q); \end{align} $$
see [Reference Hänninen and Hytönen18, Lemma 4.10].
Theorem 4.1 [Reference Hänninen and Hytönen18]
Let X be a Banach space and let
![]() $f\colon \mathbb {R}^{n} \to X$
be strongly measurable. For every cube
$f\colon \mathbb {R}^{n} \to X$
be strongly measurable. For every cube
![]() $Q\in {\mathcal Q}$
and
$Q\in {\mathcal Q}$
and
![]() $\eta \in (0,1)$
, there exists an
$\eta \in (0,1)$
, there exists an
![]() $\eta $
-sparse family
$\eta $
-sparse family
![]() ${\mathcal F}\subset {\mathcal D}(Q)$
such that for any
${\mathcal F}\subset {\mathcal D}(Q)$
such that for any
![]() $c_{1/4}(f;Q)$
and for a.e.
$c_{1/4}(f;Q)$
and for a.e.
![]() $x\in Q$
,
$x\in Q$
,
 $$ \begin{align*} \lVert f(x)-c_{1/4}(f;Q) \rVert_{X}\lesssim \sum_{P\in {\mathcal F}}\omega_{\frac{1-\eta}{2^{n+2}}}(f;P)\chi_{P}(x). \end{align*} $$
$$ \begin{align*} \lVert f(x)-c_{1/4}(f;Q) \rVert_{X}\lesssim \sum_{P\in {\mathcal F}}\omega_{\frac{1-\eta}{2^{n+2}}}(f;P)\chi_{P}(x). \end{align*} $$
Proof. For
![]() $Q\in {\mathcal Q}$
and
$Q\in {\mathcal Q}$
and
![]() $P\in {\mathcal D}(Q)$
define
$P\in {\mathcal D}(Q)$
define
 $$ \begin{align*} f_{Q}&:=\lVert f-c_{1/4}(f;Q) \rVert_{X},\\ f_{P,Q}&:=\lVert c_{1/4}(f;P) - c_{1/4}(f;Q) \rVert, \end{align*} $$
$$ \begin{align*} f_{Q}&:=\lVert f-c_{1/4}(f;Q) \rVert_{X},\\ f_{P,Q}&:=\lVert c_{1/4}(f;P) - c_{1/4}(f;Q) \rVert, \end{align*} $$
where for any cube
![]() $Q \in \mathcal {Q}$
we fix a quasi-optimal center of oscillation
$Q \in \mathcal {Q}$
we fix a quasi-optimal center of oscillation
![]() $c_{1/4}(f;Q)$
.
$c_{1/4}(f;Q)$
.
The family
![]() $\{f_{Q}, f_{P,Q}\}_{Q \in \mathcal {Q},P \in \mathcal {D}(Q)}$
satisfies the
$\{f_{Q}, f_{P,Q}\}_{Q \in \mathcal {Q},P \in \mathcal {D}(Q)}$
satisfies the
![]() $\ell ^{1}$
-condition with
$\ell ^{1}$
-condition with
![]() ${C_{1}=1}$
by the triangle inequality and (3.1) holds as well. Therefore, by Theorem 3.2, there exists an
${C_{1}=1}$
by the triangle inequality and (3.1) holds as well. Therefore, by Theorem 3.2, there exists an
![]() $\eta $
-sparse family
$\eta $
-sparse family
![]() ${\mathcal F}\subset {\mathcal D}(Q)$
such that for a.e.
${\mathcal F}\subset {\mathcal D}(Q)$
such that for a.e.
![]() $x\in Q$
,
$x\in Q$
,
 $$ \begin{align*} \lVert f(x)-c_{1/4}(f;Q) \rVert_{X} \lesssim \sum_{P\in {\mathcal F}} \gamma_{P} \chi_{P}(x). \end{align*} $$
$$ \begin{align*} \lVert f(x)-c_{1/4}(f;Q) \rVert_{X} \lesssim \sum_{P\in {\mathcal F}} \gamma_{P} \chi_{P}(x). \end{align*} $$
The function
![]() $f_{P^{\prime },P}$
is a constant for every
$f_{P^{\prime },P}$
is a constant for every
![]() $P^{\prime }\in {\mathcal D}(P)$
and therefore
$P^{\prime }\in {\mathcal D}(P)$
and therefore
 $m^{\#}_{P}f=0$
. Hence, by (4.1),
$m^{\#}_{P}f=0$
. Hence, by (4.1),
 $$ \begin{align*} \gamma_{P}=\big(\lVert f-c_{1/4}(f;P) \rVert_{X}\chi_{P}\big)^{*}\big(|P|\tfrac{1-\eta}{2^{n+2}}\big)\le 4\omega_{\frac{1-\eta}{2^{n+2}}}(f;P), \end{align*} $$
$$ \begin{align*} \gamma_{P}=\big(\lVert f-c_{1/4}(f;P) \rVert_{X}\chi_{P}\big)^{*}\big(|P|\tfrac{1-\eta}{2^{n+2}}\big)\le 4\omega_{\frac{1-\eta}{2^{n+2}}}(f;P), \end{align*} $$
which completes the proof.
4.2. The
 $\ell ^{r}$
-sparse domination principle for operators
$\ell ^{r}$
-sparse domination principle for operators
Next we show that Theorem 3.2 implies the main result of the second author in [Reference Lorist39, Theorem 3.2] on pointwise
![]() $\ell ^{r}$
-sparse domination for a bounded operator
$\ell ^{r}$
-sparse domination for a bounded operator
![]() $T\colon L^{p} \to L^{p,\infty }$
. Moreover, due to our flexible setup, we also obtain the pointwise
$T\colon L^{p} \to L^{p,\infty }$
. Moreover, due to our flexible setup, we also obtain the pointwise
![]() $\ell ^{r}$
-sparse domination result for bounded operators
$\ell ^{r}$
-sparse domination result for bounded operators
![]() $T\colon L^{p} \to L^{q,\infty }$
in [Reference Lorist39, Theorem 3.4] without any additional effort.
$T\colon L^{p} \to L^{q,\infty }$
in [Reference Lorist39, Theorem 3.4] without any additional effort.
Let us first introduce some notation. Let
![]() ${\mathscr D}$
be a dyadic lattice and let
${\mathscr D}$
be a dyadic lattice and let
![]() $X,Y$
be Banach spaces,
$X,Y$
be Banach spaces,
![]() $p,q \in (0,\infty )$
and
$p,q \in (0,\infty )$
and
![]() $\alpha \ge 1$
. For a bounded operator
$\alpha \ge 1$
. For a bounded operator
we say that a family of operators
![]() $\{T_{Q}\}_{Q\in {\mathscr D}}$
from
$\{T_{Q}\}_{Q\in {\mathscr D}}$
from
![]() $L^{p}(\mathbb {R}^{n};X)$
to
$L^{p}(\mathbb {R}^{n};X)$
to
![]() $L^{q,\infty }(Q;Y)$
is an
$L^{q,\infty }(Q;Y)$
is an
![]() $\alpha $
-localisation family of T if for all
$\alpha $
-localisation family of T if for all
![]() $Q\in {\mathscr D}$
and
$Q\in {\mathscr D}$
and
![]() $f\in L^{p}(\mathbb {R}^{n};X)$
we have
$f\in L^{p}(\mathbb {R}^{n};X)$
we have
 $$ \begin{align*} T_{Q}(f\chi_{\alpha Q})(x)&=T_{Q}f(x), && x\in Q,\\ \|T_{Q}(f\chi_{\alpha Q})(x)\|_{Y}&\le \|T(f\chi_{\alpha Q})(x)\|_{Y},&&x\in Q. \end{align*} $$
$$ \begin{align*} T_{Q}(f\chi_{\alpha Q})(x)&=T_{Q}f(x), && x\in Q,\\ \|T_{Q}(f\chi_{\alpha Q})(x)\|_{Y}&\le \|T(f\chi_{\alpha Q})(x)\|_{Y},&&x\in Q. \end{align*} $$
The canonical example is, of course,
![]() $T_{Q}f:=T_{Q}(f\chi _{\alpha Q})$
for all
$T_{Q}f:=T_{Q}(f\chi _{\alpha Q})$
for all
![]() $Q \in \mathscr {D}$
.
$Q \in \mathscr {D}$
.
Using an
![]() $\alpha $
-localisation family of T, we can define operator variants of the
$\alpha $
-localisation family of T, we can define operator variants of the
![]() $\ell ^{r}$
-condition and the sharp maximal function
$\ell ^{r}$
-condition and the sharp maximal function
 $m_{Q}^{\#}f$
. Indeed, set
$m_{Q}^{\#}f$
. Indeed, set
![]() $T_{P,Q}:= T_{Q}-T_{P}$
and let
$T_{P,Q}:= T_{Q}-T_{P}$
and let
![]() $r \in (0,\infty )$
. We say that T satisfies a localised
$r \in (0,\infty )$
. We say that T satisfies a localised
![]() $\ell ^{r}$
-estimate if for every
$\ell ^{r}$
-estimate if for every
![]() $Q\in {\mathcal Q}$
and every
$Q\in {\mathcal Q}$
and every
![]() $P_{1},\dots , P_{m}\in {\mathcal D}(Q)$
with
$P_{1},\dots , P_{m}\in {\mathcal D}(Q)$
with
![]() $P_{m}\subset \dots \subset P_{1}$
and
$P_{m}\subset \dots \subset P_{1}$
and
![]() $f \in L^{p}(\mathbb {R}^{n};X)$
, we have for a.e.
$f \in L^{p}(\mathbb {R}^{n};X)$
, we have for a.e.
![]() $x \in P_{m}$
$x \in P_{m}$
 $$ \begin{align*}\|T_{P_{1}}f(x)\|_{Y}\le C_{r}\Big(\sum_{k=1}^{m-1}\|T_{P_{k+1},P_{k}}f(x)\|_{Y}^{r}+\|T_{P_{m}}f(x)\|_{Y}^{r}\Big)^{1/r}.\end{align*} $$
$$ \begin{align*}\|T_{P_{1}}f(x)\|_{Y}\le C_{r}\Big(\sum_{k=1}^{m-1}\|T_{P_{k+1},P_{k}}f(x)\|_{Y}^{r}+\|T_{P_{m}}f(x)\|_{Y}^{r}\Big)^{1/r}.\end{align*} $$
Observe that if
![]() $r \in (0,1]$
and
$r \in (0,1]$
and
![]() $T_{Q}f = T(f \chi _{\alpha Q})$
for some
$T_{Q}f = T(f \chi _{\alpha Q})$
for some
![]() $\alpha \geq 1$
, then this estimate holds trivially for every (sub)linear operator T with
$\alpha \geq 1$
, then this estimate holds trivially for every (sub)linear operator T with
![]() $C_{r}=1$
. If T satisfies a localised
$C_{r}=1$
. If T satisfies a localised
![]() $\ell ^{r}$
-estimate, then, setting
$\ell ^{r}$
-estimate, then, setting
for
![]() $Q \in \mathscr {D}$
and
$Q \in \mathscr {D}$
and
![]() $P \in \mathcal {D}(Q)$
, we obtain that the
$P \in \mathcal {D}(Q)$
, we obtain that the
![]() $\ell ^{r}$
-condition holds.
$\ell ^{r}$
-condition holds.
Next, the operator analogue of the sharp maximal function
 $m_{Q}^{\#}f$
for a cube
$m_{Q}^{\#}f$
for a cube
![]() $Q \in \mathcal {Q}$
is given by
$Q \in \mathcal {Q}$
is given by
 $$ \begin{align*}{\mathcal M}_{T,Q}^{\#}f(x)=\sup_{P\in {\mathcal D}(Q):x \in P}\operatorname*{\mbox{ess sup}}_{x^{\prime},x^{\prime\prime}\in P}\,\big\|T_{P,Q}f(x^{\prime})-T_{P,Q}f(x^{\prime\prime})\big\|_{Y},\qquad x \in \mathbb{R}^{n}.\end{align*} $$
$$ \begin{align*}{\mathcal M}_{T,Q}^{\#}f(x)=\sup_{P\in {\mathcal D}(Q):x \in P}\operatorname*{\mbox{ess sup}}_{x^{\prime},x^{\prime\prime}\in P}\,\big\|T_{P,Q}f(x^{\prime})-T_{P,Q}f(x^{\prime\prime})\big\|_{Y},\qquad x \in \mathbb{R}^{n}.\end{align*} $$
For
![]() $f_{P,Q}$
as in (4.3), we have
$f_{P,Q}$
as in (4.3), we have
and therefore
 $$ \begin{align} m_{Q}^{\#}f(x)\le {\mathcal M}_{T,Q}^{\#}f(x), \qquad x \in \mathbb{R}^{n}. \end{align} $$
$$ \begin{align} m_{Q}^{\#}f(x)\le {\mathcal M}_{T,Q}^{\#}f(x), \qquad x \in \mathbb{R}^{n}. \end{align} $$
We are now ready to prove the announced result from [Reference Lorist39], which in the diagonal case
![]() $p=q$
generalises the main result of [Reference Lerner and Ombrosi37].
$p=q$
generalises the main result of [Reference Lerner and Ombrosi37].
Theorem 4.2 [Reference Lorist39]
Let
![]() $\mathscr {D}$
be a dyadic lattice, let X and Y be Banach space, take
$\mathscr {D}$
be a dyadic lattice, let X and Y be Banach space, take
![]() $p,q,r \in (0,\infty )$
and let
$p,q,r \in (0,\infty )$
and let
![]() $\alpha \ge 1$
. Suppose that
$\alpha \ge 1$
. Suppose that
-
• T is a bounded operator from
 $L^{p}(\mathbb {R}^{n};X)$
to
$L^{p}(\mathbb {R}^{n};X)$
to
 $L^{q,\infty }(\mathbb {R}^{n};Y)$
with
$L^{q,\infty }(\mathbb {R}^{n};Y)$
with
 $\alpha $
-localisation family
$\alpha $
-localisation family
 $\{T_{Q}\}_{Q\in {\mathscr D}}$
.
$\{T_{Q}\}_{Q\in {\mathscr D}}$
. -
•
 ${\mathcal M}_{T,Q}^{\#}$
is bounded from
${\mathcal M}_{T,Q}^{\#}$
is bounded from
 $L^{p}(\mathbb {R}^{n};X)$
to
$L^{p}(\mathbb {R}^{n};X)$
to
 $L^{q,\infty }(\mathbb {R}^{n})$
uniformly in
$L^{q,\infty }(\mathbb {R}^{n})$
uniformly in
 ${Q\in {\mathscr D}}$
.
${Q\in {\mathscr D}}$
. -
• T satisfies a localised
 $\ell ^{r}$
-estimate.
$\ell ^{r}$
-estimate.
Then for any
![]() $f\in L^{p}(\mathbb {R}^{n};X)$
and
$f\in L^{p}(\mathbb {R}^{n};X)$
and
![]() $Q\in {\mathscr D}$
, there exists a
$Q\in {\mathscr D}$
, there exists a
![]() $\frac {1}{2}$
-sparse family
$\frac {1}{2}$
-sparse family
![]() ${\mathcal F}\subset {\mathcal D}(Q)$
such that for a.e.
${\mathcal F}\subset {\mathcal D}(Q)$
such that for a.e.
![]() $x \in Q$
,
$x \in Q$
,
 $$ \begin{align*}\|T_{Q}f(x)\|_{Y}\lesssim C_{T} \, C_{r}\, \Big(\sum_{P\in {\mathcal F}}\lvert \alpha P \rvert^{\frac{r}{p}-\frac{r}{q}}\langle \|f\|_{X} \rangle_{p, \alpha P}^{r}\chi_{P}(x)\Big)^{1/r},\end{align*} $$
$$ \begin{align*}\|T_{Q}f(x)\|_{Y}\lesssim C_{T} \, C_{r}\, \Big(\sum_{P\in {\mathcal F}}\lvert \alpha P \rvert^{\frac{r}{p}-\frac{r}{q}}\langle \|f\|_{X} \rangle_{p, \alpha P}^{r}\chi_{P}(x)\Big)^{1/r},\end{align*} $$
with
![]() $C_{T}:= \lVert T \rVert _{L^{p}\to L^{q,\infty }} + \sup _{Q \in \mathscr {D}} \lVert \mathcal {M}_{T,Q} \rVert _{L^{p}\to L^{q,\infty }}.$
$C_{T}:= \lVert T \rVert _{L^{p}\to L^{q,\infty }} + \sup _{Q \in \mathscr {D}} \lVert \mathcal {M}_{T,Q} \rVert _{L^{p}\to L^{q,\infty }}.$
Proof. The essence of the proof is already contained in the discussion preceding the theorem. Indeed, let
![]() $\{ f_{Q},f_{P,Q} \}_{Q \in \mathscr {D}, P \in \mathcal {D}(Q)}$
be as in (4.2) and (4.3), which satisfies the
$\{ f_{Q},f_{P,Q} \}_{Q \in \mathscr {D}, P \in \mathcal {D}(Q)}$
be as in (4.2) and (4.3), which satisfies the
![]() $\ell ^{r}$
-condition and also (3.1) holds. Hence, we are in position to apply Theorem 3.2 with
$\ell ^{r}$
-condition and also (3.1) holds. Hence, we are in position to apply Theorem 3.2 with
 $\eta =\frac {1}{2}$
(see also Remark 3.3). It remains to estimate
$\eta =\frac {1}{2}$
(see also Remark 3.3). It remains to estimate
![]() $\gamma _{P}$
provided by this theorem.
$\gamma _{P}$
provided by this theorem.
By the assumption on T we have
 $$ \begin{align*}(f_{P}\chi_{P})^{*}(|P|/2^{n+3})\lesssim \lVert T \rVert_{L^{p}\to L^{q,\infty}} \cdot \lvert \alpha P \rvert^{\frac{1}{p}-\frac{1}{q}} \langle\|f\|_{X}\rangle_{p, \alpha P}.\end{align*} $$
$$ \begin{align*}(f_{P}\chi_{P})^{*}(|P|/2^{n+3})\lesssim \lVert T \rVert_{L^{p}\to L^{q,\infty}} \cdot \lvert \alpha P \rvert^{\frac{1}{p}-\frac{1}{q}} \langle\|f\|_{X}\rangle_{p, \alpha P}.\end{align*} $$
Moreover, by the assumption on
 ${\mathcal M}_{T,P}^{\#}$
and (4.4), we have
${\mathcal M}_{T,P}^{\#}$
and (4.4), we have
 $$ \begin{align*}(m^{\#}_{P}\chi_{P})^{*}(|P|/2^{n+3})\lesssim \lVert \mathcal{M}_{T,Q} \rVert_{L^{p}\to L^{q,\infty}} \cdot \lvert \alpha P \rvert^{\frac{1}{p}-\frac{1}{q}}\langle\|f\|_{X}\rangle_{p, \alpha P},\end{align*} $$
$$ \begin{align*}(m^{\#}_{P}\chi_{P})^{*}(|P|/2^{n+3})\lesssim \lVert \mathcal{M}_{T,Q} \rVert_{L^{p}\to L^{q,\infty}} \cdot \lvert \alpha P \rvert^{\frac{1}{p}-\frac{1}{q}}\langle\|f\|_{X}\rangle_{p, \alpha P},\end{align*} $$
which completes the proof.
Remark 4.3. In [Reference Lorist39, Theorem 3.5] a sparse form domination principle was shown for operators. Analogous to the proof of Theorem 4.2, one can deduce [Reference Lorist39, Theorem 3.5] from our sparse form domination principle in Theorem 3.4.
Remark 4.4. Both papers [Reference Lerner and Ombrosi37] and [Reference Lorist39] contain a list of known sparse domination results for operators that fit our setting. For the reader’s convenience, we include a unified and extended list below.
-
• Calderón–Zygmund operators [Reference Lerner and Ombrosi37] with operator-valued kernel [Reference Lorist39].
-
• Maximally modulated Calderón–Zygmund operators [Reference Beltran3].
-
• Variational truncations of Calderón–Zygmund operators [Reference Ma, Torrea and Xu41, Reference Zorin-Kranich50].
-
• Multilinear singular integral operators with
 $L^{r}$
-Hörmander condition [Reference Li38].
$L^{r}$
-Hörmander condition [Reference Li38]. -
• Fractional integral operators with Hormänder kernel [Reference Ibañez-Firnkorn, Riveros and Vidal28].
-
• A class of pseudo-differential operators [Reference Beltran and Cladek4].
-
• The Rademacher [Reference Lorist39] and the lattice Hardy–Littlewood [Reference Hänninen and Lorist19] maximal operators.
-
• The intrinsic Littlewood–Paley square function [Reference Lorist40].
-
• Nonintegral operators falling outside the scope of Calderón–Zygmund theory [Reference Bernicot, Frey and Petermichl8] and the associated square functions [Reference Bailey, Brocchi and Reguera2].
-
• Rough homogeneous singular integrals [Reference Lerner35].
-
• The Marcinkiewicz integral with rough kernel [Reference Tao and Hu45].
Let us note that the boundedness of the corresponding sharp maximal operator is not explicitly contained in all of the above cited works and, in particular, sparse domination is obtained in a self-contained way in many of these citations. However, the presented arguments often imply the boundedness of the corresponding sharp maximal operator in our setting. For more details, we refer to [Reference Lerner and Ombrosi37, Section 5] and [Reference Lorist39, Section 9].
The three last items from the list fit the setting of bilinear form sparse domination expressed in Theorem 3.4.
5. Generalised Poincaré–Sobolev inequalities
As a first new application of our operator-free sparse domination principle, we will study generalised Poincaré–Sobolev inequalities as in [Reference Cejas, Mosquera, Pérez and Rela10, Reference Pérez and Rela44]. In particular, we will extend and improve [Reference Pérez and Rela44, Theorem 1.5 and 1.24] by Pérez and Rela.
Let us introduce some notation. Let
![]() $p,s \in [1,\infty )$
. For a functional
$p,s \in [1,\infty )$
. For a functional
![]() $a \colon \mathcal {Q} \to \mathbb {R}_{+}$
and a weight w, we say that a satisfies the
$a \colon \mathcal {Q} \to \mathbb {R}_{+}$
and a weight w, we say that a satisfies the
![]() $SD_{p}^{s}(w)$
-condition and write
$SD_{p}^{s}(w)$
-condition and write
![]() $a \in SD_{p}^{s}(w)$
, if for any cube
$a \in SD_{p}^{s}(w)$
, if for any cube
![]() $Q \in \mathcal {Q}$
and any family of pairwise disjoint
$Q \in \mathcal {Q}$
and any family of pairwise disjoint
![]() $\{ Q_{j} \} \subset \mathcal {D}(Q)$
we have
$\{ Q_{j} \} \subset \mathcal {D}(Q)$
we have
 $$ \begin{align*} \Big(\frac{1}{w(Q)}\sum_{j} a(Q_{j})^{p} w(Q_{j})\Big)^{1/p} \leq C\Big(\frac{\sum_{j}\lvert Q_{j} \rvert}{\lvert Q \rvert}\Big)^{{1/s}} a(Q). \end{align*} $$
$$ \begin{align*} \Big(\frac{1}{w(Q)}\sum_{j} a(Q_{j})^{p} w(Q_{j})\Big)^{1/p} \leq C\Big(\frac{\sum_{j}\lvert Q_{j} \rvert}{\lvert Q \rvert}\Big)^{{1/s}} a(Q). \end{align*} $$
The least admissible constant
![]() $C\geq 1$
is denoted by
$C\geq 1$
is denoted by
![]() $\lVert a \rVert _{SD_{p}^{s}(w)}$
. We note that the
$\lVert a \rVert _{SD_{p}^{s}(w)}$
. We note that the
![]() $SD_{p}^{s}(w)$
-condition can be thought of as an s-smallness preserving condition, and for examples of functionals
$SD_{p}^{s}(w)$
-condition can be thought of as an s-smallness preserving condition, and for examples of functionals
![]() $a \in SD_{p}^{s}(w)$
we refer to [Reference Pérez and Rela44].
$a \in SD_{p}^{s}(w)$
we refer to [Reference Pérez and Rela44].
Fix a cube
![]() $Q \in \mathcal {Q}$
and
$Q \in \mathcal {Q}$
and
 $f \in L^{1}_{\operatorname {\mathrm {loc}}}(\mathbb {R}^{n})$
. For
$f \in L^{1}_{\operatorname {\mathrm {loc}}}(\mathbb {R}^{n})$
. For
![]() $m \in \mathbb {N} \cup \{ 0 \}$
, we denote by
$m \in \mathbb {N} \cup \{ 0 \}$
, we denote by
![]() $P_{Q}f$
the projection of f onto the space of polynomials of degree at most m in n variables on Q. We refer to [Reference Pérez and Rela44, Section 8] for a proper introduction of this projection. Here we just note the following two properties that we will use of
$P_{Q}f$
the projection of f onto the space of polynomials of degree at most m in n variables on Q. We refer to [Reference Pérez and Rela44, Section 8] for a proper introduction of this projection. Here we just note the following two properties that we will use of
![]() $P_{Q}f$
:
$P_{Q}f$
:
-
• There is a
 $C_{m}>0$
such that (5.1)
$C_{m}>0$
such that (5.1) $$ \begin{align} \lVert P_{Q}f \rVert_{L^{\infty}(Q)} \leq C_{m} \frac{1}{\lvert Q \rvert} \int_{Q}\lvert f \rvert. \end{align} $$
$$ \begin{align} \lVert P_{Q}f \rVert_{L^{\infty}(Q)} \leq C_{m} \frac{1}{\lvert Q \rvert} \int_{Q}\lvert f \rvert. \end{align} $$
-
• For any polynomial
 $\pi $
of degree at most m in n variables, we have
$\pi $
of degree at most m in n variables, we have
 $P_{Q}(\pi ) = \pi $
on Q.
$P_{Q}(\pi ) = \pi $
on Q.
Furthermore, we note that when
![]() $m=0$
, we have
$m=0$
, we have
 $P_{Q}f =\frac {1}{|Q|}\int _{Q}f$
.
$P_{Q}f =\frac {1}{|Q|}\int _{Q}f$
.
In this language, the main result of Pérez and Rela reads as follows.
Theorem 5.1 [Reference Pérez and Rela44]
Let
![]() $p,s\in [1,\infty )$
and let
$p,s\in [1,\infty )$
and let
![]() $w\in A_{\infty }$
. Assume that
$w\in A_{\infty }$
. Assume that
![]() $a\in SD_{p}^{s}(w)$
. Let
$a\in SD_{p}^{s}(w)$
. Let
 $f\in L^{1}_{\operatorname {\mathrm {loc}}}({\mathbb R}^{n})$
be such that for all
$f\in L^{1}_{\operatorname {\mathrm {loc}}}({\mathbb R}^{n})$
be such that for all
![]() $Q \in \mathcal {Q}$
,
$Q \in \mathcal {Q}$
,
 $$ \begin{align*} \frac{1}{\lvert Q \rvert}\int_{Q} \lvert {f - P_{Q}f} \rvert \leq a(Q). \end{align*} $$
$$ \begin{align*} \frac{1}{\lvert Q \rvert}\int_{Q} \lvert {f - P_{Q}f} \rvert \leq a(Q). \end{align*} $$
Then, there is a constant
![]() $C_{n,m}>0$
such that for any
$C_{n,m}>0$
such that for any
![]() $Q \in \mathcal {Q}$
,
$Q \in \mathcal {Q}$
,
 $$ \begin{align} \Big(\frac{1}{w(Q)}\int_{Q} \lvert {f - P_{Q}f} \rvert^{p}w\Big)^{\frac1p} \leq C_{n,m}\, s \, \lVert a \rVert^{s}_{SD_{p}^{s}(w)} \, a(Q). \end{align} $$
$$ \begin{align} \Big(\frac{1}{w(Q)}\int_{Q} \lvert {f - P_{Q}f} \rvert^{p}w\Big)^{\frac1p} \leq C_{n,m}\, s \, \lVert a \rVert^{s}_{SD_{p}^{s}(w)} \, a(Q). \end{align} $$
Note that when
![]() $m \geq 1$
, the result of Pérez and Rela has an additional factor
$m \geq 1$
, the result of Pérez and Rela has an additional factor
![]() $2^{\frac {s+1}{p^{\prime }}}$
in the conclusion, but it was observed in [Reference Cejas, Mosquera, Pérez and Rela10, Theorem 2.1] that this factor can be omitted.
$2^{\frac {s+1}{p^{\prime }}}$
in the conclusion, but it was observed in [Reference Cejas, Mosquera, Pérez and Rela10, Theorem 2.1] that this factor can be omitted.
It was asked in [Reference Pérez and Rela44, Remark 1.6] whether the
![]() $A_{\infty }$
assumption in Theorem 5.1 can be removed. A partial result in this direction was provided by Martínez-Perales [Reference Martínez-Perales42].
$A_{\infty }$
assumption in Theorem 5.1 can be removed. A partial result in this direction was provided by Martínez-Perales [Reference Martínez-Perales42].
In order to state our main result, we will replace
![]() $L^{p}(w)$
-averages by arbitrary Banach function norms (see, e.g., [Reference Bennett and Sharpley7, Reference Zaanen49]). First we define a more general smallness preserving condition with respect to a Banach function norm. Note that the following condition with
$L^{p}(w)$
-averages by arbitrary Banach function norms (see, e.g., [Reference Bennett and Sharpley7, Reference Zaanen49]). First we define a more general smallness preserving condition with respect to a Banach function norm. Note that the following condition with
 $$ \begin{align} \begin{aligned} \lVert f \rVert_{X_{Q}} &:= \Big(\frac{1}{w(Q)}\int_{Q} \lvert f \rvert^{p}w\Big)^{1/p}, \qquad && Q \in \mathcal{Q},\\ \varphi(t) &:= \lVert a \rVert_{SD_{p}^{s}} \cdot t^{\frac{1}{s}}, && t \in [0,1], \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \lVert f \rVert_{X_{Q}} &:= \Big(\frac{1}{w(Q)}\int_{Q} \lvert f \rvert^{p}w\Big)^{1/p}, \qquad && Q \in \mathcal{Q},\\ \varphi(t) &:= \lVert a \rVert_{SD_{p}^{s}} \cdot t^{\frac{1}{s}}, && t \in [0,1], \end{aligned} \end{align} $$
coincides with the definition of the
![]() $SD_{p}^{s}(w)$
-condition.
$SD_{p}^{s}(w)$
-condition.
Definition 5.2. For
![]() $Q \in \mathcal {Q}$
let
$Q \in \mathcal {Q}$
let
![]() $\lVert \,\cdot \, \rVert _{X_{Q}}$
be a Banach function norm and let
$\lVert \,\cdot \, \rVert _{X_{Q}}$
be a Banach function norm and let
![]() $\varphi \colon [0,1] \to \mathbb {R}_{+}$
be increasing. For a functional
$\varphi \colon [0,1] \to \mathbb {R}_{+}$
be increasing. For a functional
![]() $a \colon \mathcal {Q} \to \mathbb {R}_{+}$
we say that a satisfies the
$a \colon \mathcal {Q} \to \mathbb {R}_{+}$
we say that a satisfies the
![]() $\varphi $
-smallness preserving condition if for any
$\varphi $
-smallness preserving condition if for any
![]() $Q \in \mathcal {Q}$
and any family of pairwise disjoint
$Q \in \mathcal {Q}$
and any family of pairwise disjoint
![]() $\{ Q_{j} \} \subset \mathcal {D}(Q)$
we have
$\{ Q_{j} \} \subset \mathcal {D}(Q)$
we have
 $$ \begin{align} \big\|\sum_{j}a(Q_{j})\chi_{Q_{j}}\big\|_{X_{Q}}\leq \varphi\Big(\frac{\sum_{j}\lvert Q_{j} \rvert}{\lvert Q \rvert}\Big)\cdot a(Q). \end{align} $$
$$ \begin{align} \big\|\sum_{j}a(Q_{j})\chi_{Q_{j}}\big\|_{X_{Q}}\leq \varphi\Big(\frac{\sum_{j}\lvert Q_{j} \rvert}{\lvert Q \rvert}\Big)\cdot a(Q). \end{align} $$
We are now ready to state the main result of this section.
Theorem 5.3. Fix
 $f \in L^{1}_{\operatorname {\mathrm {loc}}}(\mathbb {R}^{n})$
. For
$f \in L^{1}_{\operatorname {\mathrm {loc}}}(\mathbb {R}^{n})$
. For
![]() $Q \in \mathcal {Q}$
let
$Q \in \mathcal {Q}$
let
![]() $\lVert \,\cdot \, \rVert _{X_{Q}}$
be a Banach function norm and let
$\lVert \,\cdot \, \rVert _{X_{Q}}$
be a Banach function norm and let
![]() $a \colon \mathcal {Q} \to \mathbb {R}_{+}$
satisfy both the
$a \colon \mathcal {Q} \to \mathbb {R}_{+}$
satisfy both the
![]() $\varphi $
-smallness preserving condition and for all
$\varphi $
-smallness preserving condition and for all
![]() $Q \in \mathcal {Q}$
,
$Q \in \mathcal {Q}$
,
 $$ \begin{align*} \frac{1}{\lvert Q \rvert}\int_{Q} \lvert {f - P_{Q}f} \rvert \leq a(Q). \end{align*} $$
$$ \begin{align*} \frac{1}{\lvert Q \rvert}\int_{Q} \lvert {f - P_{Q}f} \rvert \leq a(Q). \end{align*} $$
Then there is a
![]() $C_{n,m}>0$
such that for all
$C_{n,m}>0$
such that for all
![]() $Q \in \mathcal {Q}$
,
$Q \in \mathcal {Q}$
,
 $$ \begin{align} \|(f-P_{Q}f)\chi_{Q}\|_{X_{Q}}\le C_{n,m} \,a(Q) \cdot \Big(\int_{0}^{1} \varphi(t) \tfrac{\mathrm{d} t}{t} +\varphi(1)\Big). \end{align} $$
$$ \begin{align} \|(f-P_{Q}f)\chi_{Q}\|_{X_{Q}}\le C_{n,m} \,a(Q) \cdot \Big(\int_{0}^{1} \varphi(t) \tfrac{\mathrm{d} t}{t} +\varphi(1)\Big). \end{align} $$
Taking
![]() $X_{Q}$
and
$X_{Q}$
and
![]() $\varphi $
as in (5.3), we have
$\varphi $
as in (5.3), we have
 $$ \begin{align*} \int_{0}^{1} \varphi(t) \tfrac{\mathrm{d} t}{t} +\varphi(1)= (s+1) \, \lVert a \rVert_{SD_{p}^{s}}. \end{align*} $$
$$ \begin{align*} \int_{0}^{1} \varphi(t) \tfrac{\mathrm{d} t}{t} +\varphi(1)= (s+1) \, \lVert a \rVert_{SD_{p}^{s}}. \end{align*} $$
Thus, we obtain an extension of Theorem 5.1 to arbitrary weights, which provides an affirmative answer to the question posed in [Reference Pérez and Rela44, Remark 1.6]. Moreover, we have a quantitative improvement over Theorem 5.1, even in the case
![]() $m=0$
and
$m=0$
and
![]() $s>1$
, since (5.5) holds with linear dependence on
$s>1$
, since (5.5) holds with linear dependence on
![]() $\lVert a \rVert _{SD_{p}^{s}(w)}$
, whereas one has
$\lVert a \rVert _{SD_{p}^{s}(w)}$
, whereas one has
 $\lVert a \rVert ^{s}_{SD_{p}^{s}(w)}$
in (5.2).
$\lVert a \rVert ^{s}_{SD_{p}^{s}(w)}$
in (5.2).
The key ingredient in our proof of Theorem 5.3 is the following sparse domination result in the spirit of Theorem 4.1.
Proposition 5.4. Let
 $f \in L^{1}_{\operatorname {\mathrm {loc}}}(\mathbb {R}^{n})$
. For any
$f \in L^{1}_{\operatorname {\mathrm {loc}}}(\mathbb {R}^{n})$
. For any
![]() $Q \in \mathcal {Q}$
and
$Q \in \mathcal {Q}$
and
![]() $\eta \in (0,1)$
there exists an
$\eta \in (0,1)$
there exists an
![]() $\eta $
-sparse family
$\eta $
-sparse family
![]() ${\mathcal F}\subset \mathcal {D}(Q)$
such that
${\mathcal F}\subset \mathcal {D}(Q)$
such that
 $$ \begin{align*} |f-P_{Q}f| \chi_{Q}\le C_{n,m}\frac{1}{1-\eta}\sum_{R\in {\mathcal F}}\left(\frac{1}{\lvert R \rvert}\int_{R}\lvert f - P_{R}f \rvert\right)\chi_{R}. \end{align*} $$
$$ \begin{align*} |f-P_{Q}f| \chi_{Q}\le C_{n,m}\frac{1}{1-\eta}\sum_{R\in {\mathcal F}}\left(\frac{1}{\lvert R \rvert}\int_{R}\lvert f - P_{R}f \rvert\right)\chi_{R}. \end{align*} $$
Proof. For
![]() $Q \in \mathcal {Q}$
and
$Q \in \mathcal {Q}$
and
![]() $R \in \mathcal {D}(Q)$
, define
$R \in \mathcal {D}(Q)$
, define
 $$ \begin{align*} f_{Q} &:= {{f - P_{Q}f}}\\ f_{R,Q} &:={{P_{R}f - P_{Q}f}}. \end{align*} $$
$$ \begin{align*} f_{Q} &:= {{f - P_{Q}f}}\\ f_{R,Q} &:={{P_{R}f - P_{Q}f}}. \end{align*} $$
The family
![]() $\{f_{Q},f_{R,Q}\}_{Q\in {\mathcal Q}, R\in {\mathcal D}(Q)}$
trivially satisfies the
$\{f_{Q},f_{R,Q}\}_{Q\in {\mathcal Q}, R\in {\mathcal D}(Q)}$
trivially satisfies the
![]() $\ell ^{1}$
-condition with
$\ell ^{1}$
-condition with
![]() $C_{r}=1$
and (3.1) holds.
$C_{r}=1$
and (3.1) holds.
For any
![]() $R^{\prime } \in \mathcal {D}(R)$
, we have by (5.1)
$R^{\prime } \in \mathcal {D}(R)$
, we have by (5.1)
 $$ \begin{align*} \lVert f_{R^{\prime},R} \rVert_{L^{\infty}(R^{\prime})} = \lVert P_{R^{\prime}}(f-P_{R}f) \rVert_{L^{\infty}(R^{\prime})} \leq C_{m} \, \frac{1}{\lvert R^{\prime} \rvert} \int_{R^{\prime}} \lvert f - P_{R}f \rvert, \end{align*} $$
$$ \begin{align*} \lVert f_{R^{\prime},R} \rVert_{L^{\infty}(R^{\prime})} = \lVert P_{R^{\prime}}(f-P_{R}f) \rVert_{L^{\infty}(R^{\prime})} \leq C_{m} \, \frac{1}{\lvert R^{\prime} \rvert} \int_{R^{\prime}} \lvert f - P_{R}f \rvert, \end{align*} $$
which implies
 $$ \begin{align*} m^{\#}_{R}f(x) \leq 2 C_{m}M \big((f-P_{R}f)\chi_{R}\big)(x), \qquad x \in \mathbb{R}^{n}. \end{align*} $$
$$ \begin{align*} m^{\#}_{R}f(x) \leq 2 C_{m}M \big((f-P_{R}f)\chi_{R}\big)(x), \qquad x \in \mathbb{R}^{n}. \end{align*} $$
Therefore, by Chebyshev’s inequality and the weak
![]() $L^{1}$
-boundedness of M, we have for any
$L^{1}$
-boundedness of M, we have for any
![]() $\eta \in (0,1)$
,
$\eta \in (0,1)$
,
 $$ \begin{align*} (f_{R}\chi_{R})^{*}\big(|R|\tfrac{1-\eta}{2^{n+2}}\big)+(m^{\#}_{R}f)^{*}\big(|R|\tfrac{1-\eta}{2^{n+2}}\big) \leq C_{n,m} \, \frac{1}{1-\eta}\cdot{\frac{1}{\lvert R \rvert} \int_{R} \lvert f - P_{R}f \rvert}, \end{align*} $$
$$ \begin{align*} (f_{R}\chi_{R})^{*}\big(|R|\tfrac{1-\eta}{2^{n+2}}\big)+(m^{\#}_{R}f)^{*}\big(|R|\tfrac{1-\eta}{2^{n+2}}\big) \leq C_{n,m} \, \frac{1}{1-\eta}\cdot{\frac{1}{\lvert R \rvert} \int_{R} \lvert f - P_{R}f \rvert}, \end{align*} $$
which, by Theorem 3.2, completes the proof.
Proof of Theorem 5.3
Fix a cube
![]() $Q\in {\mathcal Q}$
. By the main hypothesis of Theorem 5.3 combined with Proposition 5.4, there exists a
$Q\in {\mathcal Q}$
. By the main hypothesis of Theorem 5.3 combined with Proposition 5.4, there exists a
![]() $\frac 12$
-sparse family
$\frac 12$
-sparse family
![]() ${\mathcal F}\subset \mathcal {D}(Q)$
such that
${\mathcal F}\subset \mathcal {D}(Q)$
such that
 $$ \begin{align} |f-P_{Q}f|\le C_{n,m} \sum_{R\in {\mathcal F}}a(R)\chi_{R}. \end{align} $$
$$ \begin{align} |f-P_{Q}f|\le C_{n,m} \sum_{R\in {\mathcal F}}a(R)\chi_{R}. \end{align} $$
Write
![]() $\mathcal {F} = \bigcup _{k=0}^{\infty } \mathcal {F}_{k}$
, where
$\mathcal {F} = \bigcup _{k=0}^{\infty } \mathcal {F}_{k}$
, where
![]() $\mathcal {F}_{k}$
is as in the definition of a contracting family of dyadic cubes. Since
$\mathcal {F}_{k}$
is as in the definition of a contracting family of dyadic cubes. Since
![]() $\mathcal {F} $
is
$\mathcal {F} $
is
![]() $\frac 12$
-sparse, we have for any
$\frac 12$
-sparse, we have for any
![]() $k \in \mathbb {N}\cup \{ 0 \}$
,
$k \in \mathbb {N}\cup \{ 0 \}$
,
 $$ \begin{align*} \sum_{R \in \mathcal{F}_{k}} \lvert R \rvert \leq \frac1{2^{k}} \lvert Q \rvert, \end{align*} $$
$$ \begin{align*} \sum_{R \in \mathcal{F}_{k}} \lvert R \rvert \leq \frac1{2^{k}} \lvert Q \rvert, \end{align*} $$
which, along with the
![]() $\varphi $
-smallness preserving condition, implies
$\varphi $
-smallness preserving condition, implies
 $$ \begin{align*} \big\|\sum_{R \in \mathcal{F}}a(R)\chi_{R}\big\|_{X_{Q}}&\le \sum_{k=0}^{\infty} \big\|\sum_{R \in \mathcal{F}_{k}}a(R)\chi_{R}\big\|_{X_{Q}} \le a(Q) \,\sum_{k=0}^{\infty} \varphi(2^{-k}). \end{align*} $$
$$ \begin{align*} \big\|\sum_{R \in \mathcal{F}}a(R)\chi_{R}\big\|_{X_{Q}}&\le \sum_{k=0}^{\infty} \big\|\sum_{R \in \mathcal{F}_{k}}a(R)\chi_{R}\big\|_{X_{Q}} \le a(Q) \,\sum_{k=0}^{\infty} \varphi(2^{-k}). \end{align*} $$
Combined with (5.6), this implies
 $$ \begin{align*}\|(f-P_{Q}f)\chi_{Q}\|_{X_{Q}}\le C_{n,m} \, a(Q) \,\sum_{k=0}^{\infty} \varphi(2^{-k}).\end{align*} $$
$$ \begin{align*}\|(f-P_{Q}f)\chi_{Q}\|_{X_{Q}}\le C_{n,m} \, a(Q) \,\sum_{k=0}^{\infty} \varphi(2^{-k}).\end{align*} $$
The result now follows by noting
 $\sum _{k=1}^{\infty } \varphi (2^{-k}) \leq \int _{0}^{1} \varphi (t) \tfrac {\mathrm {d} t}{t}$
.
$\sum _{k=1}^{\infty } \varphi (2^{-k}) \leq \int _{0}^{1} \varphi (t) \tfrac {\mathrm {d} t}{t}$
.
Remark 5.5. Theorem 5.3 remains true for quasi-Banach function norms. In this case, one has to replace
 $\int _{0}^{1} \varphi (t) \tfrac {\mathrm {d} t}{t}$
by
$\int _{0}^{1} \varphi (t) \tfrac {\mathrm {d} t}{t}$
by
 $\big (\int _{0}^{1} \varphi (t)^{r} \tfrac {\mathrm {d} t}{t}\big )^{1/r}$
, where
$\big (\int _{0}^{1} \varphi (t)^{r} \tfrac {\mathrm {d} t}{t}\big )^{1/r}$
, where
![]() $r\in (0,1)$
is the exponent in the Aoki–Rolewicz theorem (see [Reference Kalton, Peck and Roberts29]).
$r\in (0,1)$
is the exponent in the Aoki–Rolewicz theorem (see [Reference Kalton, Peck and Roberts29]).
Remark 5.6. One can replace
![]() $\|(f-P_{Q}f)\chi _{Q}\|_{X_{Q}}$
in the left-hand side of the conclusion of Theorem 5.3 by
$\|(f-P_{Q}f)\chi _{Q}\|_{X_{Q}}$
in the left-hand side of the conclusion of Theorem 5.3 by
![]() $\|M_{Q}(f-P_{Q}f)\|_{X_{Q}}$
, where
$\|M_{Q}(f-P_{Q}f)\|_{X_{Q}}$
, where
![]() $M_{Q}$
is the local maximal operator given by
$M_{Q}$
is the local maximal operator given by
 $$ \begin{align*} M_{Q}f := \sup_{P \in \mathcal{D}(Q)} \langle f \rangle_{1,P} \chi_{P}. \end{align*} $$
$$ \begin{align*} M_{Q}f := \sup_{P \in \mathcal{D}(Q)} \langle f \rangle_{1,P} \chi_{P}. \end{align*} $$
Indeed, one can make a similar change in Proposition 5.4 by using
 $$ \begin{align*} f_{Q} &:= M_{Q}(f-P_{Q}f),\\ f_{R,Q} &:= f_{R}-f_{Q} \end{align*} $$
$$ \begin{align*} f_{Q} &:= M_{Q}(f-P_{Q}f),\\ f_{R,Q} &:= f_{R}-f_{Q} \end{align*} $$
in the proof. The usage of Chebyshev’s inequality is in this case replaced by the weak
![]() $L^{1}$
-boundedness of
$L^{1}$
-boundedness of
![]() $M_{Q}$
.
$M_{Q}$
.
Using Remark 5.6, one can recover, for example, the first main result of [Reference Canto and Pérez9]. For a weight w, a cube
![]() $Q \in \mathcal {Q}$
and
$Q \in \mathcal {Q}$
and
![]() $r>0$
, denote
$r>0$
, denote
 $$ \begin{align*} w_{r}(Q) := \lvert Q \rvert^{1/r^{\prime}} \Big(\int_{Q}w^{r}\Big)^{1/r}. \end{align*} $$
$$ \begin{align*} w_{r}(Q) := \lvert Q \rvert^{1/r^{\prime}} \Big(\int_{Q}w^{r}\Big)^{1/r}. \end{align*} $$
Furthermore, for
 $f \in L^{1}_{\operatorname {\mathrm {loc}}}(\mathbb {R}^{n})$
, define the polynomial sharp maximal function as
$f \in L^{1}_{\operatorname {\mathrm {loc}}}(\mathbb {R}^{n})$
, define the polynomial sharp maximal function as
 $$ \begin{align*} M^{\sharp}_{m}f(x):= \sup_{Q \ni x} \frac{1}{\lvert Q \rvert} \int_{Q}\lvert f-P_{Q}f \rvert. \end{align*} $$
$$ \begin{align*} M^{\sharp}_{m}f(x):= \sup_{Q \ni x} \frac{1}{\lvert Q \rvert} \int_{Q}\lvert f-P_{Q}f \rvert. \end{align*} $$
Corollary 5.7 [Reference Canto and Pérez9]
Let
 $f \in L^{1}_{\operatorname {\mathrm {loc}}}(\mathbb {R}^{n})$
, let w be a weight and take
$f \in L^{1}_{\operatorname {\mathrm {loc}}}(\mathbb {R}^{n})$
, let w be a weight and take
![]() $p \in [1,\infty )$
and
$p \in [1,\infty )$
and
![]() $r \in (1,\infty )$
. For any cube
$r \in (1,\infty )$
. For any cube
![]() $Q \in \mathcal {Q}$
we have
$Q \in \mathcal {Q}$
we have
 $$ \begin{align*} \Big(\frac{1}{w_{r}(Q)} \int_{Q} \Big(\frac{M_{Q}(f-P_{Q}f)}{M_{m}^{\sharp}f}\Big)^{p}w\Big)^{1/p} \leq C_{n,m}\, pr^{\prime}.\\[-16pt] \end{align*} $$
$$ \begin{align*} \Big(\frac{1}{w_{r}(Q)} \int_{Q} \Big(\frac{M_{Q}(f-P_{Q}f)}{M_{m}^{\sharp}f}\Big)^{p}w\Big)^{1/p} \leq C_{n,m}\, pr^{\prime}.\\[-16pt] \end{align*} $$
Proof. This follows directly from Theorem 5.3 combined with Remark 5.6 using the choices
 $$ \begin{align*} a(Q) &= \frac{1}{\lvert Q \rvert} \int_{Q}\lvert f-P_{Q}f \rvert,\\ \lVert g \rVert_{X_{Q}} &= \Big(\frac{1}{w_{r}(Q)} \int_{Q} \Big(\frac{\lvert g \rvert}{M_{m}^{\sharp}f}\Big)^{p}w\Big)^{1/p} \cdot a(Q).\\[-16pt] \end{align*} $$
$$ \begin{align*} a(Q) &= \frac{1}{\lvert Q \rvert} \int_{Q}\lvert f-P_{Q}f \rvert,\\ \lVert g \rVert_{X_{Q}} &= \Big(\frac{1}{w_{r}(Q)} \int_{Q} \Big(\frac{\lvert g \rvert}{M_{m}^{\sharp}f}\Big)^{p}w\Big)^{1/p} \cdot a(Q).\\[-16pt] \end{align*} $$
Indeed, for any
![]() $Q \in \mathcal {Q}$
and any family of pairwise disjoint
$Q \in \mathcal {Q}$
and any family of pairwise disjoint
![]() $\{ Q_{j} \} \subset \mathcal {D}(Q)$
, we have by Hölder’s inequality
$\{ Q_{j} \} \subset \mathcal {D}(Q)$
, we have by Hölder’s inequality
 $$ \begin{align*} \big\|\sum_{j}a(Q_{j})\chi_{Q_{j}}\big\|_{X_{Q}}&\leq \Big(\frac{1}{w_{r}(Q)} \sum_{j}\int_{Q_{j}} w \Big)^{1/p}\cdot a(Q) \\&\leq \Big(\frac{\sum_{j}\lvert Q_{j} \rvert}{\lvert Q \rvert}\Big)^{\frac{1}{pr^{\prime}}}\cdot a(Q),\\[-16pt] \end{align*} $$
$$ \begin{align*} \big\|\sum_{j}a(Q_{j})\chi_{Q_{j}}\big\|_{X_{Q}}&\leq \Big(\frac{1}{w_{r}(Q)} \sum_{j}\int_{Q_{j}} w \Big)^{1/p}\cdot a(Q) \\&\leq \Big(\frac{\sum_{j}\lvert Q_{j} \rvert}{\lvert Q \rvert}\Big)^{\frac{1}{pr^{\prime}}}\cdot a(Q),\\[-16pt] \end{align*} $$
so a satisfies the
![]() $\varphi $
-smallness preserving condition with
$\varphi $
-smallness preserving condition with
 $\varphi (t) = t^{\frac {1}{pr^{\prime }}}$
.
$\varphi (t) = t^{\frac {1}{pr^{\prime }}}$
.
6. Tent spaces
As our second new application, we will use our sparse domination principle to prove the main relation between two basic operators in the theory of tent spaces.
Let
![]() ${\mathbb R}^{n+1}_{+}=\{(y,t): y\in {\mathbb R}^{n}, t>0\}$
and, given
${\mathbb R}^{n+1}_{+}=\{(y,t): y\in {\mathbb R}^{n}, t>0\}$
and, given
![]() $\alpha>0$
, let
$\alpha>0$
, let
![]() $\Gamma _{\alpha }(x)$
denote the cone in
$\Gamma _{\alpha }(x)$
denote the cone in
![]() ${\mathbb R}^{n+1}_{+}$
with vertex in
${\mathbb R}^{n+1}_{+}$
with vertex in
![]() $x\in {\mathbb R}^{n}$
of aperture
$x\in {\mathbb R}^{n}$
of aperture
![]() $\alpha $
; that is,
$\alpha $
; that is,
Given a ball
![]() $B=B(x,r)$
in
$B=B(x,r)$
in
![]() ${\mathbb R}^{n}$
, denote the tent over B by
${\mathbb R}^{n}$
, denote the tent over B by
 $$ \begin{align*}\widehat B=\{(y,t)\in {\mathbb R}^{n+1}_{+}:|x-y|+t<r\}.\\[-16pt]\end{align*} $$
$$ \begin{align*}\widehat B=\{(y,t)\in {\mathbb R}^{n+1}_{+}:|x-y|+t<r\}.\\[-16pt]\end{align*} $$
For a measurable function
![]() $f\colon {\mathbb R}^{n+1}_{+} \to \mathbb {R}$
, define
$f\colon {\mathbb R}^{n+1}_{+} \to \mathbb {R}$
, define
 $$ \begin{align*} A^{(\alpha)}(f)(x)&:=\Big(\int_{\Gamma_{\alpha}(x)}|f(y,t)|^{2}\frac{\mathrm{d} y\mathrm{d} t}{t^{n+1}}\Big)^{1/2}, &&x \in \mathbb{R}^{n},\\ C(f)(x)&:=\sup_{B\ni x}\Big(\frac{1}{|B|}\int_{\widehat B}|f(y,t)|^{2}\frac{\mathrm{d} y\mathrm{d} t}{t}\Big)^{1/2}, &&x \in \mathbb{R}^{n},\\[-16pt] \end{align*} $$
$$ \begin{align*} A^{(\alpha)}(f)(x)&:=\Big(\int_{\Gamma_{\alpha}(x)}|f(y,t)|^{2}\frac{\mathrm{d} y\mathrm{d} t}{t^{n+1}}\Big)^{1/2}, &&x \in \mathbb{R}^{n},\\ C(f)(x)&:=\sup_{B\ni x}\Big(\frac{1}{|B|}\int_{\widehat B}|f(y,t)|^{2}\frac{\mathrm{d} y\mathrm{d} t}{t}\Big)^{1/2}, &&x \in \mathbb{R}^{n},\\[-16pt] \end{align*} $$
where the supremum is taken over all balls
![]() $B\subset \mathbb {R}^{n}$
containing x.
$B\subset \mathbb {R}^{n}$
containing x.
In [Reference Coifman, Meyer and Stein11], Coifman, Meyer and Stein defined the tent space
![]() $T^{p}_{\alpha }$
for
$T^{p}_{\alpha }$
for
![]() $p\in (0,\infty )$
and
$p\in (0,\infty )$
and
![]() $\alpha>0$
as the space of all measurable
$\alpha>0$
as the space of all measurable
![]() $f\colon {\mathbb R}^{n+1}_{+} \to \mathbb {R}$
such that
$f\colon {\mathbb R}^{n+1}_{+} \to \mathbb {R}$
such that
 $$ \begin{align*}\|f\|_{T^{p}_{\alpha}}:= \lVert A^{(\alpha)}(f) \rVert_{L^{p}(\mathbb{R}^{n})}<\infty.\\[-16pt]\end{align*} $$
$$ \begin{align*}\|f\|_{T^{p}_{\alpha}}:= \lVert A^{(\alpha)}(f) \rVert_{L^{p}(\mathbb{R}^{n})}<\infty.\\[-16pt]\end{align*} $$
It was shown in [Reference Coifman, Meyer and Stein11] that
 $T^{p}_{\alpha } = T^{p}_{\beta }$
for
$T^{p}_{\alpha } = T^{p}_{\beta }$
for
![]() $\alpha ,\beta>0$
, and thus it suffices to study
$\alpha ,\beta>0$
, and thus it suffices to study
 $T^{p}:=T^{p}_{1}$
. Furthermore, they deduced
$T^{p}:=T^{p}_{1}$
. Furthermore, they deduced
To prove these inequalities, it is useful to define a truncated version of
![]() $A^{(\alpha )}$
; that is, for
$A^{(\alpha )}$
; that is, for
![]() $h>0$
, set
$h>0$
, set
 $$ \begin{align*} A^{(\alpha)}_{h}(f)(x)&:=\Big(\int_{0}^{h}\int_{\lvert x-y \rvert<\alpha t}|f(y,t)|^{2}\frac{\mathrm{d} y\mathrm{d} t}{t^{n+1}}\Big)^{1/2}, &&x \in \mathbb{R}^{n}, \end{align*} $$
$$ \begin{align*} A^{(\alpha)}_{h}(f)(x)&:=\Big(\int_{0}^{h}\int_{\lvert x-y \rvert<\alpha t}|f(y,t)|^{2}\frac{\mathrm{d} y\mathrm{d} t}{t^{n+1}}\Big)^{1/2}, &&x \in \mathbb{R}^{n}, \end{align*} $$
and note that, using Fubini’s theorem, we can reformulate
![]() $C(f)(x)$
for
$C(f)(x)$
for
![]() $x \in \mathbb {R}^{n}$
as follows:
$x \in \mathbb {R}^{n}$
as follows:
 $$ \begin{align} \notag C(f)(x) &\eqsim \sup_{x \ni B} \Big(\frac{1}{\lvert B \rvert} \int_{0}^{r(B)} \int_{B} \lvert f(y,t) \rvert^{2} \frac{\lvert B(y,\alpha t) \rvert}{t^{n}} \frac{\mathrm{d} y \mathrm{d} t}{t}\Big)\\ &\eqsim \sup_{x \ni B} \Big(\frac{1}{\lvert B \rvert} \int_{B} \int_{0}^{r(B)} \int_{\lvert y-z \rvert \leq \alpha t}\lvert f(y,t) \rvert^{2} \frac{\mathrm{d} y \mathrm{d} t}{t^{n+1}}\,\mathrm{d} z\Big)^{1/2}\\ \notag&= \sup_{x \ni B} \Big(\frac{1}{\lvert B \rvert} \int_{B} A_{r(B)}^{(\alpha)}(f)(z)^{2} \,\mathrm{d} z\Big)^{1/2}, \end{align} $$
$$ \begin{align} \notag C(f)(x) &\eqsim \sup_{x \ni B} \Big(\frac{1}{\lvert B \rvert} \int_{0}^{r(B)} \int_{B} \lvert f(y,t) \rvert^{2} \frac{\lvert B(y,\alpha t) \rvert}{t^{n}} \frac{\mathrm{d} y \mathrm{d} t}{t}\Big)\\ &\eqsim \sup_{x \ni B} \Big(\frac{1}{\lvert B \rvert} \int_{B} \int_{0}^{r(B)} \int_{\lvert y-z \rvert \leq \alpha t}\lvert f(y,t) \rvert^{2} \frac{\mathrm{d} y \mathrm{d} t}{t^{n+1}}\,\mathrm{d} z\Big)^{1/2}\\ \notag&= \sup_{x \ni B} \Big(\frac{1}{\lvert B \rvert} \int_{B} A_{r(B)}^{(\alpha)}(f)(z)^{2} \,\mathrm{d} z\Big)^{1/2}, \end{align} $$
where
![]() $r(B)$
denotes the radius of the ball B and the implicit constants depend on
$r(B)$
denotes the radius of the ball B and the implicit constants depend on
![]() $\alpha>0$
.
$\alpha>0$
.
From (6.3) it is clear that
![]() $C(f)^{2} \lesssim M(A(f)^{2})$
, which directly implies (6.2) by the boundedness of the maximal operator. We will give a ‘sparse’ proof of the converse in (6.1).
$C(f)^{2} \lesssim M(A(f)^{2})$
, which directly implies (6.2) by the boundedness of the maximal operator. We will give a ‘sparse’ proof of the converse in (6.1).
Theorem 6.1. Take
![]() $\alpha>0$
and let
$\alpha>0$
and let
![]() $f \colon \mathbb {R}^{n+1}_{+} \to \mathbb {R}$
be measurable. For every cube
$f \colon \mathbb {R}^{n+1}_{+} \to \mathbb {R}$
be measurable. For every cube
![]() $Q\in \mathcal {Q}$
there exists a
$Q\in \mathcal {Q}$
there exists a
![]() $\frac {1}{2}$
-sparse family
$\frac {1}{2}$
-sparse family
![]() ${\mathcal F}\subset {\mathcal D}(Q)$
such that for a.e.
${\mathcal F}\subset {\mathcal D}(Q)$
such that for a.e.
![]() $x \in Q$
,
$x \in Q$
,
 $$ \begin{align*}A_{\ell_{Q}}^{(\alpha)}(f)(x)\lesssim \Big(\sum_{P\in {\mathcal F}} \frac{1}{\lvert P \rvert} \int_{P} A_{\ell_{P}}^{(4\alpha+\sqrt{n})}(f)^{2}\cdot \chi_{P}(x)\Big)^{1/2}.\end{align*} $$
$$ \begin{align*}A_{\ell_{Q}}^{(\alpha)}(f)(x)\lesssim \Big(\sum_{P\in {\mathcal F}} \frac{1}{\lvert P \rvert} \int_{P} A_{\ell_{P}}^{(4\alpha+\sqrt{n})}(f)^{2}\cdot \chi_{P}(x)\Big)^{1/2}.\end{align*} $$
Combining Theorem 6.1 with (6.3), we obtain for
![]() $\delta \in (0,2]$
and
$\delta \in (0,2]$
and
![]() $g \in L^{p^{\prime }}(\mathbb {R}^{n})$
,
$g \in L^{p^{\prime }}(\mathbb {R}^{n})$
,
 $$ \begin{align*} \int_{Q} A_{\ell_{Q}}^{(1)}(f)^{\delta}g&\lesssim \sum_{P\in {\mathcal F}}\Big(\frac{1}{|P|} \int_{P} A_{\ell_{P}}^{(4+\sqrt{n})}(f)^{2}\Big)^{\delta/2}\int_{P} g\\ &\lesssim \sum_{P\in {\mathcal F}}\int_{E_{P}}(C(f))^{\delta}\cdot Mg \\&\lesssim\|C(f)^{\delta}\|_{L^{p}(\mathbb{R}^{n})}\|g\|_{L^{p^{\prime}}(\mathbb{R}^{n})}. \end{align*} $$
$$ \begin{align*} \int_{Q} A_{\ell_{Q}}^{(1)}(f)^{\delta}g&\lesssim \sum_{P\in {\mathcal F}}\Big(\frac{1}{|P|} \int_{P} A_{\ell_{P}}^{(4+\sqrt{n})}(f)^{2}\Big)^{\delta/2}\int_{P} g\\ &\lesssim \sum_{P\in {\mathcal F}}\int_{E_{P}}(C(f))^{\delta}\cdot Mg \\&\lesssim\|C(f)^{\delta}\|_{L^{p}(\mathbb{R}^{n})}\|g\|_{L^{p^{\prime}}(\mathbb{R}^{n})}. \end{align*} $$
By duality and the monotone convergence theorem, this yields (6.1).
Proof of Theorem 6.1
Let
![]() $\Phi $
be a smooth function such that
$\Phi $
be a smooth function such that
![]() $\chi _{B(0,1)}\le \Phi \le \chi _{B(0,2)}$
and for
$\chi _{B(0,1)}\le \Phi \le \chi _{B(0,2)}$
and for
![]() $Q \in \mathcal {Q}$
define
$Q \in \mathcal {Q}$
define
 $$ \begin{align*} f_{Q}(x):= \Big(\int_{0}^{\ell_{Q}} \int_{\mathbb{R}^{n}} \lvert f(y,t) \rvert^{2} \cdot \Phi\big(\tfrac{x-y}{\alpha t}\big)^{2} \frac{\mathrm{d} y\mathrm{d} t}{t^{n+1}}\Big)^{1/2}, \qquad x \in Q. \end{align*} $$
$$ \begin{align*} f_{Q}(x):= \Big(\int_{0}^{\ell_{Q}} \int_{\mathbb{R}^{n}} \lvert f(y,t) \rvert^{2} \cdot \Phi\big(\tfrac{x-y}{\alpha t}\big)^{2} \frac{\mathrm{d} y\mathrm{d} t}{t^{n+1}}\Big)^{1/2}, \qquad x \in Q. \end{align*} $$
Observe that
 $A^{(\alpha )}_{\ell ^{Q}}(f) \leq f_{Q} \leq A^{(2\alpha )}_{\ell ^{Q}}(f)$
. For
$A^{(\alpha )}_{\ell ^{Q}}(f) \leq f_{Q} \leq A^{(2\alpha )}_{\ell ^{Q}}(f)$
. For
![]() $P \in \mathcal {D}(Q)$
, set
$P \in \mathcal {D}(Q)$
, set
 $$ \begin{align*} f_{P,Q}(x):= \Big(\int_{\ell_{P}}^{\ell_{Q}} \int_{\mathbb{R}^{n}} \lvert f(y,t) \rvert^{2} \cdot \Phi\big(\tfrac{x-y}{\alpha t}\big)^{2} \frac{\mathrm{d} y\mathrm{d} t}{t^{n+1}}\Big)^{1/2}, \qquad x \in P. \end{align*} $$
$$ \begin{align*} f_{P,Q}(x):= \Big(\int_{\ell_{P}}^{\ell_{Q}} \int_{\mathbb{R}^{n}} \lvert f(y,t) \rvert^{2} \cdot \Phi\big(\tfrac{x-y}{\alpha t}\big)^{2} \frac{\mathrm{d} y\mathrm{d} t}{t^{n+1}}\Big)^{1/2}, \qquad x \in P. \end{align*} $$
The family
![]() $\{f_{Q},f_{P,Q}\}_{Q \in \mathcal {Q}, P \in \mathcal {D}(Q)}$
trivially satisfies the
$\{f_{Q},f_{P,Q}\}_{Q \in \mathcal {Q}, P \in \mathcal {D}(Q)}$
trivially satisfies the
![]() $\ell ^{2}$
-condition with
$\ell ^{2}$
-condition with
![]() $C_{2}=1$
, and condition (3.1) holds as well. Therefore, by Theorem 3.2, there exists a
$C_{2}=1$
, and condition (3.1) holds as well. Therefore, by Theorem 3.2, there exists a
![]() $\frac {1}{2}$
-sparse family
$\frac {1}{2}$
-sparse family
![]() ${\mathcal F}\subset {\mathcal D}(Q)$
such that for a.e.
${\mathcal F}\subset {\mathcal D}(Q)$
such that for a.e.
![]() $x \in Q$
,
$x \in Q$
,
 $$ \begin{align} A^{(\alpha)}_{\ell_{Q}}(f)(x)\le f_{Q}(x)\lesssim \Big(\sum_{P\in {\mathcal F}}\gamma_{P}^{2}\chi_{P}(x)\Big)^{1/2}, \end{align} $$
$$ \begin{align} A^{(\alpha)}_{\ell_{Q}}(f)(x)\le f_{Q}(x)\lesssim \Big(\sum_{P\in {\mathcal F}}\gamma_{P}^{2}\chi_{P}(x)\Big)^{1/2}, \end{align} $$
where
 $$ \begin{align*}\gamma_{P}=(f_{P}\chi_{P})^{*}(|P|/2^{n+3})+(m^{\#}_{P}f)^{*}(|P|/2^{n+3}).\end{align*} $$
$$ \begin{align*}\gamma_{P}=(f_{P}\chi_{P})^{*}(|P|/2^{n+3})+(m^{\#}_{P}f)^{*}(|P|/2^{n+3}).\end{align*} $$
We start by analysing
 $m_{P}^{\#}f$
. Fix
$m_{P}^{\#}f$
. Fix
![]() $P \in \mathcal {F}$
and
$P \in \mathcal {F}$
and
![]() $x \in P$
. Let
$x \in P$
. Let
![]() $R\in {\mathcal D}(P)$
be such that
$R\in {\mathcal D}(P)$
be such that
![]() $x\in \mathbb {R}$
and take
$x\in \mathbb {R}$
and take
![]() $N \in \mathbb {N}$
such that
$N \in \mathbb {N}$
such that
![]() $2^{N}\ell _{R}=\ell _{P}$
. We have for
$2^{N}\ell _{R}=\ell _{P}$
. We have for
![]() $\xi ,\eta \in R$
,
$\xi ,\eta \in R$
,
 $$ \begin{align*} |f_{R,P}(\xi)-f_{R,P}(\eta)|& \leq \Big(\int_{\ell_{R}}^{\ell_{P}} \int_{\mathbb{R}^{n}} \lvert f(y,t) \rvert^{2}\cdot \big( \Phi\big(\tfrac{\xi-y}{\alpha t}\big)-\Phi\big(\tfrac{\eta-y}{\alpha t}\big)\big)^{2} \frac{\mathrm{d} y\mathrm{d} t}{t^{n+1}}\Big)^{1/2}\\ &\le\sum_{k=1}^{N}\Big(\int_{2^{k-1}\ell_{R}}^{2^{k}\ell_{R}} \int_{\mathbb{R}^{n}}\lvert f(y,t) \rvert^{2}\cdot \big( \Phi\big(\tfrac{\xi-y}{\alpha t}\big)-\Phi\big(\tfrac{\eta-y}{\alpha t}\big)\big)^{2} \frac{\mathrm{d} y\mathrm{d} t}{t^{n+1}}\Big)^{1/2}\\ &\lesssim \sum_{k=1}^{N} \frac{\lvert \xi-\eta \rvert}{ \alpha 2^{k} \ell_{R}}\Big(\int_{2^{k-1}\ell_{R}}^{2^{k}\ell_{R}} \int_{\lvert x-y \rvert \leq 4 \alpha t+\sqrt{n} \ell_{R}}\lvert f(y,t) \rvert^{2} \frac{\mathrm{d} y\mathrm{d} t}{t^{n+1}}\Big)^{1/2}\\ &\lesssim \sum_{k=1}^{N} \frac{1}{2^{k}}\Big(\int_{0}^{\ell_{P}} \int_{\lvert x-y \rvert<(4\alpha+\sqrt{n}) t}\lvert f(y,t) \rvert^{2} \frac{\mathrm{d} y\mathrm{d} t}{t^{n+1}}\Big)^{1/2}\\ &\leq A_{\ell_{P}}^{(4\alpha+\sqrt{n})}f(x). \end{align*} $$
$$ \begin{align*} |f_{R,P}(\xi)-f_{R,P}(\eta)|& \leq \Big(\int_{\ell_{R}}^{\ell_{P}} \int_{\mathbb{R}^{n}} \lvert f(y,t) \rvert^{2}\cdot \big( \Phi\big(\tfrac{\xi-y}{\alpha t}\big)-\Phi\big(\tfrac{\eta-y}{\alpha t}\big)\big)^{2} \frac{\mathrm{d} y\mathrm{d} t}{t^{n+1}}\Big)^{1/2}\\ &\le\sum_{k=1}^{N}\Big(\int_{2^{k-1}\ell_{R}}^{2^{k}\ell_{R}} \int_{\mathbb{R}^{n}}\lvert f(y,t) \rvert^{2}\cdot \big( \Phi\big(\tfrac{\xi-y}{\alpha t}\big)-\Phi\big(\tfrac{\eta-y}{\alpha t}\big)\big)^{2} \frac{\mathrm{d} y\mathrm{d} t}{t^{n+1}}\Big)^{1/2}\\ &\lesssim \sum_{k=1}^{N} \frac{\lvert \xi-\eta \rvert}{ \alpha 2^{k} \ell_{R}}\Big(\int_{2^{k-1}\ell_{R}}^{2^{k}\ell_{R}} \int_{\lvert x-y \rvert \leq 4 \alpha t+\sqrt{n} \ell_{R}}\lvert f(y,t) \rvert^{2} \frac{\mathrm{d} y\mathrm{d} t}{t^{n+1}}\Big)^{1/2}\\ &\lesssim \sum_{k=1}^{N} \frac{1}{2^{k}}\Big(\int_{0}^{\ell_{P}} \int_{\lvert x-y \rvert<(4\alpha+\sqrt{n}) t}\lvert f(y,t) \rvert^{2} \frac{\mathrm{d} y\mathrm{d} t}{t^{n+1}}\Big)^{1/2}\\ &\leq A_{\ell_{P}}^{(4\alpha+\sqrt{n})}f(x). \end{align*} $$
Therefore,
 $m_{P}^{\#}f(x) \lesssim A_{\ell _{P}}^{(4\alpha +\sqrt {n})}f(x)$
for
$m_{P}^{\#}f(x) \lesssim A_{\ell _{P}}^{(4\alpha +\sqrt {n})}f(x)$
for
![]() $x \in P$
. Since we already noted that
$x \in P$
. Since we already noted that
 $f_{P} \leq A^{(2\alpha )}_{\ell ^{P}}f$
, we obtain by (2.2),
$f_{P} \leq A^{(2\alpha )}_{\ell ^{P}}f$
, we obtain by (2.2),
 $$ \begin{align*} \gamma_{P} &\leq \Big(\frac{2^{n+3}}{\lvert P \rvert} \int_{P} f_{P}(z)^{2}\,\mathrm{d} z\Big)^{1/2}+\Big(\frac{2^{n+3}}{\lvert P \rvert} \int_{P} m_{P}^{\#}f(z)^{2}\,\mathrm{d} z\Big)^{1/2} \\&\lesssim \Big(\frac{1}{\lvert P \rvert} \int_{P} A_{\ell_{P}}^{(4\alpha+\sqrt{n})}(f)(z)^{2} \,\mathrm{d} z\Big)^{1/2}. \end{align*} $$
$$ \begin{align*} \gamma_{P} &\leq \Big(\frac{2^{n+3}}{\lvert P \rvert} \int_{P} f_{P}(z)^{2}\,\mathrm{d} z\Big)^{1/2}+\Big(\frac{2^{n+3}}{\lvert P \rvert} \int_{P} m_{P}^{\#}f(z)^{2}\,\mathrm{d} z\Big)^{1/2} \\&\lesssim \Big(\frac{1}{\lvert P \rvert} \int_{P} A_{\ell_{P}}^{(4\alpha+\sqrt{n})}(f)(z)^{2} \,\mathrm{d} z\Big)^{1/2}. \end{align*} $$
Combined with (6.4), this finishes the proof.
6.1. An improved good-
 $\lambda $
inequality
$\lambda $
inequality
The estimate (6.1) was shown in [Reference Coifman, Meyer and Stein11] using the equivalence of tent spaces with different apertures and the following good-
![]() $\lambda $
estimate: there exists a fixed
$\lambda $
estimate: there exists a fixed
![]() $\alpha>1$
and a constant
$\alpha>1$
and a constant
![]() $c>0$
so that for all
$c>0$
so that for all
![]() $\lambda>0$
and
$\lambda>0$
and
![]() $0<\gamma \le 1$
,
$0<\gamma \le 1$
,
 $$ \begin{align}\begin{aligned} \big|\{x\in \mathbb{R}^{n}:A(f)(x)>2\lambda, \,&C(f)(x)\le \gamma \lambda\}\big|\le c\,\gamma^{2} \big|\{x \in \mathbb{R}^{n}:A^{(\alpha)}(f)(x)>\lambda\}\big|, \end{aligned} \end{align} $$
$$ \begin{align}\begin{aligned} \big|\{x\in \mathbb{R}^{n}:A(f)(x)>2\lambda, \,&C(f)(x)\le \gamma \lambda\}\big|\le c\,\gamma^{2} \big|\{x \in \mathbb{R}^{n}:A^{(\alpha)}(f)(x)>\lambda\}\big|, \end{aligned} \end{align} $$
where we abbreviated
![]() $A(f):=A^{(1)}(f)$
. Using Theorem 6.1, we can show that the quadratic dependence on
$A(f):=A^{(1)}(f)$
. Using Theorem 6.1, we can show that the quadratic dependence on
![]() $\gamma $
in (6.5) can be improved to quadratic exponential dependence.
$\gamma $
in (6.5) can be improved to quadratic exponential dependence.
Theorem 6.2. Let
![]() $f \colon \mathbb {R}^{n+1}_{+} \to \mathbb {R}$
be measurable. There exist constants
$f \colon \mathbb {R}^{n+1}_{+} \to \mathbb {R}$
be measurable. There exist constants
![]() $\alpha>1$
and
$\alpha>1$
and
![]() $c>0$
so that for all
$c>0$
so that for all
![]() $\lambda>0$
and
$\lambda>0$
and
![]() $0<\gamma \le 1$
,
$0<\gamma \le 1$
,
 $$ \begin{align*} \big|\{x\in \mathbb{R}^{n}:A(f)(x)>2\lambda,\,& C(f)(x)\le \gamma \lambda\}\big|\le 2e^{-c/\gamma^{2}}\big|\{x\in \mathbb{R}^{n}:A^{(\alpha)}f(x)>\lambda\}\big|. \end{align*} $$
$$ \begin{align*} \big|\{x\in \mathbb{R}^{n}:A(f)(x)>2\lambda,\,& C(f)(x)\le \gamma \lambda\}\big|\le 2e^{-c/\gamma^{2}}\big|\{x\in \mathbb{R}^{n}:A^{(\alpha)}f(x)>\lambda\}\big|. \end{align*} $$
Before proving this lemma, we establish the following simple proposition.
Proposition 6.3. Let
![]() $Q \in \mathcal {Q}$
and let
$Q \in \mathcal {Q}$
and let
![]() ${\mathcal F}\subset {\mathcal D}(Q)$
be an
${\mathcal F}\subset {\mathcal D}(Q)$
be an
![]() $\eta $
-sparse family. Then we have for any
$\eta $
-sparse family. Then we have for any
![]() $\alpha>0$
$\alpha>0$
 $$ \begin{align*}\big|\big\{x\in Q:\sum_{P\in {\mathcal F}}\chi_{P}(x)>\alpha\big\}\big|\le \frac{1}{1-\eta}e^{-(\log\frac{1}{1-\eta})\alpha}|Q|.\end{align*} $$
$$ \begin{align*}\big|\big\{x\in Q:\sum_{P\in {\mathcal F}}\chi_{P}(x)>\alpha\big\}\big|\le \frac{1}{1-\eta}e^{-(\log\frac{1}{1-\eta})\alpha}|Q|.\end{align*} $$
Proof. Write
![]() ${\mathcal F}=\cup _{k=0}^{\infty }{\mathcal F}_{k}$
as in the definition of a contracting family of cubes. By
${\mathcal F}=\cup _{k=0}^{\infty }{\mathcal F}_{k}$
as in the definition of a contracting family of cubes. By
![]() $\eta $
-sparseness, we have
$\eta $
-sparseness, we have
![]() $|\Omega _{k}|\le (1-\eta )^{k}|Q|$
. Thus, it follows that
$|\Omega _{k}|\le (1-\eta )^{k}|Q|$
. Thus, it follows that
 $$ \begin{align*} \big|\big\{x\in Q:\sum_{P\in {\mathcal F}}\chi_{P}(x)>\alpha\big\}\big|&=\sum_{k=1}^{\infty}\lvert \Omega_{k-1} \rvert\chi_{(k-1,k]}(\alpha)\\ &\le |Q|\sum_{k=1}^{\infty}(1-\eta)^{k-1}\chi_{(k-1,k]}(\alpha)\le (1-\eta)^{\alpha-1}|Q|, \end{align*} $$
$$ \begin{align*} \big|\big\{x\in Q:\sum_{P\in {\mathcal F}}\chi_{P}(x)>\alpha\big\}\big|&=\sum_{k=1}^{\infty}\lvert \Omega_{k-1} \rvert\chi_{(k-1,k]}(\alpha)\\ &\le |Q|\sum_{k=1}^{\infty}(1-\eta)^{k-1}\chi_{(k-1,k]}(\alpha)\le (1-\eta)^{\alpha-1}|Q|, \end{align*} $$
which completes the proof.
Proof of Theorem 6.2
As in [Reference Coifman, Meyer and Stein11], we consider a Whitney decomposition
![]() $\{ Q_{j} \}_{j}$
of the open set
$\{ Q_{j} \}_{j}$
of the open set
where
![]() $\alpha>1$
will be chosen later on. Then it suffices to prove that for every
$\alpha>1$
will be chosen later on. Then it suffices to prove that for every
![]() $Q_{j}$
,
$Q_{j}$
,
 $$ \begin{align} \big|\{x\in Q_{j}:A(f)(x)>2\lambda, \,Cf(x)\le \gamma \lambda\}\big|\le c_{1}e^{-c_{2}/\gamma^{2}}|Q_{j}|. \end{align} $$
$$ \begin{align} \big|\{x\in Q_{j}:A(f)(x)>2\lambda, \,Cf(x)\le \gamma \lambda\}\big|\le c_{1}e^{-c_{2}/\gamma^{2}}|Q_{j}|. \end{align} $$
Define
 $f_{{Q_{j}}}(y,t):= f(y,t) \chi _{(\ell _{Q_{j}},\infty )}(t)$
and note that
$f_{{Q_{j}}}(y,t):= f(y,t) \chi _{(\ell _{Q_{j}},\infty )}(t)$
and note that
 $$ \begin{align*}A(f)\le A(f_{Q_{j}})+A_{\ell_{Q_{j}}}(f).\end{align*} $$
$$ \begin{align*}A(f)\le A(f_{Q_{j}})+A_{\ell_{Q_{j}}}(f).\end{align*} $$
Consider
![]() $A(f_{Q_{j}})(x)$
for
$A(f_{Q_{j}})(x)$
for
![]() $x\in Q_{j}$
. By the properties of the Whitney cubes, there exist
$x\in Q_{j}$
. By the properties of the Whitney cubes, there exist
![]() $z\in Q_{j}$
and
$z\in Q_{j}$
and
![]() $x_{j}\in \mathbb {R}^{n}$
such that
$x_{j}\in \mathbb {R}^{n}$
such that
![]() $|z-x_{j}|\le 4\sqrt {n}\ell _{Q_{j}}$
and
$|z-x_{j}|\le 4\sqrt {n}\ell _{Q_{j}}$
and
 $A^{(\alpha )}(f)(x_{j})\le \lambda $
. Hence, for
$A^{(\alpha )}(f)(x_{j})\le \lambda $
. Hence, for
![]() $(y,t) \in \mathbb {R}^{n+1}_{+}$
with
$(y,t) \in \mathbb {R}^{n+1}_{+}$
with
![]() $|y-x|<t$
and
$|y-x|<t$
and
![]() $t\ge \ell _{Q_{j}}$
, we obtain
$t\ge \ell _{Q_{j}}$
, we obtain
 $$ \begin{align*} |y-x_{j}|\le |y-x|+|x-z|+|z-x_{j}| <t+5\sqrt{n}\ell_{Q_{j}} \le (5\sqrt{n}+1)t. \end{align*} $$
$$ \begin{align*} |y-x_{j}|\le |y-x|+|x-z|+|z-x_{j}| <t+5\sqrt{n}\ell_{Q_{j}} \le (5\sqrt{n}+1)t. \end{align*} $$
Therefore, if
![]() $\alpha =5\sqrt {n}+1$
, then
$\alpha =5\sqrt {n}+1$
, then
 $A(f_{Q_{j}})(x)\le A^{(\alpha )}(f)(x_{j})\le \lambda $
for all
$A(f_{Q_{j}})(x)\le A^{(\alpha )}(f)(x_{j})\le \lambda $
for all
![]() $x\in Q_{j}$
. It follows that the left-hand side of (6.6) is bounded by
$x\in Q_{j}$
. It follows that the left-hand side of (6.6) is bounded by
 $$ \begin{align} \big|\{x\in Q_{j}:A_{\ell_{Q_{j}}}(f)(x)>\lambda,\, C(f)(x)\le \gamma \lambda\}\big|. \end{align} $$
$$ \begin{align} \big|\{x\in Q_{j}:A_{\ell_{Q_{j}}}(f)(x)>\lambda,\, C(f)(x)\le \gamma \lambda\}\big|. \end{align} $$
By Theorem 6.1 and (6.3), there exists a
![]() $\frac {1}{2}$
-sparse family
$\frac {1}{2}$
-sparse family
![]() ${\mathcal F}_{j}\subset {\mathcal D}(Q_{j})$
such that
${\mathcal F}_{j}\subset {\mathcal D}(Q_{j})$
such that
 $$ \begin{align*}A_{\ell_{Q_{j}}}(f)(x)^{2}\lesssim C(f)(x)^{2}\sum_{P\in {\mathcal F}_{j}}\chi_{P}(x), \qquad x \in Q_{j}.\end{align*} $$
$$ \begin{align*}A_{\ell_{Q_{j}}}(f)(x)^{2}\lesssim C(f)(x)^{2}\sum_{P\in {\mathcal F}_{j}}\chi_{P}(x), \qquad x \in Q_{j}.\end{align*} $$
Combined with Proposition 6.3, this implies that the expression in (6.7) is at most
 $$ \begin{align*} \big|\{x\in Q_{j}:\sum_{P\in {\mathcal F}_{j}}\chi_{P}(x)\gtrsim 1/\gamma^{2}\}\big|\le 2e^{-c/\gamma^{2}}|Q_{j}|, \end{align*} $$
$$ \begin{align*} \big|\{x\in Q_{j}:\sum_{P\in {\mathcal F}_{j}}\chi_{P}(x)\gtrsim 1/\gamma^{2}\}\big|\le 2e^{-c/\gamma^{2}}|Q_{j}|, \end{align*} $$
which completes the proof of (6.6) and therefore of the theorem.
6.2. Vector-valued tent spaces
Reinterpreting and extending the formulation of tent spaces by Harboure, Torrea and Viviani in [Reference Harboure, Torrea and Viviani20], Hytönen, van Neerven and Portal [Reference Hytönen, van Neerven and Portal24] extended tent spaces to the the vector-valued setting. In this subsection we will point out how the arguments of the preceding subsection extend to this setting.
In order to give the definition of these vector-valued tent spaces, we first need to introduce some notation. For a Banach space X and a Hilbert space H, denote the space of
![]() $\gamma $
-radonifying operators by
$\gamma $
-radonifying operators by
![]() $\gamma (H,X)\subseteq \mathcal {L}(X,H)$
. For an introduction to these spaces, we refer to [Reference Hytönen, van Neerven, Veraar and Weis26, Chapter 9].
$\gamma (H,X)\subseteq \mathcal {L}(X,H)$
. For an introduction to these spaces, we refer to [Reference Hytönen, van Neerven, Veraar and Weis26, Chapter 9].
For the remainder of this section, set
 $H:= L^{2}(\mathbb {R}^{n+1}_{+},\frac {\mathrm {d} y\mathrm {d} t}{t^{n+1}})$
. Then the space
$H:= L^{2}(\mathbb {R}^{n+1}_{+},\frac {\mathrm {d} y\mathrm {d} t}{t^{n+1}})$
. Then the space
![]() $\gamma (H,X)$
can be thought of as a square function space, since
$\gamma (H,X)$
can be thought of as a square function space, since
 $$ \begin{align*} \gamma(H,L^{p}(\mathbb{R}^{d})) = L^{p}(\mathbb{R}^{d};L^{2}(\mathbb{R}^{n+1}_{+},\tfrac{\mathrm{d} y\mathrm{d} t}{t^{n+1}})), \qquad p \in [1,\infty). \end{align*} $$
$$ \begin{align*} \gamma(H,L^{p}(\mathbb{R}^{d})) = L^{p}(\mathbb{R}^{d};L^{2}(\mathbb{R}^{n+1}_{+},\tfrac{\mathrm{d} y\mathrm{d} t}{t^{n+1}})), \qquad p \in [1,\infty). \end{align*} $$
Let
![]() $f \colon \mathbb {R}^{n+1}_{+} \to X$
be strongly measurable. If
$f \colon \mathbb {R}^{n+1}_{+} \to X$
be strongly measurable. If
![]() $\langle f,x^{*} \rangle \in H$
for all
$\langle f,x^{*} \rangle \in H$
for all
![]() $x^{*} \in X^{*}$
, we can define the operator
$x^{*} \in X^{*}$
, we can define the operator
![]() $I_{f} \in \mathcal {L}(H,X)$
by
$I_{f} \in \mathcal {L}(H,X)$
by
 $$ \begin{align*} I_{f}\varphi := \int_{\mathbb{R}^{n+1}_{+}} f(y,t) \varphi(y,t) \frac{\mathrm{d} y \mathrm{d} t}{t^{n+1}}, \qquad \varphi \in H, \end{align*} $$
$$ \begin{align*} I_{f}\varphi := \int_{\mathbb{R}^{n+1}_{+}} f(y,t) \varphi(y,t) \frac{\mathrm{d} y \mathrm{d} t}{t^{n+1}}, \qquad \varphi \in H, \end{align*} $$
where the integral is interpreted in the Pettis sense (see [Reference Hytönen, van Neerven, Veraar and Weis25, Theorem 1.2.37]). If
![]() $I_{f} \in \gamma (H,X)$
, we write with slight abuse of notation
$I_{f} \in \gamma (H,X)$
, we write with slight abuse of notation
![]() $f \in \gamma (H,X)$
and
$f \in \gamma (H,X)$
and
![]() $\lVert f \rVert _{\gamma (H,X)}:= \lVert I_{f} \rVert _{\gamma (H,X)}$
. Moreover, if
$\lVert f \rVert _{\gamma (H,X)}:= \lVert I_{f} \rVert _{\gamma (H,X)}$
. Moreover, if
![]() $I_{f} \notin \gamma (H,X)$
or
$I_{f} \notin \gamma (H,X)$
or
![]() $\langle f,x^{*} \rangle \notin H$
for some
$\langle f,x^{*} \rangle \notin H$
for some
![]() $x^{*} \in X^{*}$
, we set
$x^{*} \in X^{*}$
, we set
![]() $\lVert f \rVert _{\gamma (H,X)} = \infty $
.
$\lVert f \rVert _{\gamma (H,X)} = \infty $
.
We are now ready to define the vector-valued tent spaces introduced in [Reference Hytönen, van Neerven and Portal24]. For
![]() $\alpha>0$
and a strongly measurable
$\alpha>0$
and a strongly measurable
![]() $f \colon \mathbb {R}^{n+1}_{+} \to X$
, define
$f \colon \mathbb {R}^{n+1}_{+} \to X$
, define
 $$ \begin{align*} A^{(\alpha)}(f)(x)&:= \lVert f\cdot \chi_{\Gamma_{\alpha}(x)} \rVert_{\gamma(H,X)}, && x \in \mathbb{R}^{n}\\ A^{(\alpha)}_{h}(f)(x)&:= \lVert f\cdot \chi_{\Gamma_{\alpha}(x)} \cdot \chi_{\mathbb{R}^{n} \times (0,h)} \rVert_{\gamma(H,X)}, &&x \in \mathbb{R}^{n}, \, h>0. \end{align*} $$
$$ \begin{align*} A^{(\alpha)}(f)(x)&:= \lVert f\cdot \chi_{\Gamma_{\alpha}(x)} \rVert_{\gamma(H,X)}, && x \in \mathbb{R}^{n}\\ A^{(\alpha)}_{h}(f)(x)&:= \lVert f\cdot \chi_{\Gamma_{\alpha}(x)} \cdot \chi_{\mathbb{R}^{n} \times (0,h)} \rVert_{\gamma(H,X)}, &&x \in \mathbb{R}^{n}, \, h>0. \end{align*} $$
Since
![]() $\gamma (H,\mathbb {R})=H$
, this definition coincides with the scalar-valued definitions of
$\gamma (H,\mathbb {R})=H$
, this definition coincides with the scalar-valued definitions of
![]() $A^{(\alpha )}$
and
$A^{(\alpha )}$
and
 $A^{(\alpha )}_{h}$
. Therefore, it makes sense to define
$A^{(\alpha )}_{h}$
. Therefore, it makes sense to define
![]() $T^{p}_{\alpha }(X)$
as the completion of the space of all strongly measurable
$T^{p}_{\alpha }(X)$
as the completion of the space of all strongly measurable
![]() $f \colon \mathbb {R}^{n+1}_{+} \to X$
such that
$f \colon \mathbb {R}^{n+1}_{+} \to X$
such that
 $$ \begin{align*} \lVert f \rVert_{T_{\alpha}^{p}(X)} := \lVert A^{(\alpha)}(f) \rVert_{L^{p}(\mathbb{R}^{n})} <\infty. \end{align*} $$
$$ \begin{align*} \lVert f \rVert_{T_{\alpha}^{p}(X)} := \lVert A^{(\alpha)}(f) \rVert_{L^{p}(\mathbb{R}^{n})} <\infty. \end{align*} $$
It was shown in [Reference Hytönen, van Neerven and Portal24, Theorem 4.3] that, as in the scalar case,
 $T_{\alpha }^{p}(X) = T_{\beta }^{p}(X)$
for
$T_{\alpha }^{p}(X) = T_{\beta }^{p}(X)$
for
![]() $\alpha ,\beta>0$
when
$\alpha ,\beta>0$
when
![]() $p \in (1,\infty )$
and X has the so-called
$p \in (1,\infty )$
and X has the so-called
![]() $\operatorname {\mathrm {UMD}}$
property (see [Reference Hytönen, van Neerven, Veraar and Weis25, Chapter 4]).
$\operatorname {\mathrm {UMD}}$
property (see [Reference Hytönen, van Neerven, Veraar and Weis25, Chapter 4]).
The scalar-valued definition of
![]() $C(f)$
does not make sense in the vector-valued setting. However, its reformulation using (6.3) does. Following the work of Hytönen and Weis [Reference Hytönen and Weis27], we slightly generalise this formulation. Fix
$C(f)$
does not make sense in the vector-valued setting. However, its reformulation using (6.3) does. Following the work of Hytönen and Weis [Reference Hytönen and Weis27], we slightly generalise this formulation. Fix
![]() $q \in (0,\infty )$
,
$q \in (0,\infty )$
,
![]() $\alpha>0$
, and for a strongly measurable
$\alpha>0$
, and for a strongly measurable
![]() $f \colon \mathbb {R}^{n+1}_{+} \to X$
, define
$f \colon \mathbb {R}^{n+1}_{+} \to X$
, define
 $$ \begin{align*} C_{q}^{(\alpha)}(f)(x):=\sup_{B \ni x} \Big( \frac{1}{\lvert B \rvert} \int_{B} A^{(\alpha)}_{r(B)}(f)^{q} \Big)^{1/q},\qquad x \in \mathbb{R}^{n}. \end{align*} $$
$$ \begin{align*} C_{q}^{(\alpha)}(f)(x):=\sup_{B \ni x} \Big( \frac{1}{\lvert B \rvert} \int_{B} A^{(\alpha)}_{r(B)}(f)^{q} \Big)^{1/q},\qquad x \in \mathbb{R}^{n}. \end{align*} $$
If
![]() $X=\mathbb {R}$
and
$X=\mathbb {R}$
and
![]() $q =2$
, we have
$q =2$
, we have
 $C_{2}^{(\alpha )}(f) \eqsim C(f)$
by (6.3).
$C_{2}^{(\alpha )}(f) \eqsim C(f)$
by (6.3).
The equivalence between
![]() $A^{(\alpha )}(f)$
and
$A^{(\alpha )}(f)$
and
![]() $C^{(\alpha )}(f)$
was proven in [Reference Hytönen and Weis27, Theorem 4.4], using a vector-valued analogue of the good-
$C^{(\alpha )}(f)$
was proven in [Reference Hytönen and Weis27, Theorem 4.4], using a vector-valued analogue of the good-
![]() $\lambda $
inequality (6.5). Since this uses the equivalence of vector-valued tent spaces with different apertures, this result is limited to
$\lambda $
inequality (6.5). Since this uses the equivalence of vector-valued tent spaces with different apertures, this result is limited to
![]() $p \in (1,\infty )$
and
$p \in (1,\infty )$
and
![]() $\operatorname {\mathrm {UMD}}$
Banach spaces.
$\operatorname {\mathrm {UMD}}$
Banach spaces.
As in the scalar-valued setting, we will give a ‘sparse’ proof the equivalence between
![]() $A^{(\alpha )}(f)$
and
$A^{(\alpha )}(f)$
and
![]() $C^{(\alpha )}(f)$
. In the proof we will not use the equivalence of vector-valued tent spaces with different apertures, which allows us the treat
$C^{(\alpha )}(f)$
. In the proof we will not use the equivalence of vector-valued tent spaces with different apertures, which allows us the treat
![]() $p \in (0,\infty )$
and arbitrary Banach spaces. The price we pay is that we have to increase the aperture of
$p \in (0,\infty )$
and arbitrary Banach spaces. The price we pay is that we have to increase the aperture of
![]() $C^{(\alpha )}(f)$
. Of course, if
$C^{(\alpha )}(f)$
. Of course, if
![]() $p \in (1,\infty )$
and X has the
$p \in (1,\infty )$
and X has the
![]() $\operatorname {\mathrm {UMD}}$
property, one can use the equivalence of vector-valued tent spaces with different apertures to recover [Reference Hytönen and Weis27, Theorem 4.4].
$\operatorname {\mathrm {UMD}}$
property, one can use the equivalence of vector-valued tent spaces with different apertures to recover [Reference Hytönen and Weis27, Theorem 4.4].
We refer to [Reference Hytönen, van Neerven, Veraar and Weis26, Chapter 7] for the definition of (Rademacher) type
![]() $r \in [1,2]$
with constant
$r \in [1,2]$
with constant
![]() $\tau _{r,X}$
used in the following theorem. Let us note here that any Banach space has type
$\tau _{r,X}$
used in the following theorem. Let us note here that any Banach space has type
![]() $1$
with constant
$1$
with constant
![]() $\tau _{1,X}=1$
.
$\tau _{1,X}=1$
.
Theorem 6.4. Let X be a Banach space with type
![]() $r \in [1,2]$
, take
$r \in [1,2]$
, take
![]() $q \in (0,\infty )$
and let
$q \in (0,\infty )$
and let
![]() $\alpha>0$
. Let
$\alpha>0$
. Let
![]() $f \colon \mathbb {R}^{n+1}_{+} \to X$
be strongly measurable. For every cube
$f \colon \mathbb {R}^{n+1}_{+} \to X$
be strongly measurable. For every cube
![]() $Q\in \mathcal {Q}$
there exists a
$Q\in \mathcal {Q}$
there exists a
![]() $\frac {1}{2}$
-sparse family
$\frac {1}{2}$
-sparse family
![]() ${\mathcal F}\subset {\mathcal D}(Q)$
such that for a.e.
${\mathcal F}\subset {\mathcal D}(Q)$
such that for a.e.
![]() $x \in Q$
,
$x \in Q$
,
 $$ \begin{align*} A_{\ell_{Q}}^{(\alpha)}(f)(x)\lesssim \tau_{r,X} \Big(\sum_{P\in {\mathcal F}} \Big(\frac{1}{\lvert P \rvert} \int_{P} A_{\ell_{P}}^{(4\alpha+\sqrt{n})}(f)^{q}\Big)^{r/q} \cdot \chi_{P}(x)\Big)^{1/r}. \end{align*} $$
$$ \begin{align*} A_{\ell_{Q}}^{(\alpha)}(f)(x)\lesssim \tau_{r,X} \Big(\sum_{P\in {\mathcal F}} \Big(\frac{1}{\lvert P \rvert} \int_{P} A_{\ell_{P}}^{(4\alpha+\sqrt{n})}(f)^{q}\Big)^{r/q} \cdot \chi_{P}(x)\Big)^{1/r}. \end{align*} $$
Proof. As in the proof of Theorem 6.1, let
![]() $\Phi $
be a smooth function such that
$\Phi $
be a smooth function such that
![]() $\chi _{B(0,1)}\le \Phi \le \chi _{B(0,2)}$
and for
$\chi _{B(0,1)}\le \Phi \le \chi _{B(0,2)}$
and for
![]() $Q \in \mathcal {Q}$
and
$Q \in \mathcal {Q}$
and
![]() $P \in \mathcal {D}(Q)$
define
$P \in \mathcal {D}(Q)$
define
 $$ \begin{align*} f_{Q}(x)&:= \big\|(y,t) \mapsto f(y,t) \cdot \Phi\big(\tfrac{x-y}{\alpha t}\big) \cdot \chi_{(0,\ell_{Q})}(t)\big\|_{\gamma(H,X)}, && x \in Q,\\ f_{P,Q}(x)&:= \big\|(y,t) \mapsto f(y,t) \cdot \Phi\big(\tfrac{x-y}{\alpha t}\big) \cdot \chi_{(\ell_{P},\ell_{Q})}(t)\big\|_{\gamma(H,X)}, && x \in P. \end{align*} $$
$$ \begin{align*} f_{Q}(x)&:= \big\|(y,t) \mapsto f(y,t) \cdot \Phi\big(\tfrac{x-y}{\alpha t}\big) \cdot \chi_{(0,\ell_{Q})}(t)\big\|_{\gamma(H,X)}, && x \in Q,\\ f_{P,Q}(x)&:= \big\|(y,t) \mapsto f(y,t) \cdot \Phi\big(\tfrac{x-y}{\alpha t}\big) \cdot \chi_{(\ell_{P},\ell_{Q})}(t)\big\|_{\gamma(H,X)}, && x \in P. \end{align*} $$
For the family
![]() $\{f_{Q},f_{P,Q}\}_{Q \in \mathcal {Q}, P \in \mathcal {D}(Q)}$
the
$\{f_{Q},f_{P,Q}\}_{Q \in \mathcal {Q}, P \in \mathcal {D}(Q)}$
the
![]() $\ell ^{r}$
-condition holds with
$\ell ^{r}$
-condition holds with
![]() $C_{r} = \tau _{r,X}$
by [Reference Hytönen, van Neerven, Veraar and Weis26, Proposition 9.4.13]. The rest of the proof follows the lines of the proof of Theorem 6.1. The only alterations are the following:
$C_{r} = \tau _{r,X}$
by [Reference Hytönen, van Neerven, Veraar and Weis26, Proposition 9.4.13]. The rest of the proof follows the lines of the proof of Theorem 6.1. The only alterations are the following:
-
• We replace pointwise estimates by the fact that for
 $f \in \gamma (H,X)$
and
$f \in \gamma (H,X)$
and
 $g \in L^{\infty }(\mathbb {R}^{n+1}_{+})$
we have
$g \in L^{\infty }(\mathbb {R}^{n+1}_{+})$
we have  $$ \begin{align*} \lVert f \cdot g \rVert_{\gamma(H,X)} \leq \lVert g \rVert_{L^{\infty}(\mathbb{R}^{n+1}_{+})}\lVert f \rVert_{\gamma(H,X)}. \end{align*} $$
$$ \begin{align*} \lVert f \cdot g \rVert_{\gamma(H,X)} \leq \lVert g \rVert_{L^{\infty}(\mathbb{R}^{n+1}_{+})}\lVert f \rVert_{\gamma(H,X)}. \end{align*} $$
-
• We use Theorem 3.2 with
 $r=r$
instead of
$r=r$
instead of
 $r=2$
.
$r=2$
. -
• In the concluding estimate, we use (2.2) for q instead of
 $2$
.
$2$
.
As in the scalar-valued setting, as a direct corollary of Theorem 6.4, we obtain the following: For
![]() $p,q \in (0,\infty )$
,
$p,q \in (0,\infty )$
,
![]() $\alpha>0$
, a Banach space X and any strongly measurable
$\alpha>0$
, a Banach space X and any strongly measurable
![]() $f \colon \mathbb {R}^{n+1}_{+} \to X$
, we have
$f \colon \mathbb {R}^{n+1}_{+} \to X$
, we have
 $$ \begin{align*} \lVert f \rVert_{T^{p}_{\alpha}(X)} \lesssim \lVert C^{(4\alpha+\sqrt{n})}_{q}(f) \rVert_{L^{p}(\mathbb{R}^{n})}, && p \in (0,\infty). \end{align*} $$
$$ \begin{align*} \lVert f \rVert_{T^{p}_{\alpha}(X)} \lesssim \lVert C^{(4\alpha+\sqrt{n})}_{q}(f) \rVert_{L^{p}(\mathbb{R}^{n})}, && p \in (0,\infty). \end{align*} $$
Moreover, since
 $C_{q}^{(\alpha )}(f)^{q} \lesssim M(A^{(\alpha )}(f)^{q})$
, we have
$C_{q}^{(\alpha )}(f)^{q} \lesssim M(A^{(\alpha )}(f)^{q})$
, we have
 $$ \begin{align*} \lVert C^{(\alpha)}_{q}(f) \rVert_{L^{p}(\mathbb{R}^{n})}&\lesssim \lVert f \rVert_{T^{p}_{\alpha}(X)}, && 0<q<p<\infty. \end{align*} $$
$$ \begin{align*} \lVert C^{(\alpha)}_{q}(f) \rVert_{L^{p}(\mathbb{R}^{n})}&\lesssim \lVert f \rVert_{T^{p}_{\alpha}(X)}, && 0<q<p<\infty. \end{align*} $$
As noted before, this recovers [Reference Hytönen and Weis27, Theorem 4.4] if
![]() $p \in (1,\infty )$
and X is a
$p \in (1,\infty )$
and X is a
![]() $\operatorname {\mathrm {UMD}}$
Banach space.
$\operatorname {\mathrm {UMD}}$
Banach space.
To conclude this subsection, let us note that, doing similar adaptations to the proof of Theorem 6.2 as we did in the proof of Theorem 6.4, we can improve the vector-valued good-
![]() $\lambda $
inequality in [Reference Hytönen and Weis27, Theorem 4.4] to exponential dependence on
$\lambda $
inequality in [Reference Hytönen and Weis27, Theorem 4.4] to exponential dependence on
![]() $\gamma ^{r}$
.
$\gamma ^{r}$
.
7. Vector-valued square functions
In a recent paper by Xu [Reference Xu48], vector-valued Littlewoood–Paley–Stein theory was developed using Littlewood–Paley theory and functional calculus methods, which vastly improves earlier approaches. In this section we will simplify the technical core of [Reference Xu48], using our pointwise sparse domination principle.
To introduce the main result of [Reference Xu48], let
![]() $p \in (1,\infty )$
, let
$p \in (1,\infty )$
, let
![]() $(\Omega ,\mu )$
be a
$(\Omega ,\mu )$
be a
![]() $\sigma $
-finite measure space and let X be a Banach space with martingale cotype
$\sigma $
-finite measure space and let X be a Banach space with martingale cotype
![]() $q \in [2,\infty )$
with constant
$q \in [2,\infty )$
with constant
 $c_{q,X}^{\operatorname {\mathrm {mart}}}$
. We refer to [Reference Hytönen, van Neerven, Veraar and Weis25, Section 3.5.d] for an introduction to martingale (co)type. For a strongly continuous semigroup of regular operators
$c_{q,X}^{\operatorname {\mathrm {mart}}}$
. We refer to [Reference Hytönen, van Neerven, Veraar and Weis25, Section 3.5.d] for an introduction to martingale (co)type. For a strongly continuous semigroup of regular operators
![]() $\{ T_{t} \}_{t\geq 0}$
on
$\{ T_{t} \}_{t\geq 0}$
on
![]() $L^{p}(\Omega )$
and its subordinated Poisson semigroup
$L^{p}(\Omega )$
and its subordinated Poisson semigroup
![]() $\{ P_{t} \}_{t\geq 0}$
, one of the main results of [Reference Xu48] states that for
$\{ P_{t} \}_{t\geq 0}$
, one of the main results of [Reference Xu48] states that for
![]() $f \in L^{p}(\Omega ;X)$
one has
$f \in L^{p}(\Omega ;X)$
one has
 $$ \begin{align} \Big\|\Big(\int_{0}^{\infty} \big\|t \tfrac{\partial}{\partial t}P_{t}(f)\big\|_{X}^{q}\Big)^{1/q}\Big\|_{L^{p}(\Omega)} \lesssim \max\{ p^{\frac1q},p^{\prime} \} \cdot c_{q,X}^{\operatorname{\mathrm{mart}}} \cdot \lVert f \rVert_{L^{p}(\Omega;X)}. \end{align} $$
$$ \begin{align} \Big\|\Big(\int_{0}^{\infty} \big\|t \tfrac{\partial}{\partial t}P_{t}(f)\big\|_{X}^{q}\Big)^{1/q}\Big\|_{L^{p}(\Omega)} \lesssim \max\{ p^{\frac1q},p^{\prime} \} \cdot c_{q,X}^{\operatorname{\mathrm{mart}}} \cdot \lVert f \rVert_{L^{p}(\Omega;X)}. \end{align} $$
The converse of this estimate is shown to hold under a martingale type assumption. Moreover, using functional calculus techniques, similar estimates with
![]() $\{ T_{t} \}_{t\geq 0}$
instead of
$\{ T_{t} \}_{t\geq 0}$
instead of
![]() $\{ P_{t} \}_{t\geq 0}$
are obtained under an analyticity assumption. The growth order in p in most of these estimates is sharp for
$\{ P_{t} \}_{t\geq 0}$
are obtained under an analyticity assumption. The growth order in p in most of these estimates is sharp for
![]() $p \to 1$
and
$p \to 1$
and
![]() $p \to \infty $
. When
$p \to \infty $
. When
![]() $\{ T_{t} \}_{t\geq 0}$
is the heat semigroup on
$\{ T_{t} \}_{t\geq 0}$
is the heat semigroup on
![]() $\mathbb {R}^{n}$
, these results answer a question raised by Naor and Young in the appendix of [Reference Naor and Young43].
$\mathbb {R}^{n}$
, these results answer a question raised by Naor and Young in the appendix of [Reference Naor and Young43].
The most technical part of the argument in [Reference Xu48] is a sharp estimate for a vector-valued variant of the vertical square function. For
![]() $\varepsilon ,\delta>0$
let
$\varepsilon ,\delta>0$
let
![]() $\mathcal {H}_{\varepsilon ,\delta }$
be the class of all
$\mathcal {H}_{\varepsilon ,\delta }$
be the class of all
![]() $\varphi \colon \mathbb {R}^{n} \to \mathbb {R}$
such that
$\varphi \colon \mathbb {R}^{n} \to \mathbb {R}$
such that
 $\int _{\mathbb {R}^{n}} \varphi = 0$
and
$\int _{\mathbb {R}^{n}} \varphi = 0$
and
 $$ \begin{align} \ \ \ \ \ \ \lvert \varphi(x) \rvert &\leq \frac{1}{(1+\lvert x \rvert)^{n+\varepsilon}}, & {\kern28pt} & \ \ x \in \mathbb{R}^{n} \end{align} $$
$$ \begin{align} \ \ \ \ \ \ \lvert \varphi(x) \rvert &\leq \frac{1}{(1+\lvert x \rvert)^{n+\varepsilon}}, & {\kern28pt} & \ \ x \in \mathbb{R}^{n} \end{align} $$
 $$ \begin{align} \lvert \varphi(x)-\varphi(x^{\prime}) \rvert &\leq \frac{\lvert x-x^{\prime} \rvert^{\delta}}{(1+\min\{ \lvert x \rvert,\lvert x^{\prime} \rvert \})^{n+\varepsilon+\delta}}, && x,x^{\prime}\in \mathbb{R}^{n}. \end{align} $$
$$ \begin{align} \lvert \varphi(x)-\varphi(x^{\prime}) \rvert &\leq \frac{\lvert x-x^{\prime} \rvert^{\delta}}{(1+\min\{ \lvert x \rvert,\lvert x^{\prime} \rvert \})^{n+\varepsilon+\delta}}, && x,x^{\prime}\in \mathbb{R}^{n}. \end{align} $$
For
![]() $\varphi \in \mathcal {H}_{\varepsilon ,\delta }$
and
$\varphi \in \mathcal {H}_{\varepsilon ,\delta }$
and
![]() $f \in L^{1}(\mathbb {R}^{n};X)$
, define
$f \in L^{1}(\mathbb {R}^{n};X)$
, define
 $$ \begin{align*} G_{q,\varphi}(f)(x) = \Big(\int_{0}^{\infty}\lVert \varphi_{t} *f(x) \rVert_{X}^{q}\frac{\mathrm{d} t}{t}\Big)^{1/q}, \qquad x \in \mathbb{R}^{n}, \end{align*} $$
$$ \begin{align*} G_{q,\varphi}(f)(x) = \Big(\int_{0}^{\infty}\lVert \varphi_{t} *f(x) \rVert_{X}^{q}\frac{\mathrm{d} t}{t}\Big)^{1/q}, \qquad x \in \mathbb{R}^{n}, \end{align*} $$
where
 $\varphi _{t}(x) = \frac {1}{t^{n}}\varphi (\frac {x}{t})$
. In [Reference Xu48], the main result (7.1) follows from
$\varphi _{t}(x) = \frac {1}{t^{n}}\varphi (\frac {x}{t})$
. In [Reference Xu48], the main result (7.1) follows from
 $$ \begin{align} \lVert G_{q,\varphi}(f) \rVert_{L^{p}(\mathbb{R}^{n})} \lesssim \max\{ p^{\frac1q},p^{\prime} \} \cdot c_{q,X}^{\operatorname{\mathrm{mart}}} \,\lVert f \rVert_{L^{p}(\mathbb{R}^{n};X)}, \end{align} $$
$$ \begin{align} \lVert G_{q,\varphi}(f) \rVert_{L^{p}(\mathbb{R}^{n})} \lesssim \max\{ p^{\frac1q},p^{\prime} \} \cdot c_{q,X}^{\operatorname{\mathrm{mart}}} \,\lVert f \rVert_{L^{p}(\mathbb{R}^{n};X)}, \end{align} $$
by representing the left-hand side of (7.1) for the Poisson semigroup subordinated to the translation group on
![]() $\mathbb {R}$
by
$\mathbb {R}$
by
![]() $G_{q,\varphi }(f)$
for some
$G_{q,\varphi }(f)$
for some
 $\varphi \in \mathcal {H}_{\frac 12,1}$
and then using a transference argument for general semigroups.
$\varphi \in \mathcal {H}_{\frac 12,1}$
and then using a transference argument for general semigroups.
The case
![]() $p < q$
of (7.4) follows quite easily from the case
$p < q$
of (7.4) follows quite easily from the case
![]() $p=q$
, using classical Calderón–Zygmund theory. The case
$p=q$
, using classical Calderón–Zygmund theory. The case
![]() $p>q$
with optimal dependence on p is harder, for which delicate results on conical and intrinsic square functions and weighted estimates, developed in the scalar-valued case by Wilson [Reference Wilson46, Reference Wilson47], are adapted to the vector-valued setting in [Reference Xu48, Section 6]. We will prove (7.4) without the use of this machinery, instead opting to use our sparse domination principle.
$p>q$
with optimal dependence on p is harder, for which delicate results on conical and intrinsic square functions and weighted estimates, developed in the scalar-valued case by Wilson [Reference Wilson46, Reference Wilson47], are adapted to the vector-valued setting in [Reference Xu48, Section 6]. We will prove (7.4) without the use of this machinery, instead opting to use our sparse domination principle.
As a starting point, we will use the following weak
![]() $L^{1}$
-estimate for
$L^{1}$
-estimate for
![]() $G_{q,\varphi }$
, which is implicitly contained in [Reference Xu48].
$G_{q,\varphi }$
, which is implicitly contained in [Reference Xu48].
Proposition 7.1. Let
![]() $q \in [2,\infty )$
, let X be a Banach space with martingale cotype q and let
$q \in [2,\infty )$
, let X be a Banach space with martingale cotype q and let
![]() $\varphi \in \mathcal {H}_{\varepsilon ,\delta }$
for
$\varphi \in \mathcal {H}_{\varepsilon ,\delta }$
for
![]() $\varepsilon ,\delta>0$
. Then we have for
$\varepsilon ,\delta>0$
. Then we have for
![]() $f \in L^{1}(\mathbb {R}^{n};X)$
,
$f \in L^{1}(\mathbb {R}^{n};X)$
,
 $$ \begin{align*} \lVert G_{q,\varphi}(f) \rVert_{L^{1,\infty}(\mathbb{R}^{n})} \lesssim c_{q,X}^{\operatorname{\mathrm{mart}}} \,\lVert f \rVert_{L^{1}(\mathbb{R}^{n};X)}, \end{align*} $$
$$ \begin{align*} \lVert G_{q,\varphi}(f) \rVert_{L^{1,\infty}(\mathbb{R}^{n})} \lesssim c_{q,X}^{\operatorname{\mathrm{mart}}} \,\lVert f \rVert_{L^{1}(\mathbb{R}^{n};X)}, \end{align*} $$
with the implicit constant only depending on
![]() $\varepsilon ,\delta ,n$
.
$\varepsilon ,\delta ,n$
.
Proof. The estimate
 $$ \begin{align*} \lVert G_{q,\varphi}(f) \rVert_{L^{q}(\mathbb{R}^{n})} \lesssim c_{q,X}^{\operatorname{\mathrm{mart}}} \,\lVert f \rVert_{L^{q}(\mathbb{R}^{n};X)} \end{align*} $$
$$ \begin{align*} \lVert G_{q,\varphi}(f) \rVert_{L^{q}(\mathbb{R}^{n})} \lesssim c_{q,X}^{\operatorname{\mathrm{mart}}} \,\lVert f \rVert_{L^{q}(\mathbb{R}^{n};X)} \end{align*} $$
follows directly from [Reference Xu48, Lemma 5.6], see the first half of Step 1 of the proof of [Reference Xu48, Theorem 1.5]. The proposition then follows by viewing
![]() $G_{q,\varphi }$
as a Calderón–Zygmund operator using [Reference Xu48, Lemma 5.4].
$G_{q,\varphi }$
as a Calderón–Zygmund operator using [Reference Xu48, Lemma 5.4].
For
![]() $\varphi \in \mathcal {H}_{\varepsilon ,\delta }$
for
$\varphi \in \mathcal {H}_{\varepsilon ,\delta }$
for
![]() $\varepsilon ,\delta>0$
, define the localisation
$\varepsilon ,\delta>0$
, define the localisation
 $$ \begin{align*} G_{q,\varphi}^{h}(f)(x) = \Big(\int_{0}^{h}\lVert \varphi_{t} *f(x) \rVert_{X}^{q}\frac{\mathrm{d} t}{t}\Big)^{1/q}, \qquad x \in \mathbb{R}^{n} \end{align*} $$
$$ \begin{align*} G_{q,\varphi}^{h}(f)(x) = \Big(\int_{0}^{h}\lVert \varphi_{t} *f(x) \rVert_{X}^{q}\frac{\mathrm{d} t}{t}\Big)^{1/q}, \qquad x \in \mathbb{R}^{n} \end{align*} $$
for
![]() $h>0$
. Since the support of
$h>0$
. Since the support of
![]() $\varphi $
is not necessarily compact, the support of
$\varphi $
is not necessarily compact, the support of
 $G_{q,\varphi }^{h}(f)$
is not localised to (a multiple of) the support of f. Therefore, for arbitrary
$G_{q,\varphi }^{h}(f)$
is not localised to (a multiple of) the support of f. Therefore, for arbitrary
![]() $f \in L^{1}(\mathbb {R}^{d};X)$
, one cannot estimate
$f \in L^{1}(\mathbb {R}^{d};X)$
, one cannot estimate
 $G_{q,\varphi }^{h}(f)$
by a local expression of the form
$G_{q,\varphi }^{h}(f)$
by a local expression of the form
 $$ \begin{align} \Big(\sum_{P \in \mathcal{F}} \big\langle\lVert f \rVert_{X}\big\rangle_{1,\alpha P}^{q} \chi_{P}\Big)^{1/q}, \qquad \alpha \geq 1.\\[-15pt]\nonumber \end{align} $$
$$ \begin{align} \Big(\sum_{P \in \mathcal{F}} \big\langle\lVert f \rVert_{X}\big\rangle_{1,\alpha P}^{q} \chi_{P}\Big)^{1/q}, \qquad \alpha \geq 1.\\[-15pt]\nonumber \end{align} $$
This, in particular, means that the precursor of Theorem 3.2 in [Reference Lorist39] – that is, Theorem 4.2 – is not applicable to the localisation
 $G_{q,\varphi }^{\ell _{Q}}(f)$
.
$G_{q,\varphi }^{\ell _{Q}}(f)$
.
Thanks to the flexible formulation of Theorem 3.2, we are able to compensate the nonlocal behaviour of
 $G_{q,\varphi }^{h}(f)$
by adding a convergent series of dilations of P to (7.5). The main result of this section reads as follows.
$G_{q,\varphi }^{h}(f)$
by adding a convergent series of dilations of P to (7.5). The main result of this section reads as follows.
Theorem 7.2. Let
![]() $q \in [2,\infty )$
, let X be a Banach space with martingale cotype q and let
$q \in [2,\infty )$
, let X be a Banach space with martingale cotype q and let
![]() $\varphi \in \mathcal {H}_{\varepsilon ,\delta }$
with
$\varphi \in \mathcal {H}_{\varepsilon ,\delta }$
with
![]() $\varepsilon ,\delta>0$
. For any
$\varepsilon ,\delta>0$
. For any
![]() $f \in L^{1}(\mathbb {R}^{n};X)$
and
$f \in L^{1}(\mathbb {R}^{n};X)$
and
![]() $Q \in \mathcal {Q}$
there exists a
$Q \in \mathcal {Q}$
there exists a
![]() $\frac {1}{2}$
-sparse collection of cubes
$\frac {1}{2}$
-sparse collection of cubes
![]() $\mathcal {F} \subset \mathcal {D}(Q)$
such that for a.e.
$\mathcal {F} \subset \mathcal {D}(Q)$
such that for a.e.
![]() $x \in Q$
,
$x \in Q$
,
 $$ \begin{align*} G_{q,\varphi}^{\ell_{Q}}(f)(x) \lesssim c_{q,X}^{\operatorname{\mathrm{mart}}} \Big(\sum_{P \in \mathcal{F}} \sum_{m=1}^{\infty} \frac{1}{2^{m\varepsilon}}\big\langle\lVert f \rVert_{X}\big\rangle_{1,2^{m}P}^{q} \chi_{P}(x)\Big)^{1/q},\\[-15pt] \end{align*} $$
$$ \begin{align*} G_{q,\varphi}^{\ell_{Q}}(f)(x) \lesssim c_{q,X}^{\operatorname{\mathrm{mart}}} \Big(\sum_{P \in \mathcal{F}} \sum_{m=1}^{\infty} \frac{1}{2^{m\varepsilon}}\big\langle\lVert f \rVert_{X}\big\rangle_{1,2^{m}P}^{q} \chi_{P}(x)\Big)^{1/q},\\[-15pt] \end{align*} $$
with the implicit constant depending only on
![]() $\varepsilon ,\delta ,n$
.
$\varepsilon ,\delta ,n$
.
Using Hölder’s inequality and the boundedness of the maximal operator, Theorem 7.2 yields for
![]() $p>q$
and any
$p>q$
and any
![]() $g \in L^{(p/q)^{\prime }}(\mathbb {R}^{n})$
that
$g \in L^{(p/q)^{\prime }}(\mathbb {R}^{n})$
that
 $$ \begin{align*} \int_{Q} G_{q,\varphi}^{\ell_{Q}}(f)^{q} g&\lesssim (c_{q,X}^{\operatorname{\mathrm{mart}}})^{q}\sum_{P \in \mathcal{F}} \sum_{m=1}^{\infty} \frac{1}{2^{m\varepsilon}}\big\langle\lVert f \rVert_{X}\big\rangle_{1,2^{m}P}^{q} \int_{P} g\\ &\lesssim (c_{q,X}^{\operatorname{\mathrm{mart}}})^{q} \sum_{P \in \mathcal{F}} \int_{E_{P}} M\big(\lVert f \rVert_{X} \big)^{q} Mg\\ &\lesssim (c_{q,X}^{\operatorname{\mathrm{mart}}})^{q} \cdot \frac{p}{q} \cdot \lVert f \rVert_{L^{p}(\mathbb{R}^{n};X)}^{q} \lVert g \rVert_{L^{(p/q)^{\prime}}(\mathbb{R}^{n})}.\\[-15pt] \end{align*} $$
$$ \begin{align*} \int_{Q} G_{q,\varphi}^{\ell_{Q}}(f)^{q} g&\lesssim (c_{q,X}^{\operatorname{\mathrm{mart}}})^{q}\sum_{P \in \mathcal{F}} \sum_{m=1}^{\infty} \frac{1}{2^{m\varepsilon}}\big\langle\lVert f \rVert_{X}\big\rangle_{1,2^{m}P}^{q} \int_{P} g\\ &\lesssim (c_{q,X}^{\operatorname{\mathrm{mart}}})^{q} \sum_{P \in \mathcal{F}} \int_{E_{P}} M\big(\lVert f \rVert_{X} \big)^{q} Mg\\ &\lesssim (c_{q,X}^{\operatorname{\mathrm{mart}}})^{q} \cdot \frac{p}{q} \cdot \lVert f \rVert_{L^{p}(\mathbb{R}^{n};X)}^{q} \lVert g \rVert_{L^{(p/q)^{\prime}}(\mathbb{R}^{n})}.\\[-15pt] \end{align*} $$
This yields (7.4) by duality and the monotone convergence theorem.
Moreover, one can deduce sharp weighted estimates for
![]() $G_{q,\varphi }(f)$
for weights in the Muckenhoupt
$G_{q,\varphi }(f)$
for weights in the Muckenhoupt
![]() $A_{p}$
-class, using [Reference Lerner34, Lemma 4.5] and an argument as in [Reference Lerner33, Section 4].
$A_{p}$
-class, using [Reference Lerner34, Lemma 4.5] and an argument as in [Reference Lerner33, Section 4].
Proof of Theorem 7.2
For
![]() $Q \in \mathcal {Q}$
and
$Q \in \mathcal {Q}$
and
![]() $P \in \mathcal {D}(Q)$
define
$P \in \mathcal {D}(Q)$
define
 $$ \begin{align*} f_{Q}(x) &:= G_{q,\varphi}^{\ell_{Q}}(f)(x),&& x \in \mathbb{R}^{n},\\ f_{P,Q}(x) &:= \Big(\int_{\ell_{P}}^{\ell_{Q}}\lVert \varphi_{t} *f(x) \rVert_{X}^{q}\frac{\mathrm{d} t}{t}\Big)^{1/q},&& x \in \mathbb{R}^{n}.\\[-15pt] \end{align*} $$
$$ \begin{align*} f_{Q}(x) &:= G_{q,\varphi}^{\ell_{Q}}(f)(x),&& x \in \mathbb{R}^{n},\\ f_{P,Q}(x) &:= \Big(\int_{\ell_{P}}^{\ell_{Q}}\lVert \varphi_{t} *f(x) \rVert_{X}^{q}\frac{\mathrm{d} t}{t}\Big)^{1/q},&& x \in \mathbb{R}^{n}.\\[-15pt] \end{align*} $$
The family
![]() $\{f_{Q},f_{P,Q}\}_{Q \in \mathcal {Q}, P \in \mathcal {D}(Q)}$
trivially satisfies the
$\{f_{Q},f_{P,Q}\}_{Q \in \mathcal {Q}, P \in \mathcal {D}(Q)}$
trivially satisfies the
![]() $\ell ^{q}$
-condition with
$\ell ^{q}$
-condition with
![]() $C_{q}=1$
, and condition (3.1) holds as well. Therefore, by Theorem 3.2, there exists a
$C_{q}=1$
, and condition (3.1) holds as well. Therefore, by Theorem 3.2, there exists a
![]() $\frac {1}{2}$
-sparse family
$\frac {1}{2}$
-sparse family
![]() ${\mathcal F}\subset {\mathcal D}(Q)$
such that
${\mathcal F}\subset {\mathcal D}(Q)$
such that
 $$ \begin{align*} G_{q,\varphi}^{\ell_{Q}}(f)(x)\lesssim \Big(\sum_{P\in {\mathcal F}}\gamma_{P}^{q}\chi_{P}(x)\Big)^{1/q},\qquad x\in Q.\\[-15pt] \end{align*} $$
$$ \begin{align*} G_{q,\varphi}^{\ell_{Q}}(f)(x)\lesssim \Big(\sum_{P\in {\mathcal F}}\gamma_{P}^{q}\chi_{P}(x)\Big)^{1/q},\qquad x\in Q.\\[-15pt] \end{align*} $$
Thus, it suffices to show
 $$ \begin{align} \gamma_{P} \lesssim c_{q,X}^{\operatorname{\mathrm{mart}}} \cdot \Big( \sum_{m=1}^{\infty} \frac{1}{2^{m\varepsilon}}\big\langle\lVert f \rVert_{X}\big\rangle_{1,2^{m}P}^{q}\Big)^{1/q}:= c_{q,X}^{\operatorname{\mathrm{mart}}} \cdot \mathcal{M}_{P}\\[-15pt]\nonumber \end{align} $$
$$ \begin{align} \gamma_{P} \lesssim c_{q,X}^{\operatorname{\mathrm{mart}}} \cdot \Big( \sum_{m=1}^{\infty} \frac{1}{2^{m\varepsilon}}\big\langle\lVert f \rVert_{X}\big\rangle_{1,2^{m}P}^{q}\Big)^{1/q}:= c_{q,X}^{\operatorname{\mathrm{mart}}} \cdot \mathcal{M}_{P}\\[-15pt]\nonumber \end{align} $$
for
![]() $P \in \mathcal {F}$
.
$P \in \mathcal {F}$
.
Fix
![]() $P \in \mathcal {F}$
. For any
$P \in \mathcal {F}$
. For any
![]() $z \in P$
we have by (7.2) and Hölder’s inequality
$z \in P$
we have by (7.2) and Hölder’s inequality
 $$ \begin{align} \begin{aligned} G_{q,\varphi}^{\ell_{P}}(f\chi_{\mathbb{R}^{n} \setminus 2P})(z) &\leq \Big(\int_{0}^{\ell_{P}} \Big(\sum_{m=1}^{\infty}\int_{(2^{m+1}P)\setminus (2^{m}P)} \frac{1}{{\lvert z-y \rvert}^{d+\varepsilon}} \lVert f(y) \rVert_{X} \,\mathrm{d} y\Big)^{q}\frac{\mathrm{d} t}{t^{1-q\varepsilon}}\Big)^{\frac1q}\\ &\lesssim \sum_{m=2}^{\infty} \frac{1}{2^{m\varepsilon}}\big\langle\lVert f \rVert_{X}\big\rangle_{1,2^{m}Q}\cdot \Big(\ell_{P}^{-q\varepsilon} \int_{0}^{\ell_{P}} \frac{\mathrm{d} t}{t^{1-q\varepsilon}}\Big)^{\frac1q} \lesssim \mathcal{M}_{P}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} G_{q,\varphi}^{\ell_{P}}(f\chi_{\mathbb{R}^{n} \setminus 2P})(z) &\leq \Big(\int_{0}^{\ell_{P}} \Big(\sum_{m=1}^{\infty}\int_{(2^{m+1}P)\setminus (2^{m}P)} \frac{1}{{\lvert z-y \rvert}^{d+\varepsilon}} \lVert f(y) \rVert_{X} \,\mathrm{d} y\Big)^{q}\frac{\mathrm{d} t}{t^{1-q\varepsilon}}\Big)^{\frac1q}\\ &\lesssim \sum_{m=2}^{\infty} \frac{1}{2^{m\varepsilon}}\big\langle\lVert f \rVert_{X}\big\rangle_{1,2^{m}Q}\cdot \Big(\ell_{P}^{-q\varepsilon} \int_{0}^{\ell_{P}} \frac{\mathrm{d} t}{t^{1-q\varepsilon}}\Big)^{\frac1q} \lesssim \mathcal{M}_{P}. \end{aligned} \end{align} $$
Therefore, we have by the weak
![]() $L^{1}$
-boundedness of
$L^{1}$
-boundedness of
![]() $G_{q,\varphi }$
in Proposition 7.1 that
$G_{q,\varphi }$
in Proposition 7.1 that
 $$ \begin{align*} (f_{P}\chi_{P})^{*}(|P|/2^{n+3}) &\lesssim \big(G_{q,\varphi}(f\chi_{2P})\chi_{P}\big)^{*}(|P|/2^{n+3}) + \mathcal{M}_{P}\\ &\lesssim c_{q,X}^{\operatorname{\mathrm{mart}}} \cdot \big\langle\lVert f \rVert_{X}\big\rangle_{1,2P} +\mathcal{M}_{P} \lesssim \,c_{q,X}^{\operatorname{\mathrm{mart}}} \cdot \mathcal{M}_{P}. \end{align*} $$
$$ \begin{align*} (f_{P}\chi_{P})^{*}(|P|/2^{n+3}) &\lesssim \big(G_{q,\varphi}(f\chi_{2P})\chi_{P}\big)^{*}(|P|/2^{n+3}) + \mathcal{M}_{P}\\ &\lesssim c_{q,X}^{\operatorname{\mathrm{mart}}} \cdot \big\langle\lVert f \rVert_{X}\big\rangle_{1,2P} +\mathcal{M}_{P} \lesssim \,c_{q,X}^{\operatorname{\mathrm{mart}}} \cdot \mathcal{M}_{P}. \end{align*} $$
Now let us turn to
 $(m^{\#}_{P}f)^{*}(|P|/2^{n+3})$
. Fix
$(m^{\#}_{P}f)^{*}(|P|/2^{n+3})$
. Fix
![]() $x \in P$
and
$x \in P$
and
![]() $R \in \mathcal {D}(P)$
such that
$R \in \mathcal {D}(P)$
such that
![]() $x \in R$
. We will split
$x \in R$
. We will split
For
![]() $\xi ,\eta \in R$
we note that by (7.3) and [Reference Grafakos17, Theorem 2.1.10] we have
$\xi ,\eta \in R$
we note that by (7.3) and [Reference Grafakos17, Theorem 2.1.10] we have
 $$ \begin{align*} \Big(\int_{\ell_{R}}^{\ell_{P}}\big\|\varphi_{t} *f\chi_{2P\setminus 2R}&(\xi)-\varphi_{t} *f\chi_{2P\setminus 2R}(\eta)\big\|_{X}^{q}\frac{\mathrm{d} t}{t}\Big)^{1/q}\\ &\lesssim \Big(\int_{\ell_{R}}^{\ell_{P}} \Big( \lvert \xi-\eta \rvert^{\delta} \int_{\mathbb{R}^{n}\setminus B(x,{\ell_{R}/2})}\frac{\lVert f(y)\chi_{2P}(y) \rVert_{X}}{\lvert x-y \rvert^{n+\frac{\delta}{2}}}\,\mathrm{d} y\Big)^{q} \frac{\mathrm{d} t}{t^{1+\frac{\delta}{2}}}\Big)^{1/q}\\ &\lesssim \ell_{R}^{\delta} \cdot \Big\|\frac{\chi_{\mathbb{R}\setminus B(0,\ell_{R}/2)}}{\lvert \cdot \rvert^{n+\frac{\delta}{2}}}\Big\|_{L^{1}(\mathbb{R}^{n})} \cdot \int_{\ell_{R}}^{\ell_{P}} \frac{\mathrm{d} t}{t^{1+\frac{\delta}{2}}}\cdot M\big(\lVert f\chi_{2P} \rVert_{X} \big)(x)\\ &\lesssim M\big(\lVert f\chi_{2P} \rVert_{X} \big)(x). \end{align*} $$
$$ \begin{align*} \Big(\int_{\ell_{R}}^{\ell_{P}}\big\|\varphi_{t} *f\chi_{2P\setminus 2R}&(\xi)-\varphi_{t} *f\chi_{2P\setminus 2R}(\eta)\big\|_{X}^{q}\frac{\mathrm{d} t}{t}\Big)^{1/q}\\ &\lesssim \Big(\int_{\ell_{R}}^{\ell_{P}} \Big( \lvert \xi-\eta \rvert^{\delta} \int_{\mathbb{R}^{n}\setminus B(x,{\ell_{R}/2})}\frac{\lVert f(y)\chi_{2P}(y) \rVert_{X}}{\lvert x-y \rvert^{n+\frac{\delta}{2}}}\,\mathrm{d} y\Big)^{q} \frac{\mathrm{d} t}{t^{1+\frac{\delta}{2}}}\Big)^{1/q}\\ &\lesssim \ell_{R}^{\delta} \cdot \Big\|\frac{\chi_{\mathbb{R}\setminus B(0,\ell_{R}/2)}}{\lvert \cdot \rvert^{n+\frac{\delta}{2}}}\Big\|_{L^{1}(\mathbb{R}^{n})} \cdot \int_{\ell_{R}}^{\ell_{P}} \frac{\mathrm{d} t}{t^{1+\frac{\delta}{2}}}\cdot M\big(\lVert f\chi_{2P} \rVert_{X} \big)(x)\\ &\lesssim M\big(\lVert f\chi_{2P} \rVert_{X} \big)(x). \end{align*} $$
Furthermore, by (7.2) we have for
![]() $\xi \in R$
$\xi \in R$
 $$ \begin{align*} \Big(\int_{\ell_{R}}^{\ell_{P}}\big\|\varphi_{t} *f\chi_{2R}(\xi)\big\|_{X}^{q}\frac{\mathrm{d} t}{t}\Big)^{1/q} &\leq \int_{2R} \lVert f(y) \rVert_{X} \,\mathrm{d} y\cdot \Big(\int_{\ell_{R}}^{\ell_{P}}\frac{\mathrm{d} t}{t^{1+qn}}\Big)^{1/q}\\ &\lesssim M\big(\lVert f\chi_{2P} \rVert_{X} \big)(x). \end{align*} $$
$$ \begin{align*} \Big(\int_{\ell_{R}}^{\ell_{P}}\big\|\varphi_{t} *f\chi_{2R}(\xi)\big\|_{X}^{q}\frac{\mathrm{d} t}{t}\Big)^{1/q} &\leq \int_{2R} \lVert f(y) \rVert_{X} \,\mathrm{d} y\cdot \Big(\int_{\ell_{R}}^{\ell_{P}}\frac{\mathrm{d} t}{t^{1+qn}}\Big)^{1/q}\\ &\lesssim M\big(\lVert f\chi_{2P} \rVert_{X} \big)(x). \end{align*} $$
Splitting as in (7.8), combining these estimates with (7.7) and using the weak
![]() $L^{1}$
-boundedness of the maximal operator, we therefore obtain
$L^{1}$
-boundedness of the maximal operator, we therefore obtain
 $$ \begin{align*} (m^{\#}_{P}f)^{*}(|P|/2^{n+3})&\lesssim \big(M(\lVert f\chi_{2P} \rVert_{X})\big)^{*}(|P|/2^{n+3}) +\mathcal{M}_{P}\\ &\lesssim \big\langle\lVert f \rVert_{X}\big\rangle_{1,2P} +\mathcal{M}_{P} \lesssim \mathcal{M}_{P}. \end{align*} $$
$$ \begin{align*} (m^{\#}_{P}f)^{*}(|P|/2^{n+3})&\lesssim \big(M(\lVert f\chi_{2P} \rVert_{X})\big)^{*}(|P|/2^{n+3}) +\mathcal{M}_{P}\\ &\lesssim \big\langle\lVert f \rVert_{X}\big\rangle_{1,2P} +\mathcal{M}_{P} \lesssim \mathcal{M}_{P}. \end{align*} $$
This finishes the proof of (7.6) and thus the proof of the theorem.
8. An application to dyadic sums
In this final section we will give a condition on a sequence
![]() $\{\alpha _{R}\}_{R\in {\mathcal D}(Q)}$
for
$\{\alpha _{R}\}_{R\in {\mathcal D}(Q)}$
for
![]() $Q \in \mathcal {Q}$
that allows one to control a dyadic sum of the form
$Q \in \mathcal {Q}$
that allows one to control a dyadic sum of the form
![]() $\sum _{R\in {\mathcal D}(Q)}\alpha _{R}\chi _{R}$
by a sum over a sparse family
$\sum _{R\in {\mathcal D}(Q)}\alpha _{R}\chi _{R}$
by a sum over a sparse family
![]() ${\mathcal F}\subset {\mathcal D}(Q)$
. As an application, we will generalise and provide a new proof of a good-
${\mathcal F}\subset {\mathcal D}(Q)$
. As an application, we will generalise and provide a new proof of a good-
![]() $\lambda $
inequality of Honzík and Jaye [Reference Honzík and Jaye21].
$\lambda $
inequality of Honzík and Jaye [Reference Honzík and Jaye21].
Theorem 8.1. Let
![]() $Q\in {\mathcal Q}$
and let
$Q\in {\mathcal Q}$
and let
![]() $\{\alpha _{R}\}_{R\in {\mathcal D}(Q)}$
be a sequence of nonnegative numbers. Suppose that there exist
$\{\alpha _{R}\}_{R\in {\mathcal D}(Q)}$
be a sequence of nonnegative numbers. Suppose that there exist
![]() $C>0$
and
$C>0$
and
![]() $0<\delta \le 1$
such that for every cube
$0<\delta \le 1$
such that for every cube
![]() $Q^{\prime }\in {\mathcal D}(Q)$
,
$Q^{\prime }\in {\mathcal D}(Q)$
,
 $$ \begin{align} \sum_{R\in {\mathcal D}(Q^{\prime})}\alpha_{R}^{\delta}|R|\le C\alpha_{Q^{\prime}}^{\delta}|Q^{\prime}|. \end{align} $$
$$ \begin{align} \sum_{R\in {\mathcal D}(Q^{\prime})}\alpha_{R}^{\delta}|R|\le C\alpha_{Q^{\prime}}^{\delta}|Q^{\prime}|. \end{align} $$
Then there exists a
![]() $\frac {1}{2}$
-sparse family
$\frac {1}{2}$
-sparse family
![]() ${\mathcal F}\subset {\mathcal D}(Q)$
such that for a.e.
${\mathcal F}\subset {\mathcal D}(Q)$
such that for a.e.
![]() $x\in Q$
,
$x\in Q$
,
 $$ \begin{align*} \sum_{R\in {\mathcal D}(Q)}\alpha_{R}\chi_{R}(x)\lesssim C \,\sum_{P\in {\mathcal F}}\alpha_{P}\chi_{P}(x). \end{align*} $$
$$ \begin{align*} \sum_{R\in {\mathcal D}(Q)}\alpha_{R}\chi_{R}(x)\lesssim C \,\sum_{P\in {\mathcal F}}\alpha_{P}\chi_{P}(x). \end{align*} $$
Proof. For
![]() $Q^{\prime } \in \mathcal {D}(Q)$
denote
$Q^{\prime } \in \mathcal {D}(Q)$
denote
 $$ \begin{align*} f_{Q^{\prime}}(x)=\sum_{R\in {\mathcal D}(Q^{\prime})}\alpha_{R}\chi_{R}(x), \qquad x \in Q^{\prime}, \end{align*} $$
$$ \begin{align*} f_{Q^{\prime}}(x)=\sum_{R\in {\mathcal D}(Q^{\prime})}\alpha_{R}\chi_{R}(x), \qquad x \in Q^{\prime}, \end{align*} $$
and for
![]() $P\in \mathcal {D}(Q^{\prime })$
set
$P\in \mathcal {D}(Q^{\prime })$
set
![]() $f_{P,Q^{\prime }}=f_{Q^{\prime }}-f_{P}$
. Then
$f_{P,Q^{\prime }}=f_{Q^{\prime }}-f_{P}$
. Then
![]() $\{f_{Q^{\prime }},f_{P,Q^{\prime }}\}_{Q^{\prime } \in \mathcal {D}(Q), P \in \mathcal {D}(Q^{\prime })}$
trivially satisfies the
$\{f_{Q^{\prime }},f_{P,Q^{\prime }}\}_{Q^{\prime } \in \mathcal {D}(Q), P \in \mathcal {D}(Q^{\prime })}$
trivially satisfies the
![]() $\ell ^{1}$
-condition (with
$\ell ^{1}$
-condition (with
![]() $C_{1}=1$
) and condition (3.1).
$C_{1}=1$
) and condition (3.1).
Observe that
![]() $f_{P,Q}$
is a constant on P and therefore
$f_{P,Q}$
is a constant on P and therefore
 $m_{P}^{\#}f\equiv 0$
. Hence, by the local version of Theorem 3.2 (see Remark 3.3), there exists a
$m_{P}^{\#}f\equiv 0$
. Hence, by the local version of Theorem 3.2 (see Remark 3.3), there exists a
![]() $\frac {1}{2}$
-sparse family
$\frac {1}{2}$
-sparse family
![]() ${\mathcal F}\subset {\mathcal D}(Q)$
such that, for a.e.
${\mathcal F}\subset {\mathcal D}(Q)$
such that, for a.e.
![]() $x\in Q$
,
$x\in Q$
,
 $$ \begin{align*} \sum_{R\in {\mathcal D}(Q)}\lambda_{R}\chi_{R}(x)\le \sum_{P\in {\mathcal F}}(f_{P}\chi_{P})^{*}(|P|/2^{n+3})\chi_{P}(x). \end{align*} $$
$$ \begin{align*} \sum_{R\in {\mathcal D}(Q)}\lambda_{R}\chi_{R}(x)\le \sum_{P\in {\mathcal F}}(f_{P}\chi_{P})^{*}(|P|/2^{n+3})\chi_{P}(x). \end{align*} $$
By (2.2),
 $$ \begin{align*} (f_{P}\chi_{P})^{*}(|P|/2^{n+3})\le \Big(\frac{2^{n+3}}{|P|}\int_{P}f_{P}^{\delta}\Big)^{1/\delta} \end{align*} $$
$$ \begin{align*} (f_{P}\chi_{P})^{*}(|P|/2^{n+3})\le \Big(\frac{2^{n+3}}{|P|}\int_{P}f_{P}^{\delta}\Big)^{1/\delta} \end{align*} $$
and, by (8.1),
 $$ \begin{align*} \int_{P}f_{P}^{\delta}\le \sum_{R\in {\mathcal D}(P)}\alpha_{R}^{\delta}|R|\le C\alpha_{P}^{\delta}|P|. \end{align*} $$
$$ \begin{align*} \int_{P}f_{P}^{\delta}\le \sum_{R\in {\mathcal D}(P)}\alpha_{R}^{\delta}|R|\le C\alpha_{P}^{\delta}|P|. \end{align*} $$
Combining these three estimates completes the proof.
Let
![]() ${\mathscr D}$
be a dyadic lattice in
${\mathscr D}$
be a dyadic lattice in
![]() ${\mathbb R}^{n}$
. Given a sequence of nonnegative numbers
${\mathbb R}^{n}$
. Given a sequence of nonnegative numbers
![]() $\boldsymbol {\alpha }=\{\alpha _{Q}\}_{Q\in {\mathscr D}}$
, define the following two objects associated with
$\boldsymbol {\alpha }=\{\alpha _{Q}\}_{Q\in {\mathscr D}}$
, define the following two objects associated with
![]() $\boldsymbol {\alpha }$
:
$\boldsymbol {\alpha }$
:
 $$ \begin{align*} S_{q}(\boldsymbol{\alpha})&:=\Big(\sum_{Q\in {\mathscr D}}\alpha_{Q}^{q}\chi_{Q}\Big)^{1/q}\qquad q \in (0,\infty),\\ M({\boldsymbol{\alpha}})&:=\sup_{Q\in {\mathscr D}}\alpha_{Q}\chi_{Q}. \end{align*} $$
$$ \begin{align*} S_{q}(\boldsymbol{\alpha})&:=\Big(\sum_{Q\in {\mathscr D}}\alpha_{Q}^{q}\chi_{Q}\Big)^{1/q}\qquad q \in (0,\infty),\\ M({\boldsymbol{\alpha}})&:=\sup_{Q\in {\mathscr D}}\alpha_{Q}\chi_{Q}. \end{align*} $$
Corollary 8.2. Let
![]() $q \in (0,\infty )$
. Suppose that there exist
$q \in (0,\infty )$
. Suppose that there exist
![]() $C>0$
and
$C>0$
and
![]() $0<\delta \le q$
such that for every cube
$0<\delta \le q$
such that for every cube
![]() $Q\in {\mathscr D}$
,
$Q\in {\mathscr D}$
,
 $$ \begin{align} \sum_{R\in {\mathcal D}(Q)}\alpha_{R}^{\delta}|R|\le C\alpha_{Q}^{\delta}|Q|. \end{align} $$
$$ \begin{align} \sum_{R\in {\mathcal D}(Q)}\alpha_{R}^{\delta}|R|\le C\alpha_{Q}^{\delta}|Q|. \end{align} $$
Then there exists
![]() $K=K(q,\delta ,C)$
such that for all
$K=K(q,\delta ,C)$
such that for all
![]() $\lambda>0$
and
$\lambda>0$
and
![]() $0<\varepsilon <1$
,
$0<\varepsilon <1$
,
 $$ \begin{align} \begin{aligned} \big|\{x \in \mathbb{R}^{n}:S_{q}(\boldsymbol{\alpha})(x)>&2\lambda, M(\boldsymbol{\alpha})(x)\le \varepsilon\lambda\}\big| \le 2e^{-K/\varepsilon^{q}}\big|\{x\in \mathbb{R}^{n}:S_{q}(\boldsymbol{\alpha})(x)>\lambda\}\big|. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \big|\{x \in \mathbb{R}^{n}:S_{q}(\boldsymbol{\alpha})(x)>&2\lambda, M(\boldsymbol{\alpha})(x)\le \varepsilon\lambda\}\big| \le 2e^{-K/\varepsilon^{q}}\big|\{x\in \mathbb{R}^{n}:S_{q}(\boldsymbol{\alpha})(x)>\lambda\}\big|. \end{aligned} \end{align} $$
Proof. By a standard limiting argument, it sufficed to prove (8.3) for
 $S^{F}_{q}(A)$
instead of
$S^{F}_{q}(A)$
instead of
![]() $S_{q}(A)$
, where
$S_{q}(A)$
, where
 $$ \begin{align*}S_{q}^{F}(\boldsymbol{\alpha})=\Big(\sum_{Q\in F}\alpha_{Q}^{q}\chi_{Q}\Big)^{1/q}\end{align*} $$
$$ \begin{align*}S_{q}^{F}(\boldsymbol{\alpha})=\Big(\sum_{Q\in F}\alpha_{Q}^{q}\chi_{Q}\Big)^{1/q}\end{align*} $$
for an arbitrary finite family of cubes
![]() $F\subset {\mathscr D}$
.
$F\subset {\mathscr D}$
.
Write the set
 $\{x \in \mathbb {R}^{n}:S_{q}^{F}(\boldsymbol {\alpha })(x)>\lambda \}$
as the union of its maximal cubes
$\{x \in \mathbb {R}^{n}:S_{q}^{F}(\boldsymbol {\alpha })(x)>\lambda \}$
as the union of its maximal cubes
![]() $Q_{j}\in F$
. Then it suffices to prove that
$Q_{j}\in F$
. Then it suffices to prove that
 $$ \begin{align} \big|\{x\in Q_{j}:S_{q}^{F}(\boldsymbol{\alpha})(x)>2\lambda, M(\boldsymbol{\alpha})(x)\le \varepsilon\lambda\}\big|\le 2e^{-K/\varepsilon^{q}}|Q_{j}|. \end{align} $$
$$ \begin{align} \big|\{x\in Q_{j}:S_{q}^{F}(\boldsymbol{\alpha})(x)>2\lambda, M(\boldsymbol{\alpha})(x)\le \varepsilon\lambda\}\big|\le 2e^{-K/\varepsilon^{q}}|Q_{j}|. \end{align} $$
Denote the set on the left-hand side of (8.4) by
![]() $E_{j}$
and fix
$E_{j}$
and fix
![]() $x\in E_{j}$
. By maximality of
$x\in E_{j}$
. By maximality of
![]() $Q_{j}$
,
$Q_{j}$
,
 $$ \begin{align*} \sum_{R\in F: Q_{j}\subset R}\alpha_{R}^{q}\chi_{R}(x)\le \lambda^{q}, \end{align*} $$
$$ \begin{align*} \sum_{R\in F: Q_{j}\subset R}\alpha_{R}^{q}\chi_{R}(x)\le \lambda^{q}, \end{align*} $$
and hence
 $$ \begin{align*} \sum_{R\in F:R\subseteq Q_{j}}\alpha_{R}^{q}\chi_{R}(x)=S_{q}^{F}(\boldsymbol{\alpha})(x)^{q}-\sum_{R\in F, Q_{j}\subset R}\alpha_{R}^{q}\chi_{R}(x)>(2^{q}-1)\lambda^{q}. \end{align*} $$
$$ \begin{align*} \sum_{R\in F:R\subseteq Q_{j}}\alpha_{R}^{q}\chi_{R}(x)=S_{q}^{F}(\boldsymbol{\alpha})(x)^{q}-\sum_{R\in F, Q_{j}\subset R}\alpha_{R}^{q}\chi_{R}(x)>(2^{q}-1)\lambda^{q}. \end{align*} $$
On the other hand, applying Theorem 8.1 to
 $\{ \alpha _{R}^{q} \}_{R \in \mathcal {D}(Q_{j})}$
, there exists a
$\{ \alpha _{R}^{q} \}_{R \in \mathcal {D}(Q_{j})}$
, there exists a
![]() $\frac {1}{2}$
-sparse family
$\frac {1}{2}$
-sparse family
![]() ${\mathcal F}\subset {\mathcal D}(Q_{j})$
such that for a.e.
${\mathcal F}\subset {\mathcal D}(Q_{j})$
such that for a.e.
![]() $x\in E_{j}$
,
$x\in E_{j}$
,
 $$ \begin{align*} \sum_{R\in F:R\subseteq Q_{j}}\alpha_{R}^{q}\chi_{R}(x)\lesssim \sum_{P\in {\mathcal F}}\alpha_{P}^{q}\chi_{P}(x) \lesssim (\varepsilon\lambda)^{q}\sum_{P\in {\mathcal F}}\chi_{P}(x). \end{align*} $$
$$ \begin{align*} \sum_{R\in F:R\subseteq Q_{j}}\alpha_{R}^{q}\chi_{R}(x)\lesssim \sum_{P\in {\mathcal F}}\alpha_{P}^{q}\chi_{P}(x) \lesssim (\varepsilon\lambda)^{q}\sum_{P\in {\mathcal F}}\chi_{P}(x). \end{align*} $$
So we have
 $\sum _{P\in {\mathcal F}}\chi _{P}(x) \gtrsim \frac {1}{\varepsilon ^{q}}$
and therefore, by Proposition 6.3,
$\sum _{P\in {\mathcal F}}\chi _{P}(x) \gtrsim \frac {1}{\varepsilon ^{q}}$
and therefore, by Proposition 6.3,
 $$ \begin{align*} |E_{j}|\le \Big|\Big\{x\in Q_{j}:\sum_{P\in {\mathcal F}}\chi_{P}(x)\gtrsim \frac{1}{\varepsilon^{q}}\Big\}\Big|\le 2e^{-K/\varepsilon^{q}}|Q_{j}|; \end{align*} $$
$$ \begin{align*} |E_{j}|\le \Big|\Big\{x\in Q_{j}:\sum_{P\in {\mathcal F}}\chi_{P}(x)\gtrsim \frac{1}{\varepsilon^{q}}\Big\}\Big|\le 2e^{-K/\varepsilon^{q}}|Q_{j}|; \end{align*} $$
that is, (8.4) holds and the proof is complete.
Example 8.3. Let
![]() $\mu $
be a nonnegative Borel measure. Given
$\mu $
be a nonnegative Borel measure. Given
![]() $0<\gamma <n$
and
$0<\gamma <n$
and
![]() $q \in (0,\infty )$
, define the nonlinear dyadic potential by
$q \in (0,\infty )$
, define the nonlinear dyadic potential by
 $$ \begin{align*} {\mathcal T}_{q,\gamma}(\mu)&:=\Big(\sum_{Q\in {\mathscr D}}\Big(\frac{\mu(Q)}{|Q|^{1-\gamma/n}}\Big)^{q}\chi_{Q}\Big)^{1/q}.\end{align*} $$
$$ \begin{align*} {\mathcal T}_{q,\gamma}(\mu)&:=\Big(\sum_{Q\in {\mathscr D}}\Big(\frac{\mu(Q)}{|Q|^{1-\gamma/n}}\Big)^{q}\chi_{Q}\Big)^{1/q}.\end{align*} $$
Define also the fractional maximal operator by
 $$ \begin{align*} M_{\gamma}(\mu)&:=\sup_{Q\in {\mathscr D}}\frac{\mu(Q)}{|Q|^{1-\gamma/n}}\chi_{Q}. \end{align*} $$
$$ \begin{align*} M_{\gamma}(\mu)&:=\sup_{Q\in {\mathscr D}}\frac{\mu(Q)}{|Q|^{1-\gamma/n}}\chi_{Q}. \end{align*} $$
In [Reference Honzík and Jaye21], Honzík and Jaye established the following good-
![]() $\lambda $
inequality: there exists
$\lambda $
inequality: there exists
![]() $C_{1},C_{2}>0$
such that for all
$C_{1},C_{2}>0$
such that for all
![]() $\lambda>0$
and
$\lambda>0$
and
![]() $0<\varepsilon <1$
,
$0<\varepsilon <1$
,
 $$ \begin{align} \begin{aligned} \big|\{x \in \mathbb{R}^{n}:{\mathcal T}_{q}(\mu)(x)&>2\lambda, M_{\gamma}(\mu)(x)\le \varepsilon\lambda\}\big| \le C_{1}e^{-C_{2}/\varepsilon^{q}}\big|\{x \in \mathbb{R}^{n}:{\mathcal T}_{q}(\mu)(x)>\lambda\}\big|. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \big|\{x \in \mathbb{R}^{n}:{\mathcal T}_{q}(\mu)(x)&>2\lambda, M_{\gamma}(\mu)(x)\le \varepsilon\lambda\}\big| \le C_{1}e^{-C_{2}/\varepsilon^{q}}\big|\{x \in \mathbb{R}^{n}:{\mathcal T}_{q}(\mu)(x)>\lambda\}\big|. \end{aligned} \end{align} $$
Let us show that this result can be deduced from Corollary 8.2. Indeed, set
 $\alpha _{Q}=\frac {\mu (Q)}{|Q|^{1-\gamma /n}}$
for
$\alpha _{Q}=\frac {\mu (Q)}{|Q|^{1-\gamma /n}}$
for
![]() $Q \in \mathscr {D}$
. It suffices to show that (8.2) holds for
$Q \in \mathscr {D}$
. It suffices to show that (8.2) holds for
![]() $\delta =\min (q,1)$
. Write
$\delta =\min (q,1)$
. Write
![]() ${\mathcal D}(Q)=\cup _{k=0}^{\infty }{\mathcal D}_{k}$
, where
${\mathcal D}(Q)=\cup _{k=0}^{\infty }{\mathcal D}_{k}$
, where
![]() ${\mathcal D}_{k}$
is the kth generation of dyadic subcubes of Q. First, suppose that
${\mathcal D}_{k}$
is the kth generation of dyadic subcubes of Q. First, suppose that
![]() $q\ge 1$
. Then
$q\ge 1$
. Then
![]() $\delta =1$
and we have
$\delta =1$
and we have
 $$ \begin{align*} \sum_{R\in {\mathcal D}(Q)}\alpha_{R}^{\delta}|R|=\sum_{R\in {\mathcal D}(Q)}\mu(R)|R|^{\gamma/n}&=|Q|^{\gamma/n}\sum_{k=0}^{\infty}2^{-k\gamma}\sum_{P\in {\mathcal D}_{k}}\mu(P)\\ &=C_{\gamma}\cdot \mu(Q)|Q|^{\gamma/n}=C_{\gamma}\cdot \alpha_{Q}^{\delta}|Q|. \end{align*} $$
$$ \begin{align*} \sum_{R\in {\mathcal D}(Q)}\alpha_{R}^{\delta}|R|=\sum_{R\in {\mathcal D}(Q)}\mu(R)|R|^{\gamma/n}&=|Q|^{\gamma/n}\sum_{k=0}^{\infty}2^{-k\gamma}\sum_{P\in {\mathcal D}_{k}}\mu(P)\\ &=C_{\gamma}\cdot \mu(Q)|Q|^{\gamma/n}=C_{\gamma}\cdot \alpha_{Q}^{\delta}|Q|. \end{align*} $$
Now suppose that
![]() $q<1$
. Since
$q<1$
. Since
![]() $\#\{Q\in {\mathcal D}_{k}\}=2^{kn}$
, we have by Hölder’s inequality
$\#\{Q\in {\mathcal D}_{k}\}=2^{kn}$
, we have by Hölder’s inequality
 $$ \begin{align*}\sum_{P\in {\mathcal D}_{k}}\mu(P)^{q}\le 2^{nk(1-q)}\mu(Q)^{q}.\end{align*} $$
$$ \begin{align*}\sum_{P\in {\mathcal D}_{k}}\mu(P)^{q}\le 2^{nk(1-q)}\mu(Q)^{q}.\end{align*} $$
Hence, as
![]() $\delta =q$
,
$\delta =q$
,
 $$ \begin{align*} \sum_{R\in {\mathcal D}(Q)}\alpha_{R}^{\delta}|R|&=|Q|^{1-q(1-\gamma/n)}\sum_{k=0}^{\infty}2^{nk((1-\gamma/n)q-1)}\sum_{P\in {\mathcal D}_{k}}\mu(P)^{q}\\ &\le \Big(\frac{\mu(Q)}{|Q|^{1-\gamma/n}}\Big)^{q}|Q|\sum_{k=0}^{\infty}2^{nk((1-\gamma/n)q-1)}2^{nk(1-q)}\\ &= \alpha_{Q}^{q}|Q|\sum_{k=0}^{\infty}2^{-k\gamma q}=C_{\gamma,q}\cdot \alpha_{Q}^{\delta}|Q|. \end{align*} $$
$$ \begin{align*} \sum_{R\in {\mathcal D}(Q)}\alpha_{R}^{\delta}|R|&=|Q|^{1-q(1-\gamma/n)}\sum_{k=0}^{\infty}2^{nk((1-\gamma/n)q-1)}\sum_{P\in {\mathcal D}_{k}}\mu(P)^{q}\\ &\le \Big(\frac{\mu(Q)}{|Q|^{1-\gamma/n}}\Big)^{q}|Q|\sum_{k=0}^{\infty}2^{nk((1-\gamma/n)q-1)}2^{nk(1-q)}\\ &= \alpha_{Q}^{q}|Q|\sum_{k=0}^{\infty}2^{-k\gamma q}=C_{\gamma,q}\cdot \alpha_{Q}^{\delta}|Q|. \end{align*} $$
Acknowledgement
The second author was supported by the Academy of Finland through Grant No. 336323. The third author was partially supported by ANPCyT PICT 2018-2501.
Conflicts of Interest
None.