Article contents
A PROOF OF ANDREWS’ CONJECTURE ON PARTITIONS WITH NO SHORT SEQUENCES
Published online by Cambridge University Press: 30 May 2019
Abstract
Our main result establishes Andrews’ conjecture for the asymptotic of the generating function for the number of integer partitions of  $n$ without
$n$ without 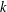 $k$ consecutive parts. The methods we develop are applicable in obtaining asymptotics for stochastic processes that avoid patterns; as a result they yield asymptotics for the number of partitions that avoid patterns.
$k$ consecutive parts. The methods we develop are applicable in obtaining asymptotics for stochastic processes that avoid patterns; as a result they yield asymptotics for the number of partitions that avoid patterns.
Holroyd, Liggett, and Romik, in connection with certain bootstrap percolation models, introduced the study of partitions without 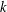 $k$ consecutive parts. Andrews showed that when
$k$ consecutive parts. Andrews showed that when 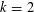 $k=2$, the generating function for these partitions is a mixed-mock modular form and, thus, has modularity properties which can be utilized in the study of this generating function. For
$k=2$, the generating function for these partitions is a mixed-mock modular form and, thus, has modularity properties which can be utilized in the study of this generating function. For 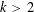 $k>2$, the asymptotic properties of the generating functions have proved more difficult to obtain. Using
$k>2$, the asymptotic properties of the generating functions have proved more difficult to obtain. Using 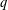 $q$-series identities and the
$q$-series identities and the 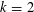 $k=2$ case as evidence, Andrews stated a conjecture for the asymptotic behavior. Extensive computational evidence for the conjecture in the case
$k=2$ case as evidence, Andrews stated a conjecture for the asymptotic behavior. Extensive computational evidence for the conjecture in the case 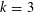 $k=3$ was given by Zagier.
$k=3$ was given by Zagier.
This paper improved upon early approaches to this problem by identifying and overcoming two sources of error. Since the writing of this paper, a more precise asymptotic result was established by Bringmann, Kane, Parry, and Rhoades. That approach uses very different methods.
MSC classification
Information
- Type
- Research Article
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author(s) 2019
References
- 1
- Cited by

