1. Introduction
Over the past two decades there has been a surge of activity in the study of stable, hyperbolic and Lorentzian polynomials. Spectacular applications in several different areas have been given; see [Reference Anari, Liu, Oveis Gharan and Vinzant1, Reference Anari, Liu, Oveis Gharan and Vinzant2, Reference Brändén and Huh7, Reference Marcus, Spielman and Srivastava14, Reference Wagner18] and the references therein. In this article we are interested in the shapes of spaces of such polynomials.
The space of Lorentzian polynomials was studied by Huh and the author in [Reference Brändén and Huh7]; by Gurvits in [Reference Gurvits12], who called it the space of strongly log-concave polynomials; and by Anari et al. in [Reference Anari, Liu, Oveis Gharan and Vinzant2], who called it the space of completely log-concave polynomials. This space contains all volume polynomials of convex bodies and projective varieties, as well as homogeneous stable polynomials with nonnegative coefficients. The theory of Lorentzian polynomials links discrete and continuous notions of convexity. Denote by
![]() $\mathbb {P}\mathrm {L}^{d}_{n}$
the projective space of all Lorentzian degree d polynomials in the variables
$\mathbb {P}\mathrm {L}^{d}_{n}$
the projective space of all Lorentzian degree d polynomials in the variables
![]() $w_{1}, \ldots , w_{n}$
. This remarkable space is stratified by the family of all
$w_{1}, \ldots , w_{n}$
. This remarkable space is stratified by the family of all
![]() $\mathrm {M}$
-convex sets [Reference Murota15] on the discrete simplex. It was proved in [Reference Brändén and Huh7] that the space
$\mathrm {M}$
-convex sets [Reference Murota15] on the discrete simplex. It was proved in [Reference Brändén and Huh7] that the space
![]() $\mathbb {P}\mathrm {L}^{d}_{n}$
is compact and contractible and conjectured that
$\mathbb {P}\mathrm {L}^{d}_{n}$
is compact and contractible and conjectured that
![]() $\mathbb {P}\mathrm {L}^{d}_{n}$
is homeomorphic to a closed Euclidean ball. We prove this conjecture here (Theorem 3.4) by utilising and further developing a powerful connection between the symmetric exclusion process (SEP) and the geometry of polynomials, which was discovered and studied in [Reference Borcea, Brändén and Liggett6]. The proof technique also applies to spaces of real stable polynomials, and we prove that these spaces are homeomorphic to closed Euclidean balls.
$\mathbb {P}\mathrm {L}^{d}_{n}$
is homeomorphic to a closed Euclidean ball. We prove this conjecture here (Theorem 3.4) by utilising and further developing a powerful connection between the symmetric exclusion process (SEP) and the geometry of polynomials, which was discovered and studied in [Reference Borcea, Brändén and Liggett6]. The proof technique also applies to spaces of real stable polynomials, and we prove that these spaces are homeomorphic to closed Euclidean balls.
It was proved in [Reference Borcea, Brändén and Liggett6] and [Reference Brändén and Huh7] that SEP preserves the classes of multiaffine stable and multiaffine Lorentzian polynomials, respectively. In Sections 2 and 4 we study in more detail how SEP acts on multiaffine Lorentzian polynomials. We prove that SEP is a contractive flow (Lemma 2.3) that maps the boundaries of the spaces into their interiors for all positive times (Lemma 2.5). Furthermore, SEP contracts the spaces to a point in the interior. These results are used in Section 3, in conjunction with a construction of Galashin, Karp and Lam [Reference Galashin, Karp and Lam9], to prove that various spaces of Lorentzian polynomials are closed Euclidean balls.
In Section 4 we prove, by similar methods, that projective spaces of real stable polynomials are homeomorphic to closed Euclidean balls. This refines a result of Nuij [Reference Nuij16], who proved that such spaces are contractible.
In the final section we identify topics for further studies.
2. Lorentzian polynomials and the symmetric exclusion process
Let
![]() $\mathrm {H}_{n}^{d}$
denote the linear space of all degree d homogeneous polynomials in
$\mathrm {H}_{n}^{d}$
denote the linear space of all degree d homogeneous polynomials in
![]() $\mathbb {R}[w_{1},\ldots ,w_{n}]$
, adjoining the identically zero polynomial. A polynomial f in
$\mathbb {R}[w_{1},\ldots ,w_{n}]$
, adjoining the identically zero polynomial. A polynomial f in
![]() $\mathrm {H}_{n}^{d}$
, where
$\mathrm {H}_{n}^{d}$
, where
![]() $d\geq 2$
, is strictly Lorentzian if
$d\geq 2$
, is strictly Lorentzian if
-
1. all coefficients of f are positive and
-
2. for any
 $1\leq i_{1}, i_{2}, \ldots , i_{d-2} \leq n$
, the quadratic
$1\leq i_{1}, i_{2}, \ldots , i_{d-2} \leq n$
, the quadratic
 $\partial _{i_{1}} \partial _{i_{2}}\cdots \partial _{i_{d-2}} f$
, where
$\partial _{i_{1}} \partial _{i_{2}}\cdots \partial _{i_{d-2}} f$
, where
 $\partial _{j}= \partial /\partial w_{j}$
, has the Lorentzian signature
$\partial _{j}= \partial /\partial w_{j}$
, has the Lorentzian signature
 $(+,-,-,\ldots ,-)$
.
$(+,-,-,\ldots ,-)$
.
Also, any homogeneous polynomial of degree
![]() $0$
or
$0$
or
![]() $1$
with only positive coefficients is defined to be strictly Lorentzian. Polynomials that are limits in
$1$
with only positive coefficients is defined to be strictly Lorentzian. Polynomials that are limits in
![]() $\mathrm {H}_{n}^{d}$
, in the standard Euclidean topology on the space of coefficients of the polynomials, of strictly Lorentzian polynomials are called Lorentzian.
$\mathrm {H}_{n}^{d}$
, in the standard Euclidean topology on the space of coefficients of the polynomials, of strictly Lorentzian polynomials are called Lorentzian.
Denote by
![]() $\mathrm {L}^{d}_{n}$
the space of Lorentzian polynomials in
$\mathrm {L}^{d}_{n}$
the space of Lorentzian polynomials in
![]() $\mathrm {H}_{n}^{d}$
and by
$\mathrm {H}_{n}^{d}$
and by
![]() $\mathbb {P}\mathrm {L}^{d}_{n}$
the projectivisation of
$\mathbb {P}\mathrm {L}^{d}_{n}$
the projectivisation of
![]() $\mathrm {L}^{d}_{n}$
. Since Lorentzian polynomials have nonnegative coefficients, we may identify
$\mathrm {L}^{d}_{n}$
. Since Lorentzian polynomials have nonnegative coefficients, we may identify
![]() $\mathbb {P}\mathrm {L}^{d}_{n}$
with the space of all polynomials f in
$\mathbb {P}\mathrm {L}^{d}_{n}$
with the space of all polynomials f in
![]() $\mathrm {L}^{d}_{n}$
such that
$\mathrm {L}^{d}_{n}$
such that
![]() $f(\mathbf {1})=1$
, where
$f(\mathbf {1})=1$
, where
![]() $\mathbf {1} =(1,1,\ldots , 1)$
. Let
$\mathbf {1} =(1,1,\ldots , 1)$
. Let
![]() $\mathrm {E}_{n}^{d}$
be the affine Euclidean space of all f in
$\mathrm {E}_{n}^{d}$
be the affine Euclidean space of all f in
![]() $\mathrm {H}_{n}^{d}$
for which
$\mathrm {H}_{n}^{d}$
for which
![]() $f(\mathbf {1})=1$
. Let further
$f(\mathbf {1})=1$
. Let further
![]() $\underline {\mathrm {E}}_{n}^{d}$
and
$\underline {\mathrm {E}}_{n}^{d}$
and
![]() $\underline {\mathrm {H}}_{n}^{d}$
be the spaces of all multiaffine polynomials in
$\underline {\mathrm {H}}_{n}^{d}$
be the spaces of all multiaffine polynomials in
![]() $\mathrm {E}_{n}^{d}$
and
$\mathrm {E}_{n}^{d}$
and
![]() $\mathrm {H}_{n}^{d}$
, respectively; that is, those polynomials in
$\mathrm {H}_{n}^{d}$
, respectively; that is, those polynomials in
![]() $\mathrm {E}_{n}^{d}$
(and
$\mathrm {E}_{n}^{d}$
(and
![]() $\mathrm {H}_{n}^{d}$
) that have degree at most one in each variable. Denote by
$\mathrm {H}_{n}^{d}$
) that have degree at most one in each variable. Denote by
 $\mathbb {P}\underline {\mathrm {L}}_{n}^{d}$
the space of multiaffine polynomials in
$\mathbb {P}\underline {\mathrm {L}}_{n}^{d}$
the space of multiaffine polynomials in
![]() $\mathbb {P}\mathrm {L}^{d}_{n}$
; that is, the space of all Lorentzian polynomials in
$\mathbb {P}\mathrm {L}^{d}_{n}$
; that is, the space of all Lorentzian polynomials in
![]() $\underline {\mathrm {E}}_{n}^{d}$
. We equip
$\underline {\mathrm {E}}_{n}^{d}$
. We equip
![]() $\mathbb {P}\mathrm {L}^{d}_{n}$
and
$\mathbb {P}\mathrm {L}^{d}_{n}$
and
 $\mathbb {P}\underline {\mathrm {L}}_{n}^{d}$
with the standard topology on the affine Euclidean spaces
$\mathbb {P}\underline {\mathrm {L}}_{n}^{d}$
with the standard topology on the affine Euclidean spaces
![]() $\mathrm {E}_{n}^{d}$
and
$\mathrm {E}_{n}^{d}$
and
![]() $\underline {\mathrm {E}}_{n}^{d}$
.
$\underline {\mathrm {E}}_{n}^{d}$
.
For
![]() $0\leq d \leq n$
, let
$0\leq d \leq n$
, let
![]() $[n]=\{1,2,\ldots , n\}$
and
$[n]=\{1,2,\ldots , n\}$
and
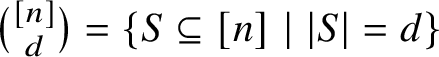 $\binom {[n]} d = \{ S \subseteq [n] \mid |S|=d\}$
. The dth elementary symmetric polynomial in the variables
$\binom {[n]} d = \{ S \subseteq [n] \mid |S|=d\}$
. The dth elementary symmetric polynomial in the variables
![]() $w_{1},\ldots , w_{n}$
is
$w_{1},\ldots , w_{n}$
is
 $$ \begin{align*} e_{d}(\mathbf{w})=e_{d}(w_{1},\ldots, w_{n})= \sum_{S \in \binom {[n]} d } \mathbf{w}^{S}, \ \ \ \ \ \mbox{ where } \mathbf{w}^{S}= \prod_{i \in S}w_{i}. \end{align*} $$
$$ \begin{align*} e_{d}(\mathbf{w})=e_{d}(w_{1},\ldots, w_{n})= \sum_{S \in \binom {[n]} d } \mathbf{w}^{S}, \ \ \ \ \ \mbox{ where } \mathbf{w}^{S}= \prod_{i \in S}w_{i}. \end{align*} $$
Let
 $\mathbb {S}^{n-1}=\{\mathbf {x} \in \mathbb {R}^{n} \mid x_{1}^{2}+\cdots +x_{n}^{2}=1\}$
denote the unit sphere in
$\mathbb {S}^{n-1}=\{\mathbf {x} \in \mathbb {R}^{n} \mid x_{1}^{2}+\cdots +x_{n}^{2}=1\}$
denote the unit sphere in
![]() $\mathbb {R}^{n}$
, and let
$\mathbb {R}^{n}$
, and let
 $\mathbb {S}^{n-2}_{\mathbf {1}}=\{\mathbf {x} \in \mathbb {S}^{n-1} \mid x_{1}+\cdots +x_{n}=0\}$
.
$\mathbb {S}^{n-2}_{\mathbf {1}}=\{\mathbf {x} \in \mathbb {S}^{n-1} \mid x_{1}+\cdots +x_{n}=0\}$
.
Lemma 2.1. Suppose
 $f= \sum _{S \in \binom {[n]} d } a(S) \mathbf {w}^{S}$
is a polynomial in
$f= \sum _{S \in \binom {[n]} d } a(S) \mathbf {w}^{S}$
is a polynomial in
![]() $\mathrm {E}_{n}^{d}$
with nonnegative coefficients
$\mathrm {E}_{n}^{d}$
with nonnegative coefficients
![]() $a(S)$
. Then f is in the interior of
$a(S)$
. Then f is in the interior of
 $\mathbb {P}\underline {\mathrm {L}}^{d}_{n}$
if and only if
$\mathbb {P}\underline {\mathrm {L}}^{d}_{n}$
if and only if
![]() $a(S)>0$
for all
$a(S)>0$
for all
 $S\in \binom {[n]} d$
and one (and then all) of the following three conditions are satisfied:
$S\in \binom {[n]} d$
and one (and then all) of the following three conditions are satisfied:
-
1. for each set
 $S \subset [n]$
of size
$S \subset [n]$
of size
 $d-2$
, the quadratic
$d-2$
, the quadratic
 $\partial ^{S} f=\prod _{j\in S}\partial _{j}f$
, considered as a polynomial in the
$\partial ^{S} f=\prod _{j\in S}\partial _{j}f$
, considered as a polynomial in the
 $n-d+2$
variables
$n-d+2$
variables
 $\{w_{j} \mid j \in [n] \setminus S\}$
, has signature
$\{w_{j} \mid j \in [n] \setminus S\}$
, has signature
 $(+,-,-,\ldots ,-)$
;
$(+,-,-,\ldots ,-)$
; -
2. for each set
 $S \subset [n]$
of size
$S \subset [n]$
of size
 $d-2$
and each
$d-2$
and each
 $\mathbf {y} \in \mathbb {R}^{n-d+2}$
not parallel to
$\mathbf {y} \in \mathbb {R}^{n-d+2}$
not parallel to
 $\mathbf {1}$
, the degree 2 polynomial
$\mathbf {1}$
, the degree 2 polynomial
 $\partial ^{S}f(t\mathbf {1} -\mathbf {y}) $
has two real and distinct zeros;
$\partial ^{S}f(t\mathbf {1} -\mathbf {y}) $
has two real and distinct zeros; -
3. for each set
 $S \subset [n]$
of size
$S \subset [n]$
of size
 $d-2$
and each
$d-2$
and each
 $\mathbf {y} \in \mathbb {S}^{n-d}_{\mathbf {1}}$
, the degree 2 polynomial
$\mathbf {y} \in \mathbb {S}^{n-d}_{\mathbf {1}}$
, the degree 2 polynomial
 $ \partial ^{S}f(t\mathbf {1} -\mathbf {y}) $
has two real and distinct zeros.
$ \partial ^{S}f(t\mathbf {1} -\mathbf {y}) $
has two real and distinct zeros.
Proof. Clearly all coefficients of polynomials in the interior are positive. By, for example, [Reference Brändén and Huh7, Theorem 2.25, Lemma 2.5], the sufficiency (and equivalence) of (1) and (2) follows. Also, (2) and (3) are equivalent by homogeneity.
Suppose (2) fails for some f in the interior of
 $\mathbb {P}\underline {\mathrm {L}}^{d}_{n}$
,
$\mathbb {P}\underline {\mathrm {L}}^{d}_{n}$
,
 $\mathbf {y} \in \mathbb {S}^{n-d}_{\mathbf {1}}$
and
$\mathbf {y} \in \mathbb {S}^{n-d}_{\mathbf {1}}$
and
 $S\in \binom {[n]} {d-2}$
. Let
$S\in \binom {[n]} {d-2}$
. Let
![]() $y_{k}=\min \{y_{i}\}$
and
$y_{k}=\min \{y_{i}\}$
and
![]() $y_{\ell }=\max \{y_{i}\}$
. Since the coefficients of f are positive, it follows that
$y_{\ell }=\max \{y_{i}\}$
. Since the coefficients of f are positive, it follows that
![]() $\partial ^{S}f(t \mathbf {1} -\mathbf {y})=(t-a)^{2}$
, where
$\partial ^{S}f(t \mathbf {1} -\mathbf {y})=(t-a)^{2}$
, where
![]() $y_{k} < a <y_{\ell }$
. Let
$y_{k} < a <y_{\ell }$
. Let
![]() $f_{\epsilon } = (1+\epsilon )f-\epsilon w_{k}w_{\ell }\mathbf {w}^{S}$
. The discriminant of
$f_{\epsilon } = (1+\epsilon )f-\epsilon w_{k}w_{\ell }\mathbf {w}^{S}$
. The discriminant of
![]() $\partial ^{S}f_{\epsilon }(t\mathbf {1} -\mathbf {y})$
is equal to
$\partial ^{S}f_{\epsilon }(t\mathbf {1} -\mathbf {y})$
is equal to
![]() $\epsilon ^{2}(y_{\ell }-y_{k})^{2}-4\epsilon (a-y_{k})(y_{\ell }-a)$
, which is negative for all
$\epsilon ^{2}(y_{\ell }-y_{k})^{2}-4\epsilon (a-y_{k})(y_{\ell }-a)$
, which is negative for all
![]() $\epsilon>0$
sufficiently small. Hence,
$\epsilon>0$
sufficiently small. Hence,
![]() $f_{\epsilon }(t\mathbf {1} -\mathbf {y})$
has non-real zeros for such
$f_{\epsilon }(t\mathbf {1} -\mathbf {y})$
has non-real zeros for such
![]() $\epsilon $
. This contradiction shows that (3) is necessary.
$\epsilon $
. This contradiction shows that (3) is necessary.
Lemma 2.2. Let
![]() $0\leq d \leq n$
be integers. The normalised elementary symmetric polynomial
$0\leq d \leq n$
be integers. The normalised elementary symmetric polynomial
 $e_{d}(\mathbf {w})/\binom n d$
lies in the interior of
$e_{d}(\mathbf {w})/\binom n d$
lies in the interior of
 $\mathbb {P}\underline {\mathrm {L}}^{d}_{n}$
.
$\mathbb {P}\underline {\mathrm {L}}^{d}_{n}$
.
Proof. We may assume
![]() $d\geq 2$
. Let
$d\geq 2$
. Let
![]() $|S|=d-2$
. The Hessian of
$|S|=d-2$
. The Hessian of
![]() $\partial ^{S} e_{d}=e_{2}$
, considered as a polynomial in
$\partial ^{S} e_{d}=e_{2}$
, considered as a polynomial in
![]() $n-d+2$
variables, is
$n-d+2$
variables, is
![]() $\mathbf {1}^{T} \mathbf {1}-I$
, where I is the identity matrix. This matrix has eigenvalues
$\mathbf {1}^{T} \mathbf {1}-I$
, where I is the identity matrix. This matrix has eigenvalues
![]() $-1, -1,\ldots , -1$
and
$-1, -1,\ldots , -1$
and
![]() $n-d+1$
.
$n-d+1$
.
The symmetric exclusion process (SEP) is one of the main models in interacting particle systems [Reference Liggett13]. It models particles moving on a finite or countable set in a continuous way. Particles can only jump to vacant sites, and there can be at most one particle per site; see [Reference Borcea, Brändén and Liggett6, Reference Liggett13]. Here we view SEP as a flow
 $T_{s} : \underline {\mathrm {H}}_{n}^{d} \to \underline {\mathrm {H}}_{n}^{d}$
,
$T_{s} : \underline {\mathrm {H}}_{n}^{d} \to \underline {\mathrm {H}}_{n}^{d}$
,
![]() $s \in \mathbb {R}$
, a family of linear operators indexed by a real parameter (time) satisfying
$s \in \mathbb {R}$
, a family of linear operators indexed by a real parameter (time) satisfying
where
![]() $T_{0}=I$
is the identity operator.
$T_{0}=I$
is the identity operator.
The symmetric group
![]() $\mathfrak {S}_{n}$
acts linearly on
$\mathfrak {S}_{n}$
acts linearly on
 $\underline {\mathrm {H}}_{n}^{d}$
by permuting the variables
$\underline {\mathrm {H}}_{n}^{d}$
by permuting the variables
The flow
 $T_{s} : \underline {\mathrm {H}}_{n}^{d} \to \underline {\mathrm {H}}_{n}^{d}$
,
$T_{s} : \underline {\mathrm {H}}_{n}^{d} \to \underline {\mathrm {H}}_{n}^{d}$
,
![]() $s \in \mathbb {R}$
, is defined by
$s \in \mathbb {R}$
, is defined by
![]() $ T_{s} = e^{-s} e^{s\mathcal {L}}$
, where
$ T_{s} = e^{-s} e^{s\mathcal {L}}$
, where
 $$ \begin{align*}\mathcal{L}= \sum_{\tau} q_{\tau}\tau, \end{align*} $$
$$ \begin{align*}\mathcal{L}= \sum_{\tau} q_{\tau}\tau, \end{align*} $$
where the sum is over all transposition
![]() $\tau $
in
$\tau $
in
![]() $\mathfrak {S}_{n}$
. We require that the numbers
$\mathfrak {S}_{n}$
. We require that the numbers
![]() $q_{\tau }$
are nonnegative and sum to one and that
$q_{\tau }$
are nonnegative and sum to one and that
![]() $\{\tau \mid q_{\tau }>0\}$
generates
$\{\tau \mid q_{\tau }>0\}$
generates
![]() $\mathfrak {S}_{n}$
. Clearly,
$\mathfrak {S}_{n}$
. Clearly,
 $T_{s}: \underline {\mathrm {E}}_{n}^{d}\to \underline {\mathrm {E}}_{n}^{d}$
for all
$T_{s}: \underline {\mathrm {E}}_{n}^{d}\to \underline {\mathrm {E}}_{n}^{d}$
for all
![]() $s \in \mathbb {R}$
, and
$s \in \mathbb {R}$
, and
 $e_{d}(\mathbf {w})/\binom n d$
is an eigenvector/polynomial of
$e_{d}(\mathbf {w})/\binom n d$
is an eigenvector/polynomial of
![]() $\mathcal {L}$
.
$\mathcal {L}$
.
Notice that the matrix corresponding to a transposition
![]() $\tau $
, with respect to the basis
$\tau $
, with respect to the basis
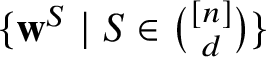 $\{\mathbf {w}^{S} \mid S \in \binom {[n]} d \}$
of
$\{\mathbf {w}^{S} \mid S \in \binom {[n]} d \}$
of
![]() $\underline {\mathrm {H}}_{n}^{d}$
, is symmetric. Hence, so is the matrix corresponding to
$\underline {\mathrm {H}}_{n}^{d}$
, is symmetric. Hence, so is the matrix corresponding to
![]() $\mathcal {L}$
. Thus,
$\mathcal {L}$
. Thus,
![]() $\mathcal {L}$
has an orthogonal basis of eigenvectors
$\mathcal {L}$
has an orthogonal basis of eigenvectors
![]() $f_{0},f_{1}, \ldots , f_{N}$
in
$f_{0},f_{1}, \ldots , f_{N}$
in
![]() $\underline {\mathrm {H}}_{n}^{d}$
, where
$\underline {\mathrm {H}}_{n}^{d}$
, where
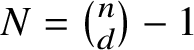 $N= \binom n d-1$
and
$N= \binom n d-1$
and
 $f_{0}(\mathbf {w})= e_{d}(\mathbf {w})/\binom n d$
. Also, by the assumption on
$f_{0}(\mathbf {w})= e_{d}(\mathbf {w})/\binom n d$
. Also, by the assumption on
![]() $\{ \tau \mid q_{\tau }>0\}$
, there exists a positive number m such that for each
$\{ \tau \mid q_{\tau }>0\}$
, there exists a positive number m such that for each
![]() $\epsilon>0$
, all entries of the matrix representing
$\epsilon>0$
, all entries of the matrix representing
![]() $(\mathcal {L}+\epsilon I)^{m}$
are positive. By Perron–Frobenius theory [Reference Berman and Plemmons3, Chapter 1], the eigenvalues of
$(\mathcal {L}+\epsilon I)^{m}$
are positive. By Perron–Frobenius theory [Reference Berman and Plemmons3, Chapter 1], the eigenvalues of
![]() $\mathcal {L}$
satisfy
$\mathcal {L}$
satisfy
Hence, if we write an element f in
![]() $\underline {\mathrm {H}}_{n}^{d}$
as
$\underline {\mathrm {H}}_{n}^{d}$
as
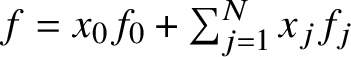 $f= x_{0}f_{0} + \sum _{j=1}^{N} x_{j} f_{j}$
, then
$f= x_{0}f_{0} + \sum _{j=1}^{N} x_{j} f_{j}$
, then
 $$ \begin{align} T_{s}(f)= x_{0}f_{0} + \sum_{j=1}^{N} x_{j} e^{-s(1-\lambda_{j})}f_{j}. \end{align} $$
$$ \begin{align} T_{s}(f)= x_{0}f_{0} + \sum_{j=1}^{N} x_{j} e^{-s(1-\lambda_{j})}f_{j}. \end{align} $$
Consequently,
![]() $T_{s}(f) \to x_{0}f_{0}$
as
$T_{s}(f) \to x_{0}f_{0}$
as
![]() $s \to \infty $
, and since
$s \to \infty $
, and since
![]() $T_{s}(f)(\mathbf {1})=f(\mathbf {1})$
, we have
$T_{s}(f)(\mathbf {1})=f(\mathbf {1})$
, we have
![]() $x_{0}=f(\mathbf {1})$
and
$x_{0}=f(\mathbf {1})$
and
![]() $f_{j}(\mathbf {1})=0$
for all
$f_{j}(\mathbf {1})=0$
for all
![]() $j>0$
.
$j>0$
.
Define a ball of radius r, centred at
![]() $f_{0}$
, by
$f_{0}$
, by
 $$ \begin{align*}B_{r}= \left\{ f_{0} +\sum_{j=1}^{N} x_{j} f_{j} \mid \mathbf{x} \in \mathbb{R}^{N} \mbox{ and } \sum_{j=1}^{N} x_{j}^{2} \leq r^{2}\right\}. \end{align*} $$
$$ \begin{align*}B_{r}= \left\{ f_{0} +\sum_{j=1}^{N} x_{j} f_{j} \mid \mathbf{x} \in \mathbb{R}^{N} \mbox{ and } \sum_{j=1}^{N} x_{j}^{2} \leq r^{2}\right\}. \end{align*} $$
Thus,
![]() $B_{r}$
is a closed Euclidean ball in the affine space
$B_{r}$
is a closed Euclidean ball in the affine space
![]() $\underline {\mathrm {E}}_{n}^{d}$
.
$\underline {\mathrm {E}}_{n}^{d}$
.
Using (2.1), we may read off how
![]() $T_{s}$
deforms the ball
$T_{s}$
deforms the ball
![]() $B_{r}$
.
$B_{r}$
.
Lemma 2.3. If r and s are positive numbers, then
where
![]() $r_{N}(s)= r\exp (-s(1-\lambda _{N}))$
and
$r_{N}(s)= r\exp (-s(1-\lambda _{N}))$
and
![]() $r_{1}(s)=r\exp (-s(1-\lambda _{1}))$
.
$r_{1}(s)=r\exp (-s(1-\lambda _{1}))$
.
The next proposition was essentially proved in [Reference Brändén and Huh7]. For completeness, we provide the remaining details here.
Proposition 2.4. If
![]() $s\geq 0$
, then
$s\geq 0$
, then
 $T_{s} : \underline {\mathrm {L}}^{d}_{n} \to \underline {\mathrm {L}}^{d}_{n}$
.
$T_{s} : \underline {\mathrm {L}}^{d}_{n} \to \underline {\mathrm {L}}^{d}_{n}$
.
Proof. Assume first that
![]() $\mathcal {L}=\tau $
is a transposition. It was proved in [Reference Brändén and Huh7, Corollary 3.9] that any operator of the form
$\mathcal {L}=\tau $
is a transposition. It was proved in [Reference Brändén and Huh7, Corollary 3.9] that any operator of the form
![]() $(1-\theta )I + \theta \tau $
, where
$(1-\theta )I + \theta \tau $
, where
![]() $0\leq \theta \leq 1$
, preserves the Lorentzian property. Since
$0\leq \theta \leq 1$
, preserves the Lorentzian property. Since
 $$ \begin{align*}e^{s\mathcal{L}}= \frac {e^{s}+e^{-s}} 2 I+ \frac {e^{s}-e^{-s}} 2 \tau, \end{align*} $$
$$ \begin{align*}e^{s\mathcal{L}}= \frac {e^{s}+e^{-s}} 2 I+ \frac {e^{s}-e^{-s}} 2 \tau, \end{align*} $$
we deduce
 $e^{s\mathcal {L}} : \underline {\mathrm {L}}^{d}_{n} \to \underline {\mathrm {L}}^{d}_{n}$
for all
$e^{s\mathcal {L}} : \underline {\mathrm {L}}^{d}_{n} \to \underline {\mathrm {L}}^{d}_{n}$
for all
![]() $s\geq 0$
.
$s\geq 0$
.
Suppose
 $\mathcal {L}_{i} : \underline {\mathrm {H}}^{d}_{n} \to \underline {\mathrm {H}}^{d}_{n}$
are linear operators such that
$\mathcal {L}_{i} : \underline {\mathrm {H}}^{d}_{n} \to \underline {\mathrm {H}}^{d}_{n}$
are linear operators such that
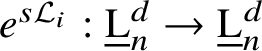 $e^{s\mathcal {L}_{i}} : \underline {\mathrm {L}}^{d}_{n} \to \underline {\mathrm {L}}^{d}_{n}$
for
$e^{s\mathcal {L}_{i}} : \underline {\mathrm {L}}^{d}_{n} \to \underline {\mathrm {L}}^{d}_{n}$
for
![]() $i=1,2$
and all
$i=1,2$
and all
![]() $s\geq 0$
. By the Trotter product formula [Reference Ethier and Kurtz8, page 33],
$s\geq 0$
. By the Trotter product formula [Reference Ethier and Kurtz8, page 33],
 $$ \begin{align*}e^{s(\mathcal{L}_{1}+\mathcal{L}_{2})}= \lim_{k\to \infty} \left( e^{(s/k)\mathcal{L}_{1}} \circ e^{(s/k)\mathcal{L}_{2}}\right)^{k}. \end{align*} $$
$$ \begin{align*}e^{s(\mathcal{L}_{1}+\mathcal{L}_{2})}= \lim_{k\to \infty} \left( e^{(s/k)\mathcal{L}_{1}} \circ e^{(s/k)\mathcal{L}_{2}}\right)^{k}. \end{align*} $$
Hence,
 $e^{s(\mathcal {L}_{1}+\mathcal {L}_{2})} : \underline {\mathrm {L}}^{d}_{n} \to \underline {\mathrm {L}}^{d}_{n}$
, for all
$e^{s(\mathcal {L}_{1}+\mathcal {L}_{2})} : \underline {\mathrm {L}}^{d}_{n} \to \underline {\mathrm {L}}^{d}_{n}$
, for all
![]() $s\geq 0$
, since
$s\geq 0$
, since
![]() $\underline {\mathrm {L}}^{d}_{n}$
is closed. Iterating this proves the proposition.
$\underline {\mathrm {L}}^{d}_{n}$
is closed. Iterating this proves the proposition.
Lemma 2.5. If
 $f \in \mathbb {P}\underline {\mathrm {L}}^{d}_{n}$
and
$f \in \mathbb {P}\underline {\mathrm {L}}^{d}_{n}$
and
![]() $s>0$
, then
$s>0$
, then
![]() $T_{s}(f)$
lies in the interior of
$T_{s}(f)$
lies in the interior of
 $\mathbb {P}\underline {\mathrm {L}}^{d}_{n}$
.
$\mathbb {P}\underline {\mathrm {L}}^{d}_{n}$
.
Proof. By the open mapping theorem and Proposition 2.4,
![]() $T_{s}$
maps the interior of
$T_{s}$
maps the interior of
![]() $\underline {\mathrm {L}}^{d}_{n}$
to itself for each
$\underline {\mathrm {L}}^{d}_{n}$
to itself for each
![]() $s\geq 0$
. Hence, it suffices to prove that if f is in
$s\geq 0$
. Hence, it suffices to prove that if f is in
 $\mathbb {P}\underline {\mathrm {L}}^{d}_{n}$
, then
$\mathbb {P}\underline {\mathrm {L}}^{d}_{n}$
, then
![]() $T_{s}(f)$
lies in the interior of
$T_{s}(f)$
lies in the interior of
 $\mathbb {P}\underline {\mathrm {L}}^{d}_{n}$
for all
$\mathbb {P}\underline {\mathrm {L}}^{d}_{n}$
for all
![]() $s>0$
sufficiently small.
$s>0$
sufficiently small.
All coefficients of
![]() $T_{s}(f)$
are positive for all
$T_{s}(f)$
are positive for all
![]() $s>0$
and
$s>0$
and
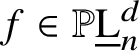 $f \in \mathbb {P}\underline {\mathrm {L}}^{d}_{n}$
. Let
$f \in \mathbb {P}\underline {\mathrm {L}}^{d}_{n}$
. Let
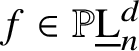 $f \in \mathbb {P}\underline {\mathrm {L}}^{d}_{n}$
and suppose
$f \in \mathbb {P}\underline {\mathrm {L}}^{d}_{n}$
and suppose
![]() $S \subset [n]$
has size
$S \subset [n]$
has size
![]() $d-2$
and that
$d-2$
and that
 $\mathbf {y} \in \mathbb {S}^{n-d}_{\mathbf {1}}$
. Denote by
$\mathbf {y} \in \mathbb {S}^{n-d}_{\mathbf {1}}$
. Denote by
![]() $\Delta _{S}(\mathbf {y};s)$
the discriminant of the degree
$\Delta _{S}(\mathbf {y};s)$
the discriminant of the degree
![]() $2$
polynomial
$2$
polynomial
From (2.1) it follows that
![]() $\Delta _{S}(\mathbf {y};s)$
defines an entire function in the (complex) variable s. Hence, either there is a positive number
$\Delta _{S}(\mathbf {y};s)$
defines an entire function in the (complex) variable s. Hence, either there is a positive number
![]() $\delta (\mathbf {y})$
for which
$\delta (\mathbf {y})$
for which
![]() $\Delta _{S}(\mathbf {y};s) \neq 0$
whenever
$\Delta _{S}(\mathbf {y};s) \neq 0$
whenever
![]() $0<|s|<\delta (\mathbf {y})$
or
$0<|s|<\delta (\mathbf {y})$
or
![]() $\Delta _{f}\!(\mathbf {y};s)$
is identically zero. The latter cannot happen since then, by letting
$\Delta _{f}\!(\mathbf {y};s)$
is identically zero. The latter cannot happen since then, by letting
![]() $s \to \infty $
, it follows that the discriminant of the polynomial
$s \to \infty $
, it follows that the discriminant of the polynomial
![]() $t \mapsto e_{2}(t\mathbf {1} -\mathbf {y})$
is equal to zero, which contradicts the fact that
$t \mapsto e_{2}(t\mathbf {1} -\mathbf {y})$
is equal to zero, which contradicts the fact that
![]() $e_{2}(\mathbf {w})$
is in the interior of
$e_{2}(\mathbf {w})$
is in the interior of
![]() $\mathbb {P}\mathrm {L}^{2}_{n}$
. By compactness (of
$\mathbb {P}\mathrm {L}^{2}_{n}$
. By compactness (of
 $\mathbb {S}^{n-d}_{\mathbf {1}}$
) and Hurwitz’s theorem on the continuity of zeros, it follows that there is a uniform
$\mathbb {S}^{n-d}_{\mathbf {1}}$
) and Hurwitz’s theorem on the continuity of zeros, it follows that there is a uniform
![]() $\delta>0$
such that
$\delta>0$
such that
![]() $\Delta _{S}(\mathbf {y};s) \neq 0$
whenever
$\Delta _{S}(\mathbf {y};s) \neq 0$
whenever
![]() $0<|s|<\delta $
and
$0<|s|<\delta $
and
 $\mathbf {y} \in \mathbb {S}^{n-d}_{\mathbf {1}}$
and
$\mathbf {y} \in \mathbb {S}^{n-d}_{\mathbf {1}}$
and
![]() $S \subset [n]$
has size
$S \subset [n]$
has size
![]() $d-2$
. Hence,
$d-2$
. Hence,
![]() $T_{s}(f)$
is in the interior of
$T_{s}(f)$
is in the interior of
![]() $\mathbb {P}\mathrm {L}^{d}_{n}$
for all
$\mathbb {P}\mathrm {L}^{d}_{n}$
for all
![]() $0<s<\delta $
.
$0<s<\delta $
.
3. Balls of Lorentzian polynomials
Let
 $\mathcal {A}= \{A_{j}\}_{j=1}^{m}$
be a partition of the set of variables
$\mathcal {A}= \{A_{j}\}_{j=1}^{m}$
be a partition of the set of variables
![]() $\{w_{1},\ldots , w_{n}\}$
; that is, a collection of pairwise disjoint and nonempty sets such that
$\{w_{1},\ldots , w_{n}\}$
; that is, a collection of pairwise disjoint and nonempty sets such that
Let further
 $\underline {\mathrm {E}}_{\mathcal {A}}^{d}$
be the space of all polynomials in
$\underline {\mathrm {E}}_{\mathcal {A}}^{d}$
be the space of all polynomials in
![]() $\underline {\mathrm {E}}_{n}^{d}$
that are symmetric in the variables in
$\underline {\mathrm {E}}_{n}^{d}$
that are symmetric in the variables in
![]() $A_{j}$
for each
$A_{j}$
for each
![]() $j \in [m]$
.
$j \in [m]$
.
Consider the symmetric exclusion process,
![]() $T_{s}$
, with rates
$T_{s}$
, with rates
![]() $q_{\tau }=1/\binom n 2$
for all transpositions
$q_{\tau }=1/\binom n 2$
for all transpositions
![]() $\tau $
in
$\tau $
in
![]() $\mathfrak {S}_{n}$
. Then
$\mathfrak {S}_{n}$
. Then
![]() $\tau \mathcal {L} \tau = \mathcal {L}$
for all transpositions
$\tau \mathcal {L} \tau = \mathcal {L}$
for all transpositions
![]() $\tau $
, so that
$\tau $
, so that
 $T_{s} : \underline {\mathrm {E}}_{\mathcal {A}}^{d} \to \underline {\mathrm {E}}_{\mathcal {A}}^{d}$
for all
$T_{s} : \underline {\mathrm {E}}_{\mathcal {A}}^{d} \to \underline {\mathrm {E}}_{\mathcal {A}}^{d}$
for all
![]() $s \in \mathbb {R}$
. Let
$s \in \mathbb {R}$
. Let
 $\mathbb {P}\underline {\mathrm {L}}_{\mathcal {A}}^{d}= \mathbb {P}\underline {\mathrm {L}}_{n}^{d} \cap \underline {\mathrm {E}}_{\mathcal {A}}^{d}$
.
$\mathbb {P}\underline {\mathrm {L}}_{\mathcal {A}}^{d}= \mathbb {P}\underline {\mathrm {L}}_{n}^{d} \cap \underline {\mathrm {E}}_{\mathcal {A}}^{d}$
.
We are now in a position to prove our main results for Lorentzian polynomials. The final tool needed is a general construction in [Reference Galashin, Karp and Lam9]. Explicit homeomorphisms may be extracted from the proof of [Reference Galashin, Karp and Lam9, Lemma 2.3].
Theorem 3.1. Let
![]() $\mathcal {A}$
be a partition of
$\mathcal {A}$
be a partition of
![]() $\{w_{1},\ldots , w_{n}\}$
. The space
$\{w_{1},\ldots , w_{n}\}$
. The space
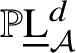 $\mathbb {P}\underline {\mathrm {L}}^{d}_{\mathcal {A}}$
is homeomorphic to a closed Euclidean ball.
$\mathbb {P}\underline {\mathrm {L}}^{d}_{\mathcal {A}}$
is homeomorphic to a closed Euclidean ball.
Proof. Notice that
 $\underline {\mathrm {E}}_{\mathcal {A}}^{d}$
is the intersection of
$\underline {\mathrm {E}}_{\mathcal {A}}^{d}$
is the intersection of
![]() $\underline {\mathrm {E}}_{n}^{d}$
with an affine space,
$\underline {\mathrm {E}}_{n}^{d}$
with an affine space,
![]() $f_{0}+U$
, where U is a linear subspace of
$f_{0}+U$
, where U is a linear subspace of
![]() $\operatorname {\mathrm {span}}\{f_{1},\ldots , f_{N}\}$
. We identify the affine linear space
$\operatorname {\mathrm {span}}\{f_{1},\ldots , f_{N}\}$
. We identify the affine linear space
 $\underline {\mathrm {E}}_{\mathcal {A}}^{d}$
with
$\underline {\mathrm {E}}_{\mathcal {A}}^{d}$
with
![]() $\mathbb {R}^{M}$
, where
$\mathbb {R}^{M}$
, where
![]() $M=\dim (U)$
, equipped with the Euclidean norm, inherited by
$M=\dim (U)$
, equipped with the Euclidean norm, inherited by
![]() $\operatorname {\mathrm {span}}\{f_{1},\ldots , f_{N}\}$
,
$\operatorname {\mathrm {span}}\{f_{1},\ldots , f_{N}\}$
,
 $$ \begin{align*}\| f \| = \sqrt{\sum_{i=1}^{N} x_{i}^{2}}, \ \ \ \ \ \mbox{ if } f = \sum_{i=1}^{N} x_{i}f_{i}. \end{align*} $$
$$ \begin{align*}\| f \| = \sqrt{\sum_{i=1}^{N} x_{i}^{2}}, \ \ \ \ \ \mbox{ if } f = \sum_{i=1}^{N} x_{i}f_{i}. \end{align*} $$
Consider the map
![]() $F : \mathbb {R} \times \mathbb {R}^{M} \to \mathbb {R}^{M}$
defined by
$F : \mathbb {R} \times \mathbb {R}^{M} \to \mathbb {R}^{M}$
defined by
Then
-
1. the map F is continuous, by, for example, the explicit form (2.1),
-
2.
 $F(0,f)=f$
and
$F(0,f)=f$
and
 $F(s_{1}+s_{2}, f)=F(s_{1}, F(s_{2},f))$
, for all
$F(s_{1}+s_{2}, f)=F(s_{1}, F(s_{2},f))$
, for all
 $f \in \mathbb {R}^{M}$
and
$f \in \mathbb {R}^{M}$
and
 $s_{1}, s_{2} \in \mathbb {R}$
,
$s_{1}, s_{2} \in \mathbb {R}$
, -
3.
 $\|F(s,f)\| <\|f\|$
, for all
$\|F(s,f)\| <\|f\|$
, for all
 $f \neq 0$
and
$f \neq 0$
and
 $s>0$
, by Lemma 2.3.
$s>0$
, by Lemma 2.3.
Thus, F is a contractive flow, as defined in [Reference Galashin, Karp and Lam9]. By Lemma 2.5,
 $$ \begin{align*}F(s, \mathbb{P}\underline{\mathrm{L}}^{d}_{\mathcal{A}}) \subset \mathrm{int}(\mathbb{P}\underline{\mathrm{L}}^{d}_{\mathcal{A}}) \ \ \text{for all} s>0, \end{align*} $$
$$ \begin{align*}F(s, \mathbb{P}\underline{\mathrm{L}}^{d}_{\mathcal{A}}) \subset \mathrm{int}(\mathbb{P}\underline{\mathrm{L}}^{d}_{\mathcal{A}}) \ \ \text{for all} s>0, \end{align*} $$
where
![]() $\mathrm {int}$
denotes the interior. The theorem now follows from [Reference Galashin, Karp and Lam9, Lemma 2.3] and its proof.
$\mathrm {int}$
denotes the interior. The theorem now follows from [Reference Galashin, Karp and Lam9, Lemma 2.3] and its proof.
The case of Theorem 3.1 when
![]() $\mathcal {A}$
is the partition
$\mathcal {A}$
is the partition
![]() $\{w_{1}\}, \{w_{2}\}, \ldots , \{w_{n}\}$
, yields the following theorem.
$\{w_{1}\}, \{w_{2}\}, \ldots , \{w_{n}\}$
, yields the following theorem.
Theorem 3.2. The space
 $\mathbb {P}\underline {\mathrm {L}}^{d}_{n}$
is homeomorphic to a closed Euclidean ball.
$\mathbb {P}\underline {\mathrm {L}}^{d}_{n}$
is homeomorphic to a closed Euclidean ball.
Let
![]() $\kappa =(\kappa _{1}, \ldots , \kappa _{n})$
be a vector of positive integers. Define
$\kappa =(\kappa _{1}, \ldots , \kappa _{n})$
be a vector of positive integers. Define
![]() $\mathrm {E}^{d}_{\kappa }$
to be the space of all polynomials f in
$\mathrm {E}^{d}_{\kappa }$
to be the space of all polynomials f in
![]() $\mathrm {E}^{d}_{n}$
for which the degree of f in the variable
$\mathrm {E}^{d}_{n}$
for which the degree of f in the variable
![]() $w_{i}$
is at most
$w_{i}$
is at most
![]() $\kappa _{i}$
, for each
$\kappa _{i}$
, for each
![]() $1\leq i \leq n$
. Also, let
$1\leq i \leq n$
. Also, let
![]() $\mathbb {P}\mathrm {L}^{d}_{\kappa }=\mathrm {E}^{d}_{\kappa } \cap \mathbb {P}\mathrm {L}^{d}_{n}$
.
$\mathbb {P}\mathrm {L}^{d}_{\kappa }=\mathrm {E}^{d}_{\kappa } \cap \mathbb {P}\mathrm {L}^{d}_{n}$
.
Theorem 3.3. The space
![]() $\mathbb {P}\mathrm {L}^{d}_{\kappa }$
is homeomorphic to a closed Euclidean ball.
$\mathbb {P}\mathrm {L}^{d}_{\kappa }$
is homeomorphic to a closed Euclidean ball.
Proof. Consider the variables
![]() $w_{ij}$
,
$w_{ij}$
,
![]() $1\leq i \leq n$
and
$1\leq i \leq n$
and
![]() $1\leq j \leq \kappa _{j}$
, and let
$1\leq j \leq \kappa _{j}$
, and let
![]() $\mathcal {A}=\{A_{1}, \ldots , A_{n}\}$
be the partition of
$\mathcal {A}=\{A_{1}, \ldots , A_{n}\}$
be the partition of
![]() $\{w_{ij}\}$
given by
$\{w_{ij}\}$
given by
![]() $A_{i}=\{ w_{ij} \mid 1\leq j \leq \kappa _{i}\}$
for
$A_{i}=\{ w_{ij} \mid 1\leq j \leq \kappa _{i}\}$
for
![]() $1 \leq i \leq n$
.
$1 \leq i \leq n$
.
The polarisation operator
 $\Pi ^{\uparrow } : \mathrm {E}^{d}_{\kappa } \rightarrow \underline {\mathrm {E}}^{d}_{\mathcal {A}}$
is defined as follows. Let
$\Pi ^{\uparrow } : \mathrm {E}^{d}_{\kappa } \rightarrow \underline {\mathrm {E}}^{d}_{\mathcal {A}}$
is defined as follows. Let
![]() $f \in \mathrm {E}^{d}_{\kappa }$
. For all
$f \in \mathrm {E}^{d}_{\kappa }$
. For all
![]() $i \in [n]$
and each monomial
$i \in [n]$
and each monomial
![]() $w_{1}^{\alpha _{1}} \cdots w_{n}^{\alpha _{n}}$
in the expansion of f, replace
$w_{1}^{\alpha _{1}} \cdots w_{n}^{\alpha _{n}}$
in the expansion of f, replace
![]() $w_{i}^{\alpha _{i}}$
with
$w_{i}^{\alpha _{i}}$
with
 $$ \begin{align*}e_{\alpha_{i}}(w_{i1},\ldots, w_{i\kappa_{i}} )/ \binom {\kappa_{i}} {\alpha_{i}}. \end{align*} $$
$$ \begin{align*}e_{\alpha_{i}}(w_{i1},\ldots, w_{i\kappa_{i}} )/ \binom {\kappa_{i}} {\alpha_{i}}. \end{align*} $$
The polarisation operator is a linear isomorphism with inverse
![]() $\Pi ^{\downarrow }$
defined by the change of variables
$\Pi ^{\downarrow }$
defined by the change of variables
![]() $w_{ij} \to w_{i}$
. Also
$w_{ij} \to w_{i}$
. Also
![]() $\Pi ^{\uparrow }$
and
$\Pi ^{\uparrow }$
and
![]() $\Pi ^{\downarrow }$
preserve the Lorentzian property [Reference Brändén and Huh7, Proposition 3.1]. Hence,
$\Pi ^{\downarrow }$
preserve the Lorentzian property [Reference Brändén and Huh7, Proposition 3.1]. Hence,
![]() $\Pi ^{\uparrow }$
defines a homeomorphism between
$\Pi ^{\uparrow }$
defines a homeomorphism between
![]() $\mathbb {P}\mathrm {L}^{d}_{\kappa }$
and
$\mathbb {P}\mathrm {L}^{d}_{\kappa }$
and
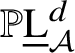 $\mathbb {P}\underline {\mathrm {L}}_{\mathcal {A}}^{d}$
. The theorem now follows from Theorem 3.1.
$\mathbb {P}\underline {\mathrm {L}}_{\mathcal {A}}^{d}$
. The theorem now follows from Theorem 3.1.
By choosing
![]() $\kappa =(d,d,\ldots , d)$
in Theorem 3.3, we have arrived at a proof of [Reference Brändén and Huh7, Conjecture 2.29].
$\kappa =(d,d,\ldots , d)$
in Theorem 3.3, we have arrived at a proof of [Reference Brändén and Huh7, Conjecture 2.29].
Theorem 3.4. The space
![]() $\mathbb {P}\mathrm {L}^{d}_{n}$
is homeomorphic to a closed Euclidean ball.
$\mathbb {P}\mathrm {L}^{d}_{n}$
is homeomorphic to a closed Euclidean ball.
4. Balls of real stable polynomials
A polynomial f in
![]() $\mathbb {R}[w_{1}, \ldots , w_{n}]$
is real stable if
$\mathbb {R}[w_{1}, \ldots , w_{n}]$
is real stable if
![]() $f(\mathbf {w}) \neq 0$
whenever
$f(\mathbf {w}) \neq 0$
whenever
![]() $\mathrm {Im}(w_{j})>0$
for all
$\mathrm {Im}(w_{j})>0$
for all
![]() $j \in [n]$
; see [Reference Borcea and Brändén4, Reference Borcea and Brändén5, Reference Wagner18]. Homogeneous real stable polynomials with nonnegative coefficients are Lorentzian; see [Reference Brändén and Huh7, Proposition 2.2]. Let
$j \in [n]$
; see [Reference Borcea and Brändén4, Reference Borcea and Brändén5, Reference Wagner18]. Homogeneous real stable polynomials with nonnegative coefficients are Lorentzian; see [Reference Brändén and Huh7, Proposition 2.2]. Let
![]() $\mathrm {S}^{d}_{n}$
be the space of degree d homogeneous and real stable polynomials f in
$\mathrm {S}^{d}_{n}$
be the space of degree d homogeneous and real stable polynomials f in
![]() $ \mathbb {R}[w_{1}, \ldots , w_{n}]$
with nonnegative coefficients. Let further
$ \mathbb {R}[w_{1}, \ldots , w_{n}]$
with nonnegative coefficients. Let further
![]() $\mathbb {P}\mathrm {S}^{d}_{n}$
be the set of all
$\mathbb {P}\mathrm {S}^{d}_{n}$
be the set of all
![]() $f \in \mathrm {S}^{d}_{n}$
for which
$f \in \mathrm {S}^{d}_{n}$
for which
![]() $f(\mathbf {1})=1$
. It follows from [Reference Borcea, Brändén and Liggett6, Theorem 4.5] that a polynomial
$f(\mathbf {1})=1$
. It follows from [Reference Borcea, Brändén and Liggett6, Theorem 4.5] that a polynomial
![]() $f \in \mathrm {H}^{d}_{n}$
with nonnegative coefficients is real stable if and only if for each
$f \in \mathrm {H}^{d}_{n}$
with nonnegative coefficients is real stable if and only if for each
![]() $\mathbf {y} \in \mathbb {R}^{n}$
, the polynomial
$\mathbf {y} \in \mathbb {R}^{n}$
, the polynomial
has only real zeros. Notice that by homogeneity this condition is equivalent to the condition: for each
 $\mathbf {y} \in \mathbb {S}^{n-2}_{\mathbf {1}}$
, the polynomial
$\mathbf {y} \in \mathbb {S}^{n-2}_{\mathbf {1}}$
, the polynomial
![]() $ t \mapsto f(t\mathbf {1} -\mathbf {y}) $
has only real zeros. By compactness it follows that
$ t \mapsto f(t\mathbf {1} -\mathbf {y}) $
has only real zeros. By compactness it follows that
![]() $f \in \mathrm {H}^{d}_{n}$
is in the interior of
$f \in \mathrm {H}^{d}_{n}$
is in the interior of
![]() $\mathrm {S}^{d}_{n}$
if and only if all coefficients of f are positive, and for each
$\mathrm {S}^{d}_{n}$
if and only if all coefficients of f are positive, and for each
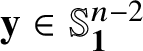 $\mathbf {y} \in \mathbb {S}^{n-2}_{\mathbf {1}}$
, the polynomial
$\mathbf {y} \in \mathbb {S}^{n-2}_{\mathbf {1}}$
, the polynomial
![]() $ t \mapsto f(t\mathbf {1} -\mathbf {y}) $
has only real and distinct zeros.
$ t \mapsto f(t\mathbf {1} -\mathbf {y}) $
has only real and distinct zeros.
Lemma 4.1. Let
![]() $0\leq d \leq n$
be integers, and let
$0\leq d \leq n$
be integers, and let
![]() $\mathbf {y} \in \mathbb {R}^{n}$
be such that at most
$\mathbf {y} \in \mathbb {R}^{n}$
be such that at most
![]() $n-d+1$
of the coordinates agree. Then the zeros of
$n-d+1$
of the coordinates agree. Then the zeros of
![]() $e_{d}(t\mathbf {1} -\mathbf {y})$
are real and distinct.
$e_{d}(t\mathbf {1} -\mathbf {y})$
are real and distinct.
Proof. For
![]() $\mathbf {y} \in \mathbb {R}^{n}$
, let
$\mathbf {y} \in \mathbb {R}^{n}$
, let
![]() $p(t)= \prod _{i=1}^{n} (t-y_{i})$
. Notice that
$p(t)= \prod _{i=1}^{n} (t-y_{i})$
. Notice that
the
![]() $(n-d)$
th derivative of
$(n-d)$
th derivative of
![]() $p(t)$
. Hence, all zeros of
$p(t)$
. Hence, all zeros of
![]() $e_{d}(t\mathbf {1} -\mathbf {y})$
are real. Moreover, if
$e_{d}(t\mathbf {1} -\mathbf {y})$
are real. Moreover, if
![]() $\alpha $
is a zero of
$\alpha $
is a zero of
![]() $e_{d}(t\mathbf {1} -\mathbf {y})$
of multiplicity
$e_{d}(t\mathbf {1} -\mathbf {y})$
of multiplicity
![]() $k \geq 2$
, then
$k \geq 2$
, then
![]() $\alpha $
is a zero of p of multiplicity
$\alpha $
is a zero of p of multiplicity
![]() $k+(n-d)$
. The lemma follows.
$k+(n-d)$
. The lemma follows.
For
![]() $1\leq d \leq n$
, let
$1\leq d \leq n$
, let
![]() $f_{n}^{d}(w_{1},\ldots , w_{n})$
be the polynomial obtained from
$f_{n}^{d}(w_{1},\ldots , w_{n})$
be the polynomial obtained from
 $e_{d}(w_{11}, w_{12}, \ldots , w_{nd})/\binom {nd} d$
by the change of variables
$e_{d}(w_{11}, w_{12}, \ldots , w_{nd})/\binom {nd} d$
by the change of variables
![]() $w_{ij} \to w_{i}$
for all
$w_{ij} \to w_{i}$
for all
![]() $1 \leq i \leq n$
and
$1 \leq i \leq n$
and
![]() $1 \leq j \leq d$
.
$1 \leq j \leq d$
.
Lemma 4.2. The polynomial
![]() $f_{n}^{d}(\mathbf {w})$
lies in the interior of
$f_{n}^{d}(\mathbf {w})$
lies in the interior of
![]() $\mathbb {P}\mathrm {S}^{d}_{n}$
.
$\mathbb {P}\mathrm {S}^{d}_{n}$
.
Proof. All coefficients of
![]() $f_{n}^{d}(\mathbf {w})$
are positive. We need to prove that the zeros of
$f_{n}^{d}(\mathbf {w})$
are positive. We need to prove that the zeros of
![]() $f_{n}^{d}(t\mathbf {1} -\mathbf {y})$
are real and distinct whenever
$f_{n}^{d}(t\mathbf {1} -\mathbf {y})$
are real and distinct whenever
![]() $\mathbf {y} \in \mathbb {R}^{n}$
is not parallel to
$\mathbf {y} \in \mathbb {R}^{n}$
is not parallel to
![]() $\mathbf {1}$
. This follows from Lemma 4.1, since
$\mathbf {1}$
. This follows from Lemma 4.1, since
 $$ \begin{align*}f_{n}^{d}(t\mathbf{1} -\mathbf{y})= e_{d}(t\mathbf{1} -\widetilde{\mathbf{y}})/\binom {nd} d, \mbox{ where } \widetilde{\mathbf{y}}=(y_{1},\ldots, y_{1}, \ldots, y_{n}, \ldots, y_{n}).\\[-42pt] \end{align*} $$
$$ \begin{align*}f_{n}^{d}(t\mathbf{1} -\mathbf{y})= e_{d}(t\mathbf{1} -\widetilde{\mathbf{y}})/\binom {nd} d, \mbox{ where } \widetilde{\mathbf{y}}=(y_{1},\ldots, y_{1}, \ldots, y_{n}, \ldots, y_{n}).\\[-42pt] \end{align*} $$
Theorem 4.3. The space
![]() $\mathbb {P}\mathrm {S}^{d}_{n}$
is homeomorphic to a closed Euclidean ball.
$\mathbb {P}\mathrm {S}^{d}_{n}$
is homeomorphic to a closed Euclidean ball.
Proof. The proof is a modification of the proof of Theorem 3.1.
It was proved in [Reference Borcea, Brändén and Liggett6, Proposition 5.1] that SEP preserves stability on multiaffine polynomials. Also, in [Reference Borcea and Brändén4, Proposition 3.4] it was proved that the polarisation operator
![]() $\Pi ^{\uparrow }$
preserves stability. For
$\Pi ^{\uparrow }$
preserves stability. For
![]() $s \in \mathbb {R}$
, define
$s \in \mathbb {R}$
, define
 $\widehat {T}_{s} : \mathrm {E}_{n}^{d} \to \mathrm {E}_{n}^{d}$
by
$\widehat {T}_{s} : \mathrm {E}_{n}^{d} \to \mathrm {E}_{n}^{d}$
by
![]() $\widehat {T}_{s}= \Pi ^{\downarrow } \circ T_{s} \circ \Pi ^{\uparrow }$
, where
$\widehat {T}_{s}= \Pi ^{\downarrow } \circ T_{s} \circ \Pi ^{\uparrow }$
, where
![]() $T_{s}$
is the SEP on
$T_{s}$
is the SEP on
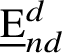 $\underline {\mathrm {E}}_{nd}^{d}$
, with rates
$\underline {\mathrm {E}}_{nd}^{d}$
, with rates
 $q_{\tau } = 1/ \binom {nd} 2$
for all transpositions
$q_{\tau } = 1/ \binom {nd} 2$
for all transpositions
![]() $\tau $
. By the discussion in Section 3, it follows that
$\tau $
. By the discussion in Section 3, it follows that
![]() $\widehat {T}_{s}$
is a contractive flow, which contracts the space to the point
$\widehat {T}_{s}$
is a contractive flow, which contracts the space to the point
![]() $f_{n}^{d}(\mathbf {w})$
in its interior (Lemma 4.2). To finish the proof, it remains to prove that for each fixed
$f_{n}^{d}(\mathbf {w})$
in its interior (Lemma 4.2). To finish the proof, it remains to prove that for each fixed
![]() $f \in \mathbb {P}\mathrm {S}^{d}_{n}$
, there is a
$f \in \mathbb {P}\mathrm {S}^{d}_{n}$
, there is a
![]() $\delta>0$
such that
$\delta>0$
such that
![]() $\widehat {T}_{s}(f)$
is in the interior of
$\widehat {T}_{s}(f)$
is in the interior of
![]() $\mathbb {P}\mathrm {S}^{d}_{n}$
for all
$\mathbb {P}\mathrm {S}^{d}_{n}$
for all
![]() $0<s<\delta $
.
$0<s<\delta $
.
Let
![]() $f \in \mathbb {P}\mathrm {S}^{d}_{n}$
and
$f \in \mathbb {P}\mathrm {S}^{d}_{n}$
and
 $\mathbf {y} \in \mathbb {S}^{n-2}_{\mathbf {1}}$
. Denote by
$\mathbf {y} \in \mathbb {S}^{n-2}_{\mathbf {1}}$
. Denote by
![]() $\Delta _{f}\!(\mathbf {y};s)$
the discriminant of the polynomial
$\Delta _{f}\!(\mathbf {y};s)$
the discriminant of the polynomial
![]() $ t \mapsto \widehat {T}_{s}(f)(t\mathbf {1}-\mathbf {y})$
. From (2.1) it follows that
$ t \mapsto \widehat {T}_{s}(f)(t\mathbf {1}-\mathbf {y})$
. From (2.1) it follows that
![]() $\Delta _{f}\!(\mathbf {y};s)$
defines an entire function in the (complex) variable s. Hence, either there is a positive number
$\Delta _{f}\!(\mathbf {y};s)$
defines an entire function in the (complex) variable s. Hence, either there is a positive number
![]() $\delta (\mathbf {y})$
for which
$\delta (\mathbf {y})$
for which
![]() $\Delta _{f}\!(\mathbf {y};s) \neq 0$
whenever
$\Delta _{f}\!(\mathbf {y};s) \neq 0$
whenever
![]() $0<|s|<\delta (\mathbf {y})$
or
$0<|s|<\delta (\mathbf {y})$
or
![]() $\Delta _{f}\!(\mathbf {y};s)$
is identically zero. The latter cannot happen since then, by letting
$\Delta _{f}\!(\mathbf {y};s)$
is identically zero. The latter cannot happen since then, by letting
![]() $s \to \infty $
, it follows that the discriminant of the polynomial
$s \to \infty $
, it follows that the discriminant of the polynomial
![]() $t \mapsto f_{n}^{d}(t\mathbf {1} -\mathbf {y})$
is equal to zero, which contradicts the fact that
$t \mapsto f_{n}^{d}(t\mathbf {1} -\mathbf {y})$
is equal to zero, which contradicts the fact that
![]() $f_{n}^{d}(\mathbf {w})$
is in the interior of
$f_{n}^{d}(\mathbf {w})$
is in the interior of
![]() $\mathbb {P}\mathrm {S}^{d}_{n}$
. By compactness (of
$\mathbb {P}\mathrm {S}^{d}_{n}$
. By compactness (of
 $\mathbb {S}^{n-2}_{\mathbf {1}}$
) and Hurwitz’s theorem on the continuity of zeros, it follows that there is a uniform
$\mathbb {S}^{n-2}_{\mathbf {1}}$
) and Hurwitz’s theorem on the continuity of zeros, it follows that there is a uniform
![]() $\delta>0$
such that
$\delta>0$
such that
![]() $\Delta _{f}\!(\mathbf {y};s) \neq 0$
whenever
$\Delta _{f}\!(\mathbf {y};s) \neq 0$
whenever
![]() $0<|s|<\delta $
and
$0<|s|<\delta $
and
 $\mathbf {y} \in \mathbb {S}^{n-2}_{\mathbf {1}}$
. Hence,
$\mathbf {y} \in \mathbb {S}^{n-2}_{\mathbf {1}}$
. Hence,
![]() $\widehat {T}_{s}(f)$
is in the interior of
$\widehat {T}_{s}(f)$
is in the interior of
![]() $\mathbb {P}\mathrm {S}^{d}_{n}$
for all
$\mathbb {P}\mathrm {S}^{d}_{n}$
for all
![]() $0<s<\delta $
.
$0<s<\delta $
.
5. Discussion
The support of a polynomial
![]() $\sum _{\alpha \in \mathbb {N}^{n}} a_{\alpha } w_{1}^{\alpha _{1}} \cdots w_{n}^{\alpha _{n}}$
is
$\sum _{\alpha \in \mathbb {N}^{n}} a_{\alpha } w_{1}^{\alpha _{1}} \cdots w_{n}^{\alpha _{n}}$
is
![]() $\mathrm {J}= \{ \alpha \mid a_{\alpha } \neq 0\}$
. There is a one-to-one correspondence between the supports of polynomials in
$\mathrm {J}= \{ \alpha \mid a_{\alpha } \neq 0\}$
. There is a one-to-one correspondence between the supports of polynomials in
![]() $\mathbb {P}\mathrm {L}^{d}_{n}$
and
$\mathbb {P}\mathrm {L}^{d}_{n}$
and
![]() $\mathrm {M}$
-convex sets in
$\mathrm {M}$
-convex sets in
![]() $\Delta _{n}^{d}=\{\alpha \in \mathbb {N}^{n} \mid \alpha _{1}+\cdots +\alpha _{n}=d\}$
; see [Reference Brändén and Huh7, Theorem 3.10]. Let
$\Delta _{n}^{d}=\{\alpha \in \mathbb {N}^{n} \mid \alpha _{1}+\cdots +\alpha _{n}=d\}$
; see [Reference Brändén and Huh7, Theorem 3.10]. Let
![]() $\mathbb {P}\mathrm {L}_{\mathrm {J}}$
be the space of polynomials in
$\mathbb {P}\mathrm {L}_{\mathrm {J}}$
be the space of polynomials in
![]() $\mathbb {P}\mathrm {L}^{d}_{n}$
with support
$\mathbb {P}\mathrm {L}^{d}_{n}$
with support
![]() $\mathrm {J}$
. Hence,
$\mathrm {J}$
. Hence,
 $$ \begin{align*}\mathbb{P}\mathrm{L}^{d}_{n} = \bigsqcup_{\mathrm{J}}\mathbb{P}\mathrm{L}_{\mathrm{J}}, \end{align*} $$
$$ \begin{align*}\mathbb{P}\mathrm{L}^{d}_{n} = \bigsqcup_{\mathrm{J}}\mathbb{P}\mathrm{L}_{\mathrm{J}}, \end{align*} $$
where the disjoint union is over all
![]() $\mathrm {M}$
-convex sets in
$\mathrm {M}$
-convex sets in
![]() $\Delta _{n}^{d}$
. The space
$\Delta _{n}^{d}$
. The space
![]() $\mathbb {P}\mathrm {L}_{\mathrm {J}}$
is nonempty and contractible for each
$\mathbb {P}\mathrm {L}_{\mathrm {J}}$
is nonempty and contractible for each
![]() $\mathrm {J}$
[Reference Brändén and Huh7, Theorem 3.10 and Proposition 3.25].
$\mathrm {J}$
[Reference Brändén and Huh7, Theorem 3.10 and Proposition 3.25].
Similarly, there is a one-to-one correspondence between the supports of polynomials in
 $\mathbb {P}\underline {\mathrm {L}}^{d}_{n}$
and rank d matroids on
$\mathbb {P}\underline {\mathrm {L}}^{d}_{n}$
and rank d matroids on
![]() $[n]$
. Let
$[n]$
. Let
![]() $\mathbb {P}\underline {\mathrm {L}}_{\mathrm {M}}$
be the space of polynomials in
$\mathbb {P}\underline {\mathrm {L}}_{\mathrm {M}}$
be the space of polynomials in
 $\mathbb {P}\underline {\mathrm {L}}^{d}_{n}$
whose support is the set of bases of
$\mathbb {P}\underline {\mathrm {L}}^{d}_{n}$
whose support is the set of bases of
![]() $\mathrm {M}$
. Then
$\mathrm {M}$
. Then
 $$ \begin{align*}\mathbb{P}\underline{\mathrm{L}}^{d}_{n} = \bigsqcup_{\mathrm{M}}\mathbb{P}\underline{\mathrm{L}}_{\mathrm{M}}, \end{align*} $$
$$ \begin{align*}\mathbb{P}\underline{\mathrm{L}}^{d}_{n} = \bigsqcup_{\mathrm{M}}\mathbb{P}\underline{\mathrm{L}}_{\mathrm{M}}, \end{align*} $$
where the union is over all matroids of rank d on
![]() $[n]$
. The space
$[n]$
. The space
![]() $\mathbb {P}\underline {\mathrm {L}}_{\mathrm {M}}$
is nonempty and contractible for each
$\mathbb {P}\underline {\mathrm {L}}_{\mathrm {M}}$
is nonempty and contractible for each
![]() $\mathrm {M}$
[Reference Brändén and Huh7, Theorem 3.10 and Proposition 3.25].
$\mathrm {M}$
[Reference Brändén and Huh7, Theorem 3.10 and Proposition 3.25].
Postnikov [Reference Postnikov17] proved that there is a similar stratification of the totally nonnegative Grassmannian into closed cells corresponding to matroids that are realisable by real matrices whose maximal minors are all nonnegative. He conjectured that these cells are homeomorphic to closed Euclidean balls. The conjecture was recently proved by Galashin, Karp and Lam [Reference Galashin, Karp and Lam11] in a more general setting. The next questions are Lorentzian analogs of Postnikov’s conjecture.
Question 5.1. Let
![]() $\mathrm {J}$
in
$\mathrm {J}$
in
![]() $\Delta _{n}^{d}$
be an
$\Delta _{n}^{d}$
be an
![]() $\mathrm {M}$
-convex set. Is the closure of
$\mathrm {M}$
-convex set. Is the closure of
![]() $\mathbb {P}\mathrm {L}_{\mathrm {J}}$
homeomorphic to a closed Euclidean ball?
$\mathbb {P}\mathrm {L}_{\mathrm {J}}$
homeomorphic to a closed Euclidean ball?
In this article we settled the case of Question 5.1 when
![]() $\mathrm {J}=\Delta _{n}^{d}$
. Since the polynomial
$\mathrm {J}=\Delta _{n}^{d}$
. Since the polynomial
![]() ${n^{-d}(w_{1}+\cdots +w_{n})^{d}}$
has full support and lies on the boundary of
${n^{-d}(w_{1}+\cdots +w_{n})^{d}}$
has full support and lies on the boundary of
![]() $\mathbb {P}\mathrm {L}^{d}_{n}$
, it follows that the interiors of
$\mathbb {P}\mathrm {L}^{d}_{n}$
, it follows that the interiors of
![]() $\mathbb {P}\mathrm {L}_{\mathrm {J}}$
do not form a cell decomposition of
$\mathbb {P}\mathrm {L}_{\mathrm {J}}$
do not form a cell decomposition of
![]() $\mathbb {P}\mathrm {L}_{\mathrm {J}}$
. This suggests the following question.
$\mathbb {P}\mathrm {L}_{\mathrm {J}}$
. This suggests the following question.
Question 5.2. Is there a refinement of the decomposition given by the interiors of
![]() $\mathbb {P}\mathrm {L}_{\mathrm {J}}$
, that to form a cell decomposition, and ideally a regular CW complex?
$\mathbb {P}\mathrm {L}_{\mathrm {J}}$
, that to form a cell decomposition, and ideally a regular CW complex?
These questions have multiaffine analogs.
Question 5.3. Let
![]() $\mathrm {M}$
be a matroid on
$\mathrm {M}$
be a matroid on
![]() $[n]$
. Is the closure of
$[n]$
. Is the closure of
![]() $\mathbb {P}\underline {\mathrm {L}}_{\mathrm {M}}$
homeomorphic to a closed Euclidean ball?
$\mathbb {P}\underline {\mathrm {L}}_{\mathrm {M}}$
homeomorphic to a closed Euclidean ball?
In this article we settled the case of Question 5.3 when
![]() $\mathrm {M}$
is uniform.
$\mathrm {M}$
is uniform.
Question 5.4. Is there a refinement of the decomposition given by the interiors of
![]() $\mathbb {P}\underline {\mathrm {L}}_{\mathrm {M}}$
, that to form a cell decomposition, and ideally a regular CW complex?
$\mathbb {P}\underline {\mathrm {L}}_{\mathrm {M}}$
, that to form a cell decomposition, and ideally a regular CW complex?
We also have a stratification
 $$ \begin{align*} \mathbb{P}\mathrm{S}^{d}_{n} = \bigsqcup_{\mathrm{J}}\mathbb{P}\mathrm{S}_{\mathrm{J}}, \end{align*} $$
$$ \begin{align*} \mathbb{P}\mathrm{S}^{d}_{n} = \bigsqcup_{\mathrm{J}}\mathbb{P}\mathrm{S}_{\mathrm{J}}, \end{align*} $$
where the union is over all
![]() $\mathrm {M}$
-convex sets in
$\mathrm {M}$
-convex sets in
![]() $\Delta _{n}^{d}$
that occur as supports of polynomials in
$\Delta _{n}^{d}$
that occur as supports of polynomials in
![]() $\mathbb {P}\mathrm {S}^{d}_{n}$
. Is the space
$\mathbb {P}\mathrm {S}^{d}_{n}$
. Is the space
![]() $\overline {\mathbb {P}\mathrm {S}_{\mathrm {J}}}$
homeomorphic to a closed Euclidean ball? Is it contractible? Similar questions could be asked for the analogous spaces of multiaffine homogeneous and real stable polynomials. Let
$\overline {\mathbb {P}\mathrm {S}_{\mathrm {J}}}$
homeomorphic to a closed Euclidean ball? Is it contractible? Similar questions could be asked for the analogous spaces of multiaffine homogeneous and real stable polynomials. Let
 $\mathbb {P}\underline {\mathrm {S}}^{d}_{n}$
be the space of all multiaffine polynomials in
$\mathbb {P}\underline {\mathrm {S}}^{d}_{n}$
be the space of all multiaffine polynomials in
![]() $\mathbb {P}\mathrm {S}^{d}_{n}$
. In particular, we have the following.
$\mathbb {P}\mathrm {S}^{d}_{n}$
. In particular, we have the following.
Conjecture 5.5. The space
 $\mathbb {P}\underline {\mathrm {S}}^{d}_{n}$
is homeomorphic to a closed Euclidean ball.
$\mathbb {P}\underline {\mathrm {S}}^{d}_{n}$
is homeomorphic to a closed Euclidean ball.
Equivalently, in the terminology of [Reference Borcea, Brändén and Liggett6], Conjecture 5.5 says that the space of strongly Rayleigh measures on
![]() $\{1,\ldots , n\}$
, with constant sum d, is homeomorphic to a closed Euclidean ball.
$\{1,\ldots , n\}$
, with constant sum d, is homeomorphic to a closed Euclidean ball.
Acknowledgements
Thanks to two anonymous referees who spotted some mistakes in an earlier version of this article and whose suggestions significantly improved the quality of the article. The author is a Wallenberg Academy Fellow supported by the Knut and Alice Wallenberg Foundation and the Göran Gustafsson Foundation.
Conflict of Interest
None.




