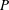Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-22T10:28:44.776Z Has data issue: false hasContentIssue false
  • English
  • Français

SUR LES COMPOSANTES CONNEXES D’UNE FAMILLE D’ESPACES ANALYTIQUES ${P}$-ADIQUES

Part of: Arithmetic problems. Diophantine geometry

Published online by Cambridge University Press:  29 May 2014

JÉRÔME POINEAU
JÉRÔME POINEAU*
Affiliation:
Institut de recherche mathématique avancée, 7, rue René Descartes, 67084 Strasbourg, France; jerome.poineau@math.unistra.fr

Résumé

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Soit 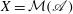$X=\mathcal{M}(\mathscr{A})$ un espace affinoïde et soient 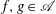$f,g\in \mathscr{A}$. Nous étudions les ensembles de composantes connexes des espaces définis par une inégalité de la forme 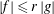$|f|\le r\, |g|$, avec 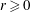$r\ge 0$. Nous montrons qu’il existe une partition finie de 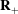$\mathbf{R}_{+}$ en intervalles sur lesquels ces ensembles sont canoniquement en bijection et que les bornes de ces intervalles appartiennent à 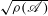$\sqrt{\rho (\mathscr{A})}$.

Abstract

On the connected components of a family of$\boldsymbol {p}$-adic analytic spaces. Let 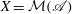$X=\mathcal{M}(\mathscr{A})$ be an affinoid space and let $f,g\in \mathscr{A}$. We study the sets of connected components of the spaces defined by an inequality of the form $|f|\le r\, |g|$, with $r\ge 0$. We prove that there exists a finite partition of $\mathbf{R}_{+}$ into intervals where those sets are canonically in bijection and that the bounds of those intervals belong to $\sqrt{\rho (\mathscr{A})}$.

MSC classification

Secondary: 14G22: Rigid analytic geometry
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 2 , 01 July 2014 , e14
Creative Commons
Creative Common License - CCCreative Common License - BY
The online version of this article is published within an Open Access environment subject to the conditions of the Creative Commons Attribution licence .
Copyright
© The Author 2014

References

Références

Abbes, A. and Saito, T., ‘Ramification of local fields with imperfect residue fields’, Amer. J. Math. 124 (2002), 879–920.CrossRefGoogle Scholar
Bartenwerfer, W., ‘Einige Fortsetzungssätze in der $p$ -adischen analysis’, Math. Ann. 185 (1970), 191–210.CrossRefGoogle Scholar
Berkovich, V. G., ‘Spectral theory and analytic geometry over non-Archimedean fields’, in:Mathematical Surveys and Monographs, Vol. 33 (American Mathematical Society, Providence, RI, 1990).Google Scholar
Berkovich, V. G., ‘Étale cohomology for non-Archimedean analytic spaces’, Inst. Hautes Études Sci. Publ. Math. 78 (1993), 5–161.Google Scholar
Berkovich, V. G., ‘Smooth $p$ -adic analytic spaces are locally contractible’, Invent. Math. 137 (1999), 1–84.Google Scholar
Bosch, S., ‘Eine bemerkenswerte Eigenschaft der formellen Fasern affinoider Räume’, Math. Ann. 229 (1977), 25–45.Google Scholar
Bosch, S., Güntzer, U. and Remmert, R., ‘Non-Archimedean analysis’, in:Grundlehren der Mathematischen Wissenschaften, A systematic approach to rigid analytic geometry 261 (Springer-Verlag, Berlin, 1984).Google Scholar
Bosch, S., Lütkebohmert, W. and Raynaud, M., ‘Formal and rigid geometry. IV. The reduced fibre theorem’, Invent. Math. 119 (1995), 361–398.Google Scholar
Conrad, B. and Temkin, M., 2010. Descent for non-Archimedean analytic spaces. http://math.stanford.edu/∼conrad/papers/descentnew.pdf, http://www.math.huji.ac.il/∼temkin/papers/Descent.pdf.Google Scholar
Ducros, A., ‘Parties semi-algébriques d’une variété algébrique $p$ -adique’, Manuscripta Math. 111 (2003), 513–528.Google Scholar
Ducros, A., ‘Variation de la dimension relative en géométrie analytique $p$ -adique’, Compos. Math. 143 (2007), 1511–1532.Google Scholar
Ducros, A., ‘Les espaces de Berkovich sont modérés, d’après E. Hrushovksi et F. Loeser’, Sém. Bourbaki (2012), Exp. 1056.Google Scholar
Epp, H. P., ‘Eliminating wild ramification’, Invent. Math. 19 (1973), 235–249.CrossRefGoogle Scholar
Hrushovski, E. and Loeser, F., 2010. Non-Archimedean tame topology and stably dominated types. arxiv:http://arxiv.org/abs/1009.0252.Google Scholar
Lütkebohmert, W., ‘Der Satz von Remmert-Stein in der nichtarchimedischen Funktionentheorie’, Math. Z. 139 (1974), 69–84.Google Scholar
Poineau, J., ‘Un résultat de connexité pour les variétés analytiques $p$ -adiques: privilège et noethérianité’, Compos. Math. 144 (2008), 107–133.Google Scholar
Temkin, M., ‘On local properties of non-Archimedean analytic spaces. II’, Israel J. Math. 140 (2004), 1–27.Google Scholar