1. Introduction
As identification of quantitative trait loci (QTL) becomes routine, genotype-assisted selection (GAS) has become possible and even desirable for populations with managed breeding. GAS is where the frequency of a known allele, which affects the trait of selection, is managed generation by generation within the population, often to fixation. One of the known hurdles of the application of GAS is the Gibson effect, a phenomenon whereby GAS results in higher short-term genetic gain but lower long-term genetic gain than conventional selection methods that ignore the information on QTL (Gibson, Reference Gibson1994). The explanation is, although GAS can fix the QTL in shorter time, the loss of variation on polygenes associated with the strong positive selection of QTL will lead to reduced selection response on polygenes, which cannot be fully recovered. Various authors have shown that this effect can be ameliorated by optimizing the selection procedures for the QTL over multiple generations, i.e. the optimization of allele trajectory (Dekkers & van Arendonk, Reference Dekkers and van Arendonk1998; Dekkers & Chakraborty, Reference Dekkers and Chakraborty2001; Villanueva et al., Reference Villanueva, Dekkers, Woolliams and Settar2002, Reference Villanueva, Dekkers, Woolliams and Settar2004; Meuwissen & Sonesson, Reference Meuwissen and Sonesson2004; Sanchez et al., Reference Sanchez, Caballero and Santiago2006).
This optimization process has led to a variety of approaches to manage the trajectory: maximizing progress over the long term (Pong-Wong & Woolliams, Reference Pong-Wong and Woolliams1998; Villanueva et al., Reference Villanueva, Dekkers, Woolliams and Settar2004), with predefined time horizons (Dekkers & van Arendonk, Reference Dekkers and van Arendonk1998); or constrained to a constant rate of inbreeding (Villanueva et al., Reference Villanueva, Dekkers, Woolliams and Settar2002). These studies make selection decisions based on estimated breeding values in one form or another, so optimum allele trajectory is therefore defined only implicitly. However, the method of Dekkers & van Arendonk (Reference Dekkers and van Arendonk1998) allows the optimized trajectory to be defined explicitly as a set of time points for the allele frequency, so defining the selection pressure that is directly applied to the allele to be analysed. Based on an observation of Dekkers & van Arendonk (Reference Dekkers and van Arendonk1998), Meuwiseen & Sonesson (Reference Meuwissen and Sonesson2004) directly defined the allele trajectory by making selection intensity on the allele constant over the period of selection. More recently, Sanchez et al. (Reference Sanchez, Caballero and Santiago2006) pointed out that the effective population size was inversely proportional to the square of selection intensity, so that the optimum trajectory to minimize the accumulated inbreeding due to fixation should minimize the average squared selection intensity on the major gene over generations up to the given fixation time; in other words, it should minimize the sum of squared selection intensities (simplified as the sum of squared intensities hereafter) applied to the allele over generations.
A common theme to these studies of allele trajectories is that they use discrete generation models. This discrete time model imposes limitations on obtaining analytical solutions for the problem of approximating the optimal pathway, and the lack of analytical solution leaves unresolved the degree to which these approaches are distinct. Furthermore, the iterative solutions from the equalizing selection intensities method leave open questions such as what is the total selection intensity (simplified as total intensity thereafter) required to fix the QTL given the circumstances. Therefore, this study establishes a continuous time model of the process of fixing an allele, and explicitly optimizes the trajectory with respect to various objective functions of the selection intensity applied to the gene using the calculus of variations. This continuous model serves as a common platform allowing further investigation and comparison between different optimizing objectives. The predictions from the continuous time model are compared to optimizations using discrete generations to quantify the precision of the continuous time model.
2. Method
(i) Theory
(a) Continuous approximations
Consider the process of moving a desired allele Q from frequency p 0 at time 0 to p T at time T in discrete generations and assume, for simplicity of notation, that there is only one other allele, q, at that locus. The trajectory consists of the set of frequency points {p t, t=0,…,T} and optimization of the trajectory is the set of p t that maximize a certain objective function. Commonly, when considering fixation of alleles in GAS, p 0=(2N)−1 and p T=1, as it models the fixing of a new mutation occurring in a diploid population of size N. This scenario is equivalent to the situation of eliminating a known allele from a population (0<p 0<1 and p T=0), as removing one allele forces the frequency of all alternative alleles to 1. However, the theory developed here will not be specific to these starting and finishing frequencies.
In this paper, following Meuwissen & Sonesson (Reference Meuwissen and Sonesson2004) and Sanchez et al. (Reference Sanchez, Caballero and Santiago2006), the objective functions considered are functions of the selection intensity applied directly to the allele. Let p t,k be the frequency of the Q allele of individual k born at time t, so p t,k will take values 0, 1/2 or 1 depending on whether k has genotype qq, qQ or QQ. Using p t,k as the definition of an additive trait of selection, the population mean is p t, the variance is ![]() , the selection intensity i t can be defined as
, the selection intensity i t can be defined as
for t=0,…,T−1, and the trajectory is a sequence of points {p t, t=0,…,T}.
The trajectory can be considered in continuous time rather than as a set of discrete generations. It is an assumption, to be tested later, that the use of continuous time will approximate the original problem better as the selection opportunities for changing allele frequency become greater, i.e. when T is large. Let the trajectory over time be given by p(t), which is assumed to be a differentiable function of time t; then δp=p t+δt−p t≈p′(t) δt, where p′(t)=dp/dt and ![]() . Therefore provided the trajectory p(t) is differentiable so that its derivative, p′(t), exists, the sums over the trajectory may be approximated by integrals.
. Therefore provided the trajectory p(t) is differentiable so that its derivative, p′(t), exists, the sums over the trajectory may be approximated by integrals.
Different objective functions that optimize the trajectory are considered and analysed using the continuous approximation, including (1) the trajectory that minimizes the total intensity, (2) the trajectory that minimizes the sum of squared intensities and (3) the trajectory that equalizes selection intensity. Due to the amount of mathematical details involved, only the essential information and core equations are shown in this section; however, more details can be found in Appendix A.
(b) Minimizing the total intensity
The total intensity for fixing an allele with a trajectory p(t) as T becomes large can be given by
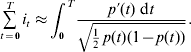
Transformation and integration of the above equation give the following:
Note that this solution only depends on the starting point p 0 and the ending point p T, suggesting that there is no such thing as minimizing the total intensity if the approximation is valid – the total intensity is fixed between a pair of frequency points regardless of its trajectory or the value of T. For a new mutation moving to fixation, p 0=(2N)−1 and p T=1, the total intensity applied to the allele during fixation is ![]() , which tends to
, which tends to ![]() as N becomes large, i.e. when the starting frequency approaches zero.
as N becomes large, i.e. when the starting frequency approaches zero.
(c) Minimizing the sum of squared intensities
The specific optimization considered by Sanchez et al. (Reference Sanchez, Caballero and Santiago2006) was the trajectory of the allele frequencies required to minimize the impact of the process on accumulated inbreeding during the fixation. It is assumed here that accumulated inbreeding can be well approximated from the summed rates of inbreeding (ΔF) achieved in each generation, and that the allele can be fully identified throughout the process so that its frequency can be explicitly managed over time. The value of ΔF will vary according to the impacts of all the different selection advantages inherent in a selection scheme, not only the carrier status of individuals for the allele of interest (Woolliams & Bijma, Reference Woolliams and Bijma2000), and will depend on the square of the selection intensities applied (Woolliams et al., Reference Woolliams, Wray and Thompson1993). Therefore, the objective of minimizing the impact of the fixation is to minimize ![]() , which can be shown as follows:
, which can be shown as follows:
Solving the above equation gives sin−1(1−2p)=At+B or, equivalently,
where A and B are constants of integration and vary depending on p 0, p T and T. Values of A and B can be obtained by substituting these parameters into eqn (5). For example, assume that fixation is desired from a new mutation, i.e. p 0=(2N)−1≈0 for large N, and p T=1. With these conditions B=π/2 and A=−π/T give ![]() . The optimal trajectory for minimizing the sum of squared intensities applied to the allele is therefore a segment of a sine wave.
. The optimal trajectory for minimizing the sum of squared intensities applied to the allele is therefore a segment of a sine wave.
(d) Equalizing selection intensities
Based on the observation from Dekkers & van Arendonk (Reference Dekkers and van Arendonk1998) that the selection intensities achieved in each generation are roughly constant in their simulated result with best long-term gain, Meuwissen & Sonesson (Reference Meuwissen and Sonesson2004) suggest optimizing the trajectory to maximize the cumulative selection response by making the selection intensities constant over time. Applying this objective in the continuous approximation gives a differential equation that is identical to that obtained above for the objective of minimizing the sum of squared intensities. This indicates that the objective from Meuwissen & Sonesson gives an optimum trajectory identical to that from minimizing the sum of squared intensities. This conclusion is analogous to the minimization of the sum of squares for n numbers whose sum is fixed to some value c – the solution has all numbers equal to c/n. Therefore, the theory suggests that as the continuous approximation becomes more apt, the distinction between the objectives of Sanchez et al. (Reference Sanchez, Caballero and Santiago2006) and Meuwissen & Sonesson (Reference Meuwissen and Sonesson2004) disappears. The question remains over how close an approximation.
(ii) Simulation methods
Two types of simulation methods are included in this section: (i) a genetic algorithm with small population size (N=10) and (ii) a simulation of breeding populations with large population size (N=500). Together they test the validity and robustness of the continuous approximation under various scenarios.
(a) Genetic algorithm
The genetic algorithm used differential evolution (Shepherd & Kinghorn, Reference Shepherd and Kinghorn1992) to optimize the allele frequency in order to find optimal trajectories with N=10, for the three objectives considered above: (i) equalizing selection intensities; (ii) minimizing the sum of squared intensities and (iii) minimizing total intensity. Equalizing the selection intensities was achieved by minimizing the sum of all squared differences among the selection intensities.
(b) Simulations of breeding schemes
Computer simulations of the breeding schemes start with a base population (t=0) of 500 diploid individuals, and this population size was maintained throughout the simulation. One individual from the base population was randomly chosen to carry a single copy of positive allele (initial frequency p 0=(2N)−1) with allelic effect a, which equals 0·5 as the addition or removal of one positive allele results in a change of 0·5 in terms of frequency. Random mating with possible selfing was assumed for simplicity, i.e. the genetic make-up of the offspring was randomly assigned from selected parents with replacement. As the theory shows that the objective of minimizing the sum of squared intensities resembles the objective of equalizing selection intensities when T is large, only the objective of equalizing selection intensities is used for its ease of execution. Other selection strategies with oscillating intensities in a sawtooth pattern, i.e. intensity profiles of the form {0·3, 0·1, 0·3, 0·1…}, were also employed to test whether the continuous approximation still holds under more extreme conditions.
One should note that the time unit applied in this study was the opportunities for selection and mating. Hence, the word cohort will be used hereafter to represent a group of animals that are the direct result of last selection and mating. The frequency of the positive allele was then calculated and recorded for each cohort, and simulation ended when the positive allele was either fixed (p t⩾(2N−1)/2N) or lost (p t⩽(2N)−1). In the case of the allele being lost, the data were excluded from the final dataset as we considered the pathway of allele fixation only. One thousand simulations were run for each set of parameters and the average number of cohorts required to fix the selected allele was obtained to be compared to the expected number of cohorts required from the approximation.
Discrete generation: A predefined constant selection intensity (i) was applied over every cohort by restricting the average frequency of the selected individuals. Calculation was then performed for each cohort to obtain the target p t+1 from the p t:
Selection candidates were composed of all individuals from the current cohort and were ranked according to their allelic value. Selection candidates were then removed sequentially from lower rank until the target p t+1 was achieved. However, as matings between selected parents are random, the average allele frequency in the resultant population could not be guaranteed and may deviate from the target p t+1. For oscillating intensities, a similar procedure as described above was used, except that the intensity is not constant over every cohort.
Overlapping generation: The overlapping generation model was largely identical to the discrete generation model except that the candidates available for selection were not only restricted to the current cohort but also extended to include two previous cohorts. For selection candidates with the same allelic value, a randomization process was used to determine which candidate would become a parent. Generation interval (L) was calculated as the age of parents (in units of cohorts) when the offspring was born.
When several cohorts contribute to the selection, the genetic variance is higher than shown in eqn (6), i.e. ![]() . Apart from the variance within all selected cohorts, the true genetic variance also contains an additional term for the variance between different cohorts:
. Apart from the variance within all selected cohorts, the true genetic variance also contains an additional term for the variance between different cohorts:
where E[p] denotes expectations over the selected cohorts. Simulations were carried out using eqn (6) with V total replacing ![]() . This was compared to using eqn (6) without modification.
. This was compared to using eqn (6) without modification.
3. Results
As shown in the theory, the continuous approximation provides a prediction for the total intensity required to move a target allele from a specific frequency to another. The prediction is only affected by the starting and ending frequencies, and is independent of T or N, although in the case of new mutation, the starting frequency is inversely related to the population size. Assuming fixation is the goal (i.e. the ending frequency is 1), the predicted total intensity is ![]() (≈4·44) for fixing a mutation in a large population and 3·80 for a starting frequency of 0·05.
(≈4·44) for fixing a mutation in a large population and 3·80 for a starting frequency of 0·05.
(i) Goodness of fit for small T, using the genetic algorithm
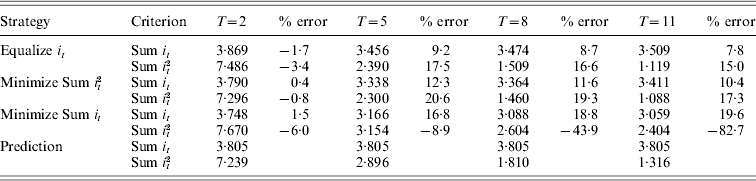
Table 1 summarizes and compares the results obtained from different GA evolutions and the continuous approximation for N=10, i.e. p 0=0·05, with small T values up to 11. For these parameters, the predicted total intensity from continuous approximation is 3·80 regardless of trajectory, in other words regardless of the objective functions of the GA evolution. When equalizing intensities across generations, the precision of predicting total intensity was very good initially with an error of 1·7% at T=2, deteriorating as T increases, and then improving again, with the greatest error of predicting the total intensity being 9·2% at T=5. The continuous approximation introduces marginally greater errors to the predicted total intensity when minimizing the sum of squared intensities, with errors peaking at 12·3% for T=5 and reducing to 10·4% for T=11. Note that the similar trend on the goodness of fit of the continuous approximation varies with T for both objectives. A very different trend was observed for the objective of minimizing total intensity, with total intensity continuing to reduce with T to 3·06 at T=11, which is very different from the prediction of 3·80. Reasons leading to this observation will be explained in the discussion section.
Table 1. The total intensity (Sum it) and the sum of squared intensities (Sum it2) required for N=10 and a range of T values, using three optimization strategies: (1) equalizing selection intensities across generations, (2) minimizing Sum it2, (3) minimizing Sum it and (4) calculated from the continuous approximation
Looking at the profile of these different GA evolutions reveals more details about them. The intensity profile of equalizing intensities is quite similar to minimizing the sum of squared intensities, with the intensity achieved each generation becoming more and more uniform over time (Fig. 1a and 1 b). This illustrates the derivation showing that the solutions for the two objectives converge, given the validity of the continuous approximation.
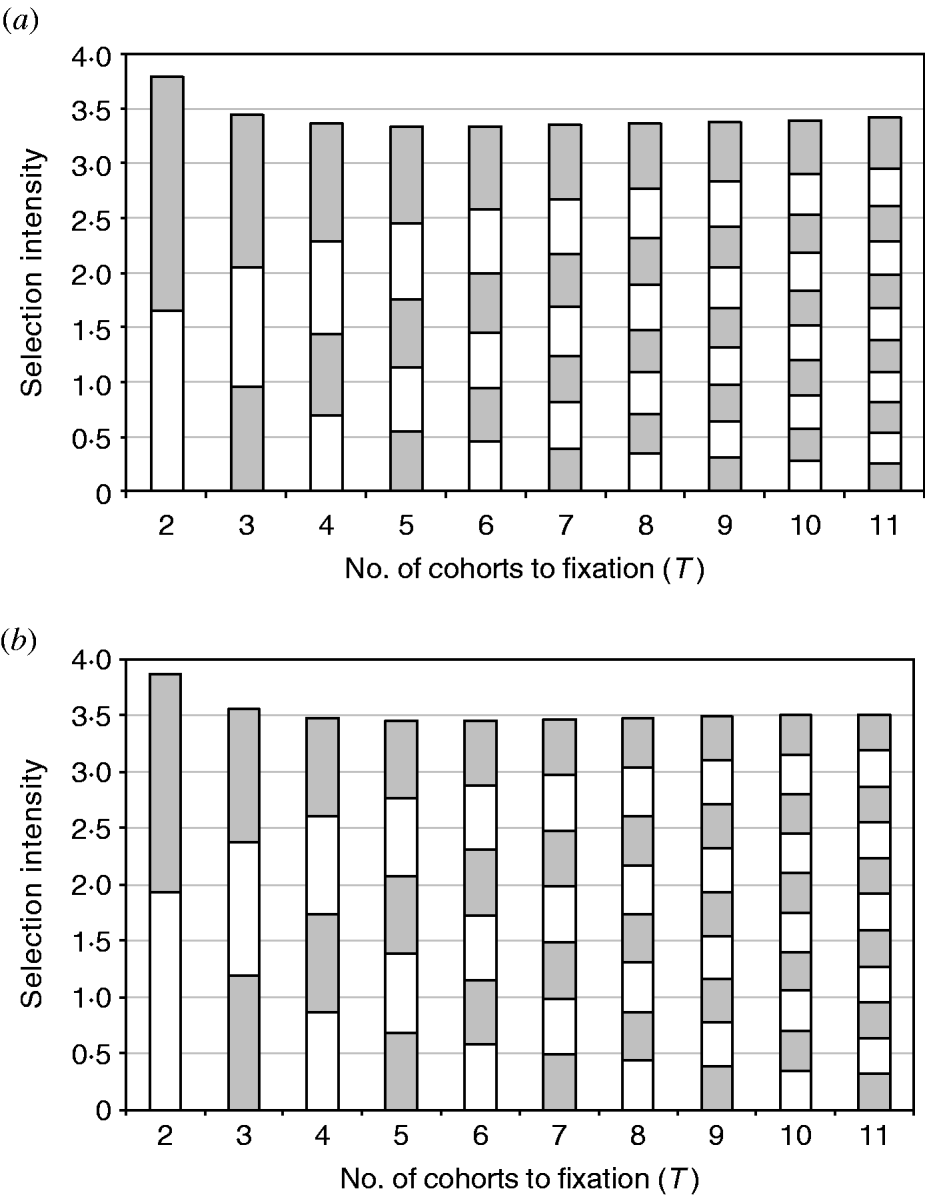
Figure 1. The composition of the total intensity obtained from GA with the objective of (a) minimizing the sum of squared intensities and (b) equalizing selection intensities. Each block represents the amount of selection intensity achieved in a single mating/frequency change. Shading is for the purpose of illustration only.
Assuming the convergence of objectives of equalizing intensities and minimizing the sum of squared intensities, the minimum sum of squared intensities predicted from the continuous approximation is equal to 3·802/T since (i/T)2T=i 2/T. Figure 1a shows that as T increases up to 11, the selection intensities become much more uniform, although Table 1 shows that the prediction of minimum sum of squared intensities still has significant error at T=11 despite the fact that the magnitude of the error is reducing. It might be expected that minimizing the sum of squared intensities will have approximately twice the error of minimizing the total intensity (see Appendix B).
(ii) Goodness of fit for large T, using simulations
The simulations allowed the goodness of fit to be tested for large T by varying the selection intensity applied. For the results presented in this section, p 0 is 0·001 (N=500), with the predicted total intensity being 4·35 from the continuous approximation.
(a) Discrete generation with constant selection intensity
The comparisons between the simulation of breeding with discrete generation and the continuous approximation for a range of different but constant selection intensities applied are shown in Figure 2. The results are presented as the mean number of cohorts required to fixation, with the expected number of cohorts being calculated by dividing the expected total intensity with the constant intensity applied during the simulation. Figure 2 shows that for constant intensities >0·5, where T<10, the scale of errors agrees with the result shown in Table 1. However, the simulations show that the approximation fits the results progressively more closely for all intensities <0·5. For all intensities <0·75, the differences between prediction and actual results are less than one cohort.
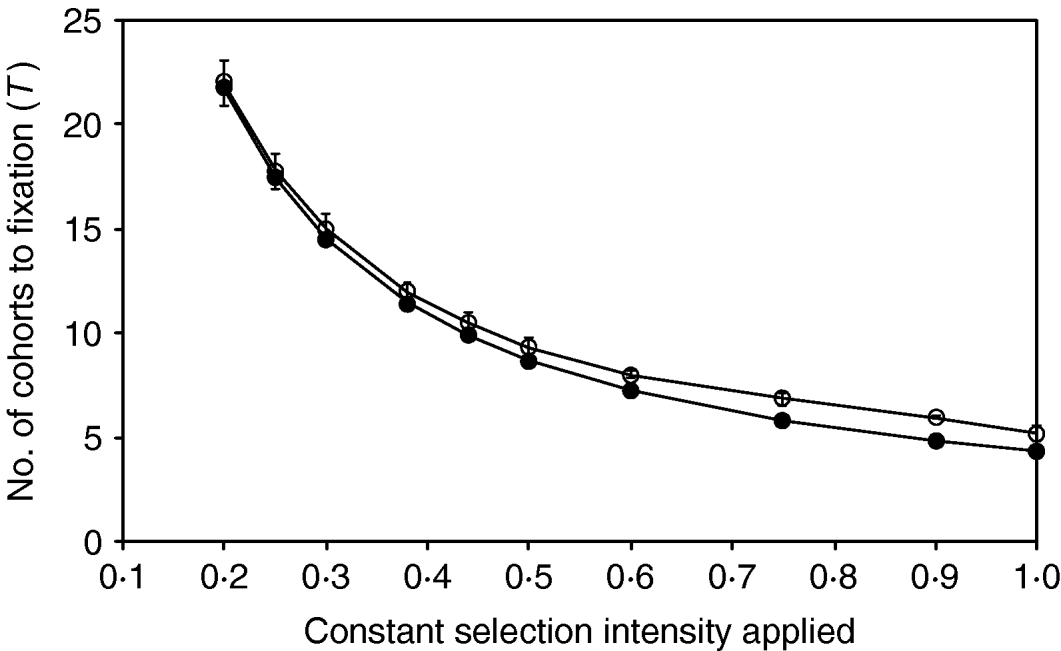
Figure 2. Comparison between the numbers of cohorts required to fix an allele for a range of different selection intensities, for (a) simulations with discrete generation (open circles) and (b) continuous approximation (filled circles). Population size (N) equals 500 in all cases. The standard deviations are shown as error bars and the standard errors are negligible.
(b) Discrete generation with oscillating selection intensity
The independence of the total intensity applied to a trajectory was further tested by oscillating selection intensities across cohorts as in a sawtooth pattern. Table 2 shows the comparison of total intensity applied for oscillating selection intensities patterns compared to constant selection intensity with the same pairwise average. Results show that the prediction errors are only slightly larger for oscillating selection intensities compared to constant selection intensities with comparable average selection intensity. The approximation still provides good prediction under such conditions, with errors around 2·3% for oscillating selection intensities {0·3, 0·1} that increased to 11·7% for selection intensities {0·6, 0·4}. The increase in error with higher selection intensities and lower fixation times would be expected from the result of constant selection intensities. There were only small differences between complementary patterns, i.e. {0·3, 0·1} compared to {0·1, 0·3} (results not shown).
Table 2. Comparison between the total intensity (Sum it) required to fix an allele under simulations with discrete generations and predicted from continuous approximation for a range of different selection intensities. The selection intensity can be either constant all through the simulation or oscillating between a pair of different values (shown as {a, b}). Population size (N) equals 500 in all cases

In all breeding simulations, the prediction often appears as an under-estimation of the simulated result, which is unsurprising because the selection intensity applied in the simulation could not always be achieved, i.e. in the last few cohorts the target p could exceed 1·0 in order to achieve the selection intensity applied – which is not possible. This is particularly important for large i selection, when only small selection intensity might have been required to move the frequency to 1.
(iii) Overlapping generation
Table 3 summarizes the results for simulations with overlapping generations. It shows that the total intensity required for fixation is predictable from the continuous approximation for low selection intensities, but the % errors increase as the selection intensity applied per cohort increases. When the unmodified eqn (6) was used, the result is almost identical to those shown in Figure 2. However the use of V total, which represents the full genetic variance, introduces an additional error. The 8·4% error for an intensity of 0·5 represents approximately 1 cohort difference between predicted and observed time to fixation. In this case, the mean actual number of cohorts was 9·4.
Table 3. A comparison between the total intensity (Sum it) required to fix an allele in simulations with overlapping generations for different constant selection intensities applied and for genetic variance calculated by different methods. In ‘Unmodified’ eqn (6) was used directly, but in ‘Modified’ the true genetic variance Vtotal replaced ![]() in eqn (6). In all cases population size (N) equals 500 and predicted Sum it=4·35. Standard errors, % error in prediction and generation interval (L) are also shown
in eqn (6). In all cases population size (N) equals 500 and predicted Sum it=4·35. Standard errors, % error in prediction and generation interval (L) are also shown

4. Discussion
The theory developed in this paper shows that provided the continuous approximation is valid, then the total intensity applied to move between two frequencies is directly proportional to the difference between the arcsines of (1−2p) for the end points p 0 and p T irrespective of trajectory – including standard logistic trajectories, dp/dt=sp(1−p). For fixation of a rare mutant, a frequent subject of interest, as p 0 tends to 0 and p T tends to 1, the total intensity tends to ![]() . Further the strategies of (i) equalizing selection intensities throughout the trajectory (Meuwissen & Sonesson, Reference Meuwissen and Sonesson2004) and (ii) minimizing the sum of squared intensities (Sanchez et al., Reference Sanchez, Caballero and Santiago2006) converge to the same optimal trajectory, which is a function of time described by a segment of a sine wave. The results showed that the goodness of fit of the continuous approximation became progressively better as T increased, with prediction errors for total intensity reducing and becoming reasonable as T~10, or average i~0·4 during the period. Further this result remained true for trajectories in which i was varied over time rather than constant, or where generations were overlapping rather than discrete.
. Further the strategies of (i) equalizing selection intensities throughout the trajectory (Meuwissen & Sonesson, Reference Meuwissen and Sonesson2004) and (ii) minimizing the sum of squared intensities (Sanchez et al., Reference Sanchez, Caballero and Santiago2006) converge to the same optimal trajectory, which is a function of time described by a segment of a sine wave. The results showed that the goodness of fit of the continuous approximation became progressively better as T increased, with prediction errors for total intensity reducing and becoming reasonable as T~10, or average i~0·4 during the period. Further this result remained true for trajectories in which i was varied over time rather than constant, or where generations were overlapping rather than discrete.
The continuous approximation will have a lack of fit for two reasons. First, a smooth curve is used to approximate a step function; second, the dominator for p t+1−p t in i t is related to p t(1−p t), not ![]() , which would be more natural for the use of the continuous approximation. This affects the goodness of fit under positive selection since i t is greater than expected from the approximation by
, which would be more natural for the use of the continuous approximation. This affects the goodness of fit under positive selection since i t is greater than expected from the approximation by ![]() , but less than the approximation when
, but less than the approximation when ![]() . The sizes of error are comparable for the pair of p(t) that are in equal deviation from 0·5. These trends are most extreme for p close to 0 or 1, or for small T when p(t) changes rapidly, and there are greater opportunities for cancelling when trajectories move from p<0·5 to p>0·5.
. The sizes of error are comparable for the pair of p(t) that are in equal deviation from 0·5. These trends are most extreme for p close to 0 or 1, or for small T when p(t) changes rapidly, and there are greater opportunities for cancelling when trajectories move from p<0·5 to p>0·5.
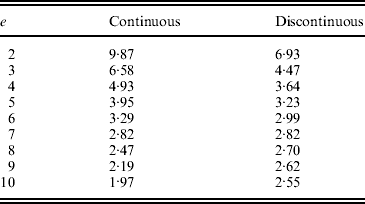
The difference in the sign of errors when p is greater than or less than 0·5 helps explain the results found for minimizing the total intensity, since for all T a trajectory with total intensity less than that predicted by the continuous approximation can be found (Table 1). Figure 3 shows the trajectories that minimize the total intensity shown in Table 1, and it is seen that the trajectory resembles a continuous curve for p<0·5 with a jump in the final generation from close to 0·5 directly to 1. As T increases, this represents a discontinuity in the trajectory, which can be seen as a combination of the continuous approximation from p 0 (assumed <0·5) to 0·5 and a direct jump from 0·5 to 1. For T=11 used in Table 1, the expected value from the discontinuous solution is 3·02 (cf. 3·06), affirming that the continuous approximation can fit well to intervals that do not span both sides of 0·5.
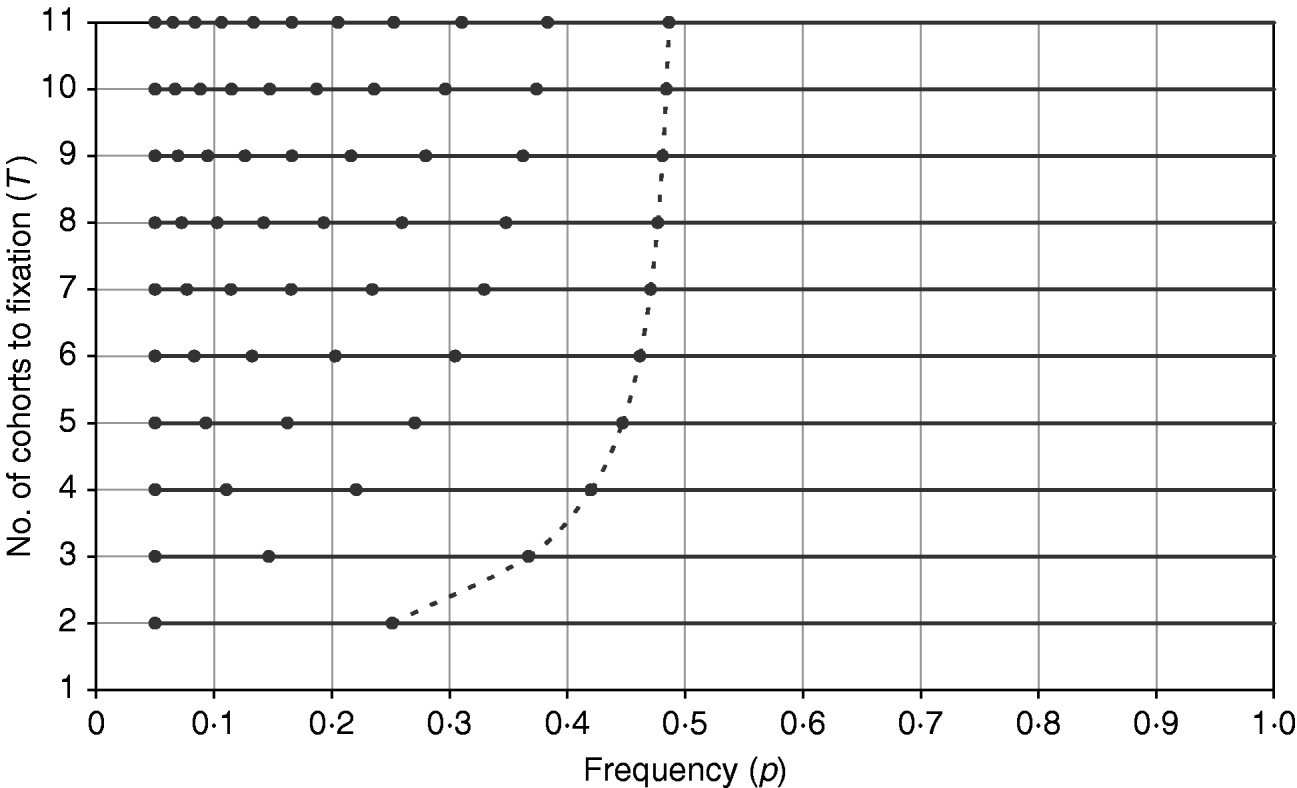
Figure 3. The frequency path (trajectory) obtained by GA with the objective of minimizing the total intensity for different T values. For each profile with different T, the frequency points are shown as solid circles along the horizontal line, with the first frequency point being at p=0·05. The last frequency points, p T−1, from all profiles are joined by a dashed line to illustrate how p T−1 approaches 0·5 as T increases.
The existence of the discontinuous solution for minimizing the total intensity creates a distinction between minimizing the sum of squared intensities and equalizing selection intensities. The sum of squared intensities can be broken down into two components: the sum of selection intensity and the variance of selection intensity:
The strategy of equalizing selection intensities promotes reduction in the sum of squared intensities by having no variance term, while the discontinuous solution is effective through reducing the total intensity. For small T, the trajectory minimizing the sum of squared intensities is temporarily effective in reducing the sum of squared intensities by reducing the total intensity acquired and therefore allowing some variance. However, as T increases, the benefits from reducing the total intensity become less than the penalty from the variance among the selection intensities, and the optimum trajectory moves towards the trajectory of equalizing intensities (see Appendix D).
Genomics is at the start of giving values to many small segments of chromosomes, sometimes with QTL identified and sometimes simply marked. Simultaneously, we are also at the threshold of being able to manage inbreeding at the level of the segment, i.e. requiring a slow change in diversity, or wishing to reduce the impact of negative LD on what segments can be fixed in the population. Therefore, we envisage the field of ‘designer genomes’, where the target trajectories of multiple loci are mapped out on a genome-wide scale. This is not a problem with only one locus. However, to achieve targets on frequency and inbreeding at multiple loci, we need to understand, in the long term, what is required to fix/eradicate an allele or to move from a frequency point to another, and hence consider how closely the designed genome can be achieved. It is precisely this approximation that allows such predictions over time to be made in a simple fashion albeit it is but one step towards achieving the wider goal.
One of the possible uses of this approximation is on the removal of the recessive mutant allele that causes foal immunodeficiency syndrome (FIS), more commonly known as the Fell pony syndrome. This fatal condition affects not only Fell ponies but also Dales ponies, and the causal mutant has recently been identified (June Swinburne, personal communication). Although the eradication of this mutant allele is highly desirable, two reasons make the execution difficult: first, the frequency of the carrier is high within the population (~0·4 in the Fell breed, June Swinburne, personal communication), and second, the Fell breed is a small breed. In other words, this allele is widespread in a small gene pool; hence options such as culling of all carriers are not sensible as they might lead to the loss of genetic diversity and the emergence of new recessives. Therefore, it is necessary to plan the removal of this mutant allele over a prior timescale to minimize the impact on diversity. Theoretically, the process of eradication should be carried out slowly and carefully in order to minimize the reduction on genetic diversity within the breeds. The approximation in this study can provide a simple means of obtaining a series of stage goals for moving the frequency to zero, i.e. target frequency points, to be achieved over the pre-determined horizon while minimizing the diversity loss. With the mutant allele frequency ~0·25, the total intensity required to remove the mutant allele is ~1·48, and the intensity in each generation is 1·48/T.
Aspects of the results may be generalized to more than one QTL, and there is a synergy with the results of Goddard (Reference Goddard2009), where trajectories for two QTLs are optimized with respect to a profit function. The study of Goddard recognizes that allele frequencies do not change linearly with the selection intensity applied, and uses a transformation to a scale (denoted z in the paper) upon which linearity holds – this requires the continuous approximation to hold since derivatives are required. Appendix C shows that the scale, z(p), can be interpreted as being directly proportional to accumulated selection intensity applied to the locus for moving from an infinitesimally small frequency to p. This study shows that to move m loci from p0 to pT while minimizing inbreeding at a neutral locus (and one that is affected by selection through the development of the pedigree only) constant selection intensity is required to be simultaneously applied at each locus – albeit with intensity differing among loci. This trajectory is represented by straight lines in an m-dimensional z-space with the relative strength of selection on each locus determining direction, and the line is traversed in T segments of equal length. However, the actual inbreeding accumulated will depend on T, the size of the population, and also upon the linkage disequilibrium among the loci being selected.
In conclusion, the continuous approximation shows that (i) the optimizing approaches of equalizing intensities (Meuwissen & Sonesson, Reference Meuwissen and Sonesson2004) and minimizing the sum of squared intensities (Sanchez et al., Reference Sanchez, Caballero and Santiago2006) have the same limiting form and converge over time to a sine wave and (ii) the total intensity required to move an allele from a given frequency point to another can be very closely approximated and only depends on the starting and end frequency.
The BBSRC are gratefully acknowledged for funding.
Appendix A
(i) Minimizing the total intensity
By noting that p′(t) dt can be replaced by dp, and then substituting p for p(t), eqn (2) can be transformed to the following equation, where its direct integration leads to eqn (3):
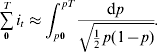
(ii) Minimizing properties of allele trajectories
An important methodology for optimizing trajectories is the calculus of variations (Weisstein, Reference Weisstein2005). When the function to be optimized is of the form
the solution can be obtained from the Euler–Lagrange equations provided trajectories p(t) are differentiable. This equation states that the optimum trajectory satisfies
This solution can be further simplified if f [p, p′, t] is independent of explicit dependence on t, i.e. the partial derivative of f [ ] with respect to t is 0 (i.e. δf/δt=0), then the condition may be simplified to the Beltrami identity: f [p, p′, t]−p′δf/δp′=C, where C is a constant of integration.
(iii) Minimizing the sum of squared intensity
The function f [ ] required to minimize the sum of squared intensity is as follows:
where p′ is the derivative of p with respect to t, and f [p, p′, t]=p′2[0·5p(1−p)]−1, representing the square of the selection intensity at time t. Applying the method of calculus of variation (Weisstein, Reference Weisstein2005) to the sum of squared intensities gives the following result: f [p, p′, t]−p′δf/δp′=−p′2[0·5p(1−p)]−1=C and p must satisfy
Solving this differential equation gives sin−1(1−2p)=At+B or, equivalently, p(t)=½[1−sin(At+B)], where A and B are constants of integration. This comes from noting that [p(1−p)]1/2=½[1−u 2]1/2, where u=(1−2p) converts the function into a recognizable standard integral form. A and B are determined by the desired change from t=0, …, T and have units of radians (not degrees). The optimal trajectory for minimizing the sum of squared intensity applied to the allele is therefore a segment of a sine wave.
(iv) Equalizing selection intensities
The objective function of equalizing the selection intensities is equivalent to making the selection intensity constant, i.e. p′[0·5p(1−p)]−1/2=C, which is the same differential equation as that obtained above for the criterion of minimizing the sum of squared intensities (eqn (A4)).
Appendix B
The error associated with minimizing the sum of squared intensity (as a percentage to the total) can be simplified as
given (δ(i t))2 can be neglected, which is twice the error of minimizing the total intensity (δ(i t)/i t).
Appendix C
This study considers the total intensity required to move from p 0 to p T, as
Note that in Goddard (Reference Goddard2009) ![]() and
and
Therefore, the increment in z is the accumulated selection intensity applied to the locus.
Appendix D
For large N, the total intensity for the continuous solution ![]() , while the total intensity for the discontinuous solution approaches
, while the total intensity for the discontinuous solution approaches ![]() . This is obtained by calculating separately the intensity from p 0 (assumed<0·5) to 0·5 and the intensity from 0·5 to 1. The first of these is
. This is obtained by calculating separately the intensity from p 0 (assumed<0·5) to 0·5 and the intensity from 0·5 to 1. The first of these is ![]() , which tends to
, which tends to ![]() as N becomes large, while the second is
as N becomes large, while the second is ![]() , giving a minimum of
, giving a minimum of ![]() for large N.
for large N.
Hence, for a continuous solution the sum of squared intensities ![]() and for a discontinuous solution
and for a discontinuous solution ![]() .
.
The sums of squared intensities from the two solutions for a range of T values are summarized below. When T=7, the two solutions yield roughly equal results, and for T>7, the continuous solution performs better than the discontinuous solution.