Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Agarwal, R. P.
1963.
Some further properties of a q-analogue of MacRobert's E-function.
Proceedings of the Glasgow Mathematical Association,
Vol. 6,
Issue. 1,
p.
34.

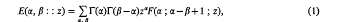
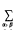 denotes that to the expression following it, a similar expression with α and β interchanged is to be added. For (1) he also gave the integral representation
denotes that to the expression following it, a similar expression with α and β interchanged is to be added. For (1) he also gave the integral representation