Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-29T14:38:36.105Z Has data issue: false hasContentIssue false
  • English
  • Français

A concavity problem in number theory

Published online by Cambridge University Press:  18 May 2009

Ian Anderson
Ian Anderson
Affiliation:
University of Glasgow
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For any fixed value of x, let 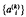denote the set of all positive integers with exactly k prime factors counted according to multiplicity, each prime factor being ≦ x. In an earlier paper [1] in this journal we posed the following problem. Let

Show the existence or non-existence of an integer K such that, if

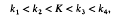
then

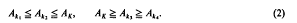
We now show that such a K exists, and that in (2) there is strict inequality in each case.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 12 , Issue 1 , April 1971 , pp. 10 - 11
Copyright
Copyright © Glasgow Mathematical Journal Trust 1971

References

REFERENCES

1.Anderson, I., Primitive sequences whose elements have no large prime factors, Glasgow Math. J. 10 (1969), 10–15.CrossRefGoogle Scholar
2.Anderson, I., On the divisors of a number, J. London Math. Soc. 43 (1968), 410–418.CrossRefGoogle Scholar
3.Lieb, E. H., Concavity properties and a generating function for Stirling numbers, J. Combinatorial Tlieory, 5 (1968), 203–206.CrossRefGoogle Scholar