Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Morikawa, Minoru
1963.
Calculation of Axially Symmetric Electrostatic Fields for Two Coaxial Equidiameter Cylinders.
Journal of Applied Physics,
Vol. 34,
Issue. 11,
p.
3179.
Tranter, C. J.
1963.
A Note on Dual Equations With Trigonometrical Kernels.
Proceedings of the Edinburgh Mathematical Society,
Vol. 13,
Issue. 3,
p.
267.

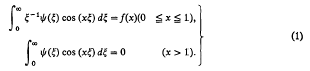
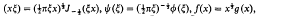 we obtain a pair of dual integral equations of the Titchmarsh type [1, p. 334] with α = − 1,
we obtain a pair of dual integral equations of the Titchmarsh type [1, p. 334] with α = − 1, 