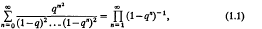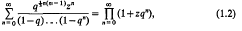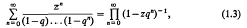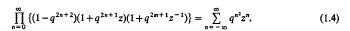Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Andrews, G. E.
1974.
A Pair of Theta Function Identities (L. Carlitz).
SIAM Review,
Vol. 16,
Issue. 4,
p.
553.
Andrews, George E.
1986.
Questions and Conjectures in Partition Theory.
The American Mathematical Monthly,
Vol. 93,
Issue. 9,
p.
708.
Andrews, George E
and
Garvan, F.G
1989.
Ramanujan's “Lost” Notebook VI: The mock theta conjectures.
Advances in Mathematics,
Vol. 73,
Issue. 2,
p.
242.
Andrews, G. E.
Bessenrodt, C.
and
Olsson, J. B.
1996.
A refinement of a partition identity and blocks of some modular characters.
Archiv der Mathematik,
Vol. 66,
Issue. 2,
p.
101.
Alladi, Krishnaswami
1999.
Topics in Number Theory.
p.
101.
Andrews, George E.
Knopfmacher, Arnold
Paule, Peter
and
Zimmermann, Burkhard
2001.
Symbolic Computation, Number Theory, Special Functions, Physics and Combinatorics.
Vol. 4,
Issue. ,
p.
33.
Pak, Igor
2006.
Partition bijections, a survey.
The Ramanujan Journal,
Vol. 12,
Issue. 1,
p.
5.
Rowell, Michael
and
Yee, Ae Ja
2009.
The Finite Heine Transformation and Conjugate Durfee Squares.
Integers,
Vol. 9,
Issue. 6,
Kim, Byungchan
2009.
A short note on the overpartition function.
Discrete Mathematics,
Vol. 309,
Issue. 8,
p.
2528.
Patkowski, Alexander E.
2010.
A note on the rank parity function.
Discrete Mathematics,
Vol. 310,
Issue. 4,
p.
961.
Berndt, Bruce C.
Kim, Byungchan
and
Yee, Ae Ja
2010.
Ramanujan's lost notebook: Combinatorial proofs of identities associated with Heine's transformation or partial theta functions.
Journal of Combinatorial Theory, Series A,
Vol. 117,
Issue. 7,
p.
957.
Brietzke, Eduardo H. M.
Santos, José Plínio O.
and
da Silva, Robson
2010.
Bijective proofs using two-line matrix representations for partitions.
The Ramanujan Journal,
Vol. 23,
Issue. 1-3,
p.
265.
Fang, Jian-Ping
2010.
SOME APPLICATIONS OF q-DIFFERENTIAL OPERATOR.
Journal of the Korean Mathematical Society,
Vol. 47,
Issue. 2,
p.
223.
Chen, Sandy H. L.
Chen, William Y. C.
Fu, Amy M.
and
Zang, Wenston J. T.
2011.
The Algorithm Z and Ramanujan’s 1 ψ 1 summation.
The Ramanujan Journal,
Vol. 25,
Issue. 1,
p.
37.
SANTOS, JOSE PLÍNIO O.
and
DA SILVA, ROBSON
2011.
ON A COMBINATORIAL PROOF FOR AN IDENTITY INVOLVING THE TRIANGULAR NUMBERS.
Bulletin of the Australian Mathematical Society,
Vol. 83,
Issue. 1,
p.
46.
Merca, Mircea
2012.
Fast Algorithm for Generating Ascending Compositions.
Journal of Mathematical Modelling and Algorithms,
Vol. 11,
Issue. 1,
p.
89.
Brietzke, Eduardo H. M.
Santos, José Plínio O.
and
da Silva, Robson
2013.
Combinatory Analysis.
Vol. 32,
Issue. ,
p.
263.
Alladi, Krishnaswami
2013.
Variants of classical q-hypergeometric identities and partition implications.
The Ramanujan Journal,
Vol. 31,
Issue. 1-2,
p.
213.
Andrews, George E.
Dixit, Atul
and
Yee, Ae Ja
2015.
Partitions associated with the Ramanujan/Watson mock theta functions ω(q), ν(q)and ϕ(q).
Research in Number Theory,
Vol. 1,
Issue. 1,
RatanBhattacharjee, Nil
and
Das, Sabuj
2015.
DEVELOPMENT OF LOVEJOY AND OSBURN’SOVERPARTITION FUNCTIONS.
International Journal of Research -GRANTHAALAYAH,
Vol. 3,
Issue. 1,
p.
41.