No CrossRef data available.
Article contents
Further Duals of a verbal Subgroup
Published online by Cambridge University Press: 18 May 2009
Extract
In a previous paper [3] we gave two methods for constructing subgroups which in certain senses may be considered to be dual to a verbal subgroup Vf(G) of an arbitrary group G. Associated with a word h (u, v) in the two symbols u and v, we have (i) the first dual subgroup 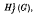 which is defined as the minimal subgroup of G containing all elements ξ of G for which
which is defined as the minimal subgroup of G containing all elements ξ of G for which
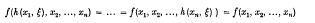
for all values of x1, x2, …, in xn in G, and (ii), the second dual subgroup 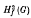 which is defined as the minimal subgroup of G containing all elements z of G for which
which is defined as the minimal subgroup of G containing all elements z of G for which
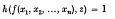
for all values of x1, x2, …, xn in G. Below we introduce slight variations to these definitions, which give rise to the concepts of the third and the fourth dual subgroups respectively. For certain values of h(u, v) we obtain concepts which also arise from 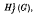 and
and 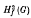 , namely, the marginal subgroup, the invariable subgroup and the centralizer of a verbal subgroup. We also obtain the new concepts of elemental subgroups and commutal subgroups and briefly sketch some of their properties. Finally we conclude by showing that MacLane's dual for the centralizer of a verbal subgroup is a closely related verbal subgroup.
, namely, the marginal subgroup, the invariable subgroup and the centralizer of a verbal subgroup. We also obtain the new concepts of elemental subgroups and commutal subgroups and briefly sketch some of their properties. Finally we conclude by showing that MacLane's dual for the centralizer of a verbal subgroup is a closely related verbal subgroup.
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 1959




