Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-25T17:20:40.385Z Has data issue: false hasContentIssue false
  • English
  • Français

ISOMETRIES AND DISCRETE ISOMETRY SUBGROUPS OF HYPERBOLIC SPACES

Published online by Cambridge University Press:  01 January 2009

XI FU  and
XIANTAO WANG
XI FU
Affiliation:
Department of Mathematics, Hunan Normal University, Changsha, Hunan 410081, People's Republic of China
XIANTAO WANG*
Affiliation:
Department of Mathematics, Hunan Normal University, Changsha, Hunan 410081, People's Republic of China e-mail: xtwang@hunnu.edu.cn
*
*Corresponding author.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 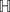n be the n-dimensional hyperbolic space with n ≥ 2. Suppose that G is a discrete, sense-preserving subgroup of Isom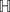n, the isometry group of 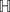n. Let p be the projection map from 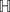n to the quotient space M = 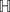n/G. The first goal of this paper is to prove that for any a ∈ ∂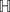n (the sphere at infinity of 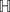n), there exists an open neighbourhood U of a i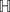n n ∪ ∂ 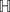n such that p is an isometry on U ∩ 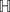n if and only if a ∈ oΩ(G) (the domain of proper discontinuity of G). This is a generalization of the main result discussed in the work by Y. D. Kim (A theorem on discrete, torsion free subgroups of Isom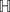n, Geometriae Dedicata109 (2004), 51–57). The second goal is to obtain a new characterization for the elements of Isom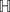n by using a class of hyperbolic geometric objects: hyperbolic isosceles right triangles. The proof is based on a geometric approach.

Keywords

Primary: 30F3551M10Secondary: 20H1022E40
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 51 , Issue 1 , January 2009 , pp. 31 - 38
Copyright
Copyright © Glasgow Mathematical Journal Trust 2008

References

REFERENCES

1.Ahlfors, L. V., Möbius transformations and Clifford numbers, in Differential geometry and complex analysis (Chavel, I. and Farkas, H. M., Editors) (Springer-Verlag, Berlin, 1985), 65–73.CrossRefGoogle Scholar
2.Ahlfors, L. V., On the fixed points of Möbius transformations in Rn, Ann. Acad. Sci. Fen. Ser. A. I. Math. 10 (1985), 15–27.CrossRefGoogle Scholar
3.Beardon, A. F., The geometry of discrete groups, Graduate text in mathematics, vol. 91 (Springer-Verlag, New York, 1983).Google Scholar
4.Gehring, F. W. and Martin, G. J., Discrete quasiconformal groups, Proc. Lond. Math. Soc. 55 (1987), 331–385.CrossRefGoogle Scholar
5.Jeffers, J., Lost theorems of geometry, Am. Math. Monthly 107 (2000), 800–812.CrossRefGoogle Scholar
6.Kim, Y. D., A theorem on discrete, torsion free subgroups of Isomℍn, Geom. Dedicata 109 (2004), 51–57.CrossRefGoogle Scholar
7.Li, B. and Wang, Y., Transformations and non-degenerate maps, Sci. China 48 (2005), 195–205.CrossRefGoogle Scholar
8.Li, B. amd Yao, G., On characterizations of sphere-preserving maps, Mathematical Proceedings of Cambridge Philosophical Society, to appear.Google Scholar
9.Maskit, B., Kleinian groups (Springer-Verlag, New York, 1988).Google Scholar
10.Ratcliffe, J. G., Foundations of hyperbolic manifolds, Graduate text in mathematics, Vol. 149 (Springer-Verlag, New York, 1994).Google Scholar
11.Tukia, P., Differentiability and rigidity of Möbius groups, Invent. Math. 2 (1985), 557–578.CrossRefGoogle Scholar
12.Wang, X. and Li, L., Algebraic convergence theorems of n-dimensional Kleinian groups, Israel J. Math. 162 (2007), 221–233.CrossRefGoogle Scholar
13.Wang, X., Li, L. and Cao, W., Discreteness criteria for Möbius groups acting on Rn, Israel J. Math. 150 (2005), 357–368.CrossRefGoogle Scholar
14.Wang, X. and Yang, W., Discreteness criteria of Möbius groups of high dimensions and convergence theorem of Kleinian groups, Adv. Math. 159 (2001), 68–82.CrossRefGoogle Scholar
15.Waterman, P. L., Purely elliptic Möbius groups, in Holomorphic functions and moduli, vol. II (Springer, New York, 1983), 173–178.Google Scholar
16.Waterman, P., Möbius transformations in several dimensions, Adv. Math. 101 (1993), 87–113.CrossRefGoogle Scholar