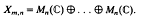Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Skowroński, A.
and
Weyman, J.
2000.
The algebras of semi-invariants of quivers.
Transformation Groups,
Vol. 5,
Issue. 4,
p.
361.
Domokos, M.
Kuzmin, S.G.
and
Zubkov, A.N.
2002.
Rings of matrix invariants in positive characteristic.
Journal of Pure and Applied Algebra,
Vol. 176,
Issue. 1,
p.
61.
Domokos, M
2003.
Polynomial Identities And Combinatorial Methods.
Kuz’min, S.G.
and
Zubkov, A.N.
2003.
Rings of invariants of 2×2 matrices in positive characteristic.
Linear Algebra and its Applications,
Vol. 365,
Issue. ,
p.
271.
Bocklandt, Raf
2005.
Quiver Quotient Varieties and Complete Intersections.
Algebras and Representation Theory,
Vol. 8,
Issue. 1,
p.
127.
DOMOKOS, MÁTYÁS
2011.
ON SINGULARITIES OF QUIVER MODULI.
Glasgow Mathematical Journal,
Vol. 53,
Issue. 1,
p.
131.
Florentino, Carlos
and
Lawton, Sean
2012.
Singularities of free group character varieties.
Pacific Journal of Mathematics,
Vol. 260,
Issue. 1,
p.
149.
Lawton, Sean
and
Manon, Christopher
2016.
Character varieties of free groups are Gorenstein but not always factorial.
Journal of Algebra,
Vol. 456,
Issue. ,
p.
278.