Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kirchberg, Eberhard
and
Vaillant, Ghislain
1992.
OnC *-algebras having linear, polynomial and subexponential growth.
Inventiones Mathematicae,
Vol. 108,
Issue. 1,
p.
635.
Samet-Vaillant, A.Y.
2000.
Free *-subalgebras of C*-algebras.
Journal of Functional Analysis,
Vol. 171,
Issue. 2,
p.
432.
Junge, M
Nielsen, N.J
Ruan, Zhong-Jin
and
Xu, Q
2004.
COLp spaces—the local structure of non-commutative Lp spaces.
Advances in Mathematics,
Vol. 187,
Issue. 2,
p.
257.

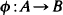 between C*-algebras, we define the multiplicity map
between C*-algebras, we define the multiplicity map 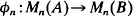 by
by 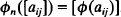 A linear map Ø is said to be
A linear map Ø is said to be 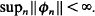 Let
Let 