Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ouyang, Lunqun
2011.
On Weak Annihilator Ideals of Skew Monoid Rings.
Communications in Algebra,
Vol. 39,
Issue. 11,
p.
4259.
Majidinya, A.
and
Moussavi, A.
2014.
Principally Quasi-Baer skew Generalized Power Series modules.
Communications in Algebra,
Vol. 42,
Issue. 4,
p.
1460.
Mazurek, Ryszard
2015.
Left principally quasi-Baer and left APP-rings of skew generalized power series.
Journal of Algebra and Its Applications,
Vol. 14,
Issue. 03,
p.
1550038.
Nasr-Isfahani, A. R.
2017.
Left APP differential polynomial rings.
Communications in Algebra,
Vol. 45,
Issue. 6,
p.
2444.

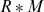 (induced by φ) to be left APP (left principally quasi-Baer, quasi-Baer, respectively).
(induced by φ) to be left APP (left principally quasi-Baer, quasi-Baer, respectively).