Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-02-11T11:51:09.276Z Has data issue: false hasContentIssue false
  • English
  • Français

Residuation theory and matrix multiplication on orthomodular lattices

Published online by Cambridge University Press:  18 May 2009

J. H. Bevis  and
C. K. Martin
J. H. Bevis
Affiliation:
Virginia Polytechnic Institute, Blacksburg, Virginia
C. K. Martin
Affiliation:
Virginia Polytechnic Institute, Blacksburg, Virginia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we consider mappings induced by matrix multiplication which are defined on lattices of matrices whose coordinates come from a fixed orthomodular lattice L (i.e. a lattice with an orthocomplementation denoted by ′ in which a ≦ b ⇒ a ∨ (a′ ∧ b) = b). 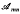will denote the set of all m × n matrices over L with partial order and lattice operations defined coordinatewise. For conformal matrices A and B the (i,j)th coordinate of the matrix product AB is defined to be (AB)ij = Vk(Aik ∧ BkJ). We assume familiarity with the notation and results of [1]. 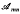is an orthomodular lattice and the (lattice) centre of 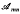is defined as 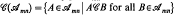, where we say that A commutes with B and write 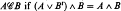. In § 1 it is shown that mappings from 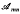into 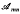characterized by right multiplication X → XP (P ∈ 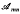) are residuated if and only if p ∈ ℘ (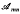). (Similarly for left multiplication.) This result is used to show the existence of residuated pairs. Hence, in § 2 we are able to extend a result of Blyth [3] which relates invertible and cancellable matrices (see Theorem 3 and its corollaries). Finally, for right (left) multiplication mappings, characterizations are given in § 3 for closure operators, quantifiers, range closed mappings, and Sasaki projections.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 10 , Issue 1 , January 1969 , pp. 60 - 65
Copyright
Copyright © Glasgow Mathematical Journal Trust 1969

References

REFERENCES

1.Bevis, J. H., Matrices over orthomodular lattices, Glasgow Math. J. 10 (1968), 55–59.CrossRefGoogle Scholar
2.Birkhoff, G., Lattice theory, Amer. Math. Soc. Colloquium Publications, Vol. 25, rev. ed. (New York, 1948).Google Scholar
3.Blyth, T. S., Residuation theory and Boolean matrices, Proc. Glasgow Math. Assoc. 6 (1964), 185–190.Google Scholar
4.Croisot, R., Applications residuées, Ann. Sci. Ecole Norm. Sup. (3) 73 (1956), 453–474.Google Scholar
5.Foulis, D. J., Baer *-semigroups, Proc. Amer. Math. Soc. 11 (1960), 648–654.Google Scholar
6.Foulis, D. J., Conditions for the modularity of an orthomodular lattice, Pacific J. Math. 11 (1961), 889–895.CrossRefGoogle Scholar
7.Janowitz, M. F., Quantifiers and orthomodular lattices, Pacific J. Math. 13 (1963), 1241–1249.CrossRefGoogle Scholar
8.Janowitz, M. F., A semigroup approach to lattices, Canad.J. Math. 18 (1966), 1212–1223.CrossRefGoogle Scholar
9.Molinaro, I., Demi-groupes résidutifs, J. Math. Pures Appl. 39 (1960), 319–356.Google Scholar
10.Rutherford, D. E., Inverses of Boolean matrices, Proc. Glasgow Math. Assoc. 6 (1963), 49–53Google Scholar