Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-15T10:18:22.000Z Has data issue: false hasContentIssue false
  • English
  • Français

Separability of the L1-space of a vector measure

Published online by Cambridge University Press:  18 May 2009

Werner J. Ricker
Werner J. Ricker
Affiliation:
School of Mathematics, University of New South Wales, Kensington 2033, Australia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let Σ be a σ-algebra of subsets of some set Ω and let μ:Σ→[0,∞] be a σ-additive measure. If Σ(μ) denotes the set of all elements of Σ with finite μ-measure (where sets equal μ-a.e. are identified in the usual way), then a metric d can be defined in Σ(μ) by the formula

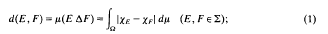
here E ΔF = (E\F) ∪ (F\E) denotes the symmetric difference of E and F. The measure μ is called separable whenever the metric space (Σ(μ), d) is separable. It is a classical result that μ is separable if and only if the Banach space L1(μ), is separable [8, p.137]. To exhibit non-separable measures is not a problem; see [8, p. 70], for example. If Σ happens to be the σ-algebra of μ-measurable sets constructed (via outer-measure μ*) by extending μ defined originally on merely a semi-ring of sets Γ ⊆ Σ, then it is also classical that the countability of Γ guarantees the separability of μ and hence, also of L1(μ), [8, p. 69].

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 34 , Issue 1 , January 1992 , pp. 1 - 9
Copyright
Copyright © Glasgow Mathematical Journal Trust 1992

References

REFERENCES

1.Bade, W. G., On Boolean algebras of projections and algebras of operators, Trans. Amer. Math. Soc. 80 (1955), 345–359.CrossRefGoogle Scholar
2.Dodds, P. G. and Ricker, W., Spectral measures and the Bade reflexivity theorem, J. Functional Analysis 61 (1985), 136–163.CrossRefGoogle Scholar
3.Dunford, N. and Schwartz, J. T., Linear operators I, 2nd Printing (Interscience, New York, 1964).Google Scholar
4.Hewitt, E. and Stromberg, K., Real and abstract analysis, Graduate Texts in Math., Vol. 25 (3rd Edition) (Springer–Verlag, 1975).Google Scholar
5.Kluvánek, I., The extension and closure of vector measures, in Vector and operator-valued measures and applications, pp. 175–189 (Academic Press, 1973).CrossRefGoogle Scholar
6.Kluvánek, I. and Knowles, G., Vector measures and control systems (North Holland, Amsterdam, 1976).Google Scholar
7.Ricker, W., Criteria for closedness of vector measures, Proc. Amer. Math. Soc. 91 (1984), 75–80.CrossRefGoogle Scholar
8.Zaanen, A. C., Integration (North Holland, Amsterdam, 1967).Google Scholar