Hostname: page-component-848d4c4894-pftt2 Total loading time: 0 Render date: 2024-06-07T16:38:36.540Z Has data issue: false hasContentIssue false
  • English
  • Français

Some remarks on the p-homotopy type of B∑p2

Published online by Cambridge University Press:  18 May 2009

Maurizio Brunetti
Maurizio Brunetti
Affiliation:
Dipartimento di Matematica e Applicazioni, Università di Napoli, Complesso Universitario Monte S. Angelo-Edificio t., via Cinta I-80126 Napoli, Italy
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G be a finite group, H a copy of its p-Sylow subgroup, and N the normalizer of H in G. A theorem by Nishida [10] states the p-homotopy equivalence of suitable suspensions of BN and BG when H is abelian. Recently, in [3] the authors proved a stronger result: let ΩkH be the subgroup of H generated by elements of order pk or less; if

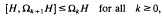
then BN and BG are stably p-homotopy equivalent. The hypothesis above is obviously verified when H is abelian. In the same paper the authors recall that H does not verify such condition when p = 2 and G = SL2(Fq) for a suitable odd prime power q; in this case BG and BN are not stably 2-homotopy equivalent.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 38 , Issue 3 , September 1996 , pp. 337 - 342
Copyright
Copyright © Glasgow Mathematical Journal Trust 1996

References

REFERENCES

1.Benson, D. J. and Feshbach, M., Stable splittings of classifying spaces of finite groups. Topology 31 (1993), 157–176.CrossRefGoogle Scholar
2.Brunetti, M., A family of 2(p - l)-sparse cohomology theories and some actions on h*(BC pn), Math. Proc. Camb. Phil. Soc. 116 (1994), 223–228.CrossRefGoogle Scholar
3.Henn, H.-W. and Priddy, S., p-nilpotence, classifying space indecomposability, and other properties of almost all finite groups, Comment. Math. Helvetica 69 (1993), 335–350.CrossRefGoogle Scholar
4.Hopkins, M. J., Kuhn, N. J. and Ravenel, D. C., Morava K-theories of classifying spaces and generalized characters for finite groups, in Algebraic Topology (San Feliu de Guixols, 1990), Lecture Notes in Mathematics No 1509 (Springer-Verlag, 1992), 186–209.Google Scholar
5.Hunton, J. R., The Morava K-theories of wreath products, Math. Proc. Camb. Phil. Soc. 107 (1990), 309–318.CrossRefGoogle Scholar
6.Kuhn, N. J., The mod p K-theory of classifying spaces of finite groups, J. Pure Appl. Alg. 44 (1987), 269–271,CrossRefGoogle Scholar
7.Martino, J. and Priddy, S., The complete stable splitting for the classifying space of a finite group, Topology 31 (1992), 143–156.CrossRefGoogle Scholar
8.Mitchell, S. and Priddy, S., Symmetric product spectra and splitting of classifying spaces, Amer. J. Math. 106 (1984), 219–232.CrossRefGoogle Scholar
9.Neumann, P. M., On the structure of standard wreath products of groups, Math. Z. 84 (1964), 343–373.CrossRefGoogle Scholar
10.Nishida, G., Stable homotopy type of classifying spaces of finite groups, in Algebraic and topological theories (Kinokuniya, Tokyo, 1986), 391–404.Google Scholar