Hostname: page-component-848d4c4894-m9kch Total loading time: 0 Render date: 2024-06-08T02:24:15.873Z Has data issue: false hasContentIssue false
  • English
  • Français

Spectra of conjugated ideals in group algebras of abelian groups of finite rank and control theorems

Published online by Cambridge University Press:  18 May 2009

Anatolii V. Tushev
Anatolii V. Tushev
Affiliation:
Department of Mathematics, University of Dnepropetrovsk, Prospect Gagarina 72, Dnepropetrovsk, 320625, Ukraine
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Throughout kwill denote a field. If a group Γ acts on aset A we say an element is Γ-orbital if its orbit is finite and write ΔΓ(A) for the subset of such elements. Let I be anideal of a group algebra kA; we denote by I+ the normal subgrou(I+1)∩A of A. A subgroup B of an abelian torsion-free group A is said to be dense in A if A/B is a torsion-group. Let I be an ideal of a commutative ring K; then the spectrum Sp(I) of I is the set of all prime ideals P of K such that I≤P. If R is a ring, M is an R-module and x ɛ M we denote by 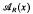the annihilator of x in R. We recall that a group Γ is said to have finite torsion-free rank if it has a finite series in which each factoris either infinite cyclic or locally finite; its torsion-free rank r0(Γ) is then defined to be the number of infinite cyclic factors in such a series.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 38 , Issue 3 , September 1996 , pp. 309 - 320
Copyright
Copyright © Glasgow Mathematical Journal Trust 1996

References

REFERENCES

1.Brookes, C. J. B., Ideals in group rings of soluble groups of finite rank, Math. Proc. Camb. Phil. Soc. 97 (1985), 27–49.CrossRefGoogle Scholar
2.Brookes, C. J. B. and Brown, K. A., Primitive group rings and Noetherian rings of quotients. Trans. Amer. Math. Soc. 288 (1985), 605–623.CrossRefGoogle Scholar
3.Brookes, C. J. B. and Brown, K. A., Injective modules, induction maps and endomorphism rings. Proc. London Math. Soc. (3) 67 (1993), 127–158.CrossRefGoogle Scholar
4.Brown, K. A., The Nullstellensatz for certain group algebras. J. London Math. Soc. 26 (1982) 425–434.CrossRefGoogle Scholar
5.Hall, P., Finiteness conditions for soluble groups. Proc. London Math. Soc. 4 (1954) 419–436.Google Scholar
6.Hall, P., On the finiteness of certain soluble groups. Proc. London Math. Soc. 9 (1959) 595–622.CrossRefGoogle Scholar
7.Harper, D. L., Primitive irreducible representation of nilpotent groups. Math. Proc. Camb. Phil. Soc. 82 (1977), 241–247.CrossRefGoogle Scholar
8.Harper, D. L., Primitivity in representations of polycyclic groups. Math. Proc. Camb. Phil. Soc. 88 (1980), 15–31.CrossRefGoogle Scholar
9.Hartley, B., A dual approach to Cernikov modules. Math. Proc. Camb. Math. Soc. 82 (1977), 215–239.CrossRefGoogle Scholar
10.Musson, I. M., Representations of infinite soluble groups. Glasgow Math. J. 24 (1983), 43–52CrossRefGoogle Scholar
11.Musson, I. M., Irreducible modules for polycyclic groupalgebras. Canad. J. Math. 33 (1981), 901–914.CrossRefGoogle Scholar
12.Nabney, I. T., Soluble minimax groups and their representations. Ph.D. thesis (University of Cambridge, 1989).Google Scholar
13.Passman, D. S., Infinite crossed products (Academic Press, Boston, 1989).Google Scholar
14.Roseblade, J. E., Group rings of polycyclic groups, J. Pure Appl. Algebra. 3 (1973) 307–328.CrossRefGoogle Scholar
15.Segal, D., Irreducible representations of finitely generated nilpotent groups, Math. Proc. Camb. Phil. Soc. 81 (1977), 201–208.CrossRefGoogle Scholar
16.Wehrfritz, B. A. F., Infinite linear groups (Springer-Verlag, 1973).CrossRefGoogle Scholar
17.Wehrfritz, B. A. F., Invariant maximal ideals in certain group algebras. J. London Math. Soc. 46 (1992),101–110.CrossRefGoogle Scholar
18.Wilson, J. S., Soluble products of minimax groups, and nearly surjective derivations. J. Pure and Appl. Algebra. 53 (1988), 297–318.CrossRefGoogle Scholar