No CrossRef data available.
Article contents
STABLE PROPERTIES OF HYPERRELEXIVITY
Published online by Cambridge University Press: 21 July 2015
Abstract
Recently, a new equivalence relation between weak* closed operator spaces acting on Hilbert spaces has appeared. Two weak* closed operator spaces 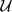 ${\mathcal{U}}$,
${\mathcal{U}}$, 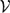 ${\mathcal{V}}$ are called weak TRO equivalent if there exist ternary rings of operators
${\mathcal{V}}$ are called weak TRO equivalent if there exist ternary rings of operators 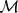 ${\mathcal{M}}$i, i = 1, 2 such that
${\mathcal{M}}$i, i = 1, 2 such that 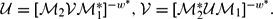 ${\mathcal{U}}=[{\mathcal{M}}_2{\mathcal{V}}{\mathcal{M}}_1^*]^{-w^*}, {\mathcal{V}}=[{\mathcal{M}}_2^*{\mathcal{U}}{\mathcal{M}}_1]^{-w^*}.$ Weak TRO equivalent spaces are stably isomorphic, and conversely, stably isomorphic dual operator spaces have normal completely isometric representations with weak TRO equivalent images. In this paper, we prove that if
${\mathcal{U}}=[{\mathcal{M}}_2{\mathcal{V}}{\mathcal{M}}_1^*]^{-w^*}, {\mathcal{V}}=[{\mathcal{M}}_2^*{\mathcal{U}}{\mathcal{M}}_1]^{-w^*}.$ Weak TRO equivalent spaces are stably isomorphic, and conversely, stably isomorphic dual operator spaces have normal completely isometric representations with weak TRO equivalent images. In this paper, we prove that if 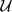 ${\mathcal{U}}$ and
${\mathcal{U}}$ and 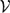 ${\mathcal{V}}$ are weak TRO equivalent operator spaces and the space of I × I matrices with entries in
${\mathcal{V}}$ are weak TRO equivalent operator spaces and the space of I × I matrices with entries in 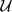 ${\mathcal{U}}$, MIw(
${\mathcal{U}}$, MIw(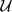 ${\mathcal{U}}$), is hyperreflexive for suitable infinite I, then so is MIw(
${\mathcal{U}}$), is hyperreflexive for suitable infinite I, then so is MIw(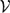 ${\mathcal{V}}$). We describe situations where if
${\mathcal{V}}$). We describe situations where if 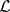 ${\mathcal{L}}$1,
${\mathcal{L}}$1, 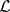 ${\mathcal{L}}$2 are isomorphic lattices, then the corresponding algebras Alg(
${\mathcal{L}}$2 are isomorphic lattices, then the corresponding algebras Alg(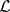 $\mathcal{L}$1), Alg(
$\mathcal{L}$1), Alg(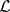 $\mathcal{L}$2) have the same complete hyperreflexivity constant.
$\mathcal{L}$2) have the same complete hyperreflexivity constant.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 2015

