Hostname: page-component-848d4c4894-nr4z6 Total loading time: 0 Render date: 2024-06-07T16:27:20.010Z Has data issue: false hasContentIssue false
  • English
  • Français

TOPOLOGICAL 4-MANIFOLDS WITH 4-DIMENSIONAL FUNDAMENTAL GROUP

Part of: Topological manifolds

Published online by Cambridge University Press:  23 July 2021

DANIEL KASPROWSKI  and
MARKUS LAND
DANIEL KASPROWSKI
Affiliation:
Rheinische Friedrich-Wilhelms-Universität Bonn, Mathematisches Institut, Endenicher Allee 60, 53115Bonn, Germany e-mail: kasprowski@uni-bonn.de
MARKUS LAND
Affiliation:
Department of Mathematical Sciences, University of Copenhagen, 2100Copenhagen, Denmark e-mail: markus.land@math.ku.dk
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 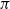$\pi$ be a group satisfying the Farrell–Jones conjecture and assume that $B\pi$ is a 4-dimensional Poincaré duality space. We consider topological, closed, connected manifolds with fundamental group 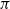$\pi$ whose canonical map to 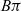$B\pi$ has degree 1, and show that two such manifolds are s-cobordant if and only if their equivariant intersection forms are isometric and they have the same Kirby–Siebenmann invariant. If 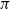$\pi$ is good in the sense of Freedman, it follows that two such manifolds are homeomorphic if and only if they are homotopy equivalent and have the same Kirby–Siebenmann invariant. This shows rigidity in many cases that lie between aspherical 4-manifolds, where rigidity is expected by Borel’s conjecture, and simply connected manifolds where rigidity is a consequence of Freedman’s classification results.

MSC classification

Secondary: 57N65: Algebraic topology of manifolds
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 64 , Issue 2 , May 2022 , pp. 454 - 461
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Cochran, T. D. and Habegger, N., On the homotopy theory of simply connected four manifolds, Topology 29(4) (1990), 419–440.CrossRefGoogle Scholar
Cavicchioli, A. and Hegenbarth, F., On the homotopy classification of 4-manifolds having the fundamental group of an aspherical 4-manifold, Osaka J. Math. 37(4) (2000), 859–871.Google Scholar
Freedman, M. H. and Quinn, F., Topology of 4-manifolds, Princeton Mathematical Series, vol. 39 (Princeton University Press, Princeton, NJ, 1990).Google Scholar
Freedman, M. H., The topology of four-dimensional manifolds, J. Differential Geom. 17(3) (1982), 357–453.CrossRefGoogle Scholar
Freedman, M. H. and Teichner, P., 4-manifold topology. I. Subexponential groups, Invent. Math. 122(3) (1995), 509–529.CrossRefGoogle Scholar
Hillman, J. A., ${\rm PD}_4$-complexes with strongly minimal models, Topology Appl. 153(14) (2006), 2413–2424.Google Scholar
Hambleton, I. and Kreck, M., Cancellation, elliptic surfaces and the topology of certain four- manifolds., J. Reine Angew. Math. 444 (1993), 79–100.Google Scholar
Hambleton, I., Kreck, M., and Teichner, P., Topological 4-manifolds with geometrically two-dimensional fundamental groups, J. Topol. Anal. 1(2) (2009), 123–151.Google Scholar
Khan, Q., Homotopy invariance of 4-manifold decompositions: connected sums, Topology Appl. 159(16) (2012), 3432–3444.CrossRefGoogle Scholar
Kreck, M. and LÜck, W., Topological rigidity for non-aspherical manifolds, Pure Appl. Math. Q. 5(3) (2009), Special Issue: In honor of Friedrich Hirzebruch. Part 2, 873–914.Google Scholar
Kasprowski, D., Land, M., Powell, M., and Teichner, P., Stable classification of 4-manifolds with 3-manifold fundamental groups, J. Topol. 10(3) (2017), 827–881.CrossRefGoogle Scholar
Krushkal, V. S. and Quinn, F., Subexponential groups in 4-manifold topology, Geom. Topol. 4 (2000), 407–430.Google Scholar
Kreck, M., Surgery and duality, Ann. Math. (2) 149(3) (1999), 707–754.CrossRefGoogle Scholar
Kirby, R. C. and Taylor, L. R., A survey of 4-manifolds through the eyes of surgery, Surveys on Surgery Theory, Vol. 2, Ann. of Math. Stud., vol. 149 (Princeton Univ. Press, Princeton, NJ, 2001), 387–421.Google Scholar
LÜck, W., Assembly maps, Handbook of Homotopy Theory; editor: Haynes Miller (CRC Press/Chapman and Hall, 2019).CrossRefGoogle Scholar
LÜck, W., Isomorphism conjectures in K- and L-theory, 2019, Available at https://www.him.uni-bonn.de/lueck/, ongoing book project.Google Scholar
Ranicki, A. A., Exact sequences in the algebraic theory of surgery, Mathematical Notes, vol. 26 (Princeton University Press, Princeton, N.J.; University of Tokyo Press, Tokyo, 1981).Google Scholar
Ranicki, A. A., Lower K- and L-theory, London Mathematical Society Lecture Note Series, vol. 178 (Cambridge University Press, Cambridge, 1992).Google Scholar
Ranicki, A. A., Algebraic L-theory and topological manifolds, Cambridge Tracts in Mathematics, vol. 102 (Cambridge University Press, Cambridge, 1992). MR 1211640 (94i:57051)Google Scholar
Shaneson, J. L., Wall’s surgery obstruction groups for $G\times Z$, Ann. Math. (2) 90 (1969), 296–334.CrossRefGoogle Scholar
Wall, C. T. C., Poincaré complexes. I, Ann. Math. (2) 86 (1967), 213–245.CrossRefGoogle Scholar