No CrossRef data available.
Article contents
Triangular matrix categories over quasi-hereditary categories
Published online by Cambridge University Press: 21 March 2024
Abstract
In this paper, we prove that the lower triangular matrix category 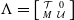 $\Lambda =\left [ \begin{smallmatrix} \mathcal{T}&0\\ M&\mathcal{U} \end{smallmatrix} \right ]$, where
$\Lambda =\left [ \begin{smallmatrix} \mathcal{T}&0\\ M&\mathcal{U} \end{smallmatrix} \right ]$, where 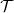 $\mathcal{T}$ and
$\mathcal{T}$ and 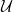 $\mathcal{U}$ are
$\mathcal{U}$ are 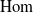 $\textrm{Hom}$-finite, Krull–Schmidt
$\textrm{Hom}$-finite, Krull–Schmidt 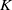 $K$-quasi-hereditary categories and
$K$-quasi-hereditary categories and 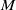 $M$ is an
$M$ is an 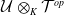 $\mathcal{U}\otimes _K \mathcal{T}^{op}$-module that satisfies suitable conditions, is quasi-hereditary. This result generalizes the work of B. Zhu in his study on triangular matrix algebras over quasi-hereditary algebras. Moreover, we obtain a characterization of the category of the
$\mathcal{U}\otimes _K \mathcal{T}^{op}$-module that satisfies suitable conditions, is quasi-hereditary. This result generalizes the work of B. Zhu in his study on triangular matrix algebras over quasi-hereditary algebras. Moreover, we obtain a characterization of the category of the 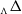 $_\Lambda \Delta$-filtered
$_\Lambda \Delta$-filtered 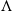 $\Lambda$-modules.
$\Lambda$-modules.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust
References
Assem, I., Simson, D. and Skowrónski, A., Elements of the representation theory of associative algebras 1: techniques of representation theory, london mathematical society student texts 65, London Mathematical Society Student Texts, vol. 65 (Cambridge University Press, Cambridge, 2006).CrossRefGoogle Scholar
Auslander, M., Representation theory of Artin algebras I, Comm. Algebra 3(1) (1974), 177–268.Google Scholar
Auslander, M., Platzeck, M. I. and Todorov, G., Homological theory of idempotent ideals, Trans. Am. Math. Soc. 332(2) (1992), 667–692.CrossRefGoogle Scholar
Auslander, M. and Reiten, I., Stable equivalence of dualizing R-varieties, Adv. Math. 12(3) (1974).CrossRefGoogle Scholar
Auslander, M., Reiten, I. and Smalø, S., Representation theory of artin algebras, Studies in Advanced Mathematics, vol. 36 (Cambridge University Press, 1995).CrossRefGoogle Scholar
Barot, M., Introduction to the representation theory of algebras (Springer, Cham, 2015). doi:10.1007/978-3-319-11475-0.CrossRefGoogle Scholar
Bautista, R., Liu, S. and Paquette, Ch., Representation theory of strongly locally finite quivers, Proc. London Math. Soc. 106(1) (2013), 97–162.CrossRefGoogle Scholar
Cline, E., Parshall, B. J. and Scott, L. L., Algebraic stratification in reprsentation categories, J. Algebra 117(2) (1988), 504–521.CrossRefGoogle Scholar
Dlab, V., Quasi-hereditary algebras, inFinite dimensional algebras (Springer-Verlag, 1993).Google Scholar
Dlab, V., Quasi-hereditary algebras revisited, An. St. Univ. Ovidius. Constanta 4 (1996), 43–54.Google Scholar
Dlab, V. and Ringel, C. M., Quasi-hereditary algebras, Illinois J. Math. 33(2) (1989), 280–291.CrossRefGoogle Scholar
Dlab, V. and Ringel, C. M., The module theoretical approach to quasi-hereditary algebras, in Representations of algebras and related topics, London Mathematical Society, vol. 168 (LNS, 1992), 200–224.CrossRefGoogle Scholar
Krause, H., Highest weight categories and recollements, Ann. de l’Institut Fourier 67(6) (2017), 2679–2701.CrossRefGoogle Scholar
Krause, H., Krull-Schmidt categories and projective covers, Expo. Math. 33(4) (4)2015), 535–549.CrossRefGoogle Scholar
Leszczyński, Z., On the representation type of tensor product algebras, Fund. Math. 144 (1994).CrossRefGoogle Scholar
León-Galeana, A., Ortíz-Morales, M. and Santiago, V., Triangular matrix categories II: recollements and functorially finite subcategories, Algebr. Represent. Theor. 26(3) (2023), 783–829. doi:10.1007/s10468-022-10113-w.CrossRefGoogle Scholar
León-Galeana, A., Ortíz-Morales, M. and Santiago, V., Triangular matrix categories I: dualizing varieties and generalized one-point extension, Algebr. Represent Theor. 26 (2023), 831–880. doi:10.1007/s10468-022-10114.CrossRefGoogle Scholar
Marcos, E., Mendoza, O., Sáenz, C. and Santiago, V., Standardly stratified lower triangular
 $\mathbb K$
-algebras with enough idempotents, J. Pure Appl. Algebra 227(5) (2023).CrossRefGoogle Scholar
$\mathbb K$
-algebras with enough idempotents, J. Pure Appl. Algebra 227(5) (2023).CrossRefGoogle Scholar
Martínez-Villa, R. and Ortíz-Morales, M., Tilting theory and functor categories II. Generalized Tilting, Appl. Categor. Struct. 21 (2013), 311–348.CrossRefGoogle Scholar
Martínez-Villa, R. and Ortíz-Morales, M., Tilting theory and functor categories I. Classical tilting, Appl. Categor. Struct. 22 (2014), 595–646.CrossRefGoogle Scholar
Mendoza, O., Ortiz, M., Saenz, C. and Santiago, V., A generalization of the theory of standarly stratified algebras: standardly stratified ringoids, Glasgow Math. J. (2020), 1–36.Google Scholar
Ortiz, M., The Auslander-Reiten components seen as quasi-hereditary categories, Appl. Categor. Struct. 26 (2018), 239–285.CrossRefGoogle Scholar
Parshall, B. J. and Scott, L. L., Derived categories, quasi-hereditary algebras and algebraic groups, in Algebra, Proceedings of the Workshop, Ottawa/Canada 1987, Math. Lect. Note Ser., Expo. Math., CRAF, Carleton Univ. 3, vol. 105 (1987).Google Scholar
Ringel, C. M., The category of modules with good filtrations over a quasi-hereditary algebra has almost split sequences, Math. Z. 208 (1991), 209–223.CrossRefGoogle Scholar
Rodríguez-Valdés, L. G., Sandoval-Miranda, M. L. S. and Santiago-Vargas, V., Homological theory of k-idempotent ideals in dualizing varieties, Commun. Algebra 50(5) (2022).CrossRefGoogle Scholar
Scott, L. L., Simulating algebraic geometry with algebra I: the algebraic theory of derived categories, in The Arcata Conference on Representations of Finite Groups (Arcata, Calif., 1986) Proceedings of Symposia in Pure Mathematics (AMS, 1987), 2,71–281.CrossRefGoogle Scholar
Zhu, B., Triangular matrix algebras over quasi-hereditary algebras, Tsukuba J. Math. 25(1) (2001), 1–11.CrossRefGoogle Scholar
Šťovíček, J., Telescope conjecture, idempotent ideals and the transfinite radical, Trans. Am. Math. Soc. 362(3) (2010), 1475–1489.CrossRefGoogle Scholar


