Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-24T20:13:17.554Z Has data issue: false hasContentIssue false
  • English
  • Français

Universal notions characterizing spectral decompositions

Published online by Cambridge University Press:  18 May 2009

Ridgley Lange  and
Shengwang Wang
Ridgley Lange
Affiliation:
Department of Mathematics, Hampton University, Hampton, Virginia 23668, U.S.A.
Shengwang Wang
Affiliation:
Department of Mathematics, Nanjing University, Nanjing, Jiangsu 210008, Peoples Republic of China
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this note we characterize certain types of spectral decomposition in terms of “universal” notions valid for any operator on a Banach space. To be precise, let X be a complex Banach space and let T be a bounded linear operator on X. If F is a closed set in the plane C, let X(T, F) consist of all y ∈ X satisfying thes identity

where f:C\F → X is analytic. It is then easy to see that X(T, F) is a T-invariant linear manifold in X. Moreover, if y ∈ X then

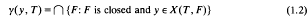
is a compact subset of the spectrum σ(T). Our aim is to give necessary and sufficient conditions for a decomposable or strongly decomposable operator in terms of X(T, F) and γ(y, T). Recall that T is decomposable if whenever G1G2 are open and cover C there exist T-invariant closed linear manifolds M1, M2 with X= M1 + M2 and σ(T | M1) ⊂ Gi(i = 1,2) (equivalently, σ(T | Mi)⊂ Ḡi, see [4, p. 57]). In this case, X(T, F) is norm closed if Fis closed and each y in X has a unique maximally defined local resolvent satisfying (1.1) on C\Fy; Fy is called the local spectrum σ(y, T) and coincides with γ(y, T). Hence T has the single valued extension property (SVEP); i.e., zero is the only analytic function f:V → X satisfying (z − T)f(z) = 0 on V. If T is decomposable and the restriction T | X(T, F) is also decomposable for each closed F, then T is called strongly decomposable. We point out that Albrecht [2] has shown by example that not every decomposable operator is strongly decomposable, while Eschmeier [6]has given a simpler construction to show that this phenomenon occurs even in Hilbert space.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 34 , Issue 1 , January 1992 , pp. 109 - 116
Copyright
Copyright © Glasgow Mathematical Journal Trust 1992

References

REFERENCES

1.Albrecht, E., An example of a C ∞ (C)-decomposable operator which is not C ∞ (C)-spectral, Rev. Roum. Math. Pures Appl. 19 (1974), 131–139.Google Scholar
2.Albrecht, E., On two questions of I. Colojoara and C. Foias, Manuscripta Math. 25 (1978), 1–15.CrossRefGoogle Scholar
3.Apostol, C., Restrictions and quotients of decomposable operators, Rev. Roum. Math. Pures Appl. 13 (1968), 147–150.Google Scholar
4.Colojoara, I. and Foias, C., Theory of generalized spectral operators (Gordon and Breach, New York, 1968).Google Scholar
5.Erdelyi, I. and Wang, S., A local spectral theory for closed operators, London Math. Soc. Lecture Notes No. 105 (Cambridge University Press, Cambridge, 1985).CrossRefGoogle Scholar
6.Eschmeier, J., A decomposable Hilbert space operator which is not strongly decomposable, Integral Equations Operator Theory 11 (1988), 161–172.CrossRefGoogle Scholar
7.Huang, S. W., On operator-characterization of decomposable operators, Southwestern Normal College Research Rep. 1, no. 1 (1985), 11–18.Google Scholar
8.Lange, R. and Wang, S., New criteria for a decomposable operator, Illinois J. Math. 31 (1987), 438–445.CrossRefGoogle Scholar
9.Taylor, A. E. and Lay, D. C., Introduction to functional analysis (Wiley, New York, 1980).Google Scholar
10.Wang, S., Theory of spectral decompositions with respect to the identity for closed operators, Chinese Ann. Math. Ser. B 6 (1985), 269–279.Google Scholar